基于改进TOPSIS的制造车间重调度决策方法研究

刘 壮，张中敏，杜先军

(合肥工业大学 机械与汽车工程学院，合肥 230009)

基于改进TOPSIS的制造车间重调度决策方法研究

刘 壮，张中敏，杜先军

(合肥工业大学 机械与汽车工程学院，合肥 230009)

针对制造车间最优重调度方案甄选问题，提出了一种基于改进逼近理想解排序的制造车间重调度决策方法。以可选调度方案集作为研究对象，考虑调度方案变更过程的耗损，设计工序相似性和额外机器能耗决策指标，实现调度方案性能的量化描述；利用基于Kullback-Leibler距离和灰色关联度的改进逼近理想解排序方法，确定可选调度方案间的偏序关系，以判断是否触发重调度及选取最优重调度方案。最后，通过实例验证了所建立重调度决策方法的合理性和有效性。

决策指标；改进逼近理想解排序；重调度决策方法

0 引言

现代制造车间在实际生产过程中经常面临各种扰动事件，如机器故障、紧急订单插入、操作延迟、工件返工或报废等。生产扰动的发生将导致原调度方案逐渐偏离实际生产情形，致使原调度方案有效性降低，甚至失去可行性。为保证生产系统持续稳定地运行，则需修正或重新生成调度方案，由此引出了制造车间重调度问题。重调度问题作为优化调度问题的延伸，已成为生产调度领域研究的热点，备受国内外学者的关注，如Vieira等[1]提出了制造车间的重调度研究体系；阎志华等[2]通过蜂群算法解决工件随机到达环境下的作业车间重调度问题；Akkan[3]为兼顾重调度的稳定性和鲁棒性，提出了分支定界与局部搜索结合的混合算法；文献[4-6]考虑频繁重调度易导致生产系统的振荡，以事件驱动策略为研究对象进行了一系列改进研究；乔非等[7]引入最小重调度时间间隔约束，避免混合驱动策略中出现重调度触发点间隔过小(或过大)现象，保证系统实时性和稳定性；Petrovic等[8]以生产持续时间和原材料缺货量为参数描述生产过程的不确定性，建立了基于模糊推理的重调度决策系统；刘明周等[9]提出基于损益云模型的重调度决策方法，实现重调度触发判定及调度方案的选取。

综上所述，现有重调度研究主要集中于重调度方法和重调度策略优化方面，而有关重调度决策研究相对较少。通过重调度决策能帮助管理者了解调度变更的性能优劣，避免因伪最优重调度方案而造成的损失，保证生产系统稳定运行。因此，本文在现有研究基础上，考虑重调度耗损，提出基于改进TOPSIS的重调度决策方法。首先，构建重调度决策模型，模型中以可选调度方案集为决策对象，设计的重调度决策指标作为方案评判标准，并采用G1法进行决策指标赋权；其次，采用基于Kullback-Leibler距离和灰色关联度的改进TOPSIS对可选调度方案排序，实现重调度触发判定及最优重调度方案选择；最后，通过实例论证决策方法合理性。

1 重调度决策问题描述

重调度决策问题主要包括决策对象的确立、决策指标的设计及指标的赋权，其中决策对象为可选调度方案集，由右移重调度方法和智能搜索方法生成的调度方案组成，具体表示为{F1,F2,…,FK}，F1表征采用右移重调度形成的调度方案。

1.1 决策指标

1.1.1 工序相似性指标

JobShop制造车间发生生产扰动后，为适应实时工况的变化，需要实施重调度。在重调度实施(即调度方案变更)过程中，由于车间生产制造资源的重新配置，致使可选调度方案与原调度方案出现偏离，产生一定附加成本，并可能造成工件完工时间的延迟。为降低重调度实施的损失，需要尽量避免车间各工件工序的加工机器、加工顺序及开始加工时间的调整，即尽量与原调度方案工序的安排相同。因此，构建工序相似性指标，表征可选调度方案与原调度方案相似程度：

(1)

(2)

式中，zij为调度决策变量，当zij为0时，表示可选调度方案和原调度方案中工件i的第j道工序的加工机器相同，当zij为1时，表示可选调度方案和原调度方案中工件i的第j道工序的加工机器不同。

1.1.2 额外机器能耗指标

随着人类社会环保意识的加强，制造企业越来越关注制造车间的节能减排。本文从加工机器低碳策略角度出发，对重调度实施过程的加工机器能源耗损进行分析。由于原调度方案是静态制造车间生产环境下经优化所获得的最满意调度方案即该调度方案性能水平最优，由此可知，在加工机器调度性能方面，生产扰动发生后重调度方法所形成的可选调度方案必然比原调度方案增加一定的加工机器空载运行时间，即造成一定的额外能源消耗。因此，构建额外机器能耗指标，表征调度方案变更过程中的能耗损失：

(3)

1.2 指标赋权

G1法是对AHP法的改进，无需进行一致性检验，克服了AHP法计算量大、计算复杂等缺点。方法通过专家对指标的重要性排序及相邻指标重要程度之比，确定各指标的权重w，参考文献[11]，指标赋权如下：

(1) 专家确定各指标的序关系：

I1≻I2≻…≻Il，l=1,2,…N

(4)

式中：Il为指标排序后的第l个指标。

(2) 依据专家知识经验，确定相邻指标的相对重要程度：

(5)

式中，zl为指标Il-1与指标Il的相对重要程度。

(3)计算指标的权重如下所示：

(6)

式中，wN表示指标IN的权重；wl-1表示指标Il-1的权重，wl表示指标Il的权重。

2 重调度决策方法

TOPSIS因具有计算简单、结果量化客观等优点，在决策问题解决上得到广泛应用。但传统TOPSIS只体现了评价对象与理想解的位置相似程度，当评价对象连线被正、负理想解连线垂直平分或评价对象位于正、负理想解连线中垂线上，则无法区分优劣[12]。而信息论中Kullback-Leibler距离能有效解决位于正、负理想解连线中垂线的评价对象排序问题[13]，同时灰色关联分析法能很好地评价曲线(评价对象的各指标构成)间形状相似性。因此，可在传统TOPSIS中将Kullback-Leibler距离与灰色关联度结合来替代欧式距离，使决策效果更加合理，基于改进TOPSIS的重调度决策方法步骤如下：

Step1:构建加权标准决策矩阵：

(7)

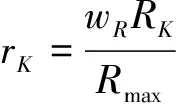
Step2: 由于决策指标越小越好，借鉴TOPSIS思想，确定正、负理想解：

(8)

Step3:考虑欧式距离表征可选调度方案与正、负理想解相似程度的局限性，本文将Kullback-Leibler距离和灰色关联度结合，构建综合相似度公式，具体计算如下所示：

(9)

(10)

式中，ε为分辨系数，通常取值为0.5。

(11)

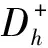
Step4:计算可选调度方案Fh的相对贴近度Ah为：

(12)

Step5:按照相对贴近度从大到小对可选调度方案排序，并进行序列分析：

(13)

Step6:若重调度方案集φR为∅，则继续执行原调度方案，反之，则触发重调度，并选择相对贴近度最大的调度方案作为最优重调度方案。

3 实例验证

本文以Benchmark6×6JobShop调度问题为例，通过Matlab7.8编写的仿真程序分析决策方法的可行性。假设t=25时，1号机器发生故障，维修5min。采用混合粒子群优化算法[14]生成调度方案，并与右移调度方案构成可选调度方案集，依据式(1)～(3)计算各可选调度方案决策值见表1。初始优化调度方案如图1。

图1 初始调度方案

决策指标可选调度方案F1F2F3F4F5F6Rh1．211．131．061．261．151．08Eh2．322．111．942．212．061．91

表1用于分析可选调度方案的优劣，指标越小，方案越优。例如，可选调度方案F3的工序相似性指标值为1.06，是所有方案工序相似性指标的最小值，则说明在工序相似性指标方面，可选调度方案F3最好。

3.1 重调度决策方法

Step2:基于表1数据，根据式(7)建立加权标准决策矩阵：

(14)

Step3:依据式(8)，确定加权标准决策矩阵的正、负理想解：

F+={0.46,0.37}F-={0.55,0.45}

(15)

表2 可选调度方案评价

表2中，相对贴近度Ah表示可选调度方案的优良程度，按照相对贴近度Ah从大到小对可选调度方案排序，可得方案的排序序列为：F3≻F6≻F2≻F5≻F1≻F4。

Step5:依据排序序列，可得重调度方案集为φR={F2,F3,F5,F6}，则触发重调度，并选取相对贴近度最大的可选调度方案F3作为最优重调度方案来执行重调度。最优重调度方案如图2。

图2 最优重调度方案

由图2可知最优重调度方案的完工时间为55，与图1初始调度方案的完工时间相同，即重调度后没有出现完工延迟，则说明最优重调度方案有效，进而表明重调度决策方法的方案选择是合理的。

3.2 改进TOPSIS性能分析

为进一步验证决策方法的性能，针对可选调度方案的优劣排序问题，将本文的改进TOPSIS的方法与传统TOPSIS方法、正交投影法[15]、夹角余弦法[16]进行对比，各方法的具体结果见表3。

表3 各方法的方案相对贴近度

依据表3数据，确定各方法关于可选调度方案优劣关系，结果见表4。

表4 各方法的方案优劣排序

方法可选调度方案优劣排序序列改进TOPSISF3≻F6≻F2≻F5≻F1≻F4传统TOPSISF3=F6≻F2≻F5≻F1≻F4正交投影法F3≻F6≻F2≻F5≻F1=F4夹角余弦法F3≻F6≻F5≻F2≻F1≻F4

由表4中可选调度方案排序序列对比可知，改进TOPSIS、传统TOPSIS、正交投影法和夹角余弦法获得的方案优劣排序序列大体一致，均认为F3是最优的，同时F4是最差的。但传统TOPSIS、正交投影法和夹角余弦法产生的排序序列都有一定的不足，传统TOPSIS与正交投影法中都出现个别方案相对贴近度相等的情况，致使方案优劣无法区分，其中传统TOPSIS中F3和F6相对贴近度相等，正交投影法中F1和F4相对贴近度相等；夹角余弦法中F2和F5的相对贴近度大小比较结果与其他方法不同，导致F2和F5在排序序列中的位置颠倒。而改进TOPSIS除了方案排序序列与传统TOPSIS的方案排序序列基本一致以外，还能够规避其他方法存在的风险，如方案相对贴近度相等而导致无法区分方案优劣，或者出现方案优劣排序相反的现象，这说明了本文的改进TOPSIS具有较好的评价效果，进而验证了基于改进TOPSIS的重调度决策方法是可行有效的。

4 结论

(1) 从重调度耗损角度出发，基于工件和机器两个层面构建重调度决策指标，对重调度过程中可选调度方案相对于原调度方案性能进行定量描述和分析，为可选调度方案优劣评价提供依据。

(2) 提出基于改进TOPSIS的重调度决策方法，为重调度判定和最优重调度方案选择提供科学手段，并通过算例分析及改进TOPSIS与传统TOPSIS、正交投影法、夹角余弦法的对比，验证了该决策方法的有效性。

[1]VieiraGE,HerrmannJW,LinE.Reschedulingmanufacturingsystems:Aframeworkofstrategies,policies,andmethods[J].JournalofScheduling, 2003, 6 (1): 39-62.

[2] 阎志华, 丁秋林. 用蜂群算法实现动态作业车间调度[J]. 组合机床与自动化加工技术, 2004(2): 47-48,50.

[3]AkkanC.Improvingschedulestabilityinsingle-machinereschedulingfornewoperationinsertion[J].Computers&OperationsResearch, 2015, 64: 198-209.

[4]HaruhikoS.Anewwhen-to-schedulepolicyinonlineschedulingbasedoncumulativetaskdelays[J].InternationalJournalofProductionEconomics, 2007, 110(1/2): 175-186.

[5]KopanosGM,Capon-GarciaE,EspunaA,etal.CostsforReschedulingActions:ACriticalIssueforReducingtheGapbetweenSchedulingTheoryandPractice[J].Industrial&EngineeringChemistryResearch, 2008, 47(22): 8785-8795.

[6]KaoHP,WangB,DongJ,etal.Anevent-drivenapproachwithmakespan/costtradeoffanalysisforprojectportfolioscheduling[J].ComputersinIndustry, 2006, 57(5): 379- 397.

[7] 乔非, 李莉, 王遵彤, 等. 面向半导体生产的改进的混合重调度策略研究[J]. 计算机集成制造系统, 2007, 13(3): 558-562.

[8]PetrovicD,DuenasA.Afuzzylogicbasedproductionscheduling/reschedulinginthepresenceofuncertainDisruptions[J].FuzzySetsandSystems, 2006, 157(16): 2273-2285.

[9] 刘明周, 张玺, 张铭鑫, 等. 基于损益云模型的制造车间重调度决策方法 [J]. 控制与决策, 2014, 29(8): 1458-1464.

[10]ZakariaZ,PetrovicS.Geneticalgorithmsformatch-upreschedulingoftheflexiblemanufacturingsystems[J].Computers&IndustrialEngineering, 2012, 62(2): 670-686.

[11] 王学军, 郭亚军. 基于G1法的判断矩阵的一致性分析[J]. 中国管理科学, 2006, 14(3): 65-70.

[12] 李正明, 施诗, 潘天红, 等. 基于灰色关联度和理想解法的电能质量综合评估方法[J]. 电力系统保护与控制, 2014, 42(6): 14-19.

[13] 赵萌, 邱菀华, 刘北上. 基于相对熵的多属性决策排序方法[J]. 控制与决策, 2010, 25(7): 1098-1100.

[14] 刘明周, 单晖, 蒋增强, 等. 不确定条件下车间动态重调度优化方法[J]. 机械工程学报, 2009, 45(10): 137-142.

[15] 华小义, 谭景信. 基于“垂面”距离的TOPSIS法—正交投影法[J]. 系统工程理论与实践, 2004, 24(1): 114-119.

[16] 刘树林, 邱菀华. 多属性决策的TOPSIS夹角度量评价法[J]. 系统工程理论与实践, 1996, 16(7): 12-16.

(编辑 李秀敏)

Rescheduling Decision Method of Manufacturing Shop Based on Improved TOPSIS

LIU Zhuang, ZHANG Zhong-min, DU Xian-jun

(School of Mechanical and Automotive Engineering, Hefei University of Technology, Hefei 230009, China)

Aiming at the schedule selection problem of rescheduling in manufacturing shop, a rescheduling decision method based on improved TOPSIS is proposed. Firstly, the set of optional schedules is taken as the research subject, and then considering consumption in schedule changing process, the procedure similarity decision index and additional machine energy consumption decision index is established in order to depict performance of the optional schedules. Secondly, the partial order of optional schedules is ascertained by improved TOPSIS which is based on Kullback-Leibler divergence and grey correlation degree, which determines whether or not reschedule and chooses the optimal reschedule. Finally, an example is given to demonstrate the rationality and validity of the rescheduling decision method.

decision index; improved TOPSIS; rescheduling decision method

1001-2265(2017)01-0157-04

10.13462/j.cnki.mmtamt.2017.01.043

2016-03-01；

2016-04-08

刘壮(1990—)，男，黑龙江绥芬河人，合肥工业大学硕士研究生，研究方向为智能优化与生产调度研究，(E-mail)linglin8787@126.com。

TH186；TG65

A