航发叶片的测量数据误差处理方法研究*

张明德，罗 冲，张卫青，蔡汉水，谢 乐

(重庆理工大学 机械工程学院，重庆 400054)

航发叶片的测量数据误差处理方法研究*

张明德，罗 冲，张卫青，蔡汉水，谢 乐

(重庆理工大学 机械工程学院，重庆 400054)

针对航空发动机精锻叶片自动化生产线加工环境相对较差时的误差评定问题，根据国内叶片实际检测中常用的截面法检测，提出了测量点集与理论截线的优化匹配算法。该方法包含测量点集与理论截线的初步匹配、精确匹配、匹配优化，并为了得到更精确的叶型误差，根据测量点集与理论截面线之间的关系，提出了一种测量点集到理论截线的最近点集求解算法。通过实例验证了该方法的实用性和有效性，提高了检测效率，提升了测量精度，为后续精加工处理提供数据依据。

叶片测量；数据处理；匹配；航发精锻叶片

0 前言

航空发动机精锻叶片(以下简称“航发叶片”)型面属于自由复杂曲面，自由曲面测量是目前的研究热点。测量方法分为非接触式(光学测量)和接触式(CMM测量)两种方式。文献[1]对自由曲面测量技术进行了综述。文献[2-3]对自由曲面光学测量进行了研究，光学测量速度高，但精度相对接触式测量较低。国内在实际加工中，批量检测大多采用专用量具及白光来检验，并不能得到精确的叶型误差值；精加工则采用三坐标测量机进行测量，可以得到具体的误差值，不过相对效率不高[4]。

陈贵林等[5]提出航空发动机精锻叶片数字化生产线，并要求在数字化生产线内实现“自感知、自适应、自诊断、自决策、自修复”功能。在航发叶片磨削生产中提出自适应磨削加工，根据余量控制磨削区域、磨削压力，从而实现自适应磨削，提高叶片加工精度、减少叶片报废率。数字化生产线、自适应磨削加工需要检测系统提供精确的测量数据得到加工余量。为了保证自适应生产加工，设计一套快速、可靠的检测系统尤为重要。故本文针对磨削加工生产线加工环境差的问题，提出一种测量点集与理论截线的优化匹配算法，降低系统误差对测量结果精度的影响。在此测量方法的基础上，为了得到更精确的叶型误差，根据测量点集与理论截面线之间整体对应的关系，提出一种适合优化匹配算法的测量点集到理论截线的最近点集求解算法。该方法能快速得到精确的实际叶型误差值，为后续加工处理提供数据依据。

1 航发叶片测量数据处理思路

航发叶片三坐标检测主要流程有：首先，对测头进行标定，确定测头实际半径值；其次，根据检测叶片或者专用夹具建立测量坐标系，并根据叶片理论模型进行检测截面以及检测点的规划(即检测路径规划)，软件自动生成测量程序；然后，由三坐标检测机进行检测，得到测量点的坐标；最后，对测量数据进行处理，生成检测报告。

由于三坐标测量机本身的限制，测量数据处理一般需要进行后续处理，包括异常点处理和测头半径补偿。由于测量坐标系与理论坐标系不一致，测量数据需进行测量点集到理论截线的匹配，以得到最优检测结果。

(1)异常点处理

叶片检测过程中由于实物几何特征和测量手段的制约，在叶片检测结果中会出现因覆盖测量或测量数据出错等原因造成的“坏点”，以及由部分盲区或缺口而形成的“跳点”。这会影响后续数据的处理，为了保证所测截面数据的正确性和完整性，所以需要对“坏点”和“跳点”进行处理。

对于坏点可以通过人工观察、弦高差方法[6]等进行处理。对于跳点可以通过截取理论模型部分来填补，也可通过重新规划检测路径来处理。

(2)测头半径补偿

由于叶片型面是自由曲面，测量过程中测头采用不补偿的模式，测量机输出的数据是测头球心的坐标，故需对测头半径进行补偿。关于测头实际半径一般通过测头标定[7-9]来确定，然后进行补偿。本文采用测量点沿其法矢向内平移一个测头半径来进行测头半径补偿。

(1)

式中： (xi，yi，zi)—实际测量点坐标；

(xi′，yi′，zi′)—测量球心点坐标；

(ii，ji，ki)—测量点单位法矢的坐标分量；

r—测头实际半径。

(3)测量点集到理论截线的匹配

对测量数据进行处理时，其中最重要的一环就是实现测量数据与叶片理论模型的精确匹配，即通过匹配使叶片实际测量点相对于理论模型的误差达到最小，从而减小系统误差的影响。

航发叶片三坐标测量大多采用截面法进行测量，且叶片设计时允许各截面存在一定的误差偏值(一般轮廓度误差为0.08mm，扭转误差为±12′)，所以叶片的测量数据匹配问题可转化为平面内测量点集与理论截线的匹配问题。

2 测量点集到理论截线的最近点集求取

由于测量点集到理论截线的匹配是以测量点集到理论截线的距离平方和最小为目标函数，所以求取测量点集到理论截面所得的最近点集将对匹配结果有很大的影响。

针对点到复杂平面曲线最近距离的算法有基于几何特征的快速迭代法[10]、分割逼近法快速求解点到复杂平面曲线最小距离[11]、迭代最近点算法(ICP)[12-13]等。但这些算法均是针对点到曲线的最近距离求解，而本文研究的重点是求解测量点集整体到封闭曲线的最近点集。求解过程中可能会出现两个问题：一是同一点存在两个或两个以上的最近点，如图1中测量点Pi到理论截线上Qi与Qi′距离一样；二是某测量点在曲线上所对应的最近点并不在其前一点与后一点在曲线上所对应的最近点区域范围内，如图1中测量点Pi+1在理论截线上对应点Qi+1,并不在Pi-1与Pi+2对应最近点Qi-1与Qi+2之间，这与测量点集与叶片理论截面线对应关系不符。

图1 对应关系混乱的测量点

测量点集在理论截线上所对应的最近点集应该满足与截面线按次序分布的关系。本文通过对比对应最近点在曲线上的参数值来解决该问题。

测量点集在理论截线上的最近点集求取的具体流程图如图2所示。

图2 最近点集求取流程图

(1)航发叶片截面形状是复杂封闭曲线，但整体较光顺，所以本文按等参数将其分割为n份(根据叶片大小确定)，并求取测量点P(x,y,z)与各控制点Qi(xi,yi,zi)之间的距离：

(2)

求取n个端点与测量点的最小距离：

dmin=min(d1,d2,…,dn-1,dn)

(3)

则测量点的最近点位于与dmin对应控制点Qi两侧邻域中，如图3所示。

图3 控制点中找取最近点

(2)将最近控制点两侧邻域按参数U值分别等分为两个小曲线段，求取测量点与各控制点的距离，如图4。

图4 邻域划分方法

(3)如果其邻域

(4)

式中：Us—点Qi-1在曲线上对应的U值，

Ue—点Qi+1在曲线上对应的U值，

Δ—设定误差值。

则该点为最近点，如果不满足上式，则转到第(2)步，继续求解。

(4)因为测量点集就是沿着顺时针/逆时针进行测量得到的，所以理论上其对应最近点集在理论曲线上也是按此规律进行分布的，在测量点集各自对应的最近点集中寻找其在理论截线上的U值规律，找出不符合规律的测量点。

(5)将不满足规律的测量点，在其前一点和后一点的U值范围中重新找取最近点，保证对应点集求取的正确性、规律性。

该方法可以保证测量点集与其在理论截线上的对应最近点集按规律分布，但也存在一定缺点，如果不规律点过多，则计算效率会非常低。

3 测量点集与理论截线的优化匹配算法

3.1 初步匹配

根据第2节所描述的算法，虽然解决了测量点集对应的最近点集的规律性，但测量点与理论曲线距离较远时，最近点对应关系混乱，如图5所示，则计算效率较低，所以最好将之移动到相近位置再进行计算。而曲线形状与曲面所在空间坐标系无关，且具有空间移动不变性，故选取曲线形状特征作为初始匹配要素。

图5 对应最近点混乱的情况

(1)考虑到封闭曲线的特征，首先通过两封闭曲线的几何中心将之平移到相对靠近的位置。

计算叶片截面线的几何中心M1和全部测量点的几何中心M2(理论截线方程未知，无法运用积分法进行几何中心求解，故采用等参数法将其分割为n份，用点集的几何中心近似表示)

(5)

将测量点集整体沿矢量

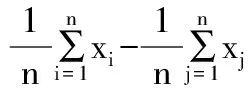
(6)

平移，平移结果如图6中Pi′所示。

图6 测量点平移示意图

(2)航发叶片多为片状，本文采用分别计算截面曲线和测量点集中距离最远的两点，连接它们生成的直线l1、l2，以其矢量V1、V2的夹角为旋转角度，将之近似对齐。

将测量点集旋转角度

(7)

其中：V1，V2分别代表l1、l2的矢量。旋转结果如图7中Pi所示。

图7 测量点旋转示意图

3.2 精确匹配

由于采用理论截面线为匹配基准，所以为了提高匹配精度，每次迭代后，重新求取变换后测量点集在理论截线上的对应最近点。其中测量点Pi(xi,yi,zi)，通过第2节所述最近点集的求取算法，获得每点所对应的最近点Qi(ai,bi,ci)。

测量点集到理论截线的匹配模型适合度函数选择点集到截线的误差平方和，则目标函数为

(8)

式中：

Pi—实际生产模型上实际点的坐标；

Qi—CAD模型上与实际生产模型上点最近点的坐标；

di—实际生产测量点与CAD模型上截面线的最点的距离；

2.2.4 结果比较 3种预处理方法得到的枸杞子外观和色泽无显著差异；但特性量值是否发生显著变化需要进一步实验加以验证；但减压干燥法较液氮冻干法、冻干法更省时，节能。

R—旋转矩阵

；

T—平移矩阵

。

即

(9)

由最小二乘法可知，当距离的平方和最小时才满足校准要求，因而得到最小目标函数如下：

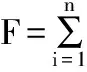
(10)

把式(9)代入式(10)可得：

(11)

要使该式取得最小值，需满足三个偏导数都为零，即：

(12)

通过计算：

(13)

式中：

即可先算出γ，再代入式(13)即可求出Lx，Ly，代入平移及旋转矩阵。最后由最小二乘法根据计算误差限定值ε进行匹配。

3.3 匹配优化

通过观察匹配结果可知：目标函数匹配每次迭代得到的变换结果之间存在一定的规律，这个规律是当迭代次数超过20次后误差平方和变化不大，由图8a可见；最大误差值在20次迭代左右出现极小值，由图8b可见。

(a)每次迭代的误差平方和 (b)每次迭代的最大误差值图8 目标函数匹配结果

经多次实验验证，上述规律均存在，由此可确定测量点集转换后的最大误差值应该存在一个最小值，该值必定位于目标函数匹配中最大误差值取得极小值时的上次变换与下次变换的区间内。采用区间搜索法寻找叶片真实最大误差值的最小点所对应的变换矩阵，这时的变换矩阵即本文所要求的坐标变换矩阵。

本文采取误差平方和最小和最大误差值最小两种评判准则进行整体分析，相对只是目标函数求解可减少1/2～2/3的迭代次数，并将最大误差控制在较小范围内。其优化思路为：当迭代过程中出现误差最大值开始变大时，停止最小二乘法迭代。同时，提取误差最大值最小时变换矩阵的参数(Lxm，Lym，γm)，以及上一次迭代和下一次迭代的变换矩阵参数(Lxs，Lys，γs)和(Lxe，Lye，γe)，将两侧区域分别划分为相同大小的区域，计算各自控制点转化后误差最大值，其最优变换结果一定位于误差最大值最小时对应变换值的邻域中，直到邻域小于给定误差限定值δ时，认为此转换矩阵为最优变换矩阵。将测量点集经最优转换矩阵转化后得到最终测量值Piz(xiz,yiz,ziz)。

匹配优化流程图如图9所示。

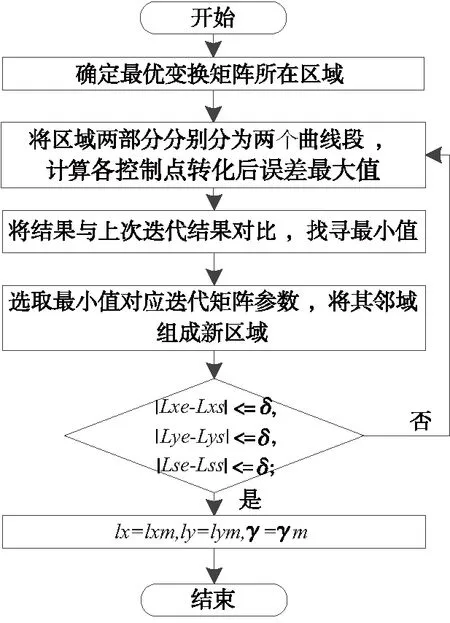
图9 测量点匹配优化流程

4 实例验证

将某航发叶片(如图10)在海克斯康三坐标测量机上进行测量，测量结果进行测头半径补偿后采用本文算法进行后续处理。

图10 检测中的航发叶片

航发叶片某一检测截面数据处理如下：原始点数据如图12a所示，其中初始匹配、精确匹配、匹配优化所需变换矩阵参数如图11所示，最终转换结果如图12b所示。

(a)坐标平移距离

(b)坐标旋转角度图11 最小二乘法迭代示意图

(a)测量原始点 (b)测量点集匹配结果图12 测量数据原始点与匹配后的对比

对于同一叶片，根据图纸检测要求一般检测多个截面，本文所检测叶片体积较小，故检测了5个截面。图纸要求检测截面间允许轮廓度误差为0.08mm，扭转误差为±12′，而本文所提供算法所需坐标变换值如下表所示，X方向最大偏移误差为0.07458mm，Y方向最大偏移误差为0.08598mm，最大旋转误差为0.00106°(约为0.06′)，完全符合要求。

表1 偏移结果数据

本文研究优化匹配算法所得数据与市场上常用海克斯康三坐标检测机匹配数据对比结果如图13所示。

图13 匹配结果与海克斯康匹配结果对比

其中，匹配结果与海克斯康基本一致，但本文所提优化匹配算法最大误差值为0.36795，海克斯康系统结果则为0.3802。

5 结论

本文提出了一种求解点集到封闭曲线的最近点集的算法，保证测量点集在曲线上对应最近点集的连续性，为测量点集与理论截线的优化匹配算法做基础。测量点集与理论截线的优化匹配算法与单一目标匹配优化方法相比，效率大幅度提升；与海克斯康检测结果基本一致，精度方面有所提升。实例验证该算法是可行的，可为后续加工生产提供数据依据。

[1] LI Yadong ,GU Peihua. F surface inspection techniques state of the art review[J]. Computer-Aided Design,2004,36(13);1395-1417.

[2] 张新,许英朝. 光学自由曲面的检测方法[J]. 中国光学与应用光学,2008,1(1):92-99.

[3] CHUN B S, KIM K,GWEON D, et al. Three-dimensional surface profile measurement using a beam scanning chromatic confocal microscope[J]. Review of Scientific Instruments,2009,80(7):30-34.

[4] 俞学兰,叶佩青. 航空发动机压气机叶片型面检测技术[J]. 航空制造技术,2007(11):46-48.

[5] 陈贵林,赵春蓉. 航空发动机精锻叶片数字化生产线[J]. 航空制造技术,2015(22):78-83.

[6] 陈福兴. 基于UG叶片型面测量分析技术的研究[D].无锡:江南大学,2006.

[7] 高健,陈岳坪,邓海祥,等. 复杂曲面零件加工精度的原位检测误差补偿方法[J]. 机械工程学报,2013,49(19):133-143.

[8] 赵铭,张卫青,张明德. 大型数控插齿机在线测量测头标定方法[J]. 重庆理工大学学报(自然科学),2012,26(2):60-63.

[9] 张白,石照耀. 三维扫描测头的标定方法[J]. 北京工业大学学报,2013,39(4):481-486.

[10] 伍丽峰,陈岳坪,谌炎辉,等. 求点到空间参数曲线最小距离的几种算法[J]. 机械设计与制造,2011(9):15-17.

[11] 廖平. 分割逼近法快速求解点到复杂平面曲线最小距离[J].计算机工程与应用,2009,45(10):163-164.

[12] Besl P J,N D Mc Kay.A method for registration of 3-D shapes[J].Pattern Analysis and Machine Intelligence, IEEE Transactions on, 1992:586-606.

[13] 许治,戴宁,张长东,等. 基于迭代变形的多源数据融合技术[J]. 机械工程学报,2014,50(7):191-198.

(编辑 李秀敏)

Research on Processing Method of Measuring Data Error of Precision Forging Aeroengine Blade

ZHANG Ming-de，LUO Chong，ZHANG Wei-qing，CAI Han-shui，XIE Le

(School of Mechanical Engineering,Chongqing University of Technology,Chongqing 400054,China)

Aiming at the problem of error evaluation when the processing environment of the automatic production line of the precision forging aeroengine blade is relatively poor, an optimal matching algorithm of the measuring point set and the theoretical truncation line is proposed according to the cross section method commonly used in the domestic blade actual inspection. The method includes the initial match, the exact match and the matching optimization of the measurement point set and the theoretical stub.In order to obtain a more precise leaf shape error, a new algorithm for finding the closest point set between the measurement point set and the theoretical stub is suggested based on the relationship of the measurement point set and the theoretical section line. The examples were used to verify the effectiveness and practicality of the proposed method,improves the detection efficiency and improve the measurement accuracy, the data provide a basis for subsequent finishing process.

blade measurement；data processing；matching；precision forging aeroengine blade

1001-2265(2017)01-0057-05

10.13462/j.cnki.mmtamt.2017.01.016

2016-09-26

“高档数控机床与基础制造装备”国家科技重大专项项目航空发动机精锻叶片自适应砂带磨削中心研制及其应用(2014ZX02001031);国家自然科学基金(51275545)

张明德(1975—)，男，四川苍溪县人，重庆理工大学副教授，硕士，研究方向为复杂曲面零件智能化设计制造及检测，(E-mail)zmd@cqut.edu.cn；通讯作者：罗冲(1990—)，男，河南南阳人，重庆理工大学硕士研究生，研究方向为复杂曲面零件智能化设计制造及检测，(E-mail)873886891@qq.com。

TH166;TG506

A