信道模型的研究与应用
田 媛
(西安航空学院 电子工程学院,陕西 西安 710003)
0 引言
大多数科学家都认为,信息理论始于香农发表于1984年的那篇著名论文[1]。在那篇论文中,他提供了以下问题的答案:
—什么是“信息”,以及如何衡量它?
—存储和信息传输的基本限制是什么?
答案既令人满意又令人惊讶。而最令人震惊的是,他们将复杂问题简化为简单的分析形式的能力。从那时起,信息理论一直在设计能够达到或接近这些极限的设备。
在远距离通信和计算机网络中,将数据从一个位置传输到另一个位置,需要某种形式的途径或媒介。这些被称为“交流通道”[2]的路径,可以指的是一种物理的传递介质,例如一根电线,也可以是指在一个多路传输介质上的逻辑连接,例如一个无线电通道。信道主要用来从一个或几个发送者(或发射机)到一个或多个接收器之间传送一个信息信号,例如一个数字比特流。信道有一定的传输信息的能力,通常是用赫兹的带宽或每秒比特的比特率来测量[2]。
1 香农理论
将信息从发射机传送到接收机的过程可以被描绘成图 1。这个被称为“香农范式”的模型是通用的,适用于各种各样的情况。

图1 香农理论模型
它主要表述了以下几部分内容:
(1)信息来源是一种从字母表中随机传递符号的装置。
(2)信道是一个将发射机与接收机连接的系统。它包括信号设备和铜线、同轴电缆或光纤,以及其他的可能。若给定一个接收到的输出符号,由于随机环境噪声和信号处理的不完善,系统并不能确定输入的符号被正确传递。
(3)一个信源编码器可以通过消除冗余来更简洁地表示数据源,它的目的是降低数据的速率。
(4)信道编码器通过增加冗余来保护传输信号不受传输错误的影响。
(5)信源和信道解码器与信源和信道编码器工作原理相反。
因此,“信源编码”和“信道编码”之间存在二重性,前者倾向于降低数据速率,而后者则需要提高它。
2 信道的基本分析
一般来说,信道可以划分为“无记忆信道”和“有记忆的信道”[3]。在这里,我们首先关注基于离散无记忆信道(DMC)的分析。因为它结构简单,更容易解释和理解。
作为前文提到的通信系统的一部分,我们可以看到离散的无记忆信道(DMC)有一个输入 X和一个输出Y,如图2所示。
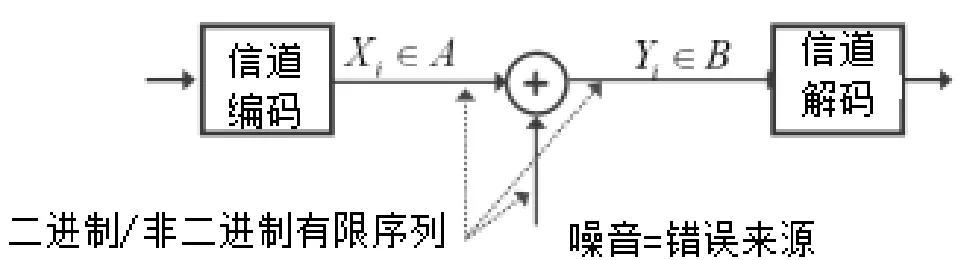
图2 DCM结构
随机信号X和Y都是离散的,且可以取有限数量的可能值。所以有:
信道输入序列: X0, X1, ......, Xi,Xiє A。其中A取有限值映射表: A={a1, a2, ..., aq};q为映射表的大小。
信道输出序列: Y0,Y1, ......, Yi,Yiє B。其中B取有限值映射表: B={b1, b2,..., br};r为映射表大小。
在某一特定时间t,信道的输出Y=y仅依赖于信道在t时刻的输入X=x,与之前的历史输入无关。因此,转移概率分布是Y0=y0, Y1=y1,…, Yn-1=yn-1的条件联合概率,其条件为:X0=x0, X1=x1,…, Xn-1=xn-1。故可以表述为:

联合概率分布还可以写为联合概率矩阵。信道矩阵 T={tij}被定义为已知输入信号 xi的概率和输出信号yj的概率的传递矩阵:
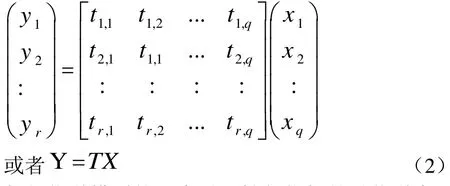
任何信道模型的一个重要性能指标就是信道容量(Channel Capacity,C),在原则上,信道容量即是一个信道可以携带的“最大信息量”。因此,通道容量为通道性能提供了“上限”(就信息传输的级别而言)。通道输入X和信道输出Y之间的互信息I(X;Y)提供了一种可以由通道承载的“信息量”的度量,是信道容量的信息理论定义。因此,“信息”通道容量C被定义为信道输入和输出之间的“最大相互信息”。
香农的信道容量公式(所有速率R的最高值,其中存在一串有消失的错误概率的编码序列,其大小随块长度n为exp(nR)),主要针对无记忆信道。

若信道有记忆,那么它通常表述成为另一种近似的表达[4]。

香农还证明:当传输速率不超过下式中 C的值时,在数字信道中是可以实现无错误的传输的。
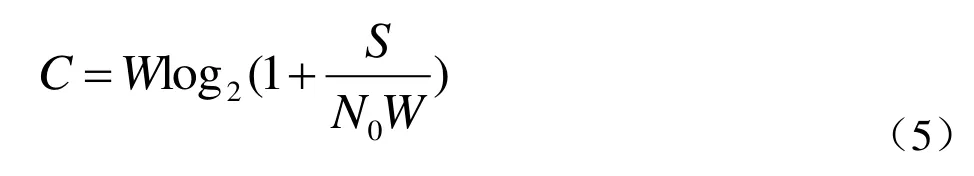
其中S为信号强度;w为信道带宽;N0位单边噪音强度密度。并且信道增益被假定为在整个带宽W上统一等于一个单位,而在其他地方则为零。信道的噪声被认为是高斯噪声和白噪声。因此,C的值也被称为信道容量或香农极限[5]。
3 信道模型
信道可以通过尝试调整传输信号,并计算其物理过程来进行物理建模。信道模型在设计和开发多媒体应用方面起着至关重要的作用。例如,理解通道损害对通过这些通道传输的压缩数据的影响是非常重要的。常用的模型包括:无损通道、确定通道、均匀通道、二进制擦除通道(BEC)和二进制对称信道(BSC)。这些信道的扩展也用于在具体应用中模拟更现实的场景。
3.1 附加噪声信道(AWGN)
附加噪声信道(The additive noise channel)是最简单的一类信道数学模型是,如图3所示。在这个模型中,传输信号 s(t)被一个附加的随机噪声过程 n(t)干扰。实际过程中,噪声的附加过程可能来自于通信系统的接收方的电子元件和放大器,或者是在传输过程中遇到的干扰,就像无线电信号传输的情况一样[6]。
如果噪音主要是由电子元件和放大器的放大器所引入,它可以被描述为热噪声。这种噪声实际上和高斯噪声的过程类似,因此,该信道的数学模型通常被称为附加高斯噪声信道[6]。由于它的数学可跟踪性,该信道模型成为适用于广泛的物理通信信道,因此它也是在通信系统分析和设计中使用的主要信道模型。
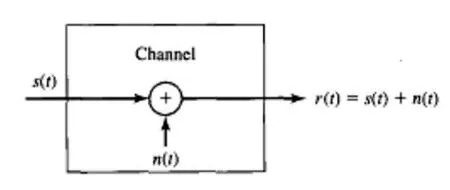
图3 AWGN结构示意图
该信道衰减很容易被合并到模型中。当信号通过信道传输衰减时,接收到的信号是

其中,a代表衰减因子。
3.2 二进制擦除信道(BEC)
二进制擦除通道(The binary erasure channel)可能是最简单且非平凡的通道模型,但是它们(及其扩展)被广泛用于包括“丢失”数据的信道或链接。该模型原本是Elias在1954年作为一个玩具提出的例子,但是由于互联网的出现,促进了擦除信道进入了“真实世界”的使用范围。
在擦除信道模型中,信息可能会丢失,但不会被干扰破坏。BEC以最简单的形式捕捉了擦除:即,单个比特被传送时,要么被正确接收,要么被丢失。因此,解码的关键是确定找到给出码字的擦除部分和未擦除部分的比特位的值。
图4描绘了BEC(p)的基本结构。时间t是离散的,发射机和接收器是同步的(均以t为参考)。t时刻,输入信号X(t),该信号是二进制的,即此时,对应的输出可以映射为其中,?表明一个擦除。每一位的传输都伴随着是概率为 p的擦除可能性,或者正确的接收。即:擦除在每一个时刻t都是独立发生的。因此,我们也可以说通道是无记忆的[7]。
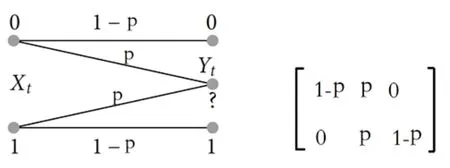
图4 BEC的基本结构和矩阵
BEC(p)的信道容量是CBEC(p)=1-p位/使用信道。很容易看出:如果n位被传输,那么平均(1-p)n位被接收(并且被正确地接收)。根据大数定律,对于很大的n时,实际(正确)接收位数很可能接近这个平均值。因此,即使发送者和接收方事先知道哪些位将被删除,信息也可以以最多 1-p位/使用信道的速率进行可靠传输。也许令人惊讶的是,以任意接近1-p的速率进行可靠传输均是可能的[7]。
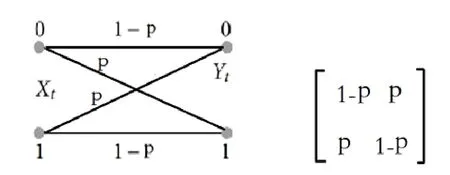
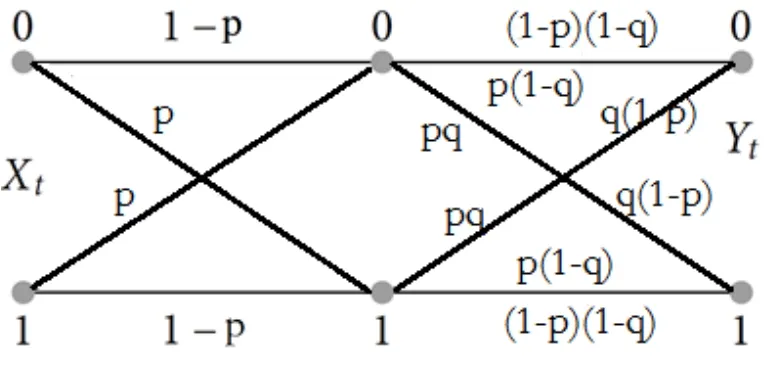
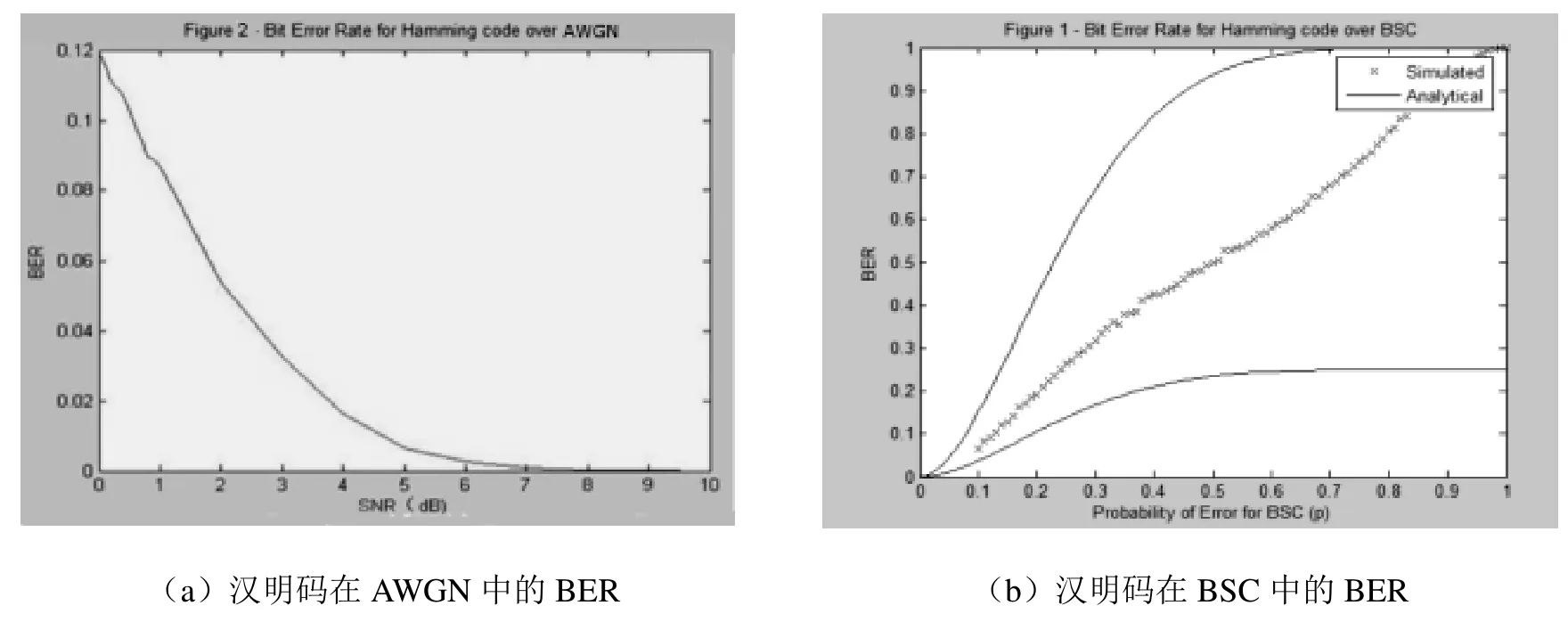
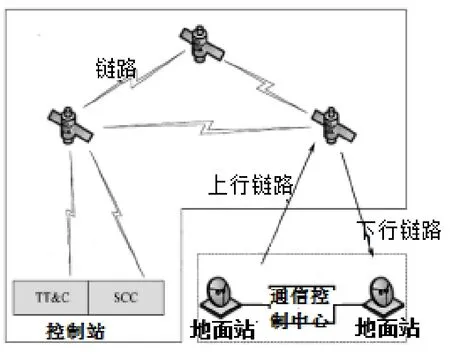
考虑信道在以下情况级联:给定两个参数,p和q,p 图5 两个BEC级联示意图 二进制对称信道(The Binary Symmetric Channel)模型(及其扩展)被广泛用于展示存在错误的通道或链接,例如无线连接和低质量的有线通道。图6描述了BSC(p)的基本模型。 图6 BSC基本结构与矩阵 时间 t是离散的,发射机和接收器是同步的(且均以 t为时间参考)。在t时刻的输入,由X(t)表示,它是二进制的,即 X(t){0,1}。对应时刻的输出Y(t)可取{0,1}。这显示出BSC与BEC的明显不同,并以下列条件概率为特征(在信道矩阵中显示相同): 与BEC模型不同,在BSC中,接收的位(即使它们是正确的),我们也不知道它们是否是正确的;因此,对于接收到的比特的正确性,存在着一种不确定情况[8]。从概念上讲,如果接收到的位被干扰损坏,我们可以通过“通知”接收端来解决这种不确定性。这反过来相当于在每次从输入端 X传递一位信息的同时,“发送”一个“代码”,用于通知接收者 BSC的信道状态(或者是否产生错误)。因为这里的信息是二进制的,所以它与一个“二进制源”的熵相同,该二进制源有以下条件概率函数因此,在接收端收到的信息中,与输入信息X有关的有效(最大)信息是:1位(传输的X位)减去用来表示信道状态的位数(用 H(ε)表示),即: 与 BEC的级联情形类似,这里假设这些级联BSC通道的错误参数p和q是独立的,如图7所示。因此,p的值不会影响q,即与q无函数关系,反之亦然。在这种情况下,一个端到端的错误只可能在这种情况下发生:一个错误发生在第一个BSC信道(误差参数p)并且没有错误在第二个BSC信道(错误参数q);或没有错误发生在第一个 BSC信道和一个错误发生在第二个BSC信道。因此,在两个级联的BSC通道上,有错误参数p和q: 图7 BSC通道级联示意 因此,两个级联的BSC通道可以被看作是一个单独的BSC通道,其整体损失参数为A[8]。 为了更好地理解信道的概念,我们可以使用计算机软件,如 MATLAB,进行模拟。将不同类型的代码通过不同的信号模型进行传输,并观察比较输出。在本文中,选取汉明代码应用于AWGN和BSC。 汉明码是一种线性的错误校正码,它可以检测到2位错误或纠正1位错误,而不会发现未纠正的错误[9]。相比之下,简单的奇偶校验码不能纠正错误,只能检测出奇数位的错误。因此,汉明码是更为高级的代码,它们的代码块长度和最小距离达到了最高的码率。 我们可以模拟并输出在AWGN和BSC中代码的比特误率的曲线,如图8所示。 图8 AWGN和BSC中代码的比特误率的曲线 显然,在 AWGN信道中,随着信噪比(SNR)的升高,比特误率(BER)逐渐降低,最终达到0。在BSC中,中间线是模拟的BER,而其他的线是分析的BER。从图 8(b)中,上面的黑线是当误差概率p最大时的 BER,而另一个则误差概率最小时。从结果可以得知,更大的错误概率p会导致BSC中更高的BER。 多年来,数字通信领域出现了巨大的增长,特别是在蜂窝、卫星和计算机通信领域。在这些通信系统中,信息被表示成一系列二进制数码,随后被调制到模拟信号波形,并通过信道传输。信道在传输过程中引入了噪声和干扰[10]。在接收端,被信道加入干扰的传输信号被映射回二进制位。因此,接收到的二进制信息只是对传输的二进制信息的近似估计。位错误可能是由于传输造成的,而位错误的数量取决于通信信道的噪声和干扰量。 二进制的卫星通信系统结构如图9所示。 图9 二进制卫星通信系统结构示意图 在卫星通信中,上行链路(up-link,UL或u/l)是用于从地球终端到卫星或机载平台传输信号的通信链路的一部分。向上链接和向下链接互为相反。向上链接或向下链接同时区别于反向链接或转发链接。BSS和NSS内部的通信和信号流也可以被识别为上行链路和下行链路。在计算机网络中,一个上行链路是从数据通信设备到网络核心的连接[12]。这也被称为上游连接。 在卫星通信中,下行链路(down-link,DL)是从卫星到地面站的连接。在蜂窝网络中,无线电下行链路是从一个站到手机的传输路径。在基站子系统(BSS)和网络交换子系统(NSS)之间的通信和信号流也可以被识别为上行链路和下行链路。在计算机网络,下行连接是数据通信设备与数据终端设备之间的连接[12]。这也被称为下游连接。 本文主要讨论了三种常用的信息通道模型:AWGN、BEC、BSC和它们的级联应用。通过MATLAB进行计算机仿真,证明了香农理论的实际应用。 要通过信道进行可靠的通信,传输速率就不能大于信道容量。二进制对称信道是二进制通信系统的合适模型,在这种系统中,输入和输出符号出现在一个对称的错误概率上。同时信道容量也随信道的信噪特性而变化,高速率高信噪比的传输可以由此获得。 [1]C E Shannon. A mathematical theory of communication [J].Bell Syst. Tech J., 1948(27): 379-423. [2]T, Wadayama. An introduction to performance analysis of LDPC codes [J]. Ieice Technical Report Information Theory,2002(102): 9-16. [3]Shervih, Shahidi. Robust lossy source coding for correlated fading channels[D]. Kinston, Ontario, Canada: Queen’s University, 2011. [4]Sergio, Verdn, Te SunHan. A general formula of channel capacity [J]. IEEE TRANSACTIONS ON INFORMATION THEORY, 1994, 40(4): 34-40. [5]S Tirro. Satellite Communication System Design[M]. New York: Springer Science & Business Media, 1993. [6]Bhattacharya. Digital Communication [M]. U.S.A: Tata Mc Graw-Hill Education, 2005. [7]David, J C MacKay. Information Theory, Inference, and Learning Algorithms [M]. Cambridge: Cambridge University Press, 2003. [8]Hayder, radha. Memoryless Channel Models [D]. U.S.A:Michiga State Univercity, 2008. [9]Moon Todd K. Error Correction Coding [M]. New Jersey:John Wiley & Sons, 2005. [10]U L Bomble, M B Malik. Design of Viterbi Decoder for Noisy Channel [R]. Advanced in Recent Trends in Communication Network, 2010.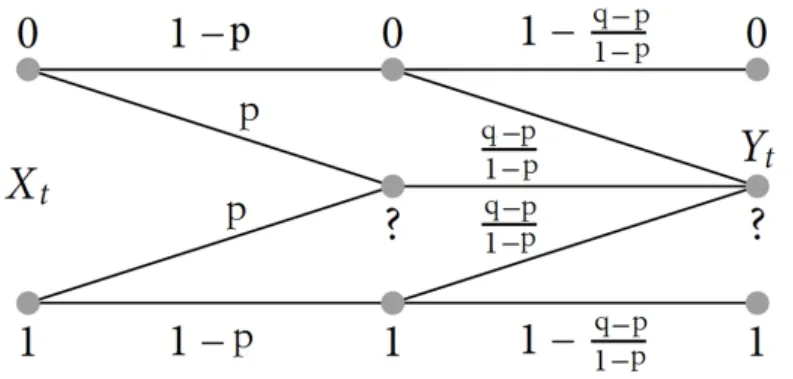
3.3 二进制对称信道(BSC)
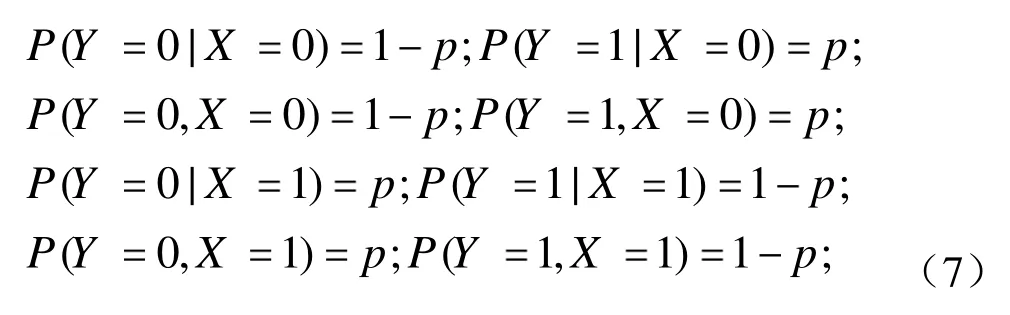
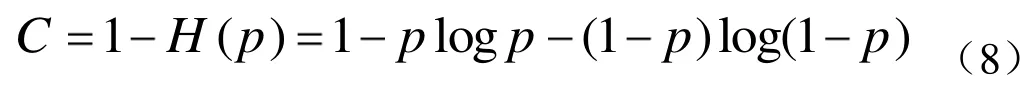
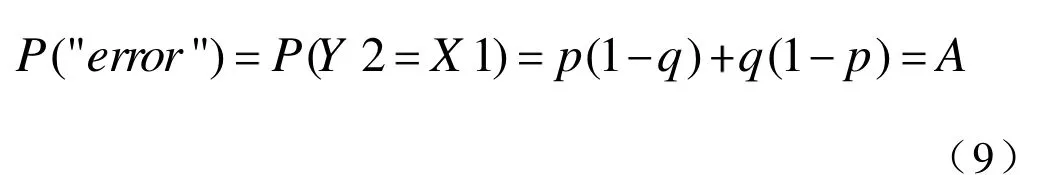
4 计算机模拟
5 信道的应用
6 结论

