某船用高压油泵壳体的模态分析

魏 镇，朱宇龙，李玉光

（大连大学 机械工程学院，辽宁 大连 116622）

高压油泵壳体是高压油泵的主要承载结构，其上连接着很多零部件，这些零部件在工作过程中产生的振动都会引起壳体振动，所以高压油泵壳体结构对高压油泵性能有着重要影响，但目前对其特性研究很少。

高压油泵壳体有限元结构模态分析是其初期结构设计的核心，同时也是后期进行结构振动和噪声分析及评价的基础。根据模态分析结果对其结构进行优化，可以延缓高压油泵的疲劳破坏，降低工作过程中的振动噪声，同时保证高压油泵向发动机及其它部件稳定供油，从而使船舶可以正常行驶。

在实际应用中由于实验成本比较大，一般在设计初期采用仿真软件来代替实验，这不仅可以缩短产品研发周期，节约大量的科研经费，同时还可以使结构优化更加合理，保证产品的质量[1]。虽然Abaqus在有限元分析中应用很广泛，但其自身包含的建模功能有很多不足之处，而Pro/E具有强大的参数化建模能力，可以建立非常复杂的三维模型，所以本文采用Pro/E来建立高压油泵壳体的三维实体模型。

1 高压油泵壳体有限元模型的建立

高压油泵内部零件众多，且大部分都连接在壳体上，所以壳体表面结构复杂。在建立高压油泵壳体模型时应该合理简化，这样既能保证结果的准确性，又能提高计算效率。

根据高压油泵壳体实际装配，在Pro/E中建立了油泵上盖、泵体、法兰盘和小端盖的组合结构三维模型，并对其中的水孔、油孔、螺纹孔及大部分凸台都进行了简化[2]。高压油泵长367 mm，高360 mm，法兰盘直径为240 mm，小端盖直径为141 mm，泵体的材料均为45钢，45钢的材料参数如表1所示。

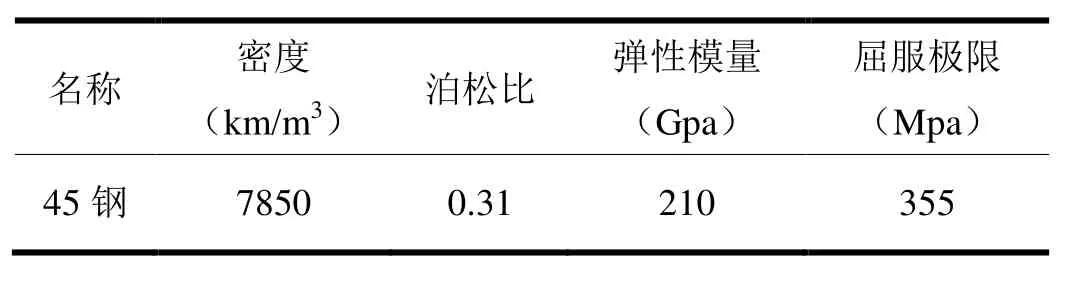
表1 材料参数

将建立好的高压油泵壳体三维几何零件进行装配，然后通过Abaqus软件内置接口，导入到Abaqus中划分有限元网格，其中左侧法兰盘处轴承盖采用HEXA8单元，其余各处采用TETRA10单元。整个模型共有150878个单元、237550个节点。高压油泵壳体的有限元模型如图1所示。

图1 高压油泵壳体有限元模型

2 高压油泵壳体的模态分析

2.1 模态分析方法

模态分析是目前研究结构动力学特性的重要方法，已经成为解决现代复杂结构动态特性设计的重要手段，模态分析对验证模型有效性和结构优化都能起到指导作用。

模态分析是将物理模型转化为模态模型，即用已知结构的几何形状、材料参数和边界条件，将结构的质量分布、刚度分布和阻尼分布分别通过质量矩阵、刚度矩阵和阻尼矩阵表示出来，从而得到系统的模态参数[3]。在计算模态参数时，一般假设结构刚度矩阵和质量矩阵不发生改变，而且结构中没有随时间变化的载荷，具体公式如下：式中，［M］是质量矩阵，［C］是阻尼矩阵，［K］是刚度矩阵，｝是位移矢量，是速度矢量，｝是加速度矢量。式中，｝是第i阶模态形状的特征向量，ωi是第i阶自然振动频率，t是时间。

由以上两个方程便可以求得高压油泵壳体的振型和固有频率值。

2.2 模态仿真计算

模态是机械结构固有振动特性，每一个模态具有特定的固有频率振型[4]，但是在进行模态分析时，一般不需要求出结构所有模态的振型和固有频率。根据实际工作情况在高压油泵的法兰盘处施加固定约束，提取了高压油泵壳体的前十阶振型和固有频率值。高压油泵的前十阶模态振型如图2所示，固有频率值如表2所示。

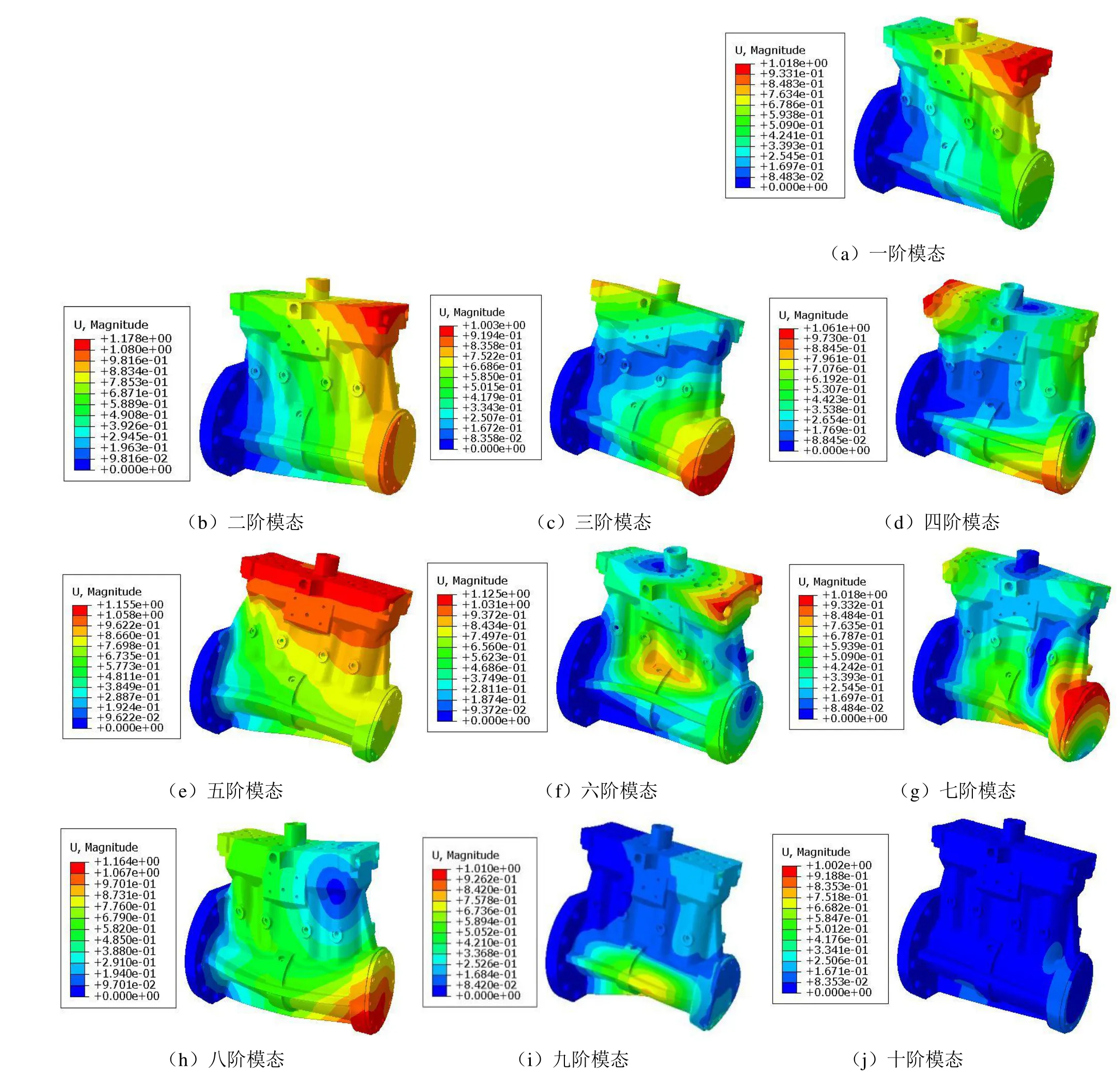
图2 高压油泵壳体的前十阶模态振型

表2 高压油泵壳体的前10阶固有频率值

2.3 仿真结果分析

从模态分析的结果可以看出，高压油泵壳体的模态振型主要表现为扭转和弯曲变形。其中1阶振型和2阶振型均为泵体和上盖的弯曲变形，最大相对变形位于高压油泵壳体上盖的右端。3阶振型为泵体的弯曲和泵体下半部分及上盖的扭转变形，最大相对变形位于高压油泵壳体上盖的左端。4阶振型为泵体、上盖和小端盖的扭转变形，最大相对变形位于高压油泵壳体底部的右端。5阶振型为泵体下半部分和上盖的弯曲变形以及泵体和小端盖的扭转边形，最大相对变形位于高压油泵壳体的上盖处。6阶振型为泵体、上盖和两端端盖的扭转变形以及泵体的弯曲变形，最大相对变形位于高压油泵上盖右侧两端处。7阶振型为高压油泵壳体整体的弯曲和扭转变形，其中高压油泵壳体下半部分变形最为明显，最大相对变形量位于泵体右侧。8阶振型为泵体和上盖的弯曲变形，最大相对变形位于高压油泵壳体底部右端。9阶振型为泵体下半部分的弯曲变形，弯曲方向与第8阶振型的弯曲方向相反，最大相对变形位于高压油泵壳体底部加强筋板处。10阶振型主要表现为法兰盘处的扭转变形，其他部位没有明显的变形，最大相对变形位于法兰盘处。

由以上的前十阶模态可以看出，高压油泵壳体形变比较大的部位多集中在壳体的上盖和底部，其中高压油泵底部的扭转和变形都比较大，主要是因为底部是安装曲轴的空腔，是薄壁结构，所以刚度较小，在设计初期可以添加合理的加强筋来保证底部结构的稳定性。

3 结论

本文利用Pro/E和Abaqus对某船用高压油泵壳体进行了模态分析，得到了其振型和固有频率值。对振型进行了描述，找出了形变比较大的部位，并对其原因进行了分析，为后续高压油泵壳体结构和整体动态特性的优化提供了参考依据。

[1]关长明. 白车身模态分析[D]. 合肥: 合肥工业大学, 2008.

[2]王鑫, 季振林. 柴油机辐射噪声预测及控制技术研究[J].噪声与振动控制, 2008(02): 87-91.

[3]王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003.

[4]吕端, 曾东建, 于晓洋, 等. 基于ANSYS Workbench的V8发动机曲轴有限元模态分析[J]. 机械设计与制造, 2012(08): 11-13.