利用李萨如图形确定频率比的一种新方法

魏慧丽，何武光†，王 昭

(1. 湖北工程学院物理与电子信息学院，湖北 孝感 432000；2. 德宏师范高等专科学校，云南 潞西 678400)

利用李萨如图形确定频率比的一种新方法

魏慧丽1，何武光1†，王 昭2

(1. 湖北工程学院物理与电子信息学院，湖北 孝感 432000；2. 德宏师范高等专科学校，云南 潞西 678400)

在大学物理教学中分析李萨如图像时，通常使用传统的方法，即切点数反比法、或十字交点数反比法确定李萨如图像水平与竖直方向分振动频率比。但切点数反比法无法确定有端点的李萨如图像的频率比，而十字交点数反比法分析时，学生容易出现较多疑问。而此提出的新的分析方法——单曲线数正比法，其分析过程与分振动物理含义结合紧密，容易理解，应用简单，对封闭以及有端点的李萨如图形分析都适用。

李萨如图形 频率比 单曲线数正比法

1 引言

在大学物理教学中，示波器在不同频率比、不同初相位以及不同的初相位差[1,2]等的信号源条件下，呈现出不同的李萨如图像，如图1所示。学生根据现有教学中的方法，如切点数反比法，十字交点数反比法等，对李萨如图像进行分析，确定水平与竖直两个分振动的频率比时，存在一些局限和疑问。针对此问题，我们在总结和分析现有方法的基础上，提出一种新方法——单曲线数正比法，让学生更容易理解和掌握。

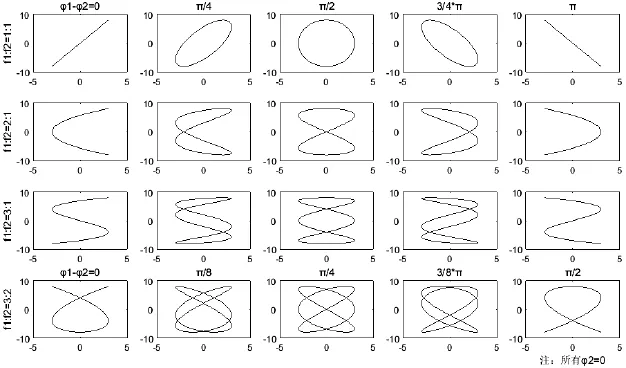
图1 常见李萨如图形

2 李萨如图形频率比的几种确定方法

2.1 切点数反比法

对于封闭的李萨如图形，我们利用切点数反比法可以很顺利得到水平与竖直振动的频率之比。即假设一封闭的李萨如图像内切一矩形。李萨如图形与矩形一水平边切点数记为Nx，与矩形一竖直边切点数为Ny，则水平振动和竖直振动的频率之比等于水平边切点数与竖直边切点数之反比，表达式为：

但是对于如图2(b)类似有端点的李萨如图形，我们无法再利用切点数反比法计算频率比。在此以水平和竖直振动频率比为3∶2的两幅典型李萨如图形为例，对以上结论做进一步说明。如图2(a)及(b)所示，李萨如图形内切于矩形ABCD。对于图2(a)，封闭李萨如图形与矩形AB边切点数为Nx=2，与BC边切点数为Ny=3，则水平与竖直方向振动频率之比为：

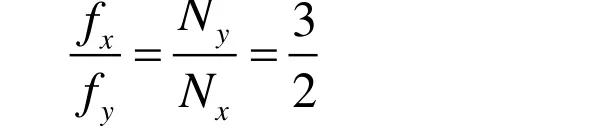
图2 切点数反比法确定频率比

即可验证封闭李萨如图形水平与竖直方向振动频率之比等于水平与竖直切点数的反比。可以简单解释如下：封闭李萨如图形与矩形水平边AB的切点数表示竖直方向的分振动完全振动次数Nx，与矩形竖直边BC的切点数代表的是水平方向分振动的全振动次数Ny。以AD边切点F，G及BC边切点E为例，在水平方向上，与切点E对应的有两条单曲线EmF，EnG。在这里，我们所说的单曲线为水平方向或竖直方向两边界上，切点与切点或切点与交点之间李萨如图像中的一段曲线。在AD和BC边之间的一条单曲线代表李萨如图形水平方向的一次半周期振动，而单曲线EmF及EnG共同代表水平方向一个来回的全振动，与BC边的3个切点即代表水平方向三次全振动，与AB边的2个切点代表竖直方向的两次全振动。因此，得到结论：水平与竖直方向分振动频率之比等于水平方向与竖直方向的切点数的反比。

但是，此类结论针对如图2(b)这类有端点李萨如图形，并不太好解释，因为不好确定切点数。因此切点数反比法适合计算封闭的李萨如图形的频率比，而不适合有端点的李萨如图形的频率比计算。

2.2 十字交点数反比法

十字交点数反比法对于封闭和有端点的李萨如图像的频率比计算都适合[3]。在前面所述的方法——切点数反比法的基础上，此方法需要再分别作一条水平和一条竖直的辅助线，即十字交叉线。假设李萨如图形的所有单曲线与水平方向的交点数为Nx，与竖直线的交点数为Ny，则水平和竖直方向分振动的频率之比等于水平与竖直交点数的反比，表达式为：

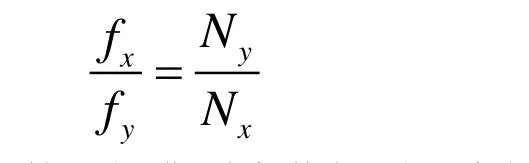
我们仍然以水平和竖直振动频率比为3:2的两幅典型李萨如图形为例，进行解释说明。如图3(a)及(b)所示，分别在图2(a)及(b)水平和竖直方向上画两条线，即十字交叉线OP和MN。先分析图3(a)图，李萨如图形与水平线OP交点数Nx=4，与竖直线MN交点数为Ny=6，因此水平与竖直方向的分振动的频率之比为：

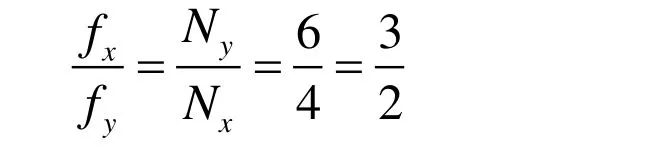
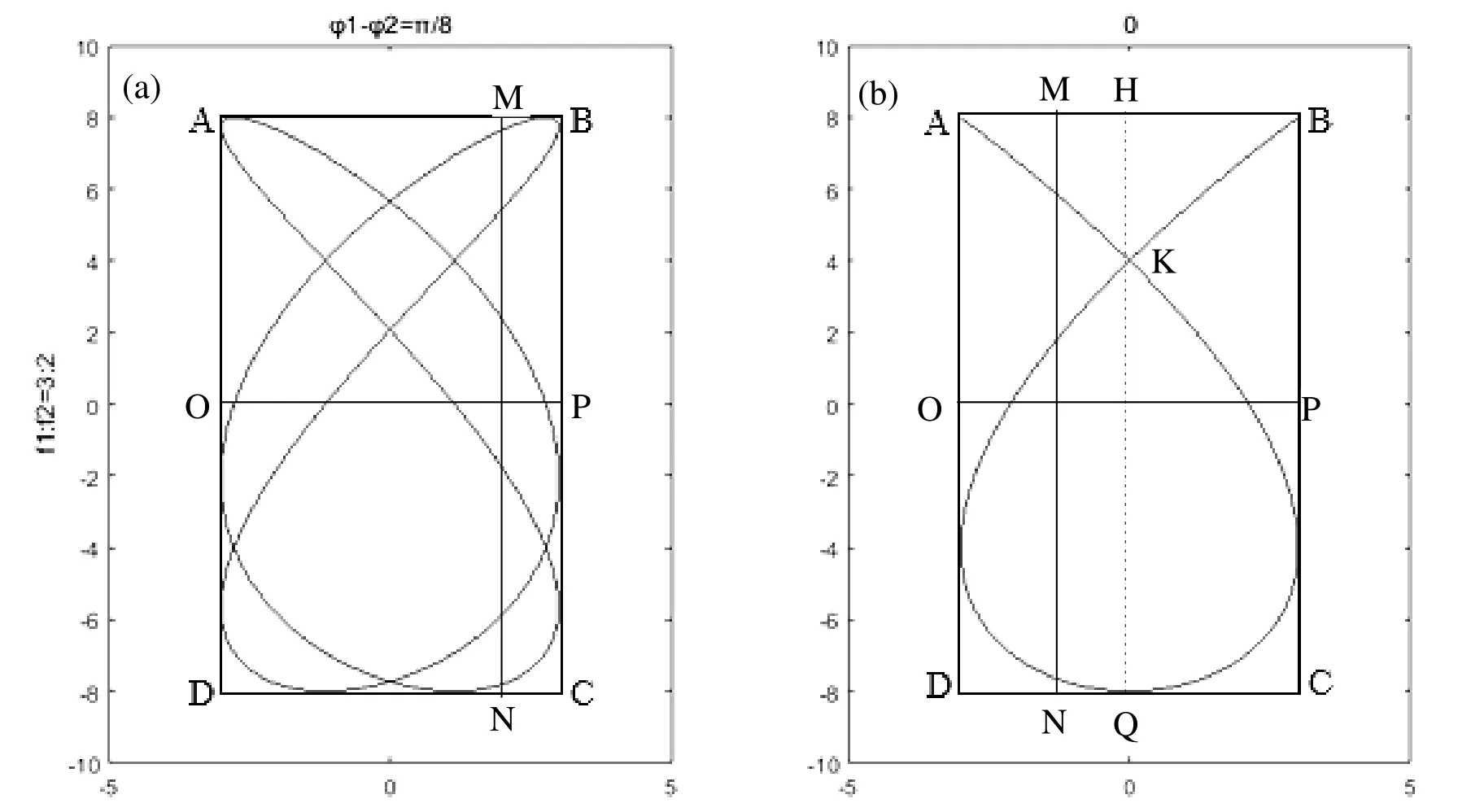
图3 十字交点数反比法确定频率比

再分析图3(b)，李萨如图形与OP交点数为Nx=2，与MN交点数为Nx=3，同理可得到水平与竖直方向的分振动频率之比为：

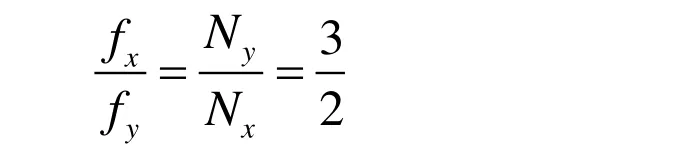
因此，水平与竖直分振动的频率之比，等于李萨如图像的单曲线分别与十字线的水平线、竖直线交点数的反比。十字线交点数反比法适用于所有封闭和有端点的稳定李萨如图形。可以解释推论如下：李萨如图像的单曲线分别与十字线中水平线交点数表示竖直方向的半周期振动次数，与竖直线交点数代表水平振动的半周期振动次数。因此我们可以得到上述结论。这里需要注意的地方是，我们强调的是单曲线（如EmF，EnG）与十字线交点的数目，因此，当十字交叉线经过李萨如自身的交点时，即两条单曲线的交点与其中一条十字线相交，如图3(b)李萨如图与虚线HQ的一个交点K，此处交点数应记为2。

但是，在大学物理教学中用十字线交点数反比法讲解，会有如下弊端：

（1）学生容易将李萨如图像的单曲线与十字线的交点数目，理解为李萨如图像与十字线的交点数目。即三线交于一点时容易出错，如图3(b)中K点。另外，当十字线处于切点处的交点也容易忽略，如图3(b)中Q点；

（2）利用这种方法讲解，学生的重点放在数交点的数目上，而非重点理解交点数目及数目比值所表示物理含义，因此即使得到错误的结论，也很少觉察错误的结果；

（3）这种方法需要作辅助线，有时李萨如图形中的线条本身就比较密集，再作辅助线使得图像更为复杂。

（4）学生在分析Nx与Ny两个数据前后以及成反比时容易弄反，而导致结果错误。

基如此，我们提出了第三种方法——单曲线数正比法，见以下内容分析。

2.3 单曲线数正比法

单曲线数正比法对于封闭和有端点的李萨如图形都适用。大学物理教学中所介绍的李萨如图形，几乎都可以内切于一个矩形。从水平方向，我们只需要计从矩形最左边AD起始点（切点或交点处）到最右边BC相应的切点或交点处截止的所有单曲线数Nx，从矩形最上边AB边起始点（即与AB的切点或交点处）到最下边DC相应切点或交点截止的所有单曲线数Ny，则水平与竖直振动频率比等于相应水平与竖直单曲线数之比，表达式为：

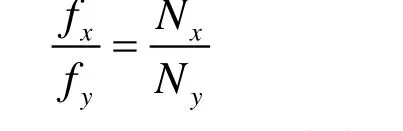
仍以频率比为3:2的李萨如图形为例，如图4(a)及(b)所示，李萨如图形与AD边切点为E、F、G，与BC边切点为H、I、J，则在水平方向上的单曲线数6条，分别为Em3I, Em4J, Fm1H, Fm6J, Gm2H, Gm5I。可解释如下：每条单曲线表示这个方向的半周期振动，单曲线数为6，则表示水平分振动的半周期振动的次数为6。同理，在同一时间里，竖直方向的半周期振动次数为4。又半周期数之比等于整周期数之比，因此，水平与竖直方向振动的频率之比为：

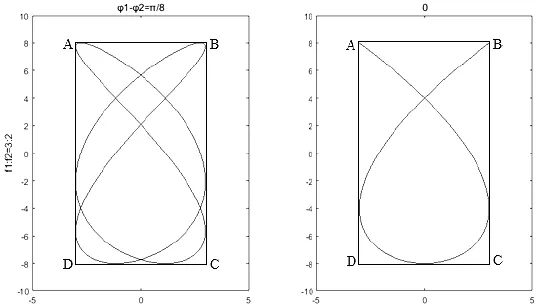
图4 单曲线数正比法确定频率比

因此，水平和竖直分振动的频率之比等于水平与竖直方向单曲线数之比。此方法对封闭和有端点李萨如图像计算两分振动的频率比都适用。相对于前两种方法，单曲线数正比法对于学生而言直观，简单，更容易理解其物理含义，甚至可以不用画任何辅助线（图4中的辅助线只为辅助说明分析），并且不容易出错，特别是频率之比等于相应方向有限长单曲线数目之比，而不是反比，大大提高学生分析正确率。

3 结论

现在大学教改正在如火如荼展开中，所学的内容增多，有些课时不得不进行大幅压缩，大学物理的教学课时同样如此，甚至是课时量对半减少。那么，如何在更少的课时，有效的传授一些知识方法，不仅需要老师在备课中对教学内容深入的钻研和仔细的甄选，同时，也要对教学的方法做进一步思考。而此方法针对相关内容的讲解，大大提高老师和学生教学过程中的成效性。因此，单曲线数正比法分析李萨如图形的频率比在课堂上推广讲解有一定积极意义。

[1] 张学文. 初相位对李萨如图形的影响分析. 湖北师范学院学报(自然科学版)[J]. 2000,20（1）: 56-60.

[2] 吉莉，刘景旺，孙光东. 用Excel测试李萨如图形实验得出的新结论. 现代物理知识[J]. 2005, 17（2）：50-52 .

[3] 杨继先. 李萨如图形的性质研究. 西华大学学报(自然科学版)[J]. 2008, 27（6），98-100.

O321

：A

：1003-7551(2016)02-0029-04

2016-05-19

湖北省教育厅科学技术研究项目（B2015031）

† 通讯作者：hewugd@163.com