基于小波神经网络的大型桥梁监测

余 颖,余 兰,彭刚跃

(1.安徽建筑大学土木学院,安徽合肥 230601;2.河海大学地球科学与工程学院,江苏南京 211100)

基于小波神经网络的大型桥梁监测

余 颖1,余 兰2,彭刚跃2

(1.安徽建筑大学土木学院,安徽合肥 230601;2.河海大学地球科学与工程学院,江苏南京 211100)

大型桥梁已成为城市交通体系关键的部分,对其进行有效地监测已势在必行。根据小波分析和神经网络在处理复杂非线性问题上的优势,将其分别应用于大型桥梁结构监测中的线形监测和应力监测这两个技术问题上。结果表明小波神经网络模型监测精度高,对桥梁的安全运营提供了技术支撑。

小波分析;神经网络;监测

当前国家经济建设发展的如火如荼,大型桥梁建设已成为国家建设的重要部分,对其进行安全监测显得尤其重要。因桥梁在运营期间随着时间推移会受到恶劣的天气、环境侵蚀、自然灾害和交通流量等外界因素影响,桥梁结构的强度和刚度会有所降低,其功能也会逐渐退化,使用寿命将会大大缩减[1,2]。如不加强监测,桥梁会受上述综合因素作用而存在安全隐患,严重时会导致桥梁倒塌现象,给人类生命财产造成极大损失[3]。对桥梁的监测是通过人工或自动手段获得多种信息对桥梁异常状态进行有效评估和综合评判,为管养人员日常养护、管理和维修提供建议[4]。一般通过温度、振动和沉降等监测参数对桥梁进行温度场监测、应力监测和线形监测。传统的监测技术存在很多弊端,如模糊和主观性不强,不能获得较好的自适应性[5]。由于传统监测手段的不足,可以利用小波神经网络对桥梁结构进行监测。小波神经网络是在小波分析理论基础上构造的一种前馈神经网络,并结合小波变换的独有时频局域化、变焦特性和传统人工神经网络自学能力,具有高智能、较强逼近能力、较高自适应能力和容错能力,成为桥梁监测的有效方法。

1 小波神经网络基本理论

小波神经网络前置预处理手段是将输入的特征向量根据小波分析的数学理论对其进行预处理。该多层前向网络是需对权值进行训练的一种非线性可微函数网络并且需基于误差反向传播此算法[6]。小波神经网络模型含输入层、隐含层和输出层且呈现拓扑结构,结构如图1所示。并要使用小波函数替代隐含层函数,其中的输入层和隐含层之间的权值、阈值分别由小波基函数的尺度、平移参数代替[6]。

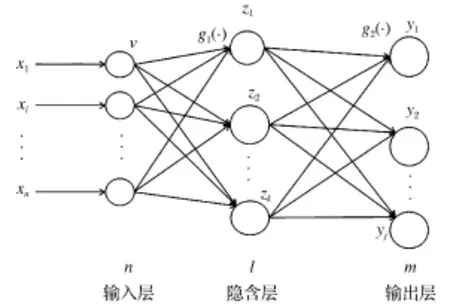
图1 小波神经网络模型Fig.1 Wavelet neural network model

在图1中,x代指小波神经网络的输入层中输入向量,x＝{xi|i＝1,2,…,n};y代指小波神经网络的输出层中输出向量,y＝{yi|i＝1,2,…,m};l、m、n分别代表隐含层、输出层和输入层各节点的数量;g1(·)为隐含层传递函数;g2(·)为输出层的传递函数。

小波神经网络理论表达式为[7]

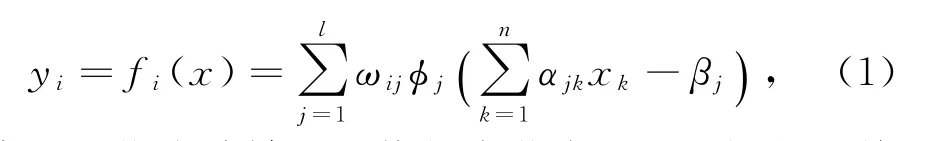
其中:ωij指小波神经网络相应节点i和j间的连接权值;ϕj为小波神经网络隐含层节点j的小波基函数;αjk和βj分别代指小波基函数的伸缩系数和平移系数;下标i、j、k分别表示输入层、输出层和隐含层各节点。

对于隐含层小波神经元的激励函数选用墨西哥草帽小波函数,即

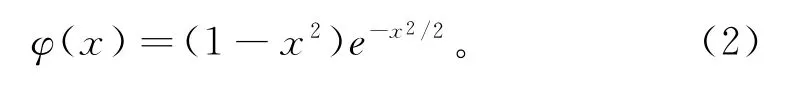
2 小波神经网络训练算法

为提高小波神经网络在桥梁健康监测的应用,减少所需时间,提升小波神经网络中的参数训练能力,将梯度下降法和递推最小二乘法引入到小波神经网络的训练中[8],其数学表达式为

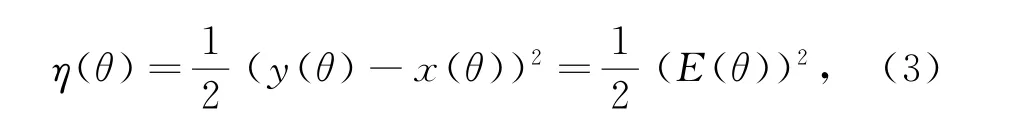
其中:E(θ)是输出误差。

2.1 小波神经网络权重的训练

因为小波神经网络的输出和权重之间存在着线性关系,所以可采用最小二乘法计算。对小波神经网络的权值系数用最小二乘法训练,能保证模型控制响应的实时性,同时避免陷入局部最优解,而且无需进行矩阵的求导计算,所采用的递推最小二乘法的公式为[8]

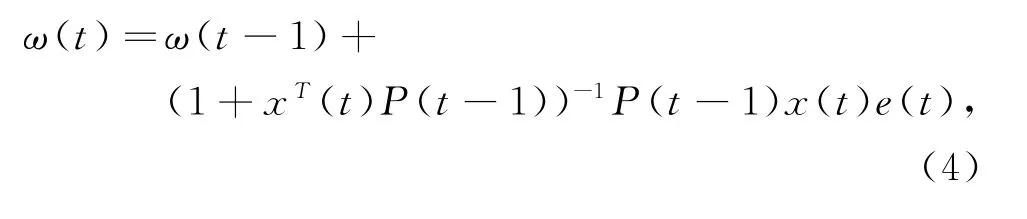
其中:P(t－1)＝(x(t－1)xT(t－1))－1;x(t)＝[ϕ1(t),ϕ2(t),…,ϕn(t)],这里x(t)是神经网络隐含层的输出。

2.2 平移和伸缩参数的设置

对小波神经网络训练中的伸缩和平移参数加入动量项,以此平滑权重大小,加快模型收敛速度,提高动态性。训练伸缩系数αjk和平移系数βj用梯度下降法,可避免陷入局部最小值,其相应的训练算法为

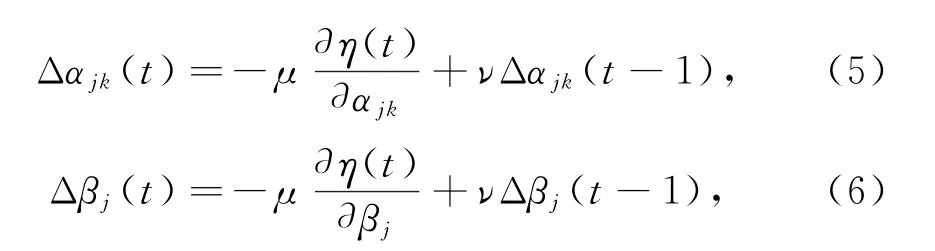
其中:μ是训练率;ν是动量系数。

3 实例分析

以安徽蚌埠大庆路淮河公路桥桥梁监测为例,桥梁全长1 778 m,主桥的桥型是三跨连续半漂浮体系的自锚式悬索桥,主桥跨径组合为(80＋200＋80)m。全桥布置成为双向六车道,全宽41.5 m,共布置桥面达到40.5 m。选择训练样本时只选取了该桥梁部分吊点实测数据,同时要用递推最小二乘法和梯度下降法去训练小波神经网络,训练时采用样本逐步积累,将后面实测后的样本加入训练样本里,这样训练出来的结果精度更高。算法用MATLAB软件编制,其参数设置是μ＝0.03,ν＝0.25,算法允许的误差为0.001。并利用神经网络模型[9]监测那些吊点,以此和小波神经网络模型的监测结果做比较。

为验证小波神经网络模型监测成桥后部分吊点线形的有效性,利用实测数据的样本进行仿真训练,相应的成桥后部分吊点线形监测结果如表1所列。

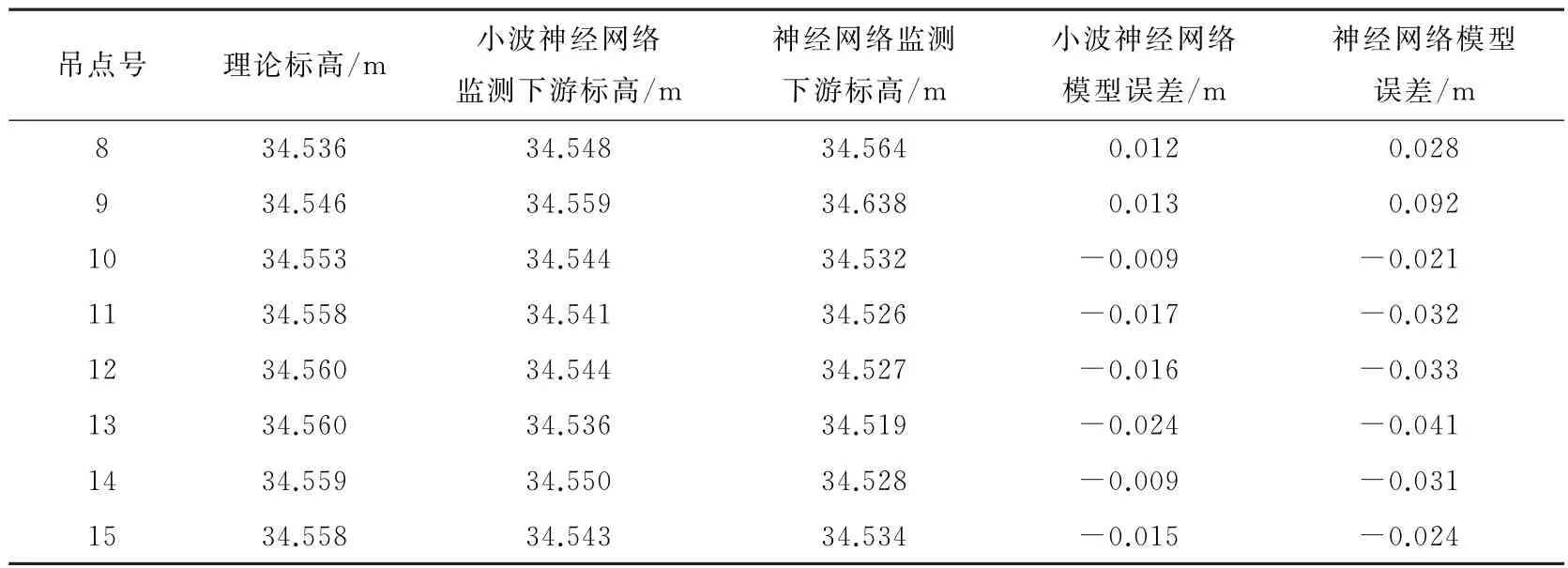
表1 成桥后部分吊点线形监测结果Table 1 Part of the lifting point of linear monitoring results

从表1可看出,小波神经网络模型监测的最大误差是24 mm,最小误差是9 mm,其他大部分误差在15 mm左右,神经网络模型监测的最大误差是92 mm,最小误差是21 mm,其他大部分误差在30 mm左右。显然,小波神经网络模型相对神经网络模型的监测效果较好,误差都在允许误差范围之内。

以上只是验证小波神经网络和神经网络对成桥后部分吊点的线形监测,明显小波神经网络模型监测效果较好。因此选用小波神经网络模型监测成桥后的主梁线形,主梁线形如图2所示。

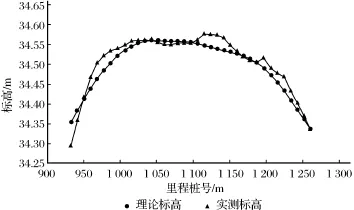
图2 主梁线形Fig.2 Girder linear

从图2可以看到,桥主梁线形监测精度较高,直观显现出实测标高和理论标高很接近。于是以小波神经网络模型来监测第四联主桥的上下缘,监测主梁受力是否正常,其断面应力监测结果见表2。从表2可以看出,LS10断面上缘应力和下缘应力监测理论值和实测值基本吻合,主梁结构受力正常,表示小波神经网络模型监测的效果比较好。

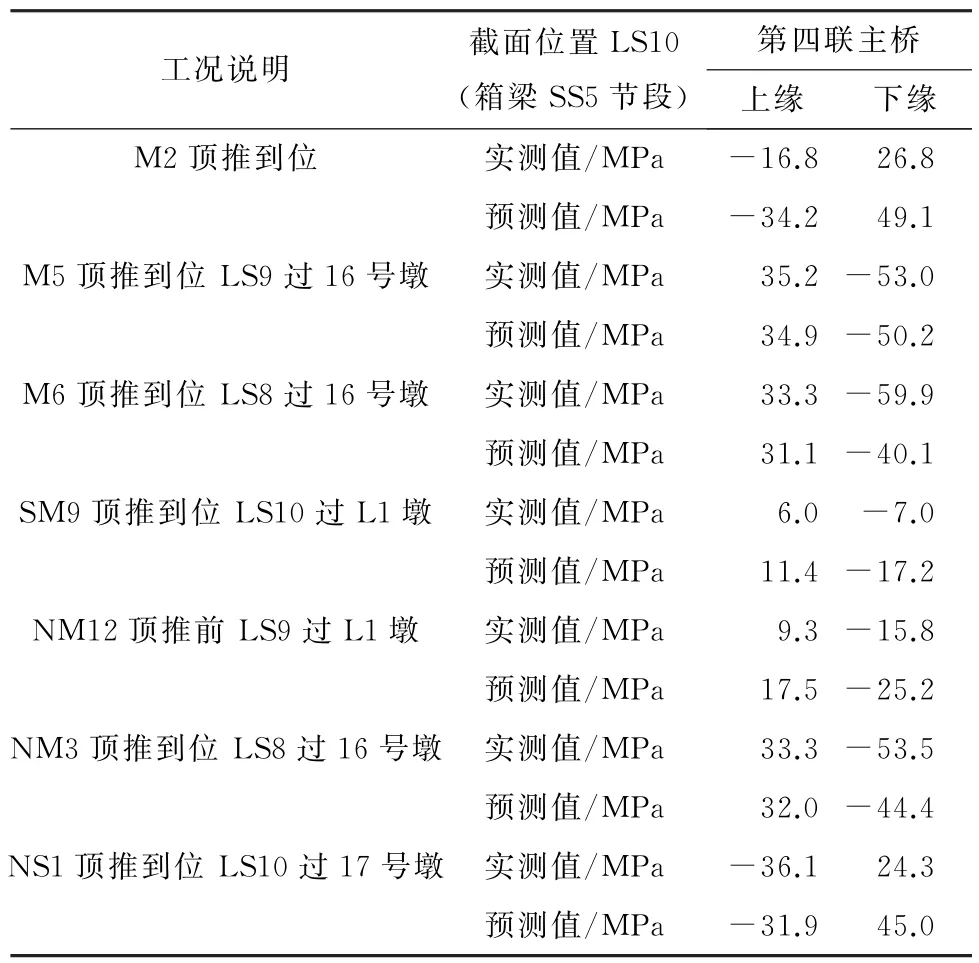
表2 LS10断面应力监测结果Table 2 LS fracture surface stress monitoring result

4 结论

以安徽蚌埠大庆路淮河公路桥桥梁监测为例,对其利用递推最小二乘法和梯度下降法训练此小波神经网络,同神经网络一起进行监测,结果表明小波神经网络模型监测精度较神经网络监测精度高。分析主梁线形的实测标高和理论标高,两条线比较接近,突出小波神经网络模型精度高的优势,并将其应用在应力监测中。应力监测结果表明主梁结构受力正常,可以用作评判桥梁健康状态。实例中用小波神经网络模型监测桥梁的线形和应力的精度较高,可以用来作为养护专家对桥梁进行安全性评价,可行性好,有较好的应用前景。

[1] 缪长青,韩惠婷,李爱群,等.江阴大桥原结构安全监测系统设计分析[J].公路交通科技,2007,24(11):81-86,91.

[2] 何浩祥,闰维明,马华,等.结构健康监测系统设计标准化评述与展望[J].地震工程与工程振动,2008,28(4):154-160.

[3] 乐志平.桥梁运营期监测系统研究现状与应用进展[J].山西建筑,2008,34(15):328-329.

[4] 袁万城,崔飞,张启伟.桥梁健康监测与状态评估的研究现状与发展[J].同济大学学报:自然科学版,1999,27(2):184-188.

[5] 李宏男,高东伟,伊廷华.土木工程结构健康监测系统的研究状况与进展[J].力学进展,2008,38(2):151-166.

[6] 关顺,王振伟,张黎.改进遗传神经网络对露天矿边坡位移预测[J].辽宁工程技术大学学报:自然科学版,2015,34(5):618-622.

[7] 陈世立,陈新民.改进BP神经网络在冲压发动机性能预测中的应用[J].导弹与航天运载技术,2007,36(3):46-49.

[8] 黄舜杰.基于小波神经网络的桥梁健康监测研究[J].计算机与现代化,2013,29(6):44-47.

[9] 杨学超,何彩平.基于BP人工神经网络的路基压实度预测模型研究[J].甘肃科学学报,2011,23(3):132-135.

Large-scale Bridge Monitoring on Basis of Wavelet Neural Network

Yu Ying1,Yu Lan2,Peng Gangyue2
(1.Civil Engineering,Anhui Jianzhu University,Hefei230601,China; 2.School of Earth Sciences and Engineering,Hohai University,Nanjing211100,China)

It is imperative to monitor large-scale bridge which has been the key part of urban traffic system.Based on the advantage of wavelet analysis and neural network when dealing with complex nonlinear problems,they are used in linear monitoring and stress monitoring in large-scale bridge structure.The result shows that wavelet neural network model has high monitoring precision so it can offer technical support for safety operation.

Wavelet analysis;Neural network;Monitor

TM183

:A

:1004-0366(2016)05-0075-04

2016-04-01;

:2016-05-20.

余颖(1990-),女,安徽安庆人,硕士研究生,研究方向为结构工程.E-mail:hohaiyulan＠163.com.

Yu Ying,Yu Lan,Peng Gangyue.Large-scale Bridge Monitoring on Basis of Wavelet Neural Network [J].Journal of Gansu Sciences,2016,28(5):75-78.[余颖,余兰,彭刚跃.基于小波神经网络的大型桥梁监测[J].甘肃科学学报,2016,28(5):75-78.]

10.16468/j.cnkii.ssn1004-0366.2016.05.018.