层合板在横向激励和温度作用下的动力响应

杨静宁,谭 杰,邱 平

(兰州理工大学理学院,甘肃兰州 730050)

层合板在横向激励和温度作用下的动力响应

杨静宁,谭 杰,邱 平

(兰州理工大学理学院,甘肃兰州 730050)

以受横向激励载荷和温度荷载共同作用下的复合材料层合板为研究对象,采用Von Kármán非线性理论和层合板理论,建立了非线性动力学的偏微分控制方程。通过Galerkin方法进行单模态离散并采用摄动法对其进行数值分析,得到了温度、激励荷载、铺设方式对层合板振动响应幅频的影响关系。

层合板;热应力;几何非线性;振动;摄动法

近年来,国内外学者对层合板的动力学问题进行了广泛研究。Gupta A K等[1]研究了温度在板厚成线性变换或者在x轴和y轴上成抛物线变换的正交矩形板的振动影响。Sharma S K[2]在经典理论基础上对粘弹性正交各向异性矩形板在变温环境下的自由振动进行了分析研究。Ducceschi M等[3]运用带有艾里应力函数和横向位移的方程加入冯卡门非线性项对矩形板在自由振动与受迫振动模态交互下的非线性振动问题进行了相关研究。赵龙胜等[4]采用了分层理论对复合层合板四边简支条件下的模态振型及其固有频率进行了理论研究和相应的实验分析。陈富军等[5]基于局部移动Kriging无网格法对层合板自由振动进行了分析。研究基于经典理论引入Von Kármán几何非线性项对复合材料层合板在横向激励和温度共同作用下的非线性振动进行了分析,建立了正交各向异性层合板的非线性动力学控制方程,采用Galerkin法对其进行一阶离散,并运用摄动法进行数值求解,讨论温度、激励荷载、铺设方式对层合板振动响应幅频的影响。

1 控制方程

受横向简谐载荷和热载荷共同作用下的层合板模型如图1所示。坐标轴位于板中面边缘位置,坐标(x,y,z)代表板中任意一点的位置。a、b、h分别代表板的长、宽和高。

图1 层合板几何模型Fig.1 Geometric model of laminate

用Von Kármán非线性理论和层合板理论,可得用位移表示的非线性控制方程:

其中:Qij为刚度系数;αk(k＝x,y)表示为x,y方向的热膨胀系数。

2 单模态离散

选取满足四边简支边界条件的线性振动函数表达式为

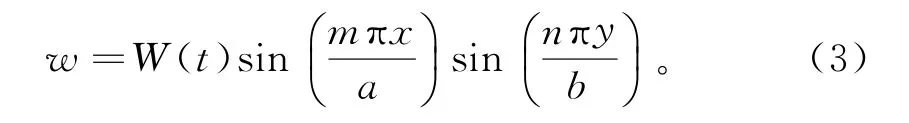
设层合板内满足边界约束条件的u,v方向位移的表达式为

将式(3)与式(4)的3个位移的表达式代入非线性动力学偏微分控制方程(1)中第三式,并利用Galerkin方法进行单模态离散,可得非线性动力学方程

其中:

采用摄动法L-P法对方程(5)进行研究分析,引入小参数ε,并且设α＝εα,p＝εp,τ＝Ωt,对外载荷频率Ω和解W(τ)进行幂级数展开,并将小参数ε的同次幂的项合在一起,可得方程

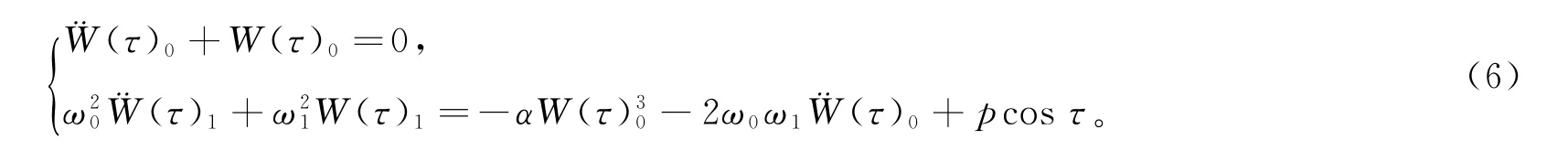
方程(6)第一式的近似解可写为

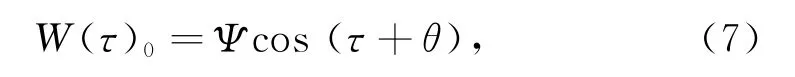
其中:Ψ表示层合板的响应幅值,将W(τ)0解的表达式(7)代入到方程(6)第二式中,并运用三角函数关系

可得

消去式(9)中的久期项,则可得层合板振动的频率、幅值和激励载荷三者之间的关系为

3 数值计算及结果分析

基于层合板振动的频率、幅值和激励载荷的关系,以石墨纤维材料为例,采用数值方法对经典理论下的层合方板在横向激励和温度作用下的非线性动力学问题进行分析。

复合层合方板在只受温度效应作用下的振动幅值与频率比的关系如图2所示。由图2可以看出,相同频率比时,随着温度的升高,会使自由振动的幅值变小。相反,在相同的振动幅值时,随着温度的升高,频率比相应略微地变高。

图2 不同温度对层合方板自由振动幅频曲线的影响Fig.2 The effect of different temperature on laminate free vibration amplitude-frequency curve

在一定温度(ΔT＝100)下,不同铺层方式对层合方板的自由振动的振动幅值和频率的比值关系如图3所示。当角铺设方式为[0,90,90,0]和[0,90,0,90]时其幅频曲线关系完全相同且略高于铺设方式为[0,0,0,0]的幅频曲线,角铺设为[0,30, 90,－30]时的幅频曲线接近于[0,45,90,－45]的幅频曲线。则在相同振幅幅值的情况下,角铺设为[0, 45,90,－45]时的响应频率最小。

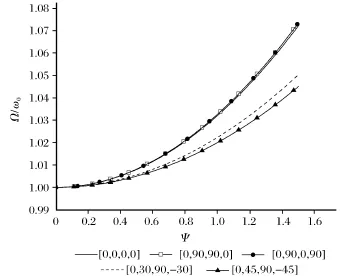
图3 不同角铺设对层合板幅频曲线的影响(ΔT＝100)Fig.3 The effect of laying from different angle on laminate amplitude-frequency curve(ΔT＝100)

激励载荷幅值系数为q＝1 000时在不同温度效应作用下,激励载荷频率Ω与基频ω0的比值对层合方板动态响应幅值Ψ的影响如图4所示。当温度升高时,层合方板的响应幅值既有增大也有减小,并非单一的递增递减变化。而且随着温度的升高,方板振动的不稳定区域增加。

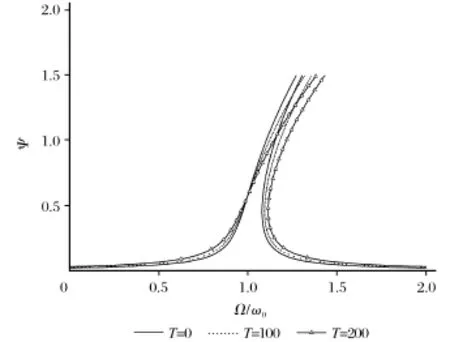
图4 热-机载荷对层合方板的幅频曲线的影响(q＝1 000)Fig.4 The effect of thermal-machine load on laminate amplitude-frequency curve(q＝1 000)

在同一温度(ΔT＝100)和同一激励载荷幅值系数(q＝1 000)下,不同的角铺设方式对层合方板的振动特性的影响如图5所示。由图5可以看出,相同厚度的层合板,通过改变角铺设方式,系统的振幅曲线出现了交叉现象。

4 结论

以受横向激励载荷和温度荷载共同作用下的复合材料层合板为研究对象,建立了层合板的非线性动力学偏微分控制方程。采用Galerkin方法进行单模态离散,并用摄动法对其进行分析计算,以石墨纤维材料制成的层合方板为例,得到了如下结果:

图5 角铺设对层合方板的振动特性的影响(ΔT＝100,q＝1 000)Fig.5 The effect of laying from different angle on laminate amplitude-frequency curve(ΔT＝100,q＝1 000)

(1)在不考虑横向激励载荷的情况下,相同频率比时,随着温度的升高,使自由振动的幅值变小;

(2)在一定温度及相同振幅幅值的情况下,角铺设为[0,45,90,－45]时的响应频率最小; (3)当温度升高时,方板振动的不稳定区域增加; (4)通过改变角铺设方式,系统的振幅曲线会出现交叉现象。

[1] Gupta A K,Kumar S.Thermal Effect on Vibration of Orthotropic Rectangular Plate with Thickness Variation as Linearly and Parabolically in x-and y-Directions Respectively[J].International Journal of Mathematical Sciences and Applications, 2013,38(2):32-35.

[2] Sharma S K.Free Mechanical Vibrations of Visco-Elastic Orthotropic Rectangular Plate with Exponential Varying Temperature[J].International Journal of Engineering Sciences and Research technology,2014,53(1):54-59.

[3] Ducceschi M,TouzéC,Bilbao S,et al.Nonlinear Dynamics of Rectangular Plates:Investigation of Modal Interaction in Free and Forced Vibrations[J].Acta Mechanica,2014,225(1):213-232.

[4] 赵龙胜,吴锦武,赵飞,等.复合材料简支板固有频率与振型分析[J].南昌航空大学学报:自然科学版,2013,27(2):10-17.

[5] 陈富军,魏春志,姚林泉.基于局部移动Kriging无网格方法的层合板自由振动分析[J].计算力学学报,2013,30(4):559-564.

[6] 杨静宁,甘文艳,邱平.变厚度夹层环形板大挠度问题的打靶法求解[J].甘肃科学学报,2010,22(2):106-109.

[7] 杨静宁,武俊,高秀娟.热环境下夹层矩形板非线性问题的数值解[J].甘肃科学学报,2013,25(4):8-11.

[8] 赵龙胜,宋福英.复合材料层合板振动特性的模态实验研究[J],材料导报,2015,29(S1):98-101.

Dynamic Response of Laminate under Horizontal Incentive and Temperature Action

Yang Jingning,Tan Jie,Qiu Ping
(School of Sciences,Lanzhou University of Technology,Lanzhou730050,China)

The laminate subjected to horizontal incentive load and temperature load is taken as researching object,and Von Kármán nonlinear theory and laminate theory are adopted,as a result,derivative control equation of non-linear dynamics is built.By conducting single mode disperse with Galerkin and analyzing its value with perturbation method,the relationship curve of temperature,stimulating load,laying mode to vibration response amplitude frequency of laminate is attained.

Laminate;Thermal stress;Geometric nonlinearity;Vibration;Perturbation method

O343

:A

:1004-0366(2016)05-0030-04

2015-12-30;

:2016-03-01.

甘肃省自然科学基金项目(2011GS04154).

杨静宁(1969-),男,副教授,硕士生导师,研究方向为复合材料结构的非线性力学行为.E-mail:yangjn＠lut.cn.

谭杰.E-mail:jack664062death＠163.com.

Yang Jingning,Tan Jie,Qiu Ping.Dynamic Response of Laminate under Horizontal Incentive and Temperature Action[J].Journal of Gansu Sciences,2016,28(5):30-33.[杨静宁,谭杰,邱平.层合板在横向激励和温度作用下的动力响应[J].甘肃科学学报,2016,28(5):30-33.]

10.16468/j.cnkii.ssn1004-0366.2016.05.008.