抽象空间脉冲发展方程初值问题的上下解方法

李 莹

(宝鸡文理学院数学与信息科学学院,陕西宝鸡 721013)

抽象空间脉冲发展方程初值问题的上下解方法

李 莹

(宝鸡文理学院数学与信息科学学院,陕西宝鸡 721013)

主要研究有序Banach空间中一阶脉冲发展方程的初值问题解的存在性。仅在半群为正半群时,对脉冲项加很少限制,利用正算子半群特征与上、下解单调迭代方法,得到了非线性脉冲发展方程初值问题最小、最大mild解的存在性等若干结果,推广了已有工作。

上下解;Mild解;初值问题;正C0-半群;单调迭代方法

研究有序Banach空间X中含脉冲发展方程的初值问题

解的存在性。其中A为X中的稠定闭算子,f(t,x)∶J×X→X连续,J＝[0,T],0＝t0＜t1＜…＜tm＜tm＋1＝T。初值x0∈X。脉冲函数Ik∶X→X(k＝1,2,…,m)。分别表示u(t)在t＝tk处的左极限与右极限(k＝1,2,…,m)。

将上下解单调迭代方法应用于不含脉冲的发展方程初值问题

已有很多结果,见参考文献[1-5]。如文献[3]中在上、下ω-解存在的情形下,获得了非脉冲发展方程(2)最小及最大mildω-周期解的存在性。但这些文献研究的都是不含脉冲项的一般抽象发展方程。将上下解方法应用于含脉冲的发展方程的相关文献比较少,并且大多是在紧半群或等度连续半群的条件下获得的,见文献[6-13]。

假设-A生成的半群为正半群,在上、下解都存在的情形下,采用单调迭代方法,得到了含脉冲的发展方程(1)最小、最大mild解的存在性,并且最小、最大mild解可通过上下解单调迭代求解,在这一过程中,仅要求脉冲函数连续及单调;若只要求mild解的存在性,还可将脉冲函数的条件减弱,只限制其单调性。同时在证明中可以看出:对非脉冲发展方程(2),即便不要求T(t)等度连续,同样可得到最小、最大mild解的存在性等结果,削弱了定理条件,得到的结果也是新的。

1 预备工作

设X为有序Banach空间,P为X中的正元锥,则可由P引出X中的序关系“≤”:x≤y⇔y－x∈P。令J＝[0,T],记PC(J,X)＝{u∶J→X∣u(t)在J′上连续,在每个tk点左连续、右极限存在,(k＝1, 2,…,m),其中J′＝J{t1,t2,…,tm}。令J0＝[0,t1],J1＝(t1,t2],…,Jm＝(tm,T]。在有限区间上,易见PC(J,X)按凸锥＝{u∈PC(J,X)∶u(t)≥0,t∈J}导出的序也构成有序Banach空间,且亦为正规锥。对∀v,w∈PC(J,X),当v≤w时,记[v,w]为PC(J,X)中的序区间。

在后面的讨论中,需要利用线性发展方程

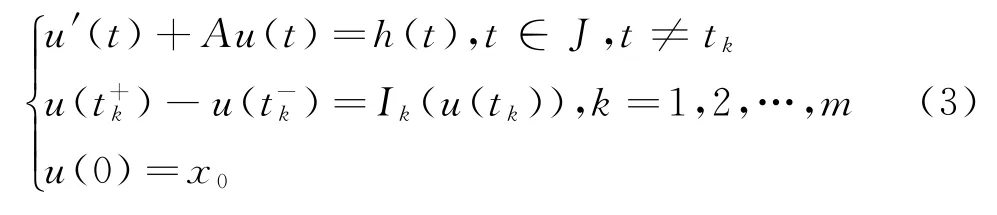
的相关结论。先看一个引理。

引理1 对∀x0∈D(A),Ik∶D(A)→D(A)(k＝1,2,…,m),h(t)∈PC(J,X)∩C1(J′,X),问题(3)存在唯一古典解:

u(t)∈PC(J,X1)∩C1(J′,X)∩C(J′,X1),且此解表示如下:

证明由文献[1]中非脉冲情形的结果知:在每个Ji(i＝0,1,…,m)上问题(3)存在唯一古典解ui(t)∈C1(Ji,X)∩C(Ji,X1)(i＝0,1,…,m),且可表示如下:

构造函数u(t)如下:

显然

u(t)∈PC(J,X1)∩C1(J′,X)∩C(J′,X1),满足问题(3)。故又由uk(t)(k＝1,2,…,m)的唯一性知,问题(3)存在唯一古典解:

u(t)∈PC(J,X1)∩C1(J′,X)∩C(J′,X1),且此解表示如下:

命题得证。

而对∀x0∈X及h∈PC(J,X),Ik∶X→X(k＝1,2,…,m),引理1确定的式(4)不一定可微,仅有u(t)∈PC(J,X),是问题(3)的mild解。

同样地,对Banach空间X中的非线性脉冲发展方程初值问题(1)有类似的结果。

引理2 设-A为C0-半群T(t)(t≥0)的无穷小生成元,C为一实数,则u(t)∈PC(J,X)为方程(1)的mild解的充要条件是u(t)满足积分方程:

其中:S(t)＝e－CtT(t)(t≥0)为－(A＋CI)生成的C0-半群。

对于上、下解有如下定义。

定义1 若v∈PC(J,X1)∩C1(J′,X)∩C(J′,X1)满足[4]:

则称v为脉冲发展方程(1)的上解;不等式全取反向时,称为下解。

2 主要结果

对于J＝[0,T],PC(J,X)构成有序Banach空间,故可以在整个区间上考虑初值问题(1)mild解的存在性[14],得到如下定理。

定理1-A生成正C0-半群T(t),x0∈X,Ik∶X→X(k＝1,2,…,m)连续。若问题(1)存在下解v0及上解w0,使v0≤w0,且满足如下假设:

(H1) ∃C≥0,对∀x1,x2∈X,t∈J,当v0(t)≤x1≤x2≤w0(t)时,有

(H2) 对∀x1,x2∈X,当v0(tk)≤x1≤x2≤w0(tk)(k＝1,2,…,m)时,有

(H3) ∃L＞0,使得对任意的单调序列B＝{un}⊂[v0,w0],有

则初值问题(1)在[v0,w0]中存在最小mild解u和最大mild解,并且和分别可用上、下解单调迭代求解。

证明记D＝[v0,w0],S(t)＝e－CtT(t)(t≥0)为－(A＋CI)生成的正C0-半群。令

对∀h∈D,考虑X中的线性脉冲发展方程初值问题:

由引理1,问题(6)存在唯一的mild解:

由Ik(k＝1,2,…,m)的连续性,易见Q∶D→PC(J,X)连续。若u∈D为Q的不动点:u＝Qu,u满足积分方程(5)。则由引理2知,u为问题(1)的mild解,反之则不是问题(1)的mild解。故问题(1)的mild解即为Q的不动点。

对∀h1,h2∈D,h1≤h2,由假设(H1)和(H2),有

即Qh1≤Qh2,故Q∶D→PC(J,X)为增算子。

下证:v0≤Qv0,Qw0≤w0。

因为v0为方程(1)的下解,故h(t)＝v′0(t)＋Av0(t)＋Cv0(t)∈PC(J,X),且h(t)≤f(t,v0(t))＋Cv0(t)。由线性脉冲发展方程mild解的积分表示,有

又因为I1∶X→X连续,B0(t1)是X中的相对紧集,所以α(I1(B0(t1)))＝0。故

由Bellman不等式,α(B(t))≡0,t∈J1(特别地,α(B(t2))＝0),所以对∀t∈J1,{vn(t)}相对紧。

类似地可以证明,对∀t∈Jk(k＝2,3,…,m),α(B(t))≡0,从而{vn(t)}相对紧。因此,对∀t∈J,{vn(t)}相对紧。结合单调性,{vn(t)}处处收敛,即{vn(t)}→¯u(t)于t∈J。同理{wn(t)}→¯u(t)于t∈J。

因为{vn(t)}∈PC(J,X),所以在每个Jk(k＝2,3,…,m)上有界可积。又因为t∈Jk时,vn(t)＝(Qvn－1)(t)＝S(t)x0＋

令n→∞,由Lebesgue控制收敛定理,对∀t∈Jk(k＝2,3,…,m),有

注:即使对于不含脉冲的发展方程(2),上述定理的结论也是新的,不要求T(t)的等度连续性。

如果分别在每个Ji(i＝0,1,…,m)上来讨论,此时问题转化为不含脉冲的情形,因此可以不用假设脉冲函数的连续性,仍采用定理1的证明思路,仅得到了mild解的存在性。

定理2-A生成正C0-半群T(t),x0∈X,Ik∶X→X(k＝1,2,…,m)。若问题(1)存在下解v0及上解w0,使v0≤w0,且满足假设(H1)～(H3),则初值问题(1)在[v0,w0]中存在mild解。

证明略。

当P为正则锥时,结合条件(H1)和正则锥的性质可推出条件(H3)[3],这样就可删去定理1和定理2中的条件(H3),即有以下推论。

推论1 设P为正则锥,-A生成正C0-半群T(t),x0∈X,Ik∶X→X(k＝1,2,…,m)连续。若问题(1)存在下解v0及上解w0,使v0≤w0,且满足假设(H1)和(H2),则初值问题(1)在[v0,w0]中存在最小mild解和最大mild解,并且和分别可用上下解单调迭代求解。

推论2 设P为正则锥,-A生成正C0-半群T(t),x0∈X,Ik∶X→X(k＝1,2,…,m)。若问题(1)存在下解v0及上解w0,使v0≤w0,且满足假设(H1)和(H2),则初值问题(1)在[v0,w0]中存在mild解。

3 结语

不要求半群的等度连续型,仅在正C0-半群下,采用单调迭代方法,对脉冲函数附加极少限制,得到了含脉冲的发展方程(1)最小、最大mild解的存在性,并且最小、最大mild解可通过迭代求解,推广了已有工作。得到的抽象结果可应用于多种数学物理方程[17],在应用中具有一定的有效性,限于篇幅不再赘述。

[1] Pazy A.Semigroups of Linear Operators and Applications to Partial Differential Equations[M].Berlin:Springer Verlag, 1983.

[2] 李永祥.抽象半线性发展方程的正解及应用[J].数学学报, 1996,61(5):666-672.

[3] 李永祥.Banach空间半线性发展方程的周期解[J].数学学报, 1998,63(3):629-636.

[4] 李永祥.抽象半线性发展方程初值问题解的存在性[J].数学学报,2005,70(6):1 089-1 094.

[5] 李永祥.抽象半线性发展方程初值问题的整体解[J].应用泛函分析学报,2001,3(4):339-347.

[6] Chen Pengyu,Li Yongxiang.Mixed Monotone Iterative Technique for a Class of Semilinear Impulsive Evolution Equations in Banach Spaces[J].Nonlinear Analysis,2011,74:3 578-3 588.

[7] Liu J H.Nonlinear Impulsive Evolution Equations[J].Dyn.Contin.Discrete Impuls.Syst.,1999,6(1):77-85.

[8] Ahmed N U.Impulsive Evolution Equations in Infinite Dimensional Spaces[J].Dyn.Contin.Discrete Impuls.Syst.Ser.(A),2003,10:11-24.

[9] Mu Jia.Extremal Mild Solutions for Impulsive Fractional Evolution Equations with Nonlocal Initial Conditions[J].Boundary Value Problems,2012,71(1):2-12.

[10] Mu Jia,Li Yongxiang.Monotone Iterative Technique for Impulsive Fractional Evolution Equations[J].Journal of Inequalities and Applications,2011,125(1):2-12.

[11] Chen Pengyu,Mu Jia.Monotone Iterative Method for Semilinear Impulsive Evolution Equations of Mixed Type in Banach Spaces[J].Electronic Journal of Differential Equations,2010, 14:91-13.

[12] 刘燚,李莹.Banach空间脉冲发展方程整体解的存在性及其应用[J].甘肃科学学报,2014,26(5):14-19.

[13] 刘燚.无穷区间脉冲发展方程初值问题的上、下解方法[J].宝鸡文理学院学报:自然科学版,2014,34(2):10-14.

[14] 秦丽娟.Banach空间中脉冲微分方程初值问题解的存在性[J].应用数学学报,2013,36(2):249-256.

[15] 郭大钧,孙经先.非线性常微分方程泛函方法[M].济南:山东科学技术出版社,1995.

[16] Heinz H R.On the Behaviour of Measure of Noncompactness with Respect to Differention and Integration of Vector Valued Functions[J].Nonlinear Analysis,1983,7:1 351-1 371.

[17] 伍卓群,尹景学,王春明.椭圆与抛物型方程引论[M].北京:科学出版社,2003.

Upper and Lower Solutions Method of Initial-value Problem in Pulse Evolution Equation

Li Ying
(College of Mathematics and Information Science,Baoji University of Arts and Sciences,Baoji721013,China)

It is mainly study existence of initial-value problem solution in the first-order impulsive evolution equation in Banach space.Only when semigroup is positive semigroup,little limit is applied to impulsive item.By using the characteristic of positive semigroup of operators and upper and lower solutions monotonous iterative method,the existence and other some results of minimum and maximum mild solution of non-linear impulsive evolution equation initial-value problem can be attained,the current work has been popularized.

Upper and lower solutions;Mild solution;Initial-value problem;PositiveC0-semigroup;Monotonous iterative method

O175.3

:A

:1004-0366(2016)05-0005-05

2016-04-05;

:2016-05-25.

国家自然科学基金资助项目(11371031);陕西省自然科学基础研究计划资助项目(2014JM1027);宝鸡文理学院重点科研计划项目(ZK16028).

李莹(1981-),女,甘肃张掖人,硕士,讲师,研究方向为发展方程理论和应用.E-mail:chinaly1981＠163.com.

Li Ying.Upper and Lower Solutions Method of Initial-value Problem in Pulse Evolution Equation[J].Journal of Gansu Sciences,2016,28(5):5-9.[李莹.抽象空间脉冲发展方程初值问题的上下解方法[J].甘肃科学学报,2016,28(5):5-9.]

10.16468/j.cnkii.ssn1004-0366.2016.05.002.