关于树(图)的单点空间
姚 明,赵振学,姚 兵
(1.兰州石化职业技术学院,甘肃兰州 730060;2.西北师范大学数学与信息科学学院,甘肃兰州 730070)
关于树(图)的单点空间
姚 明1,赵振学1,姚 兵2
(1.兰州石化职业技术学院,甘肃兰州 730060;2.西北师范大学数学与信息科学学院,甘肃兰州 730070)
定义了全魔幻空间及优美空间、奇优美空间、单点空间,在空间中给出了互化标号的数学关系式,证明了标号互化可算法化,得到简练的运算过程和标号互化结果。
单点空间;奇优美空间;优美空间;全魔幻空间;运算关系
Golomb[1]提出以最小整点数刻划K个单位长的金属棒问题,这个问题在图论中可以用图的标号来描述。一个图G=(V,E)的优美标号是对图G的顶点分配(0,1,2,…,|E|}中的数,使得不同的顶点有不同的标号,边的标号是其2个关联顶点标号差的绝对值,使得边的标号集为(1,2,…,|E|}。Rosa猜想:所有的树都是优美树,猜想如果被证明,则Ringel-Kotzig猜想成立[2-4]。
1 预备知识
1970年,Rosa定义了图G的魔幻全标号(magical total labelings,以下记为mt):对于不为零的整数s,t和一一映射f:V(G)∪E(G)→[1,p+q],有f(x)+f(y)=s+tf(xy),称f为图G的魔幻全标号[5,6]。一些新的图标号和猜想己经引起研究者的关注[7,8]。如图G的k-魔幻标号[9,10];树的二分优美(bipartite graceful,以下记为b-g);二分奇优美(bipartite odd-graceful,以下记为b-odd)[11,12]。对于图G的一个映射f:V(G)→[0,2p-3],如果有{f(uv)|uv∈E(G)}=[1,3,…,2p-3],则称f为奇优美标号[13,14];如果图G的一个映射f:V(G)→[0,q],使得{f(uv)|uv∈E(G)}=[1,q],称f为优美标号。设N为整数,T是一棵n个顶点的二部分图:即V(T)=V1∪V2,V1∩V2=∅;V1={xi|i∈[1,s],s∈N}与V2={yj|j∈[1,t],t∈N}均为独立集。相应地,图T的拷贝T∗的顶点集二部分划分为和用一条边连接顶点u∈V(T)与顶点v∈V(T∗)后所得到的图记为H。如果图T的一个标号f对所有的u∈V1和v∈V2,总有f(u)<f(v),则称f是图T的二分标号。为叙述简便,记这种情形f(V1)<f(V2)。这类标号也被应用于其他标号的研究[15-17]。迄今为止,尽管标号的研究工作在一些特殊图类上取得了进展,但均因证明过程很少能算法化而变得困难。标号空间的定义及给定标号数学表述的应用,结果发现标号互化因证明过程可算法化而得以实施,且其简单的运算过程能够清晰表述互化结果;除此之外,还可以规模化地构造魔幻树。新方法的引入为标号的研究提供了新的数理方法,能够使得标号的研究不局限于特殊图类,也期待能够对研究优美猜想有所帮助。
若无特别声明,论及的图均指有限、无向、简单图。没有定义的术语和符号参见文献[18]。
对于整数n>m≥0,为方便叙述,记[n,m]={m,m+1,m+2,…,n}。对于偶数l>k≥0,[k,l]e={k,k+2,k+4,…,l}表示偶数集;对于奇数t>s≥1,令奇数集是[s,t]°={s,s+2,s+4,…,t}。记f(V(G))={f(x)|x∈V(G)}和f(E(G))={f(xy)|xy∈E(G)}。
定义1设(p,q)-图G有一个集合F(G)={G|G二部分图},若:
(ⅰ)对任意的G,T∈F,总有G∪T∈F;
(ⅱ)任何一个二部分图G满足G∈F,
则称F为G的二部分图空间。
定义2令N为全体整数集合。设图G∈F有一个非空点集合Γ(G),对于图G的一个标号函数f,点(f(x),f(y))∈Γ(G);若集合Γ(G)对于加法及数乘两种运算封闭,则称集合Γ(G)为G的点空间,特记P(s,t)={(s,t)|s,t∈Γ(G),s,t∈N}。
定义3令N为全体整数集合。设图G∈F有一个集合L(G)={g|g:V(G)∪E(G)→[1,p+q]}。若:
(ⅰ)对任意的g∈L(G),总存在s,t∈N,使得uv∈E(G),满足g(u)+g(v)=s+tg(uv); (ⅱ)图G的任何一个魔幻全标号满足f∈L(G),
则称L(G)为G的全魔幻空间,记为Lmt(G);称(s,t)为魔幻全标号g的魔幻常数。
定义4设集合L(G)={f|f:V(G)→[0,p-1],G∈F}。若:
(ⅰ)对任意的f∈L(G),使得uv∈E(G),满足{f(uv)|uv∈E(G)}=[1,q];
(ⅱ)图G的任何一个优美标号满足f∈L(G),
则称L(G)为G的二分优美空间,记为Lb-g(G)。
定义5如果集合L(G)={f|f:V(G)→[0,2p-3],G∈F},满足:
(ⅰ)对任意的f∈L(G),使得uv∈E(G),满{f(uv)|uv∈E(G)}=[0,2p-3]°;
(ⅱ)图G的任何一个奇优美标号满足f∈L(G),
则称L(G)为G的二分奇优美空间,记为Lb-odd(G)。
2 主要结果及证明
定理1设图H,T∈F,如果标号f∈Lmt(T),点(g(x),g(y))∈Γ(H),则标号g∈Lmt(H)。
证明由条件f∈Lmt(T),(f(xi),f(yj))∈Γ(T);相应地,标号f的拷贝f′,使得(f′(x′i),f′(y′j))∈Γ(T∗)。g为H的一个标号函数,对于边xy∈E(T)⊂E(H)和边u′v′∈E(T∗)⊂E(H),注意到点(u1,v1),(u2,v2)∈P(s,t),使得AB=C,AM=N成立,其中:

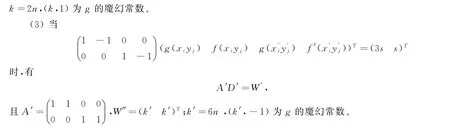
显然g(u)<g(v)。若边xy∈E(T)⊂E(H)和边u′v′∈E(T∗)⊂E(H),满足

则取边xy的对应边x′y′∈E(T∗)⊂E(H),且uv∈E(T)⊂E(H)是u′v′的对应边,使得

若(1-1)(g(xy)g(u′v′))T=(0),则αω=φ,其中:ω=(f(xiyj)f′(u′iv′j))T。
因f的拷贝为f′,所以矛盾;根据f(ytx′1)=2n,故S∪W∪{f(ytx′1)}=[1,2n-1],其中:S={f(u)|u∈V(H)},W={f(uv)|uv∈E(H-ytx′1)};f(E(H))=[1,2n-1],g∈Lmt(H)。
推论2设g∈Lmt(T);如果f∈Lmt(H),魔幻常数(k,1);则f的对偶标号f′的魔幻常数为(k′,-1),且k′=3k。
证明由定理1,有

其中:k=2n,(k,1)为f的魔幻常数。及
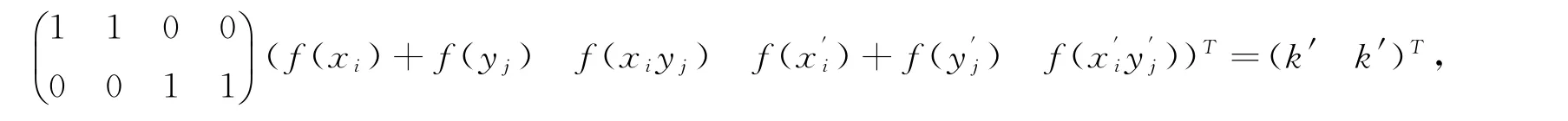
其中:k′=6n;(k′,-1)为f′的魔幻常数。所以k′=3k。
定理3设图H∈F,点(u,v)∈P(s,t)。如果g∈Lb-odd(H),则图H有标号f满足:
(ⅰ)f∈Lmt(H);(ⅱ)f∈Lb-g(G)。
证明(ⅰ)设V1={xi|i∈[1,s]},V2={yj|j∈[1,t]}。f为H的一个标号函数,注意到有点(u,v)∈P(s,t),使得
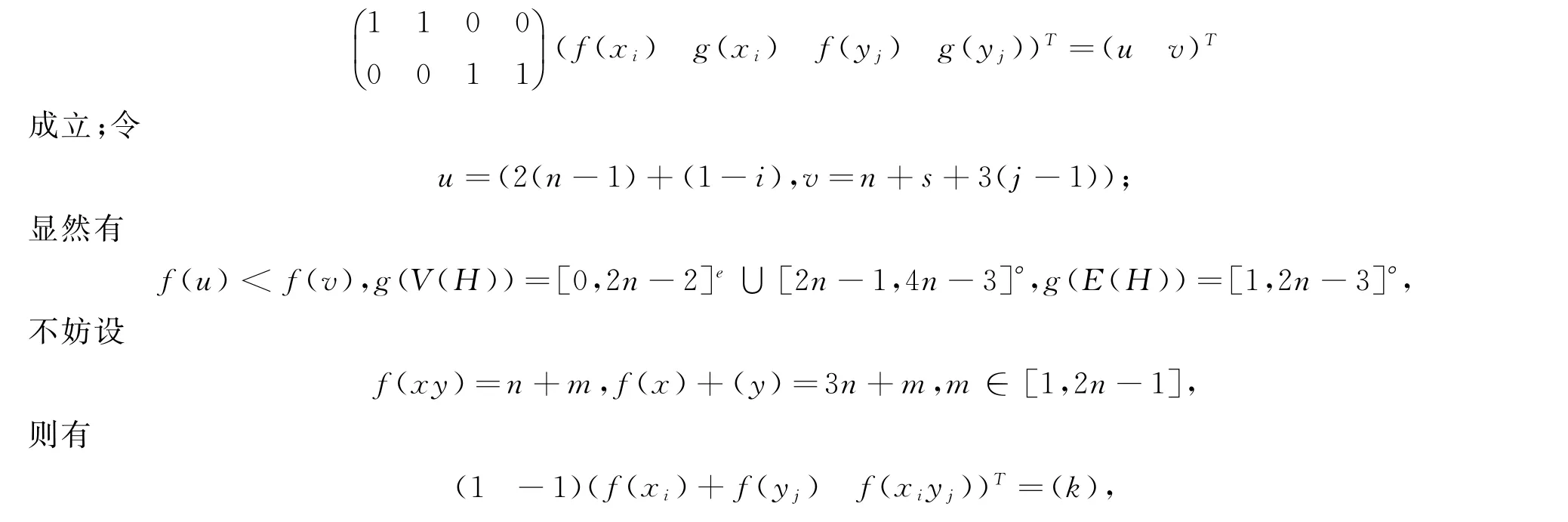
其中:k=2n,(k,1)为f的魔幻常数。证得
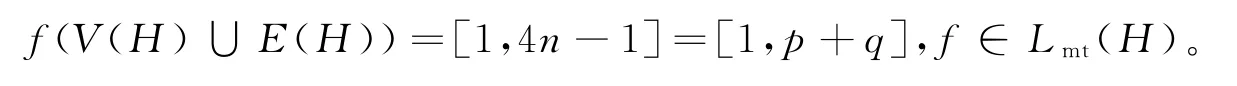
(ⅱ)令u=1+i-n,v=1-j,则有

由(ⅰ)证明有g(u)<g(v),显然f(u)<f(v),证得f(V(H))=[0,n-1]。注意到

由于g∈Lb-odd(H),g(E(H))=[1,2n-3]°,所以
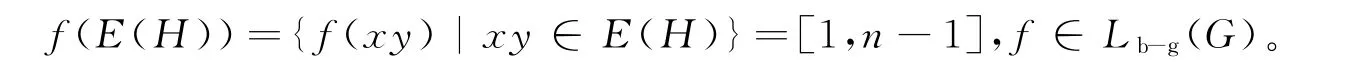
推论4如果f∈Lmt(H),则图H有h满足h∈Lb-g(G)。
证明(ⅰ)设h为H的一个标号函数,注意到有点(u,v)∈P(s,t),使得
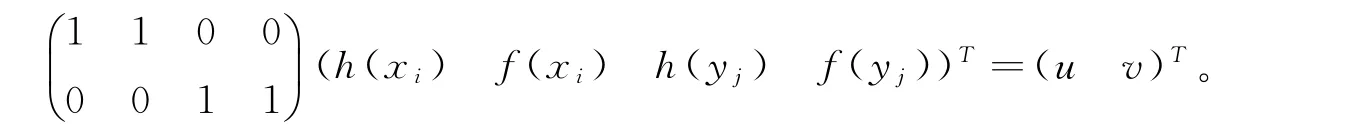
令u=n,v=n+s+2(j-1),显然有f(u)<f(v),从而h(u)<h(v),证得h(V(H))=[0,n-1]。又

由于f∈Lmt(H),f(V(H)∪E(H))=[1,p+q],所以h(E(H))={f(xy)|xy∈E(H)}=[1,n-1],h∈Lb-g(G)。
3 结语
(1)应用标号空间的定义及给定标号数学表达式,使得标号间关系的研究取得进展;其标号互化可算法化的数理关系及其简便的计算方法为研究其他未知标号提供了可借鉴的研究方法。同时看到在研究中创新方法的引入不但使证明过程简单、结果清晰,也有益于发现新结果。下步将对各种魔幻标号组建新的运算系统,尝试为标号的研究从理论上给出较佳的研究方法。
(2)问题:①如果g∈Lb-odd(H)(或f∈Lmt(H)、或f∈Lb-g(G)),则f是否为幸福(或顶点)标号?
②若H∉F,定理1、定理2是否成立?
[1] Golomb S W.How to Number a Graph.Graph Theory and Computing[M].R.C.Read ed.,New York:Academic Press,1972.
[2] Alexander Rosa.On Certain Valuations of the Vertices of a Graph[Z].New York:Gordon and Breach,1967.
[3] Gallian J A.A Dynamic Survey of Graph Labelling[J].The Electronic Journal of Combinatorics,2012,(19):6-189.
[4] Edwards M,Howard L.A Survey of Graceful Trees[J].Atlantic Electronic Journal of Mathematics,2006,(1):5-30.
[5] Yao Bing,Zhang Zhongful,Yao Ming,et al.A New Type of Magical Coloring[J].Advances in Mathmatics,2008,(37):571-583.
[6] Yao Ming,Yao Bing,Xie Jian-ming.Some Results on the K-magical Labelling of Graphs[J].Journal of Gansu Sciences,2010,(22):1-6.
[7] Kathiresan K M.Two Classes of Graceful Graphs[J].Ars Combinatoria,2000,(55):129-132.
[8] LladóA.Largest Cliques in Connected Supermagic Graphs[J].European Journal of Combinatorics,2005,(8):219-222.
[9] Yao Bing,Zhang Zhongfu,Yao Ming,et al.A New Type of Magical Coloring[J].Advances in Mathmatics,2008,(37):571-583.
[10] Albert William,Bharati Rajan.Non Super Edge Magic Total Labelling[C]//Joe Ryan,Mirka Miller.The Proceeding of the 4th International Workshop on Graph Labeling.Harbin:Harbin Engineering University and University of Ballarat,Australia,2008.
[11] Zhou Xiangqian,Yao Bing,Chen Xiang'en,et al.A Proof to the Odd-gracefulness of All Lobsters[J].Ars Combinatoria,2012,(103):13-18.
[12] Yao Bing,Cheng Hui,Yao Ming,et al.A Note on Strongly Graceful Trees[J].Ars Combinatoria,2009,(92):155-169.
[13] Gnanajothi R B.TOpics in Graph Theory[Z].Ph.D.Thesis:Madurai Kanmaraj University,1991.
[14] Liu Xinsheng,Liu Yuanyuan,Yao Bing.Odd-gracefulness of Dragon Graphs[J].Journal of Lanzhou University of Technology,2013, (39):135-139.
[15] Yao Bing,Yao Ming,Cheng Hui.On Gracefulness of Directed Trees with Short Diameters[J].Bulletin of the Malaysian Mathematical Sciences Society,2012,(35):133-146.
[16] Zhou Xiangqian,Yao Bing,Chen Xiang'en.Every Lobster is Odd-elegant[J].Information Processing Letters,2013,(113):30-33.
[17] Yao Ming,Yao Bing,Xie Jianming.Some Results on the k-magical Labelling of Graphs[J].Journal of Gansu Sciences,2010,22(1):1-6.
[18] Bondy J A,Murty U S R.Graph Theory with Application[M].New York:MaCmillan,1976.
Single Point Space of Graphs
Yao Ming1,Zhao Zhenxue1,Yao Bing2
(1.Lanzhou Petrochemical College of Vocational Technology,Lanzhou730060,China;2.College of Mathematics and Information Science,Northwest Normal University,Lanzhou730070,China)
It has defined total-magical space,graceful space,odd-graceful space and single point space in this text,in which space mathematical relationship about labeling interconversion is given,so that algorithm of labeling interconversion has been proved out,getting simple operating process and labeling interconversion result.
Single point space;Odd-graceful space;Graceful space;Total-magical space;Operating relationship
O157.5
:A
:1004-0366(2016)05-0015-05
2016-01-11;
:2016-02-19.
国家自然科学基金资助项目(61163054);甘肃省高等学校研究生导师科研项目(1216-01);甘肃省财政厅专项资金(2014-63).
姚明(1962-),男,江苏扬州人,副教授,研究方向为图的着色和标号及计算优化.E-mail:yybm918@163.com.
Yao Ming,Zhao Zhenxue,Yao Bing.Single Point Space of Graphs[J].Journal of Gansu Sciences, 2016,28(5):15-18,78.[姚明,赵振学,姚兵.关于树(图)的单点空间[J].甘肃科学学报,2016,28(5):15-18,78.]
10.16468/j.cnkii.ssn1004-0366.2016.05.004.

