基于蝙蝠算法与信号稀疏分解的DOA估计研究

冯 舒,于战海,王云汉

(1.吉林大学通信工程学院,吉林长春 130022;2.东北电力大学能源与动力工程学院,吉林长春 132012; 3.东北电力大学自动化工程学院,吉林长春 132012)

基于蝙蝠算法与信号稀疏分解的DOA估计研究

冯 舒1,于战海2,王云汉3

(1.吉林大学通信工程学院,吉林长春 130022;2.东北电力大学能源与动力工程学院,吉林长春 132012; 3.东北电力大学自动化工程学院,吉林长春 132012)

稀疏分解的DOA估计法具有很高的估计精度,但稀疏分解计算量巨大,需要较长的计算时间。针对这一问题,将蝙蝠算法与信号的稀疏分解算法相结合,应用于信号的DOA估计。利用蝙蝠搜索算法搜索路径优、寻优能力强的优点,可快速寻找到正交匹配追踪过程中每一步分解的最佳原子,从而实现信号快速稀疏分解。仿真结果表明,引入蝙蝠算法后,在有效的估计条件下,加快了计算速度,减少了计算量。

DOA算法;稀疏分解;蝙蝠算法;正交匹配追踪

波达方向(DOA,direction of arrival)估计法是典型的信号源分析手法,研究人员通过长时间的相关分析,提出了一种崭新的空间稀疏性分析法,利用信号稀疏分解做DOA估计。该方法无需获得任何先验信息,亦不需要信号阵列的高敏感性,因此十分适合求解空间最优解[1,2]。

常用的稀疏分解算法包含大量计算[3]。针对这一问题,一些研究学者将仿生智能算法应用于其中,取得了一些效果。袁志刚等[4]利用禁忌遗传和原子特性实现信号稀疏分解,但全局搜索时重建信号的效果并不明显。李越雷等[5]利用粒子群算法实现PPS信号的稀疏分解,由于粒子群算法收敛速度较慢,容易陷入局部最优解,因此计算过程中容易出现与实际情况不符的问题,这就需要对相关问题进行进一步优化[6]。

蝙蝠算法(BA,bat algorithm)由Amir等[7]于2010年首次提出,该方法属于典型的智能优化算法。基于蝙蝠算法方法简捷,求解复杂问题时优化速度快等优点,我们将蝙蝠算法应用于信号稀疏分解的DOA估计,解决稀疏分解存在的计算量大、算法速度慢、容易陷入局部最优等问题,对于多个估计,力图获得好的估计精度和收敛性能。

1 稀疏分解的DOA估计

1.1 稀疏分解的DOA估计模型

在传统阵列信号估计模型中,导向矢量矩阵的每一列ai(ω0)都对应着空间一个真实信号源[8]。将整个空间在－90°～90°的范围内按等角度划分,假设有2N＋1个信号存在于空间,如图1所示。

图1 空间信号稀疏化表示Fig.1 Space signal sparse expression

假设入射角集合{θ1,θ2,…,θ2N＋1}包含了所有可能的入射方向,导向矢量矩阵可以表示为(即相应的过完备原子库),为维的矩阵,所有入射角形成的信号集合表示为则信号的线性投影测量值为

其中:X(t)是某一时刻接收到的信号为加性噪声,显然在中,当且仅当对应的角度有信号源时sk≠0。假设空间存在K个信源,则在向量中只有K个非零值,也就是说是一个K稀疏信号。

1.2 稀疏分解的DOA估计算法应用

用稀疏分解算法来实现阵列接收信号X(t)在进行分解并得到DOA的具体数值。

信号X(t)分解为两部分,分别是aj(θj),j＝1, 2,…,2N＋1上的投影和信号的残差:

根据投影矩阵定义,投影部分可以写为

经过进一步的分析,输出信号的残差项RX将最终在原子库中实现终止过程,通过这个过程所采用的不同原子特性和具体的向量解,可以直接得到目标信号的DOA值。

2 信号稀疏分解优化

2.1 正交匹配度跟踪

作为典型的系统信号分析法,贪婪算法具有原理简单易实现、计算复杂度低、收敛速度快等特点。正交匹配追踪(OMP,orthogonal matching pursuit)算法是以匹配追踪(MP,matching pursuit)这一信号跟踪方法作为模板而推出的新方法,基本思想是在迭代过程中挑选与残差相关性最好的原子,对每一次选择的原子和对前几步选择的全部原子进行正交化处理,将挑选的原子更新到索引集,直到满足迭代条件。正交匹配算法虽然易于理解,但其每次迭代过程中对于信号位置和强度以及相应的残差计算过程都较为复杂,并且计算量较大。实际上,它每次寻找最适合原子的过程都可以看做是全局最优化问题。

将智能算法应用到OMP算法在求最优解的过程中,可以显著提升传统正交匹配追踪算法效率,并且能够对稀疏分解过程的优化和改进产生十分积极的意义。

2.2 蝙蝠算法

所谓蝙蝠算法是一类典型的样本随机优化算法,该算法将研究目标设定为样本集中的单个个体(即蝙蝠个体),通过求解整个样本集在时间和空间中的游走过程,进而获得适应于整体的随机过程的结果。

该算法的应用过程作为样本整体的空间探索过程,由单个的蝙蝠样本通过发出个体化脉冲来实现对周围环境的分析。通过使用低频但高强度的脉冲信号,蝙蝠能够快速定位猎物,即分析过程的最优解。在确定目标后,信号的频率将逐渐加大,而其强度却将逐步降低。经由具体的位置判别过程,那些与目标相比位置并不好的蝙蝠将向更有优势的位置进行移动,从而实现自身位置最优解。在整个过程中,蝙蝠发出的脉冲源的频率和强度,决定了自身整体的移动过程,而通过分析更新后的位置的特性,就能避免局部最优解的固化问题[9,10]。

2.3 基于蝙蝠算法的信号OMP稀疏分解

基于OMP信号稀疏分解的每一步,实际上是求最优解的问题。在这个过程中,原子的匹配实际上可被视作蝙蝠算法的一个近似表示法。原子特性的优劣与否,可以通过脉冲信号的残差值与过完备原子库中原子的内积的正值结果的大小来加以判断,并且优劣度与数值大小呈同方向变动。在具体的测算过程中,上述的各个变量都需要取绝对值。此处,稀疏分解效应求取最大原子的过程实际上就是蝙蝠算法的一种衍生。

基于BA-OMP稀疏分解的基本步骤:

(1)参数初始化,随机产生N只蝙蝠的初始位置γi(i＝1,2,…,n)和速度Vi、脉冲频率fi(开始时随机分配频率fi从[fmin,fmax]平均得出)在位置gγi,初始化脉冲速率ri和声音响度Ai,设置最大迭代次数max、终止阈值ε1;

(2)计算N只蝙蝠的初始位置的适应度函数值并记录最优原子的参数和最大适应度函数

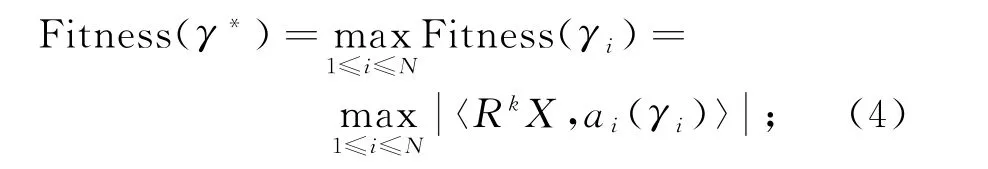
(3)单个样本优化,这一过程可通过下面所使用的调频公式进行处理,进而得到单个样本的新速度和位置解:

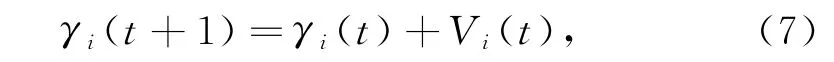
其中:β∈0,1[]是一个随机向量;

(4)局部细致分析,此处假定全集中存在一个最优解(rand＞ri),那么就可以进一步找出由随机过程而产生的局部新解

其中:ε∈－1,1[]是一个任意数字;A(t)＝＜Ai(t)＞是所有蝙蝠在这一迭代里的平均响度;

(5)如果{rand＜Ai&P(γi)＜P(γ∗)},接受这个新解,增大ri,减小Ai,脉冲速率ri和声音响度Ai的更新为

计算要素含量的最大瓶颈在于数据，本研究做了大量的数据收集和编辑整理工作。要计算2007年单位产出的资本和劳动含量，需要各行业产出、劳动投入和资本投入(包括固定资产和流动资产)等相关的数据。

其中:α和γ是常数,0＜α＜1,γ＞0;

(6)排列蝙蝠并找到当前最佳解γ∗;

(7)若达到最大迭代次数max,保存此时参数向量γ∗k＝γ∗以及最大适应度函数值Fitness(γ∗k)＝Fitness(γ∗),否则返回步骤(2);

(8)若Fitness(γ∗k)＜ε1不成立,则

并且返回步骤(1),否则算法结束。

3 实验与结果

在Matlab仿真实验平台上,考察新算法应用到DOA估计的有效性和运算速度。

基于BA-OMP算法的DOA估计如图2所示。图2中谱峰所在的位置就是空间信源的入射角度。由图2(a)可以看出在单快拍条件下,信噪比SNR＝5 dB时,经过多次实验能够有效地估计出信号DOA。图2(b)为信噪比SNR＝0时得出的仿真图,可以看出经过多次实验,该算法估计准确性比SNR＝5 dB时稍有下降,但在噪声的影响下仍能估计到DOA的值。

图2 基于BA-OMP算法的DOA估计Fig.2 DOA estimation based on BA-OMP

在上述实验条件下,分别在信噪比SNR＝－5 dB,SNR＝0,SNR＝5 dB,SNR＝10 dB时,对OMP算法和新算法做仿真实验,仿真软件为Matlab2007,计算机配置为Intel(R)2.5 GHz,2 G内存,32位操作系统。

不同算法的运行时间见表1。由表1可以看出,在信噪比不同的情况下,新算法与传统OMP算法相比具有更快的运算速度。并且当SNR＝10 dB时,新算法明显比传统的OMP算法更节省时间。蝙蝠算法优化后的正交匹配算法计算量上的减少,可以使其更早地收敛于最优解,在实际应用中可以满足实时性的要求。

表1 不同算法的运行时间Table 1 Operating time with different algorithm

4 结语

针对信号稀疏分解的DOA估计问题,引进蝙蝠算法进行优化,大大减少了算法的计算量,加快了运算速度。实验结果表明,新方法在低信噪比和小样本下依然能够得到有效结果,是解决此类复杂谱峰DOA问题的有效方法之一,蝙蝠搜索对正交匹配算法方法有着良好的优化作用,为信号稀疏分解的应用提供了参考依据,值得进一步研究。

[1] 李俊武,俞志富.改进粒子群算法在DOA估计中的应用[J].计算机工程与应用,2013,49(9):203-206.

[2] Ahmed Magdy,Mahmoud K R.Direction of Arrival Estimation Based on Maximum Likelihood Criteria Using Gravitational Search Algorithm[J].PIERS Proceedings,2013,5(6): 25-28.

[3] 刘拥军.防止过早收敛的改进型遗传算法[D].南京:河海大学,2004.

[4] 袁志刚,舒维杰,尹忠科,等.利用禁忌遗传和原子特性实现信号稀疏分解[J].计算机工程与应用,2009,45(11):142-144.

[5] 舒维杰,袁志刚,尹忠科.利用人工鱼群算法实现基于MP的信号稀疏分解[J].计算机应用研究,2009,26(1):66-67,73.

[6] 李越雷,张天骐,黄铫,等.利用粒子群算法实现PPS信号的稀疏分解[J].计算机仿真,2010,27(2):200-203.

[7]Amir Hossein Gandomi,Yang Xinshe,Amir Hossein Alavi,et al.Bat Algorithm for Constrained Optimization Tasks[J].Neural Computing and Applications,2013,22(6):1 239-1 255.

[8] Zhang Zhicheng,Shi Yaowu.Application of Artificial Bee Colony Algorithm to Maximum Likelihood DOA Estimation[J].Journal of Bionic Engineering,2013,10:100-109.

[9] Amir H Gandomi,Yang Xinshe.Chaotic Bat Algorithm[J].Journal of Computational Science,2014,5(2):224-232.

[10] 黎成.新型元启发式蝙蝠算法[J].电脑知识与技术,2010,6 (23):6 569-6 572.

DOA Estimating Study Based on Bat Algorithm and Sparse Decomposition of Signal

Feng Shu1,Yu Zhanhai2,Wang Yunhan3
(1.College of Communication Engineering,Jilin University,Changchun130022,China; 2.College of Energy and Power Engineering,Northeast Dianli University,Changchun132012,China; 3.College of Automation Engineering,Northeast Dianli University,Changchun132012,China)

DOA estimating method of sparse decomposition has very high estimated accuracy,but calculated amount of sparse decomposition is huge and need longer time.Aiming this problem,the method combining Bat algorithm and sparse decomposition in this text is used to estimate signal DOA.By the Bat algorithm＇s advantage of optimized search path and strong ability to search optimization,we can find decomposed optimizing atom in each step of orthogonal matching pursuit process with short time so that the signal can be conducted sparse decomposition quickly.The simulating result shows that calculating speed is accelerated and calculating amount is reduced under available estimating condition with Bat algorithm.

DOA algorithm;Sparse decomposition;Bat algorithm;Orthogonal matching pursuit

TN911.7

:A

:1004-0366(2016)05-0001-04

2015-12-28;

:2016-02-14.

国家自然科学基金(51075175);吉林省产业技术研究与开发项目(JF2012C013-3).

冯舒(1990-),女,吉林长春人,在读硕士,研究方向为阵列信号处理.E-mail:jiuwufz2015＠163.com.

Feng Shu,Yu Zhanhai,Wang Yunhan.DOA Estimating Study Based on Bat Algorithm and Sparse Decomposition of Signal[J].Journal of Gansu Sciences,2016,28(5):1-4.[冯舒,于战海,王云汉.基于蝙蝠算法与信号稀疏分解的DOA估计研究[J].甘肃科学学报,2016,28(5):1-4.]

10.16468/j.cnkii.ssn1004-0366.2016.05.001.