密封装置多体动力分析

马永斌,张文强,赵国文

(兰州理工大学理学院,甘肃兰州 730050)

密封装置多体动力分析

马永斌,张文强,赵国文

(兰州理工大学理学院,甘肃兰州 730050)

针对密封封装装置,采用有限元方法进行多体动力分析及密封效果的模拟,得到旋转部件的位移、弹簧的拉力变化情况以及密封压力的变化曲线。然后对结构进行柔体瞬态动力分析,得到整个密封过程中主要零部件的应力、应变等情况,以验证零件的强度和密封效果。

密封装置;瞬态动力分析;刚柔耦合;多体动力学

密封装置是储物系统的核心部件,由于工作环境比较特殊,没有足够的动力使其密封,所以会采用火攻产生压力进行密封。因而密封装置会受到比较大的冲击载荷,再加上一般来说模型尺寸不会太大,经常会出现结构失稳。如果冲击载荷太小就不能完全密封,所以对其进行动力学分析是至关重要的。目前很多企业都致力于密封装置的开发和研究,因为它对整个机构起着至关重要的作用,往往会是很难突破的一个瓶颈。

目前,对于静态结构,且作用力比较小的普遍采用橡胶O形圈进行密封,胡殿印等[1]详细论述了上下密封法兰的张开间隙、初始压缩量、密封槽口及槽底倒角半径、密封槽宽、密封圈材料、O形圈截面尺寸及工作温度等典型参数对密封性能的影响,以及运用有限元方法确定密封圈易受损和失效的关键部位和失效准则。陈志等[2]采用含高阶项Mooney-Rivlin本构模型对在机械密封沟槽中单侧受限丁腈橡胶O形圈的密封性能进行了数值计算,得到被压缩橡胶O形圈承受压力时,接触应力曲线具有抛物线特性。关文锦等[3]采用ABAQUS有限元分析软件对O形圈Von Mises应力、接触应力、接触长度等进行模拟,并使用理论接触公式对有限元分析结果进行验证,证明了有限元结果的可靠性。以上都是一些静态接触密封,原理简单,但适用范围不是很广,有利有弊。随着近些年密封领域的发展,密封的机理也是越来越多,密封技术也越来越成熟。为了满足高速转动的机构实现密封,出现了很多形式的机械密封[4],开发了纳米材料机械密封和应用纳米冲洗液进行密封,成功地利用密封机理设计制造了机械密封产品,其原理也是越来越多,比如利用涡流原理的槽型密封、干气密封、非接触式的机械密封[5]、迷宫密封等。研究采用O形圈密封装置,利用Ansys Workbench对整个机构进行多柔体动力学仿真,主要模拟零件的应力应变和运动,最终得出密封压力。

1 理论基础

1.1 多体动力分析理论

多体系统动力学是研究多体系统运动规律的科学。多体系统动力学包括多刚体系统动力学和多柔体系统动力学。虽然经典力学方法原则上可用于建立任意系统的微分方程,但随着系统内分体数和自由度的增多,以及分体之间约束方式的复杂化,方程的推导过程变得极其繁琐。为适应现代计算技术的飞速发展,要求将传统的经典力学方法针对多体系统的特点加以发展和补充,从而形成多体系统动力学的新分支。为建立多体系统动力学的数学模型,已经发展了各种方法,其共同特点是将经典力学原理与现代计算技术结合。这些方法可归纳为两类,即相对坐标方法和绝对坐标方法[6-8]。

相对坐标系法以Roberson-Wittenburg方法为代表,是以系统的每个铰链的一对邻接刚体为单元,以一个刚体为参考物,另一个刚体相对该刚体的位置由铰链的广义坐标来描述,广义坐标通常为邻接刚体之间的相对转角或位移。这样开环系统的位置完全可由所有铰的拉格朗日坐标阵q所确定。其q动力学方程形式为拉格朗日坐标阵的二阶微分方程组,即

采用绝对坐标方法,即以系统中每一个物体为单元,建立固结在物体上的坐标系,刚体的位置相对于一个公共参考基进行定义,其位置坐标统一为刚体坐标系的笛卡尔坐标与坐标系的方位坐标,方位坐标选用欧拉角或欧拉参数,单个物体的位置坐标在二维系统中为3个,三维系统中为6个。由于有N个刚体组成系统,位置坐标阵q中坐标个数为3N或6N个,由于铰链的存在,这些位置坐标不独立。系统动力学模型一般形式可表示为

其中:φ为位置坐标q的约束方程;φq为约束方程的雅克比矩阵;λ为拉格朗日成子。以上即为欧拉—拉格朗日方程组,其方程个数多,但系数矩阵呈稀疏状,可以使用计算机自动建立统一的模型进行处理。

1.2 瞬态动力分析理论

瞬态动力学分析是用于确定结构承受任意随时间变化载荷的结构动力学响应的一种方法。可以用来确定结构在静力载荷、瞬变载荷和简谐载荷的任意组合作用下的随时间变化的位移、应力和应变。动力学有限元方程推导如下[9]:

平衡方程为

几何方程为

物理方程为

边界条件为

初始条件为

构造位移差值函数:

由于只对空间域进行离散,所以单元内位移u、v、w的差值分别表示为

形成系统的求解方程:

平衡方程(1)及力的边界条件式(4)的等效积分形式的伽辽金提法可表示如下:

将空间离散后的位移差值表达式带入式(8),并注意到结点位移变化δa的任意性,最终得到系统的求解方程为

其中:[M]为质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵为节点位移加速度向量为节点位移速度向量;{F(t)}为随时间变化的载荷向量。

2 密封装置瞬态动力分析

2.1 问题描述

密封装置在实现密封的过程中,压力缸产生压力载荷,推动三角架做旋转运动,由于三脚架旋转运动受到凹槽的约束,旋转的同时沿轴向移动,推动压盖下移,压盖挤压塑性垫圈完成密封,同时三角架和压盖之间有个弹簧链接,在运动的同时弹簧不断拉伸来控制运动的平稳,模型见图1。压盖轴向最大位移为4 mm,三脚架最大转角为26°,推杆行程为6 mm,壳体内径为83.5 mm,外径为90 mm,弹簧自由长度为66 mm,刚度系数为300 N/mm。

图1 装置模型Fig.1 Device model

密封装置的压盖采用铝合金,三脚架采用钛合金,密封圈采用铟,其他部位皆为铝合金。

采用Ansys Workbench软件对模型进行多体动力分析,模拟整体运动情况,得到位移、应力和应变等结果,以验证零件强度和密封效果。

2.2 分析结果

压力缸产生的冲击力为2 000 N,计算时选择阶跃加载方式,对整体结构进行刚体动力分析,得到旋转部件的角速度、角加速度以及移动部件的速度、加速度。发现在0.25 s时,弹簧已经压缩至最大,所以分析结束时间为0.25 s,载荷步数为1,子步数最初为50,最大为100。求解器为direct,收敛算法为Full法[10,11]。

在刚体动力分析的基础上,对整体结构进行柔体瞬态动力分析,得到关键部件的应力、应变分布。最大应力变化曲线见图2,由图2可知在0.155 2 s时应力达到最大值,并且由图3所示的应变分布云图可知最大值发生在支架凸起处。图4表示压盖轴向位移曲线。因为压盖直接和密封圈接触,其轴向位移影响着密封圈产生塑性变形的大小,由图4可知轴向位移随着时间逐渐增大,最终收敛于一个最大值,其最大值为1.041 mm。图5为弹簧拉力的变化曲线。弹簧控制着支架旋转运动的速度,保证整个装置运动平稳,在密封装置启动时,由于各部件惯性力存在,运动速度逐渐增大,弹簧拉力变化不是很快,在经过加速之后,弹簧开始被拉伸,因为弹簧力的逐渐增大,抵消一部分惯性力,使速度没有大的突变,最终在0.23 s时由于阻力的增大收敛于1 534.8 N。图6为密封压力变化曲线。随着装置的运动逐渐到达极限状态,在0.23 s时密封压力达到最大值8 153.1 N,完成密封,其值是验证密封效果的关键数据。

图2 最大应力变化曲线Fig.2 Curve of the maximum variation of stresses

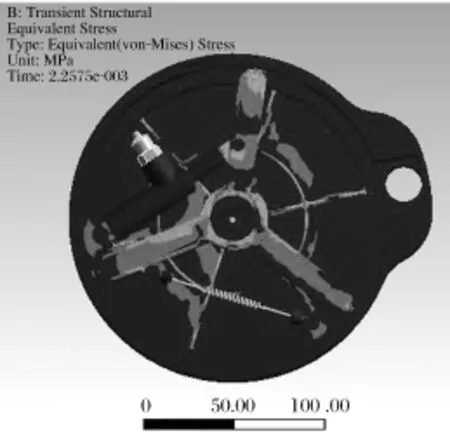
图3 应力分布云图Fig.3 Distribution of stress

图4 压盖轴向位移曲线Fig.4 Axial displacement curve of gland

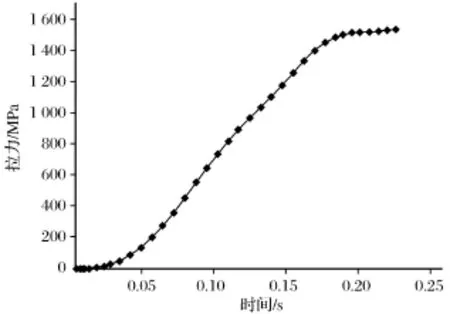
图5 弹簧拉力变化曲线Fig.5 Spring tension variation curve

图6 密封压力变化曲线Fig.6 Variation curve of sealing pressure

3 结论

(1)通过瞬态动力学分析可知整个结构只有压盖和支架受力比较明显,压盖应力比较小且均匀。相反支架受力不均匀,在支架与外壳体接触处容易出现应力集中。

(2)整个密封过程运动比较平稳,速度和位移没有比较大的突变,符合实际要求。

(3)当机构运动到极限状态时,密封压力达到8 153.1 N,此时密封盖产生的应力为σ＝F/A＝

4.535 MPa,使金属铟产生屈服,达到预期密封效果。

[1] 胡殿印,王荣桥,任全彬,等.橡胶O形圈密封结构的有限元分析[J].北京航空航天大学,2005,31(2):256-260.

[2] 陈志,高钰,董蓉,等.机械密封橡胶O形圈密封性能的有限元分析[J].四川大学学报:工程科学版,2011,43(5):235-239.

[3] 关文锦,杜群贵,刘丕群.橡胶O形圈密封性能的有限元分析[J].润滑与密封,2012,37(6):61-64.

[4] 孙见君,魏龙,顾伯勤.机械密封的发展历程与研究动向[J].润滑与密封,2004,29(4):128-131.

[5] 王玉明,刘伟,刘莹.非接触式的机械密封基础研究现状与展望[J].液压气动与密封,2011,31(2):29-32.

[6] 王国平.多体系统动力学数值解法[J].计算机仿真,2006,23 (12):86-89.

[7] 洪嘉振.多体系统动力学理论、计算方法和应用[M].上海:上海交通大学出版社,1992.

[8]Krzysztof Zboinski.Modelling Dynamics of Certain Class of Discrete Multi-body Systems Based on Direct Method of the Dynamics of Relative Motion[J].Meccanica,2012(47):1 527-1 551.

[9] 王勖成.有限单元法[M].北京:清华大学出版社,2003.

[10] 浦广益.Ansys Workbench基础教程与实例详解[M].北京:中国水利水电出版社,2013.

[11] 王君,朱延飞,王社敏.基于ANSYS的箍紧装置有限元分析[J].甘肃科学学报,2009,21(4):97-99.

Sealing Device Multi-body Dynamic Analysis

Ma Yongbin,Zhang Wenqiang,Zhao Guowen
(School of Sciences,Lanzhou University of Technology,Lanzhou730050,China)

Aiming at sealing packaging system,this text uses finite element method to analyze multi-body dynamics and simulate sealing effect so as to get displacement of rotating parts,tension variation situation of spring and variation curve of sealing pressure.Then,the structure is analyzed for its transient state of soft body and stress and strain of main parts in the whole sealing process is achieved so that strength and sealing effect of part can be verified.

Sealing system;Dynamics analysis of transient state;Rigid-soften coupling;Many-body dynamics

TB42

:A

:1004-0366(2016)05-0019-04

2015-12-07;

:2016-01-28.

甘肃省自然科学基金项目(148RJZA007).

马永斌(1974-),男,甘肃靖远人,硕士,副教授,研究方向为结构优化、多场耦合分析.E-mail:Myb_126＠163.com.

Ma Yongbin,Zhang Wenqiang,Zhao Guowen.Sealing Device Multi-body Dynamic Analysis[J].Journal of Gansu Sciences,2016,28(5):19-22.[马永斌,张文强,赵国文.密封装置多体动力分析[J].甘肃科学学报, 2016,28(5):19-22.]

10.16468/j.cnkii.ssn1004-0366.2016.05.005.