一个类Lorenz系统的混沌特性分析

尹社会,汤志浩

(河南工业职业技术学院,河南南阳 473000)

一个类Lorenz系统的混沌特性分析

尹社会,汤志浩

(河南工业职业技术学院,河南南阳 473000)

通过理论和数值模拟分析了一个多维类Lorenz超混沌系统的非线性特性和部分动力学行为。主要从对称性、耗散性、空间相图、Poincare映射图、分岔图等几方面展示了系统的动力学特性,并探讨了混沌吸引子的形成机制。结果表明,系统的全局指数吸引集及其计算机数值计算不仅验证了结论的正确性,而且为混沌控制和混沌同步提供了理论基础。

类Lorenz混沌系统;分岔;耗散性;全局指数吸引集

混沌这一名词的出现,标志着一个新学科的诞生,也意味着这一学科将越来越重要。1963年美国科学院院士Lorenz在研究大气对流时,首次给出了一个简单的三维自治系统,即著名的Lorenz系统[1],所采用的办法就是对Navier-Stokes方程和热传导方程进行Fourier级数展开并截取前三项。这已经成为现在非线性科学研究混沌系统的一个范式,后来又有其他学者进行有限项截断,得到不同模数的非线性微分方程组[2-9]。混沌吸引子是相空间中的一个点集,随着运动时间的增加,所有轨线都趋向于它。这些混沌系统的全局吸引子的存在性和部分动力学行为已经被许多研究者所认识和研究。除了Lorenz系统族之外,也存在其他混沌系统或超混沌系统,这些新混沌系统或超混沌系统的提出和研究为混沌系统甚至混沌理论的应用提供了一定的理论基础和参考价值[10-12]。我们进一步考虑文献[13]中提出的混沌系统,通过数值仿真给出了系统的相图、Lyapunov指数谱图、分岔图等研究系统的动力学特性,并借助数值仿真进一步分析了混沌吸引子的形成机制。

1 数学模型及其全局动力学特性

王贺元等[12]研究的一个七模Lorenz超混沌系统的方程为

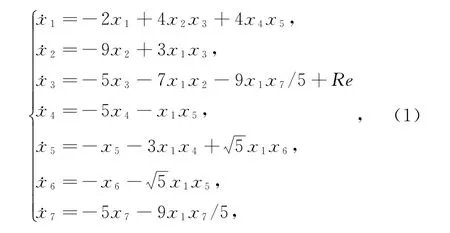
系统(1)在坐标变换P∶(x1,x2,x3,x4,x5,x6,x7)➝(x1,x2,x3,－x4,－x5,－x6,x7)下保持不变,说明系统具有该变化下的对称性。

根据刘维尔定理,系统(1)的平均散度∇V＝说明系统(1)是耗散的。当Re＝100时,初值取x1＝1,x2＝1,x3＝1,x4＝1,x5＝1,x6＝1,x7＝1,系统(1)的轨线的吸引子相图如图1所示。由图1(a)可以看出,在运行时间减半的情况下,吸引子只是在一个区域运动,并没有过渡到另一部分;从动态过程显示,反之亦然。由图1 (b)可以看出,吸引子的形状与Lorenz蝴蝶状明显不同,分别在两个不同的区域反复折叠,中间的连接过渡并不太频繁。

当Re＝120时,在初值不变的情况下,系统(1)的吸引子表现出更复杂的运动行为,先是绕一个吸引点旋转几圈,然后跳到另一个吸引点再绕几圈,如此反复,没有规律,形成典型的双叶片状吸引子(在图示相空间投影下),如图1(c)所示。

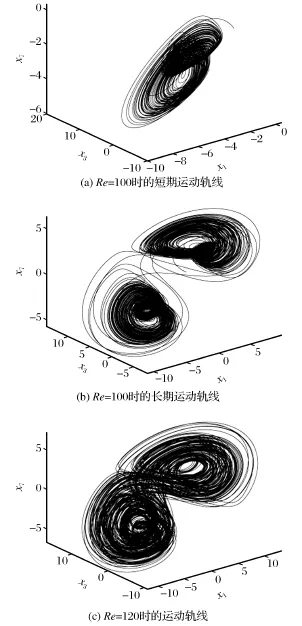
图1 系统(1)的轨线相图Fig.1 Trajectory phase diagram of system(1)

2 混沌吸引子的形成机制

由图1混沌吸引子相图随着参数Re的变化而发生的变化可以看出,参数Re对于混沌吸引子的形成具有重要的影响。下面进一步分析混沌吸引子的形成问题。

随着参数Re的变化,系统表现出稳定到平衡点、极限环和混沌吸引子等不同的非线性行为,即出现Hopf分岔和混沌现象。图2为参数在Re∈[70,130]的Lyapunov指数谱图(为了突出比较,图中只给出了最大的两个Lyapunov指数Le1、Le2)。图2中可以显示极限环、混沌和超混沌三种状态,进一步通过分岔图也可以验证这一特征,并且二者结论非常一致,如图3所示。在状态变量的初值不同时由分岔图可以进一步分析系统的混沌特性,从区间放大图(这里取对称的两组初值)可以看出,与图1所示相图在参数Re＝100附近的动力学行为是一致的。

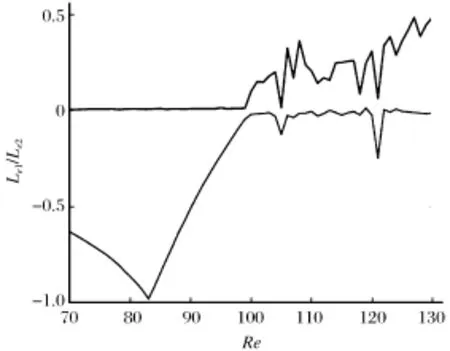
图2 系统(1)的Lyapunov指数谱图Fig.2 Lyapunov index spectrogram of system(1)

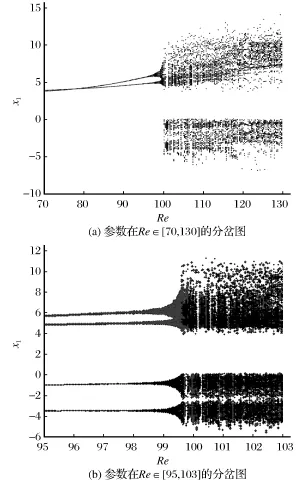
图3 系统(1)的分岔图Fig.3 Bifurcation diagram of system(1)

当参数Re＝80时,初值分别为x1＝－1,x2＝－1,x3＝－1,x4＝1,x5＝1,x6＝1,x7＝－1和x1＝1,x2＝1,x3＝1,x4＝1,x5＝1,x6＝1,x7＝1下的吸引子如图4所示,对称的运动分别在两个吸引域内。由以上分析可以看出,参数Re对于系统(1)形成混沌吸引子具有重要的调节作用。从系统(1)的平衡点的分布情况来看,当参数Re达到一个值后,3个平衡点均变得不稳定,这为上述混沌吸引子的形成找到了理论上的吸引域中心,即吸引子总是围绕吸引域的中心做运动,具体运动行为取决于平衡点的特征值分布。

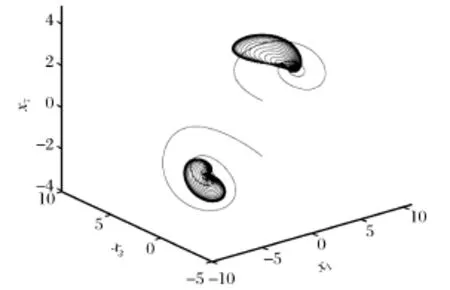
图4 系统(1)在对称初值下的极限环相图Fig.4 Limit cycle phase diagram of system(1) under symmetry initial value

3 全局指数吸引集及其数值模拟

下面给出系统的全局指数吸引集的结论。

定理1令则当V(X(t))≤(Re/5)2,(t≥t0)时,系统(1)有如下的指数估计式:

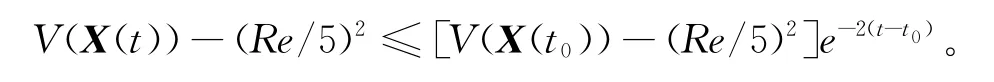
特别地,集合

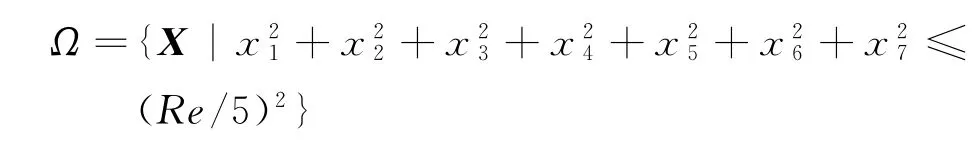
是系统(1)的全局指数吸引集。

当参数Re＝120时,系统(1)的最终界估计的计算机仿真如图5所示。由图5可以看出,系统的状态变量的数值模拟和理论估计结果吻合比较好。

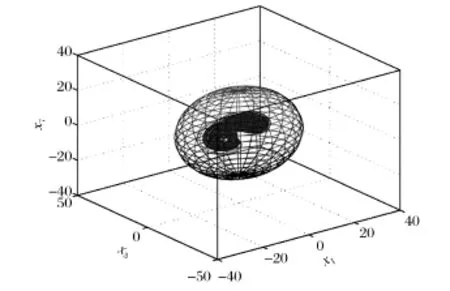
图5 系统(1)的混沌吸引子的最终界Fig.5 The ultimate bound of system(1)

为了清楚理论估计和仿真模拟计算结果的比较,具体情况如表1所列。由表1可以看出,不仅仿真模拟计算结果全部落入全局指数吸引集内,而且各个状态变量在长时间的运动行为中也表现出很强的对称性,这也符合混沌系统的全局有序性和局部混乱性的特点。

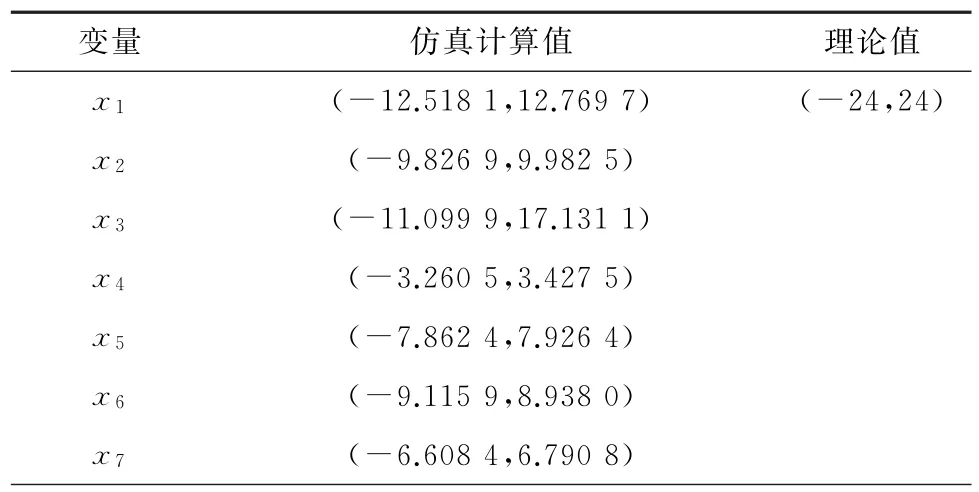
表1 系统(1)的界估计值Table 1 The bounds for system(1)

4 结论

基于系统(1)的参数敏感性,讨论了其运动轨线的变化情况,详细阐述了随着参数变化系统的动力学行为变化及其混沌吸引子的形成机制。结合Lyapunov指数谱图和在对称初值下的分岔图,研究了参数Re变化时系统(1)的部分动力学行为和全局指数吸引集,并且通过计算机数值计算验证了系统(1)的全局指数吸引集的正确性。这些结论不仅为系统(1)的混沌同步和混沌控制提供理论依据,也为电子电路的实现及其在通信工程等方面的应用提供了理论基础。

[1] Lorenz E N.Deterministic Non-periods Flows[J].J.Atoms.Sci.1963,20(2):130-141.

[2] Valter Franceschini,Claudio Tebaldi.A Seven-modes Truncation of the Plane Incompressible Navier-Stokes Equations[J].Journal of Statistical Physics,1981,25(3):397-417.

[3]Carlo Boldrighini,Valter Franceschini.A Five-dimensional Truncation of the Plane Incompressible Navier-Stokes Equations[J].Communications in Mathematical Physics,1979,64 (2):159-170.

[4] Franceschini V,Zanasi R.Three-dimensional Navier-Stokes E-quations Truncated on a Torus[J].Nonlinearity,1992,4(3): 189-209.

[5] Franceschini V,Nglese G,Tebaldi C.A Five-modes Truncation of the Navier-Stokes Equations on a Three-dimensional Torus[J].Communications in Mathematical Physics,1988,3 (1):19-37.

[6] 王贺元,鞠春贤.四模Lorenz系统的动力学行为及其数值模拟[J].高校计算数学学报,2010,32(2):99-105.

[7] 王贺元,姜悦岭.平面不可压缩的Navier-Stokes方程的新五模类Lorenz方程组的混沌行为[J].数学杂志,2010,30(2): 269-272.

[8] 王贺元.Navier-Stokes方程五模类Lorenz方程组的动力学行为及数值仿真[J].应用数学与计算数学学报,2010,24(2): 13-22.

[9] 尹社会,张勇,张付臣,等.基于Lorenz系统的强迫Lorenz混沌系统的动力学研究[J].东北师大学报:自然科学版,2014, 46(1):42-47.

[10] 尹社会,李德雪,张勇.新三维非线性系统的全局动力学研究[J].甘肃科学学报,2015,27(4):87-90.

[11] 陈红,周攀.一个四维系统的混沌动力学分析[J].甘肃科学学报,2013,25(1):13-16.

[12] 尹社会,张勇,皮小力.自治混沌系统的动力学行为及计算机仿真[J].广西物理,2015,36(1):32-37.

[13] Wang Heyuan,Cui Yan,Huang Min.A New Seven-modes Truncation of the Plane Incompressible Navier-Stokes Equations[J].Chinese Quarterly Journal of Mathematics,2012,27 (1):11-17.

Chaotic Characteristics Analysis of a Lorenz-like System

Yin Shehui,Tang Zhihao
(Henan Polytechnic Institute,Nanyang473000,China)

By theory and numerical simulation,analyze nonlinear characteristic and part dynamics behavior of multi-dimensions Lorens super chaotic system.From symmetry,dissipativeness,space phase diagram, Poincare map and bifurcation diagram,this text presents dynamic characteristic of system and discusses formation mechanism problem of chaos attractor.The achieved overall index attracting collection of system and numerical calculation of computer not only verifies conclusion,but also offer theory basis for chaos control and chaos synchronization.

Lorenz chaos system;Fork;Dissipativeness;Overall index attracting collection

O357.1;O241.82

:A

:1004-0366(2016)05-0034-04

2015-09-10;

:2015-10-14.

河南省基础与前沿技术计划项目(142300410416).

尹社会(1979-),男,河南沈丘人,讲师,研究方向为非线性动力学和混沌控制.E-mail:hnzkny＠126.com.

Yin Shehui,Tang Zhihao.Chaotic Characteristics Analysis of a Lorenz-like System[J].Journal of Gansu Sciences,2016,28(5):34-37.[尹社会,汤志浩.一个类Lorenz系统的混沌特性分析[J].甘肃科学学报,2016,28 (5):34-37.]

10.16468/j.cnkii.ssn1004-0366.2016.05.009.