拨开迷雾 找准方向——从高三复习课《圆锥曲线》一道例题的化简方法谈起

张跃红

（南京师范大学附属中学 210003）

在高三复习中，圆锥曲线部分的解答题是让教师和学生都比较头疼的.因为在测试中，它并不属于真正的难题，本应该通过复习能取得不错的成绩.但事实上，教师劳心费力，收效却甚微.学生一旦遇到综合性题目，往往头绪万千，深陷其中，而不能自拔，最后无功而返.那么，如何才能让学生尽快理清思路，从“迷雾”中走出？本文结合高三复习课中一道例题的化简方法，谈一些想法与同行交流.

1 一个例题

如图1，在平面直角坐标系xOy中，已知椭圆的离心率为，两个顶点分别为A1（-2，0），A2（2，0）. 过点D（1，0）的直线l交椭圆于M，N两点，直线A1M与A2N的交点为G.

图1

（1）求椭圆的标准方程；

（2）求证：点G恒在一条定直线上.

本题的第（2）问是比较常见的问题，解决问题的关键在于如何处理直线与椭圆的交点.虽然圆锥曲线的解答题会涉及到各类型的问题，比如求值，最值与范围，定点、定值等等，但归根结底都会与直线和圆锥曲线的交点有关.而事实上，学生处理不好圆锥曲线问题往往就是因为不清楚是“设点”，“设直线”，还是“求点”？以至于“东想西想”列出来一堆式子，而面对它们又不知道要做些什么，理不清思路，最后只好作罢.

那么，面对这样的问题，到底应该如何思考？

2 多种解法

2.1 直接求

方法1设直线A1M的方程为y=k1（x+2），直线A2N的方程为y=k2（x-2）.

消去y得

解得点M的坐标为

同理，可解得点N的坐标为

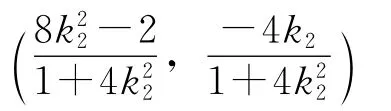
由M，D，N三点共线，

化简得（k2-3k1）（4k1k2+1）=0.

由题设可知k1与k2同号，

所以k2=3k1.

解得交点G的坐标为

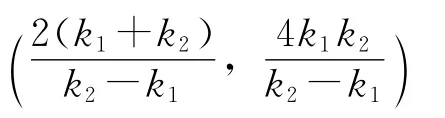
将k2=3k1代入点G的横坐标，得

所以，点G恒在定直线x=4上.

从方法1的解答过程中知道，在求M，N两点的坐标时，联立方程组是算了两次的.能只算一次吗？

2.2 以一代二

方法2设直线A1M的方程为y=k1（x+2），

直线A1N的方程为y=k3（x+2），

直线A2N的方程为y=k2（x-2）.

消去y得

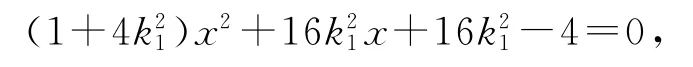
解得点M的坐标为

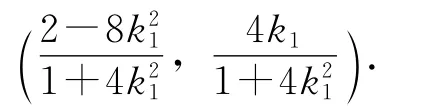
将k1替换成k3，可得点N的坐标为

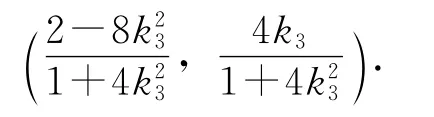
化简可得点N的坐标为

下面解法同方法1.

还有其他解法吗？

2.3 设而不求

方法3由已知条件，可猜出点G恒在直线x=4上.

证明如下：显然，直线MN的斜率为0时不合题意.

设直线MN的方程为x=my+1，

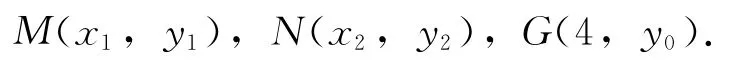
由点A1，M，G三点共线，有

再由点A2，N，G三点共线，

将x1=m y1+1，x2=m y2+1代入①式，

化简得2my1y2-3（y1+y2）=0. ②

消去x得（m2+4）y2+2m y-3=0，

从而有

将其代入②式，有

所以，当m为任意实数时，

点G恒在定直线x=4上.

方法3是先将直线MN的位置特殊化（比如垂直于x轴），猜出结论，再进行证明.当然，也可以直接证明.

方法4设M（x1，y1），N（x2，y2），

直线A1M的方程为，

直线A2N的方程为

解得交点G的横坐标

由M，D，N三点共线，

化简可得y1x2-y2x1=y1-y2，

将其代入点G的横坐标，可得

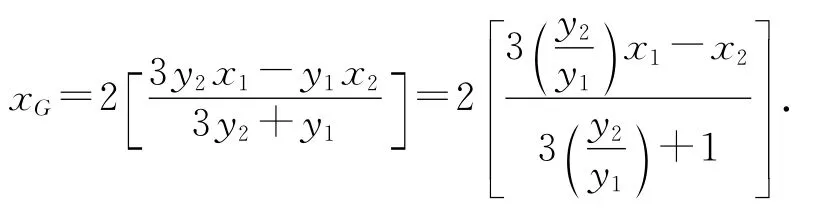
代入点G的横坐标，

由点M，N在椭圆上，

化简得

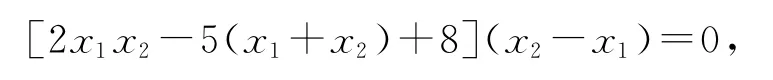
即x1=x2或2x1x2-5（x1+x2）+8=0.

当x1=x2时，由M，D，N三点共线，

可知x1=x2=1，与x1≠1且x2≠1矛盾，

所以2x1x2-5（x1+x2）+8=0.

当x1=x2=1时，可知

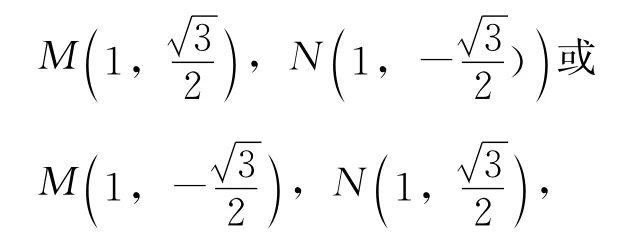
满足xG=4.

综上所述，点G恒在定直线x=4上.

3 比较分析

从本题的四种解法中，可以看出：方法1和2，与方法3和4在处理直线与椭圆的交点M，N坐标时，采用的方式是完全不同的.前两种采用的方法是“直接求”，而后两种是“设而不求”.

那么，何为“直接求”与“设而不求”？它们之间有什么区别、联系？应在何种情况下使用？

所谓“直接求”是指，在处理圆锥曲线与直线的交点坐标时，联立直线与圆锥曲线的方程组，通过解方程直接求出它们交点；而“设而不求”，则只是将它们用坐标的形式表示出来（即M（x1，y1），N（x2，y2）），然后再根据已知条件，找到它们坐标之间的等量关系，进而运算、化简.

方法1和2虽然在运算上有些繁，但在思维与化简能力上的要求并不高.究其原因，是因为直线A1M（或直线A2N）与椭圆的两个交点，都有一个点A1（或A2）的坐标是已知的，如果需要求另一个交点M（或N）的坐标，即转化为解方程问题.接下来，解题线索会很快理清，只需寻找k1和k2的关系（M，D，N三点共线），然后将其代入点G的坐标，问题迎刃而解.所以，“直接求”可作为处理“直线与圆锥曲线相交时，已有一个交点坐标确定”的情况下这类问题的首选，把它作为解题的突破口，然后再根据其他条件化解题目.

可以发现，方法2比方法1的化简要简单一些，原因是少求一次交点坐标.方法1用了完全不相关的两条线（A1M和A2N）与椭圆方程联立求交点.而方法2却用了过同一点A1的两条线（A1M和A1N）与椭圆联立.在求出交点M的坐标后，点N的坐标则无需再求.因为直线A1M和A1N与椭圆联立之后得到的方程，只有k1与k3是不同的，其余完全相同，所以只需将点M坐标当中的k1替换成k3，即可得到点N的坐标.称其“以一代二”，即“用一次运算代替二次运算”，从而实现了简化运算的目的.

除此之外，“以一代二”还有另外一个用途，即“用一个方程代替二个方程”.比如，在化简运算中遇到2x21+3x1-4=0且2x22+3x2-4=0时，有时并不需要将x1和x2的值分别求出，可以用一个一元二次方程2x2+3x-4=0代替它们两个方程，而x1和x2则是此一元二次方程的两个根，可用韦达定理和x1x2=-2进行整体代换，简化运算.

“设而不求”中的“设”是非常容易的.如何找到所设若干未知量的等量关系，以及在列出的多个关系式中理清所求目标与这些未知量之间的联系，才是重中之重！

虽然方法3和4都采用了“设而不求”，但化简过程明显不同.

方法3，当猜出点G恒在定直线x=4上的结论后，需要证明的关键等量关系是.而此等式存在四个未知量，消元势在必行.等式①是由点M，N分别在直线A1G和A2G上的“身份”得到的，挖掘点M，N的其他“身份”得到等式进而再消元便是关键.易知，点M，N还有两重“身份”：在椭圆上及直线MN过点D.由于等式①均为一次形式，若用在椭圆上的“身份”消元显然不合适，所以利用它们的另一重“身份”设出直线MN的方程x=m y+1消去x，得到方程2m y1y2-3（y1+y2）=0，再借助韦达定理进行整体代换.

设直线MN的方程时，需要考虑设成哪种形式，是x=my+1？还是y=k（x-1）？如本题，直线MN的斜率不为0，且斜率存在与否都有可能，最好设成x=my+1，避免斜率的讨论.一旦设成此种形式，在与椭圆方程联立时，最好消去x，得到关于y的一元二次方程，这样运算简单.若直线MN的斜率一定存在时，可设成y=k（x-1）的形式，再与椭圆方程联立可消去y，会更方便运算.

方法4，先要分析交点的多重“身份”（比如M，N两点在椭圆上，又满足M，D，N三点共线，还满足直线A1M与A2N的交点为G），根据它们的多重“身份”列出不同的等量关系.比如，点M，N在椭圆上，有；M，D，N三点共线，有；直线A1M与直线A2N的交点为G，可得点G的横坐标为xG=.

接下来，至关重要的是如何处理这些方程！

（1）判断未知量的个数与方程的个数是否匹配.如果匹配（即未知量与方程个数相等），未知量均可求.之后，对若干方程进行四则运算，问题便迎刃而解；

（2）如果不匹配，比如方法4，5个未知量x1，y1，x2，y2，xG，却只列出4个方程（①、②、③、④），未知量的值是不可能全部求出的，化简的“终极目标”必是将某两个未知量间的关系代入所求方程④.这些未知量留谁？去谁？看结构！所求目标④过于复杂，但观察到未知量y1x2，y2x1同时出现，故可先利用③的整式形式y1x2-y2x1=y1-y2进一步化简，得到xG=.通过观察，可以发现此式为分式结构，且分子、分母均含有y的一次形式.若同时除以y1，出现，而又有，若将其代入只会出现两个未知量x1和x2间的关系，这与我们的预期不谋而合.倘若再寻找到x1和x2间的关系，然后再代入所求目标，问题便可解决.事实上，，很快找到了x1和x2间的关系.

从前面的比较分析中，可以看出“设而不求”对方程“掌控”能力的要求是比较高的.其关键在于对所“设”的若干未知量的处理，是能求出未知量的值？还是只能利用关系进行整体代换？要做到心中有数.至于用哪些未知量的关系进行代换，一定要根据结构来决定.

一般情况下，“设而不求”是比较适合于直线与圆锥曲线的交点均未知的情况.因为“设而不求”的化简要求比较高，如果已知一交点坐标，不如“直接求”这样比较“省心”.当两个交点的坐标都未知时，它的优越性才会显现.

4 思考线索

处理好直线与圆锥曲线的交点是解决圆锥曲线问题的核心，决定了整个问题的“发展”方向.只有交点问题处理清楚找对方向了，才会为后面的解答铺平道路.

鉴于此，并基于以上不同解法的比较分析，总结概括出处理直线与圆锥曲线交点问题的思考线索：

（1）合理使用“直接求”与“设而不求”两种方法.

若已知直线与圆锥曲线的一个交点坐标，对待另一交点的坐标，采用“直接求”的方法相对容易找到解决问题的突破口；若两交点均未知，可使用“设而不求”.

（2）使用“直接求”时，一方面，需考虑将直线方程设成哪种形式（比如y=kx+b或x=my+n）；另一方面，需考虑是否可以使用“以一代二”的化简方法.通常情况下，“以一代二”往往可以和“直接求”结合起来使用，达到事半功倍的效果.

（3）使用“设而不求”时，第一，需考虑交点有几重“身份”，根据不同的“身份”列出方程.第二，需考虑未知量与方程的个数是否匹配.若匹配，未知量均可求；若不匹配，只能求出其中某些未知量的关系.第三，需考虑化简若干方程的途径.通常情况下，化简途径有两种：借助韦达定理进行整体代换；或是根据方程的结构特点，选择易被消去的未知量，利用四则运算进行化简.

当然，上述思考线索并不是绝对的，还需要具体问题具体分析.但至少可以让我们在遇到圆锥曲线问题时，有一个明确的方向，在各种纷繁复杂的头绪中，尽快理清思路，少走弯路.