从直觉思维看“以图代证”的是与非

严亚强

（苏州大学数学科学学院 215006）

“直觉就是直观感觉，是没有经过思考和分析推理的观点，是意识的本能反应.数学最初的概念都是基于直觉.数学在一定程度上就是在问题解决中得到发展的，问题解决也离不开直觉.数学直觉思维是具有意识的人脑对数学对象（结构及其关系）的某种直接领悟和洞察.直觉思维可以从两种意义上去理解.一方面，直觉思维是在丰富的知识与经验的基础上，在短时间内直观把握事物的本质，瞬间作出判断的思维形式；另一方面，直觉思维是灵感思维，或称‘顿悟’思维，灵感思维是经过长期思维瞬时顿悟，是思维信息迅速转化和急剧重组，形成新的信息系统，从而使思维出现新的突破……直觉思维不但要依托扎实、全面的知识背景，而且要依靠教师敏锐的眼光去发现、去捕捉并长期不懈地培养，才能不断闪现奇异的光芒.”[1]以上论述摘自赵光礼《数学素养新思维》一书.直觉思维是我们提倡的“用数学的方式思考问题”的重要数学素养.在培养创新型人才的社会要求下，这种思维能力显得弥足珍贵.

“以图代证”，顾名思义是指在数学上用图示代替推理论证的证明方式，被公认为是“不严格”的证明方式.但即使是不严格，作者认为，也有可取和不可取之分.例如中小学里的圆面积公式都是以图代证进行处理的，高中数学中涉及零点定理时的函数“连续性”是以图代证处理的.由于极限概念“说来话长”，用以图代证的方式就显得很合理.但如果为了证明一类问题的正确性，而用一个特殊图形来说明，例如在证明“在定义区间上导数大于零的函数必是单调递增函数”时画一条特殊曲线，或在证明“有两条竖直对称轴的函数必是周期函数”时用一个图像“如图所示”，就是不合理的.这里再给一个难以“以图代证”的例子.

例1已知点A为直线l：x+2y-4=0上任意一点，点C（2，4），以AC为直角边作直角三角形ABC，其中AB=AC（A，B，C按顺时针排列），求的最小值.

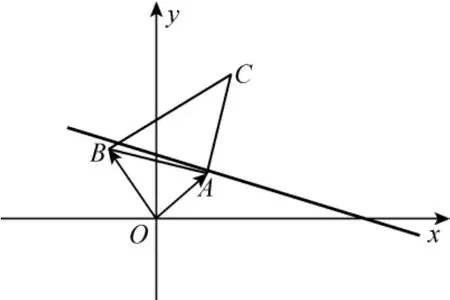
图1

解析我们知道函数的最大最小值必在区间的端点或区间内的某个特殊位置取得，若令点A向直线l的上方或下方运动到足够“远”处，则夹角是锐角是个很大的数，所以的最小值必在离原点“不太远”的某个特殊点取得，如果贸然猜侧这个点是O C与直线l的交点，就会出错.这时借助严格推理就不可避免.事实上，让取得最小值的A点坐标是.正确的解法是：

设A点坐标为（x，y），则（2-x，4-y），因是向量绕点A逆时针旋转θ=90°所得，所以，从而），.上式的最小值是以C（2，-1）为圆心的一簇圆的半径的平方减5的最小值，当然在圆与直线l相切时取得这个最小值，C（2，-1）到直线l的距离为，所以即为所求.

下面一例的特点恰恰相反，它需要依靠直觉而排除严格证法.

例2已知椭圆与圆C2：x2+y2=b2，若在椭圆C1上存在点P，使得由点P所作的与圆C2的两条切线互相垂直，求椭圆C1的离心率的取值范围.

图2

解析因为点P离圆心“越近”，两切线的张角就越大，当点P运动到接近上顶点N时，张角接近18 0°，当点P运动到右顶点M时，张角最小，所以“存在互相垂直的切线”当且仅当右顶点处的的张角2α≤90°，当且仅当，从而离心率

此题如果严格地推理，则复杂程度“不堪入目”，上面的过程可以说是典型的“以图代证”，不严格之处在于“当点P从上顶点N处沿椭圆C1运动到右顶点M时，为什么切线间的夹角是一个连续变化的过程？”如果把这个问题忽略，则上面的解析过程不失为十分精彩.

近年来，在参与中学评课时，或在审稿时，常常讨论到类似于下面例3的例题解法，因为辅之以图而遭到否定，原因是“以图代证”，实在替人冤屈.

例3求的值域.

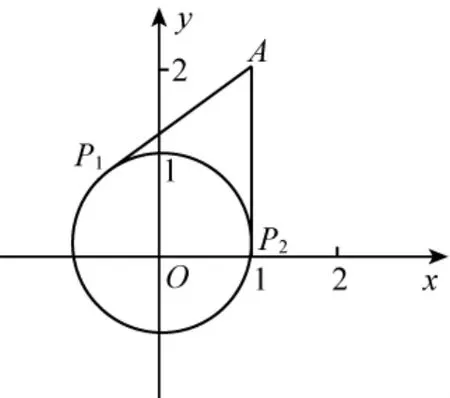
图3

解如图3所示，将y看作点A（1，2）到单位圆上C：x2+y2=1上动点P（a，b）的连线A P的斜率.过点A作圆C的两条切线：x=1和y-2=），所以斜率

这个解算不算正确？有的老师说：如果在填空题中只为求答案，则没有问题，但若在解答题中，则有补上求切线的过程.

求切线的过程很简单，是这样的：

若切线的斜率k存在，则设切线方程为y-2=k（x-1），由于原点O（0，0）到该直线的距离为1，即，立得，所以切线；另一切线斜率不存在，即.

但有的老师认为个过程仍要“扣分”，因为借助了图像；或者说，用斜率代表一个代数式总归是不可靠的.问题在于“借助图像”就一定属于“以图代证”了吗？“以图代证”的方法必不可取吗？这第一个问题属于数学方法论问题，第二个问题属于教学评价问题.作者认为本题的配图，并不造成解题中的逻辑关联，只是起到直观中的辅助作用，证明过程中的每一步都可以用“纯代数”的语言对应解释.但有了图示，可以帮助省去很多解题步骤，何乐而不为？

1982年，著名数学家、数学教育家徐利治从认识论的角度，通过深入考察数学思想发展史中的典型例子，以精确的数学语言提出了普遍数学中的“关系映射反演方法（Relationship Mapping Inversion）”，简称RMI方法，将人们自觉不自觉运用的化归思想上升到方法论的高度，可谓数学方法论的一大突破，其原理（如图4所示）大致如下：

图4

给定一个含有目标原像x的关系结构S，如果能找到一个可定映射φ，将S映入或映满S*，则可从S*通过一定的数学方法把目标映像x*=φ（x）确定出来，从而通过反演即逆映射φ-1把x=φ-1（x*）确定出来.

RMI方法是分析、处理数学问题的一种普遍方法，同时也属于一般科学方法论性质范畴的一种工作原则.它既可用来指导数学发现、叙述数学知识和展开数学理论，推动数学研究的深入进展，又可以处理具体数学问题，化难为易，化繁为简，使问题得到解决.[2]

在本题中，代数问题找到了几何上的一一对应，几何中解决了问题反演到了代数范围，从RMI方法的角度看毫无疑问是正确的.几何直观的合利利用是直觉思维的可贵表现，而直觉思维是创造力的主要因素，我们都呼唤着要培养学生创造性思维、发展数学核心素养，但到了高考大棒面前，变得胆战心惊、束手束脚.看来数学教育也期待着“思想解放”.

再看2016年的江苏高考数学第19题.

例4已知函数f（x）=ax+bx（a＞0，b＞0，a≠1，b≠1）.（1）设a=2，.①求方程f（x）=2的根，②若对于任意x∈R，不等式f（2x）≥m f（x）-6恒成立，求实数m的最大值；（2）若0＜a＜1，b＞1，函数g（x）=f（x）-2有且只有1个零点，求ab的值.

解析此题的第（2）问，一看便知.因，记，则g（x）在x0左侧递减、右侧递增，那么在有且仅有一个零点的条件下，这个零点必是使g（x）取了最小值的点x0，而显然x=0正是它唯一的零点，那么必有g′（0）=0，从而ab=1.

有些标准解答上强调要用反证法证明x0=0，也有的解答还强调，不可直接用，必须改取特殊值证明其值很大（大于零）.有关函数的零点是近年高考的热点，它的确是一类可以集数形结合、化归、函数、分类讨论四大数学思想方法于一身的良好题材，在江苏，2012年18题、2013年20题、2014年13和19题、2015年13题、2016年19题都考了函数零点，但是我们在评课研讨中发现，一些老师明明教会了学生一些简单的极限，却要警告学生“只能意味，不能写在解题过程里.”原因是怕引起“以图代证”的误会，特别是2016年的第19题的标准答案公布后，有的老师马上很负责任地强调，“今年的零点问题，凡不取特殊值（而写极限）的都会扣分”，原因是“今年的题目简单，会从严要求”.真是奇葩逻辑.

我们知道，教会学生取特殊的方向在于让学生明白函数的走向，函数在“远处”的性质就得依靠极限，老师们私下早已授予了这种方法，你说当x→+∞时谁能不了解极限为+∞？极限思想和无穷大思想都是数学中的重要数学思想？中学生若能够领会是一件好事，如果老师教会了学生又不允许学生写出来，属不属于对数学态度的一种扼杀？算不算对学生心智的一种摧残？是不是很残忍？如果我们的学生知道用来确定必有一个根，试问错在哪儿？他（她）都知道是趋于正（负）无穷了，还用得着再找两个特殊值吗？你若要严格按课本上的定理条件推理，那么你教学生如何证明这些函数的“连续性”的？要知道连续性的证明一向都是“以图代证”的.

对“以图代证”的现象不能过于严苛，它隐含着直觉思维的火花，在教改进行时的今天，不应继续回避对“以图代证”作出评价，而应该发展教学评价机制，让学生的直觉思维获得张扬.事实上，一味强调严格证明，也是对数学思想的片面理解.弗赖登塔尔提出的“严谨性原则”正是强调严谨的相对性、层次性、时代性，只有这样，才能通过“数学现实”原则，达到“数学化”和“再创造”的数学教育水准.