由勾股容方想到的

罗 伟 彭翕成 谭世鑫

（1.江苏省徐州市第二十四中学 221000；2.华中师范大学国家数字化学习工程技术研究中心 430079；3.北京大学城市与环境学院 100871）

勾股容方源于《九章算术》第九卷《勾股》章第十五题；“今有勾五步，股十二步，问勾中容方几何？答曰三步十七分步之九.术曰：并勾股为法，勾股相乘为实，实如法而一，得方一步.”

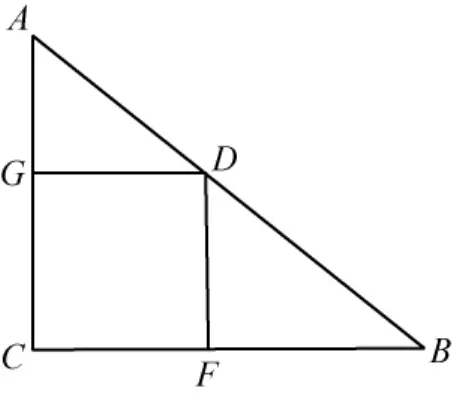
图1

如图1，直角三角形ABC中内接正方形DGCF.直角三角形勾AC=5，股BC=12，答案：以勾5步、股12步之和为分母（并勾股为法）；以勾5步股、12步之积为分子（勾股相乘为实）得勾中容方边长.勾股容方意思就是由三角形勾、股长度可以求出如图内接正方形的边长.

勾股容方的一般表示方法

例1在图1中，若AC=c，BC=d，设正方形DGCF的边长是x，则.

解法1拼图法

将题目中的图形等积变形如图2，

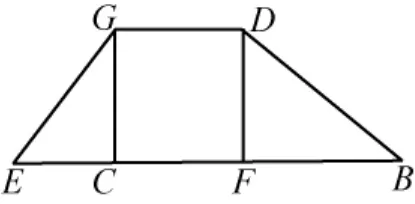
图2

原来三角形的面积等于重新组合后梯形的面积，

解法2相似三角形

注边长求出来，面积也可求，其余各三角形边长、面积也迎刃而解.

勾股容方变式一（已知两个小直角三角形两条直角边（勾、股分别减去正方形边长所得的线段）的长，也能求出正方形的边长.）

例2在图3中，若AG=e，BF=f，求正方形的边长.

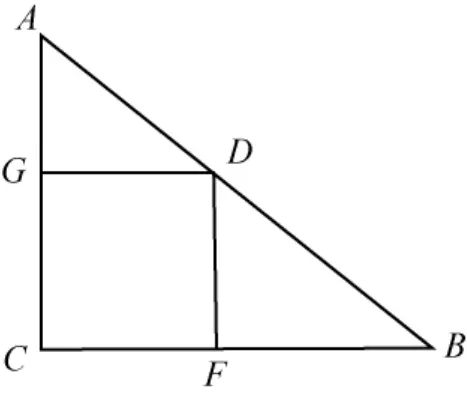
图3

解法1拼图法

用两个相同的直角三角形能拼成矩形，如图4，

通过观察可知S正方形DGCF=S矩形EDHI=ef，

所以正方形DGCF的边长是.

图4

解法2相似三角形

设正方形的边长是x，

勾股容方变式二（已知两个小直角三角形斜边的长，也能求出正方形的边长.）

例3如图1，直角三角形ABC是由两个小三角形和一个正方形拼成的.已知AD=b，DB=a，求正方形DGCF的边长.

设正方形DGCF边长为x，那么根据三角形相似，图中各边都能用a、b及x的代数式表示出来，即，，根据勾股定理有AC2+BC2=AB2，代入得（a+b）2解得

思考：勾股容方中，正方形是面积最大的正方形吗？

例4在图1中，所示正方形与边长位于斜边上的内接正方形相比，谁的面积更大？请说明理由？

图5

解析如图5，两个全等的直角三角形能拼成一个矩形，在直角三角形ABK中，正方形的一边落在AB上，另两个顶点在AK和BK上，设AD=b，DB=a，GD=x，EH=y，

由例3中的证明过程可知

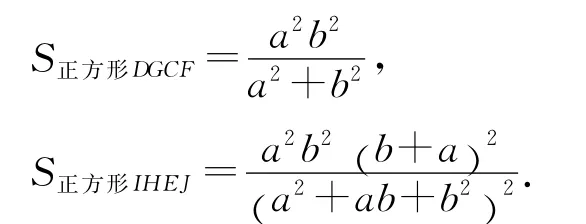
即证

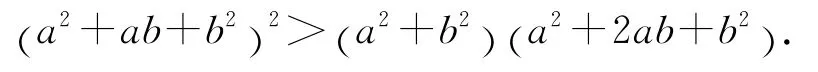
（m+n）2＞4m n即m2+n2＞2mn显然成立.得证.

注对于直角三角形内接最大正方形问题，教辅书上提供了一些方法，这种方法是一种新方法，在证明的过程中恰好利用例3中的结论，另外m2+n2＞2mn这一不等式对成绩好的学生可以向他们介绍，虽然在高中还要深入地学习，这样能扩大学生的知识面，提高学习兴趣.

证明了直角三角形内接最大正方形的问题之后，可应用到实际生活中.举例如下.

例5一顾客拿一个形状为直角三角形的布料去裁缝店，要求裁缝裁剪成面积最大的正方形布料，裁缝量得两直角边分别为40cm、60cm，一口说出这个方形的边长为24cm，顾客目瞪口呆，你知道是怎么计算出来的吗？

解析由例4的思路可以证明图1中的正方形是面积最大的正方形，再利用例1的结论，可得出边长为.

例6如图6，有一块菱形的地砖，要求切割成面积最大的正方形，工人师傅量了两条对角线的长度分别为40cm、60cm，一口说出这个方形的边长为24cm，你知道其中的缘由吗？

图6

解析四个全等的直角三角形可拼成一个菱形，与例5类似，可以证明图6中的正方形面积是最大的，菱形可分成四个全等的直角三角形，每个三角形中都有面积最大的正方形，边长为，所以拼成的大正方形的边长为12×2=24cm.

注 本题由直角三角形内接正方形问题过渡到菱形内接正方形问题，又巧妙借用了菱形对角线相互垂直的特点，解决了实际问题，本质没有区别，陶行知先生提出的生活即教育，显示了生活中处处用到数学.例5和例6则是孙维刚老师提出的多题归一，即寻求规律.

勾股容方变式三（已知两个小直角三角形斜边的长，求这两个小直角三角形面积的和.）

例7如图7，直角三角形ABC是由甲、乙两个小三角形和一个正方形拼成的.已知AD=b，DB=a，求S甲+S乙.（改编自2013年徐州市小学毕业考试题）

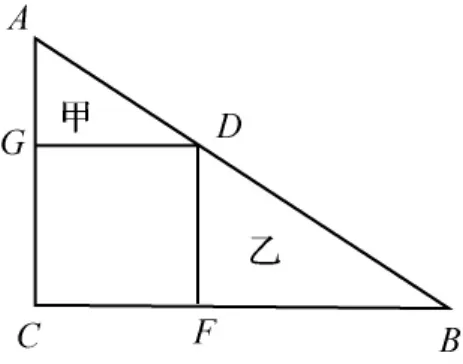
图7

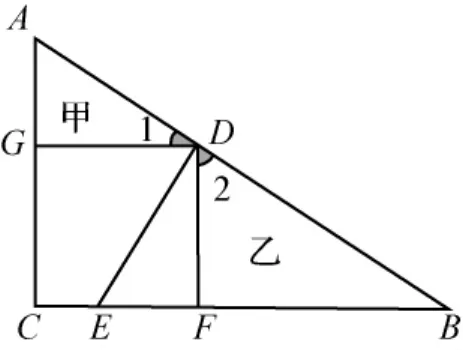
图8

解法1三角形全等

如图8，过点D作DE⊥AB，交BC于点E，因为∠1+∠GDE=90°，∠GDE+∠EDF=90°，所以∠1=∠EDF.又因为GD=FD，∠AGD=∠EFD，所以△AGD≌△EFD，可得DE=AD=b，所以.

注关键是辅助线的作法，有一些同学想不起来，对于证明三角形全等的过程学生比较熟练，此法是常规解法.

解法2三角函数

注这里由正切三角函数值直接求出正弦和余弦值，从而求解，思路简单清晰.

解法3相似三角形面积比等于相似比的平方

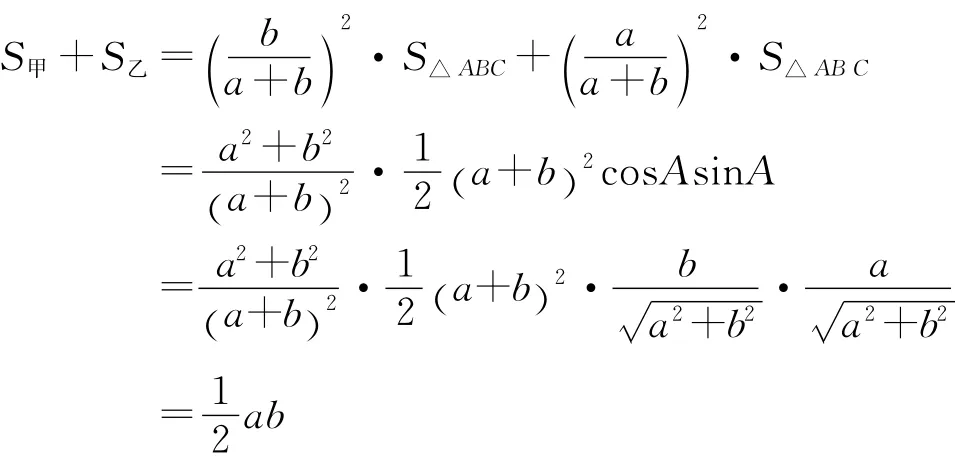
注此法也是由正切三角函数值直接求出正弦和余弦值，故过程省略.

解法4合比性质

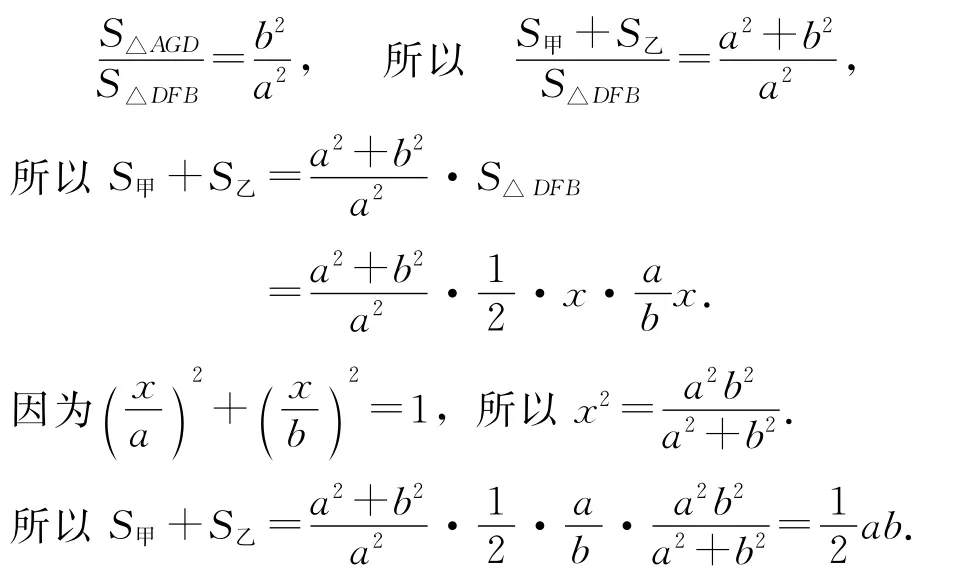
注这里主要用了比例的合比性质来求解，要先求出正方形的边长x的值，再带入求解.

解法5大三角形的面积减去正方形的面积

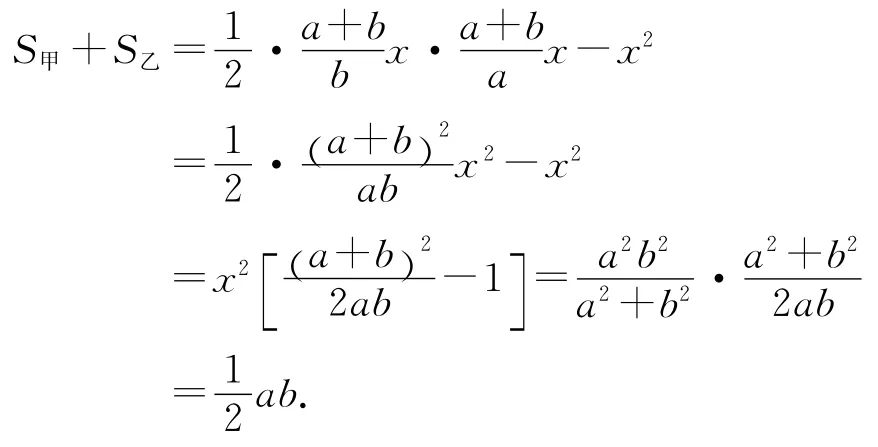
注此方法用大三角形的面积减去正方形的面积，其中依然要用到正方形的边长x的值.

解法6二倍角公式

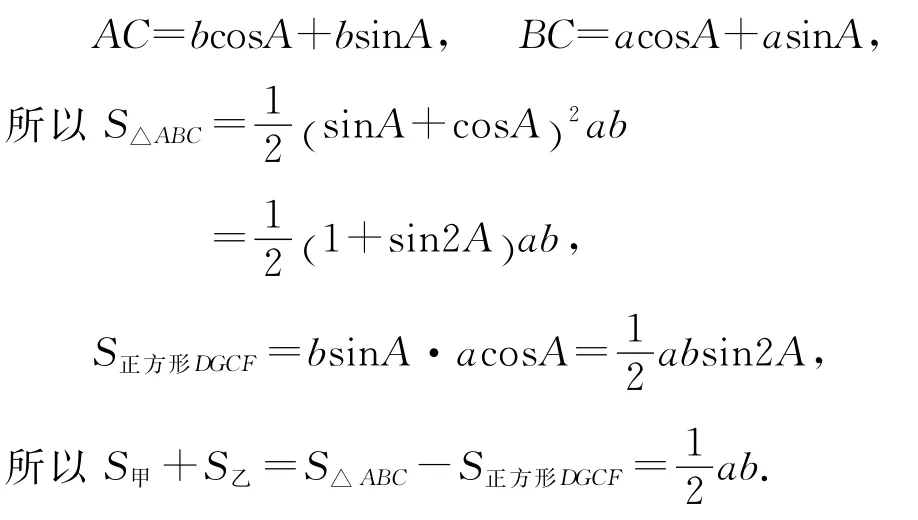
注此法先由两三角形相似，得到∠FDB=∠A，再根据二倍角公式即可求出结果，通俗易懂，简单明了.

解法7向量法

注此向量法体现了数学中的简洁美，优点在于两条线段平行时，线段之积即可转化为向量之积，然后再由两垂直向量之积为0及向量的运算即可化简成两平行向量之积，最后转化为线段之积，顺利求解.但是此方法有一定的技巧性，思维逻辑型强.

解法8无字证明

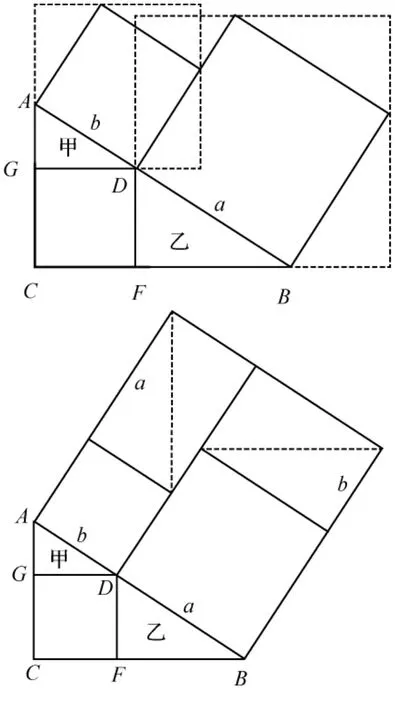
图9

如图9中，上边4个小直角三角形围成的正方形与四个大直角三角形围成的正方形面积之和等于下边大正方形的面积.都减去边长分别为a、b的正方形的面积，可得

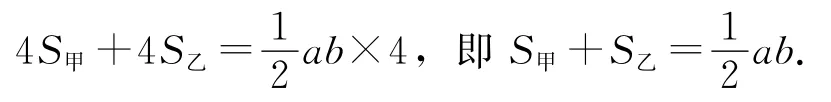
注勾股容方中，求两个小三角形面积的和，曾出现在小学毕业考试与中考试题中，因此，有必要进行研究，况且在此过程也与正方形的面积相关.

方法总结：本题的方法比较多，归纳如下：

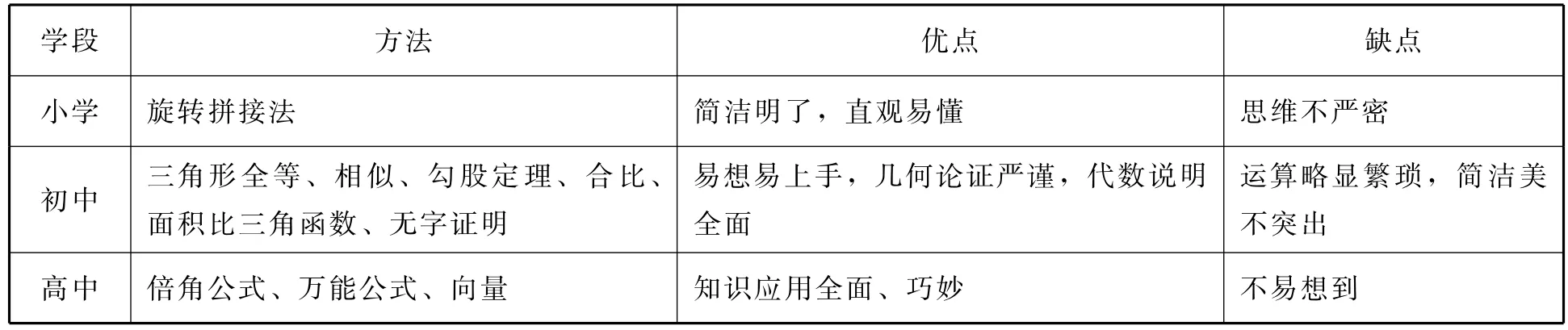
直观易懂 思维不严密初中 三角形全等、相似、勾股定理、合比、__________面积比三角函数、无字证明学段 方法 优点 缺点小学 旋转拼接法 简洁明了，不突出________________高中 倍角公式、万能公式、向量 知识应用全面、易想易上手，几何论证严谨，代数说明全面___________________________________运算略显繁琐，简洁美巧妙 不易想到

扩展

1.如图1，已知正方形GCFD的边长为a，若点A在CG延长线上运动，直线AD交CF延长线于B，是否存在S△ABC的最值，是最大值还是最小值？

解析设AG=x，因为，

所以存在S△ABC的最小值，此时△ABC为腰长为2a的等腰直角三角形，如图10所示.

图10

注本题和前面的题型相反，此类经常出现在高中数学试卷中，已知正方形来探究外接直角三角形的最值问题，同时也是动点问题，先利用相似，再利用不等式的基本性质即可解决，展示了逆向思维及由一般到特殊的思想方法.

2.（2011年全国初中数学联赛试题）如图1，已知在直角三角形ABC中，斜边AB的长等于35，正方形DGCF内接于三角形ABC，且其边长为12，求三角形ABC的周长.

解法1

设BC=a，AC=b，可得，

即ab=12（a+b）.

又由a2+b2=352，

可得（a+b）2-24（a+b）=352，

所以（a+b-49）（a+b+25）=0，

解得a+b=49，a+b=-25（舍去），

所以三角形ABC的周长是49+35=84.

解法2

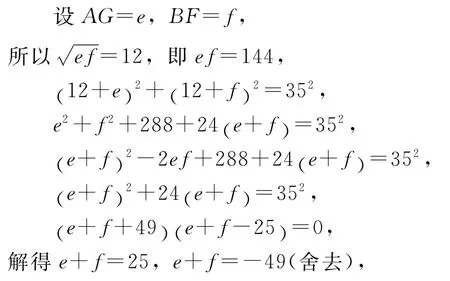
所以三角形ABC的周长是25+12+12+35=84.

注 本题是利用整体的思想，分别根据设的不同，求出相应两条线段的和，进而求出三角形的周长.

勾股容方给我们的思考

1.题目的美感.题目由三个相似的直角三角形和一个正方形构成，恰好正方形的边长又把这三个直角三角形紧密连接一起，图形中各线段彼此相关，牵一而动十，而图形的特殊情形则是三个全等的等腰直角三角形和一个正方形，给人一种直观的、让人爱不释手的美感.

2.可对勾股容方进行变式，（1）条件不变，已知勾股，还可以求两个小三角形的边长及面积等.（2）条件改变，也可以求出正方形的边长.（3）条件改变，还可以探究许多结论，如求出两个小三角形的面积.

3.综合来看，勾股容方问题及拓展，可直接求、间接求、转化求，可培养中小学生的核心素养，东北师范大学史宁中教授指出的“用数学眼光观察世界，用数学思维分析世界，用数学语言表达世界.”在此得到了体现，要加强知识的纵横联系（纵向，从大方面来说就是从中小学各学段来寻求解决问题的策略，横向，即选用代数、几何等不同的方法），提高学生的解题能力.曾培养出普通中学一个班55%的学生考进清华、北大的特级教师孙维刚指出，数学要力求达到一题多解，从不同的角度用不同的方法去解决问题，进而多解归一，寻求不同解法之间的共性.

4.日本数学家米山国藏说过：在学校学的数学知识，毕业后若没什么机会去用，一两年后，很快就忘掉了.然而，不管他们从事什么工作，唯有深深铭刻在心中的数学的精神、数学的思维方法、研究方法、推理方法和看问题的着眼点等，却随时随地发生作用，使他们终生受益.我们数学老师要做的就是通过数学史培养学生的爱国热情、热爱数学的兴趣及解决数学问题的能力，并且这种能力在以后也能去解决学生在成长道路上遇到的各种问题.