1720号问题的极点、极线结构

李伟健

（安徽省滁州中学，239000）

文[1]提出的1720号数学问题内容如下：△ABC中，以BC为轴（长轴或短轴均可）作一椭圆交AB于E，交AC于F.设M、N分别是点E、F关于直线BC的对称点，EN交FM于D.求证：AD⊥BC.文[2]给出了证明方法，之后文[3]、文[4]进行了大篇幅的讨论分析，得出的结论极富美感，但两者推理过程由于计算过于繁琐而稍显不和谐，笔者从极点、极线出发简化文[4]的证明；另外文[4]对文[3]的推广工作并不彻底，本文对文[4]补充完善，并彻底推广了文[3]的工作；此外，回归原问题，在思考1720号问题的结构过程中，得到了一个有趣性质，并以此为基础，解释了文[5]作者赵忠华老师利用几何画板发现的一个有趣现象.

1 文[4]推理过程的简化

文[3]对1720号问题开展分析讨论，得出两个结论，即为：

结论1以△BC中的BC为长轴（实轴）的椭圆（双曲线）交此三角形的另两边AB、AC分别于点E、F.设M、N分别是点E、F关于直线BC的对称点，G、H分别是E、F在x轴上的射影，连EN交FM于D，连EH交FG于K，连BF交CE于Q，过点E、F分别作椭圆（双曲线）的切线交于点P，则A、P、Q、K、D五点共线.

文[4]同样对数学问题17 20试图对结论1进行推广，探究得到的4个结论，概括地来说，即为如下结论：

结论2设A，B，C，D是非退化二阶曲线Γ上不同的四点，连直线AC、BD交于点M，连直线AD、BC交于点N，过点A，B分别作曲线Γ的切线交于点P，过点C，D分别作曲线Γ的切线交于点Q.则M、N、P、Q四点共线.

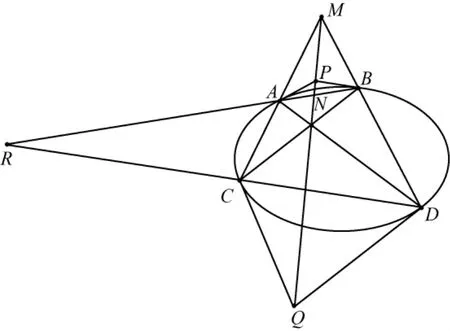
该结论具有和谐的美感，不足之处在于论证过程过于繁琐而失去美感，本文从极点与极线的角度，结合配极原理，予以论证，即：

证明记R=AB×CD，由于MNR是自极点三点形，直线MN为R的极线，因为PA，PB与Γ相切于点A，B，所以直线AB是P点的极线，且经过点R，根据配极原理，点R的极线必过点P，同理直线MN也过点Q，即M、N、P、Q四点共线.

2 文[3]工作的彻底推广

文[4]所得结论较文[3]来说，另一个不足之处在于，与文[3]相比，丢失了两个点，实际上P、Q两点在结论2中情形是一样的，本文拟弥补缺失的两个点，要想补出这两个丢失的点，必须了解此两点的由来，文[3]中直线EM与直线FN，交于无穷远点，此点在位于R的极线MN上，至此，E、M与F、N的由来实际上是过R的极线上一点与曲线Γ的交点，接下来，就可以把文[4]迷失的两点再现出来，即：

结论3设L为R的极线上一点，过L作两条直线，分别交Γ于点E、M，F、N，且D=EN×FM，K=GF×EH，则D、K在R的极线上.

证明根据完全四点形MNF E的调和性，D必在R的极线上，且（RT，E F）=-1，（RD，HG）=-1，所以（R，T，E，F）（R，D，H，G），又因为公共点R自对应，所以（R，T，E，F）（R，D，H，G），所以直线DT、HE、GF三点共线，即为K在R的极线上.

行文至此，在结论[2]、[3]的基础上，文[3]所得的结论1彻底推广后的一般情形如下：

定理设B、C、E、F是非退化二阶曲线Γ四点，设A=BE×C F，Q=BF×CE，点P是曲线Γ在E、F处切线的交点，L为直线A Q上一点，直线LE、LF与曲线Γ另一交点分别为M、N，且D=EN×FM，G=BC×EM，H=BC×FN，K=GF×EH，则A、P、Q、K、D五点共线.

注文[3]实际上是L为无穷远点的特殊情形.

3 1720号问题的结构

反思文[4]的简化证明过程，实质上揭示了17 20号问题结构实质上是极点、极线.直线MN为R的极线紧紧依赖于完全四点形ABCD内接于Γ这一事实，正是这一点导致M、N、P、Q四点共线，因此说这一结果是平凡的，通过对“完全四点形ABCD内接于Γ”这一条件思考，笔者发现，完全四点形ABCD未必需要四点A，B，C，D均与Γ接触，事实上有两点就可以了，即：

定理设直线BC与非退化二阶曲线Γ相切于点B，直线AD与非退化二阶曲线Γ相切于点A，M=AC×BD，N=BC×AD，R=AB×CD，直线AC交Γ于另一点E，直线BD交Γ于另一点F，那么直线MN为R的极线.

证明以A、B为束心与另外四点B，E，F，A连接，由二阶曲线的基本定理知

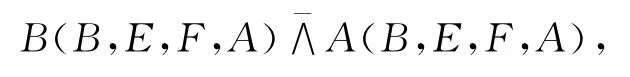
用直线AC、BD分别截以A、B为束心的线束，

则有

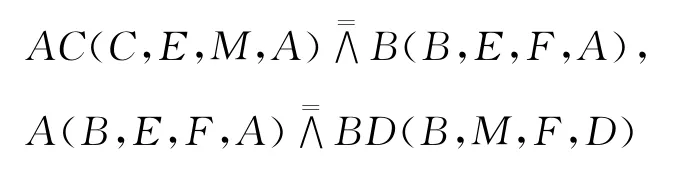
所以

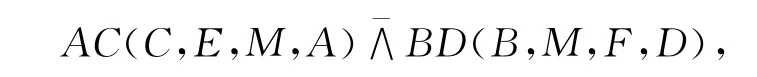
因此（CE，MA）=（BM，FD），

所以（CE，MA）=（DF，MB），

故（C，E，M，A）（D，F，M，B），

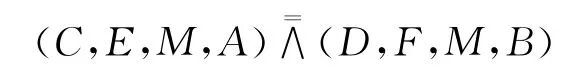
又因为两点列的交点M自对应，所以有因此DC、FE、AB三线共点，即为R.

根据完全四点形ABEF的调和性，所以点M在R的极线上，又因为R在点N的极线上，所以点N在R的极线上，所以直线MN为R的极线.

从证明过程看，DC、FE、AB三线交于点R，可以推出欧几里得几何学中难以解释的现象变得自然，如文[5]提出的如下性质，即为本文的推论，即：

推论1在双曲线所在的平面内任取一点（该点不在渐近线和双曲线上），过此点作两条渐近线的平行线，则这两条直线与双曲线交于两点，与渐近线交于两点，则双曲线上两点连线平行于渐近线上两点连线.

这一结论放到射影空间内就好解释了，双曲线的渐近线实际上是其与无穷远直线交点处的切线，为了便于解释，如图所示：

双曲线上两点连线FE，渐近线上两点连线DC交于无穷远点R∞，所以二者必然平行.

注该结论属于赵忠华老师.

从证明的结果看，直线MN为R的极线，设I=AG×BH，J=F G×EH，则有如下：

推论2M、N、I、J四点共线，此线就是R的极线，也是曲线Γ的Pascal线.

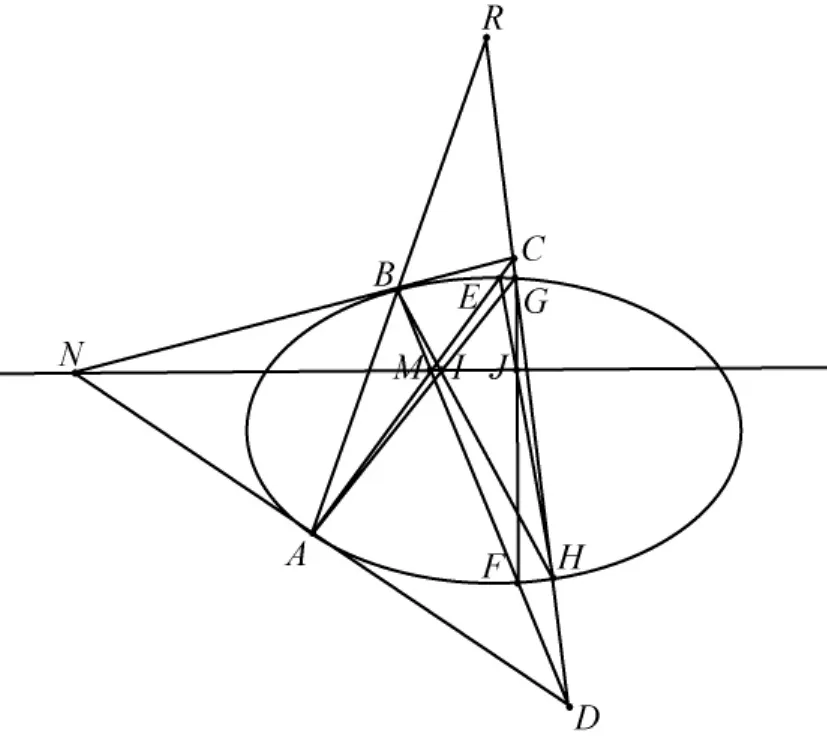
注这一图形蕴藏着大量的共线点，有兴趣的读者不妨一试.