函数应用题分类解析
朱干江●
江苏省盐城市第一中学(224005)
函数应用题分类解析
朱干江●
江苏省盐城市第一中学(224005)
应用题是历年高考命题的主要题型之一,而函数应用题又是历年高考的热点之一.解答函数应用题,一般都是从建立函数解析式入手,将实际问题数学化,并在其定义域内给出完整、准确的解答. 本文拟介绍几种常见的函数应用题题型,供同学们复习时参考.
一、一次函数模型
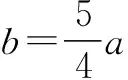
点评 本题考查一次函数的应用,要注意找好题中的等量关系:新价让利总额=新价×20%×售出件数,然后根据等量关系列出函数关系式即可.由实际问题建立的函数关系式,它的定义域除受其解析式的约束外,还要受到问题中变量的实际意义等具体条件的约束,本题的定义域为x∈N*).
二、二次函数模型
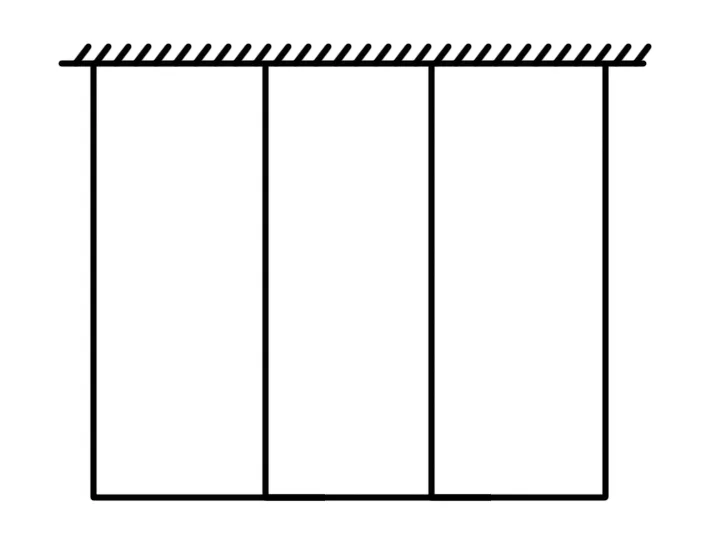
例2 有一批材料可以建成200 m的围墙,如果用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图所示),则围成的矩形最大面积为____(围墙厚度不计) .
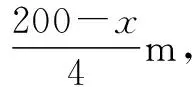
点评 构造二次函数模型,函数解析式求解是关健,然后利用配方法、数形结合法等方法求解二次函数的最值,但要注意自变量的实际取值范围.
三、指数或对数函数模型
例3 为救助失学儿童,鲁能泰山足球俱乐部准备在山东省体育中心体育场举行一场足球义赛,预计卖出门票2.4万张,票价有3元、5元和8元三种,且票价3元和5元的张数的积为0.6万.设x是门票的总收入,经预算,扣除其他各项开支后,该俱乐部的纯收入函数为y=lg2x,当为失学儿童募捐纯收入最多时,a=____,b=____,c=____.
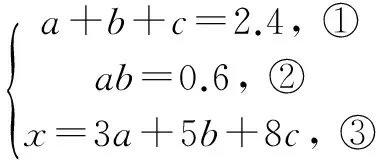

(1)信息采集模块。该模块主要完成对有效信息的采集,在主题爬虫中关键是设定一些网站的相关信息、有效信息的抓取方式和条件,并规划主题爬虫的搜索路径。
由于y=lg2x为增函数,故当a=0.6,b=1,c=0.8时,y=lg2x恰有最大值. 故三种门票分别为0.6、1、0.8万张时为失学儿童募捐纯收入最多.
点评 该函数模型y=lg2x已给定,因而只需要将条件信息提取出来,按实际情况代入,应用于函数即可解决问题.解指数或对数函数应用题必须掌握指数、对数运算以及指数、对数函数的性质,还要熟练应用近似计算的知识进行估算.
四、分段函数模型
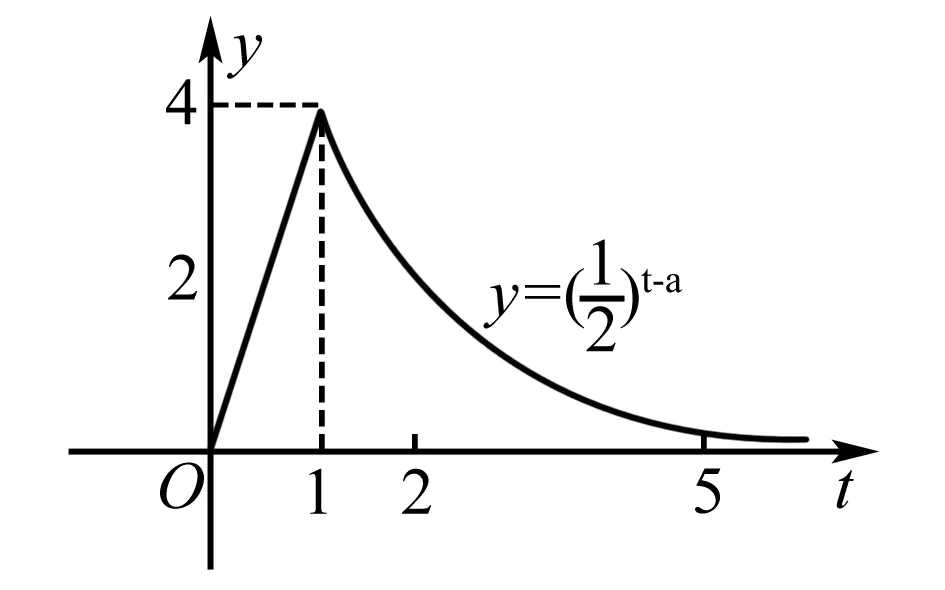
例4 某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.①则第一次服药后y与t之间的函数关系式y=f(t)=____.②据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗有效.则服药一次后治疗有效的时间是____小时.
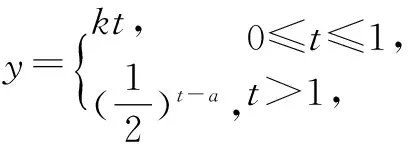
点评 题中图象本来是通过实验分析得到相关数据抽象出来的数学模型,这里让我们通过识图找到相应的函数关系式,然后建立每毫升血液中的含药量关于时间的分段函数. 分段函数主要是每一段自变量变化所遵循的规律不同,可以先将其当作几个问题,将各段的变化规律分别找出来,再将其合到一起,要注意各段自变量的范围,特别是端点值.
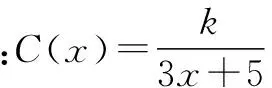
六、高次函数模型
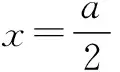
(1)求y=f(x)的解析式及定义域;
(2)求出产品的增加值y的最大值及相应的x值.
解析 (1)由已知,设y=f(x)=k(a-x)x2.
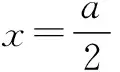
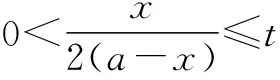
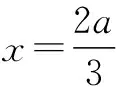
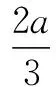
点评f′(x0)=0,只是函数f(x)在x0处有极值的必要条件,求实际问题的最值应先建立一个目标函数,并根据实际意义确定其定义域,然后根据问题的性质可以断定所建立的目标函数f(x)确有最大或最小值,并且一定在定义区间内取得,这时f(x)在定义区间内部又只有一个使f′(x)=0的点x0,那么就不必判断x0是否为极值点,取什么极值,可断定f(x0)就是所求的最大或最小值.
七、识图型应用题
例7 下图中的阴影部分由底为1,高为1的等腰三角形及高为2和3的两矩形所构成.设函数S=S(a)(a≥0)是图中阴影部分介于平行线y=0及y=a之间的那一部分的面积,则函数S(a)的图象大致为( ).
解析 根据图象可知在[0,1]上面积增长的速度变慢,在图形上反映出切线的斜率在变小;在[1,2]上面积增长速度恒定,在[2,3]上面积增长速度恒定,而在[1,2]上面积增长速度大于在[2,3]上面积增长速度,故选C.
点评 本题主要考查了函数的图象,同时考查了识图能力以及分析问题和解决问题的能力.先观察原图形面积增长的速度,然后根据增长的速度在图形上反映出切线的斜率进行判定即可.
G632
B
1008-0333(2016)34-0002-02

