巧用万有引力定律,越过天体运动鸿沟
周宏建●
江苏省江安高级中学(226534)
巧用万有引力定律,越过天体运动鸿沟
周宏建●
江苏省江安高级中学(226534)
万有引力定律在天体运动中的体现是最为重要最为直观的,我们需要有良好的基础知识以及一定的灵活思维才能更好的解决此类问题.通过万有引力的相关知识与圆周运动相结合,使天体运动变成圆周运动与受力分析等多种知识相互联系的重要知识点,本文中通过对三中不同情况下的天体运动进行举例分析,帮助学生更准确更全面的分析此类问题.
一、抓准特殊位置,玩转卫星变轨
常见的卫星变轨最多为3个轨道间的互相改变,轨道间的相切点就是我们重点研究的对象,多点的速度以及加速度间的互相比较是容易混淆的物理量,学生需要能清晰地分析判断.
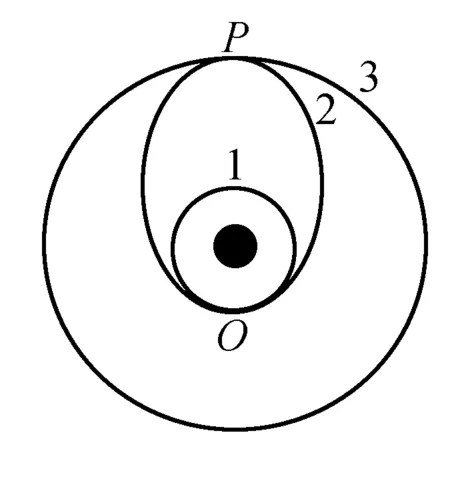
图1
例1 如图1所示,发射卫星时通常有三个轨道,近地圆轨道1,椭圆轨道2,最终圆轨道3.先将卫星发射至轨道1,然后经点火,使其沿2运行,最后再次点火,将卫星送入3.轨道1、2相切于Q点,2、3相切于P点,则以下说法正确的是( ).
A.卫星在轨道2上运动的周期大于它在轨道3上运动的周期
B.卫星在轨道3以及轨道2上分别经过P点时的速度相等
C.卫星在轨道3上的速率大于在轨道1上的速率
D.卫星在轨道1以及轨道2上分别经过Q点时的加速度相等
解析 本题中涉及周期、速度、加速度等多个物理量,在这里将需要注意的点逐一说明.对于匀速圆周运动才存在万有引力提供向心力,即将圆周运动的各种公式代入至此.而天体运动中最为特殊的就是加速度问题,加速度是完全由万有引力提供的,与其是否是匀速圆周运动无关.对于A中的周期,我们可以利用开普勒第三定律,轨道2上的半长轴小于3上的半径,故在轨道2上的周期小于轨道3上的周期.对于B,在轨道2上的P点是做近心运动,故在轨道2上P点的速度不足以满足在轨道3上做匀速圆周运动的速度,才会出现此种情况.对于C,就是常见的不同位置的速度大小的比较,轨道1上的线速度要比轨道3大.而D就是前面提到的只要是同一点,两者的加速度就相等.因此选择D.
二、灵活转变思维,攻破天体相遇
在这里相遇并不是指两颗天体相撞,是指两个天体距离最近的状态.而有最近的同时也会有最远状态,在圆形轨道中确认这两种状态的问题是很容易的,我们需要在找出状态之后进行相关的时间等物理量的计算.
例2 如图2所示,有A、B两颗行星绕同一恒星做同方向的圆周运动,周期分别为T1、T2,在某时刻相遇(距离最近),则分别经过多久两行星又一次相距相遇以及距离最远.

图2
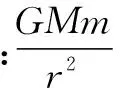
三、掌握受力分析,巧解多星问题
天体物理中存在多星的自然天文现象,在遵从万有引力定律的前提下,多星之间组成了一同做圆周运动的整体系统.其中双星问题是较为常见的,老师在讲课时也都有所涉及,下面以三星问题为例,向学生介绍此类问题的分析方法.
例3 宇宙中的三星系统有两种基本的构成情况:一种是两颗星围绕中央星体做半径为R的圆周运动如图3,三颗星位于同一直线上;另一种是三颗星位于等边三角形的三个顶点上如图4,所做的圆周运动是外接于等边三角形的圆形轨道.设每个星体的质量均为m.(其他星体的影响可忽略不计)
(1)求第一种情况下,星体运动的线速度和周期.
(2)若两种情况星体的运动周期相同,求第二种情况下各星体间的距离.
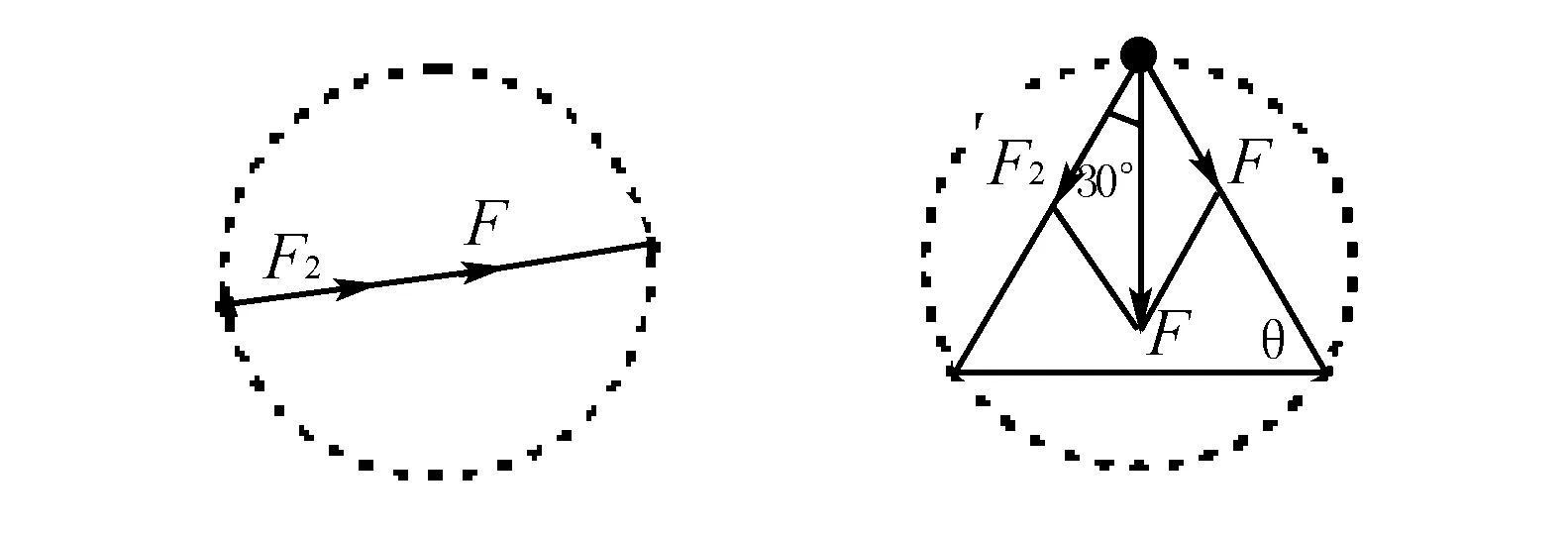
图3 图4
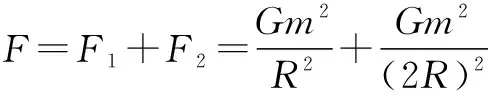
G632
B
1008-0333(2016)34-0061-01

