基于不同层级电网性能评估的投资分配方法

葛亮，徐谦，程浩忠，兰洲，柳璐

(1.电力传输与功率变换控制教育部重点实验室(上海交通大学)，上海市 200240； 2.国网浙江省电力公司经济技术研究院，杭州市 310008)

基于不同层级电网性能评估的投资分配方法

葛亮1，徐谦2，程浩忠1，兰洲2，柳璐1

(1.电力传输与功率变换控制教育部重点实验室(上海交通大学)，上海市 200240； 2.国网浙江省电力公司经济技术研究院，杭州市 310008)

考虑不同层级电网性能评估，研究电网投资分配方法。首先根据不同特点将电网划分为不同层级，并建立不同层级电网的性能指标体系；应用模糊数学综合评价方法对电网性能进行综合评估，并利用logistic曲线对电网性能与累计投资的关系进行拟合；以电网性能裕度的方差最小为目标建立投资分配模型；最后，以我国东部某省电网为算例进行验证分析，给出该省“十三五”期间不同层级电网的投资分配额，结果合理可信，验证了本文所提出的投资分配方法的可行性。

投资分配; 性能评估; 不同层级电网; logistic

0 引 言

目前，电网的建设和运营主要由电网公司负责，电网公司承担着保证电网安全和向用户提供充足可靠电能的任务，在此过程中电网的性能十分关键。电网的投资不仅要满足负荷的增长需求，还要能够提升电网性能，以此提高电网公司的服务质量；在电网投资的过程中，需要考虑不同层级电网之间的统筹协调性，保证电网整体性能的提升。因此，考虑不同层级电网性能评估的投资分配，对于抑制电网盲目投资、有效提升电网性能具有十分重要的意义。

对于电网投资，学术界的研究成果较少，文献[1-2]建立了负荷水平、电网规模、社会经济水平3个指标与电网投资之间的关系，基于灰色理论提出了一种电网投资预测方法；文献[3]研究最大负荷与电网投资之间的长期均衡关系，基于协整理论和误差修正模型建立了电网投资需求预测模型；文献[4]研究电网不同发展阶段的投资需求特性；对于投资分配，文献[5]在多个项目间进行组合投资优化；文献[6-7]在多个电网子公司之间进行投资分配。以上这些研究均未考虑电网性能与投资的关系，且没有在不同层级电网间分配投资。

目前关于电网性能的指标主要包括：安全可靠性、统筹协调性、高效经济性、环境影响性等方面[8-11]。文献[12]对输配电网分别建立了指标体系，但不同电压等级电网的特点不同，其性能指标的侧重点也必然不尽相同，需要将其归类细分，建立不同层级电网性能指标体系。因此，有必要建立不同层级电网性能指标体系并建立电网性能与投资之间的关系，建立模型对电网投资在不同层级电网间进行优化分配。

本文根据各级电网的特点，将电网划分为不同层级，分别建立不同层级电网性能指标体系；应用模糊数学综合评价方法[13]对电网进行评估，利用logistic曲线[14]对电网性能与累计投资之间的关系进行拟合；以不同层级电网性能裕度的方差最小为目标，对电网投资进行优化分配[15]。

1 不同层级电网性能指标体系

1.1 电网层级的划分

目前，电网一般根据电压等级来划分，本文考虑500 kV及其以下电网，现在电网中使用较多的电压等级有10，35，110，220和500 kV，但从各个电压等级电网的功能定位出发，可以将电网划分为35 kV及以下、110/220 kV、500 kV这3个层级。

1.2 不同层级电网性能指标

(1)35 kV及以下电网是面向用户的中低压配电网，在建立其电网性能评估指标体系时主要考虑配电网的性能指标，尤其考虑与用户相关的指标，35 kV及以下电网性能评估指标体系如表1所示。

表1 35 kV及以下电网性能指标

Table 1 Performance index of power grid below 35 kV

安全可靠性方面，中压线路互联率、电缆化率和架空线路绝缘化率与配电网的安全运行有十分密切的关系，是配电网的关键性能指标，而供电可靠率是能够直接反映配电网可靠供电的指标；统筹协调性方面，容载比过小时，可能导致配电网配电容量偏小，威胁到配电网充足供电和安全运行的能力，容载比过大时，大量配电站和配电设备的投入将导致电网利用率降低；高效经济性方面，网损率是表征电网经济运行的重要性能指标；环境影响性方面，配电网中接入分布式能源将对电网和环境产生一定的影响，分布式能源接入比例是评估现代配电网时必须考虑到的重要指标。

(2)110/220 kV电网是电网的中间层级，功能处于输电网和配电网之间，在建立其电网性能评估指标体系时要兼顾输电网和配电网的特点，110/220 kV电网性能评估指标体系如表2所示。

表2 110/220 kV电网性能指标

Table 2 Performance index of 110/220 kV power grid

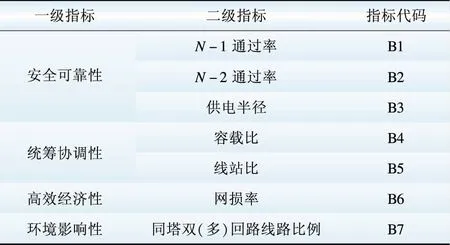
安全可靠性方面，N-1通过率和N-2通过率是表征输电网安全可靠性能的主要指标，供电半径由变电站座数决定，也是表征电网供电可靠性的重要性能指标；统筹协调性方面，容载比依然是重要的性能指标，同时，线站比作为线路与变电站之间的协调性指标，也是110/220 kV层级电网重要的性能指标；高效经济性方面，网损率是表征电网经济运行的重要性能指标；环境影响性方面，考虑节约土地的因素，将同塔双(多)回线路比例作为表征该层级电网对环境影响的性能指标。

(3)500 kV电网作为超高压网架，远距离输送大量电能，在建立其电网性能评估指标体系时要着重考虑安全可靠性方面的性能，其性能评估指标体系如表3所示。

表3 500 kV电网性能指标

Table 3 Performance index of 500 kV power grid

安全可靠性方面，除了110/220 kV层级电网性能中的N-1通过率、N-2通过率和供电半径外，还增加了平均容性补偿百分比和按暂稳控制线路占比，无功补偿和线路稳定问题对于500 kV电网尤为重要；其他3个方面与110/220 kV电网性能指标一致，均考虑了容载比、线站比、网损率和同塔双(多)回线路比例。

2 电网性能综合评估

2.1 模糊隶属度计算

本文采用模糊数学综合评估方法对电网的性能进行评估，由于各个指标的量纲不同，数值大小也参差不齐，为了能够将各个指标融合到最后的综合评价结果中，需要把各个指标统一到同一个量纲，并将其数值统一至0～1，因此引入模糊隶属度函数对各个指标进行拟合，通过各自的模糊隶属度函数计算得到该指标的模糊隶属度，这个过程的实质就是对每个指标值的好坏进行单独评价。

本文采用应用较为广泛的梯形分布线性隶属度函数来进行计算，需要根据各个指标的不同特性将指标分为正指标、逆指标和适度指标3类。正指标的数值越大越好，逆指标则与正指标相反，而适度指标的数值需要控制在一定范围内，过大或过小都会影响电网性能，因此这3类指标所选用的隶属度函数类型也有所不同，具体如下所述。

(1)正指标，采用升半梯形分布函数：

(1)

式中a1和a2分别是分布函数自变量的下限和上限。

(2)逆指标，采用降半梯形分布函数：

(2)

(3)适度指标，采用梯形分布函数：

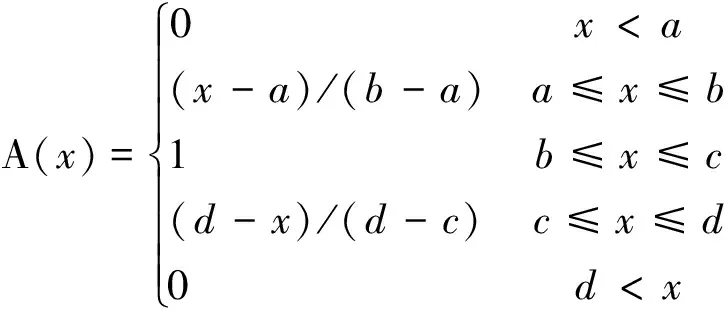
(3)

式中：a和d分别是变量的下限和上限；b和c分别是区间的两端值。

正指标以期望能够达到的最大值为分布函数自变量的上限，以0或者标准规定的不能接受的值为分布函数自变量的下限；逆指标以0或者期望能够达到的最小值为分布函数自变量的上限，以标准规定的不能接受的值为分布函数自变量的下限；适度指标以标准规定的适用值为分布函数自变量最佳区间的两端值，以最不理想情况下指标的可能值为分布函数自变量的上下限。

不同电网性能指标根据其各自的特性构造不同的模糊隶属度函数，其中的上下限参数根据指标各自的实际情况而设定。本文选取的电网性能指标的分类如表4所示。

表4 电网性能指标分类

Table 4 Classification of power grid performance index

2.2 指标赋权

在对电网性能进行综合评价时，需要确定各个指标的权重系数，即各个指标对综合评价结果的影响程度。目前赋权方法主要分为主观赋权法和客观赋权法，其中主观赋权法在赋权过程中存在主观因素对赋权结果的影响。因此，为了消除主观因素的影响，本文采用多种客观赋权法相结合的组合赋权法。

2.2.1 变异系数法

变异系数法根据某个指标在所有评价对象中数值的变异程度来确定该指标的权重系数，本文采用标准差作为变异系数进行赋权，计算步骤如下所述。

假设共有n个电网性能指标，q个评价对象。

(1)计算各指标的标准差系数Kj

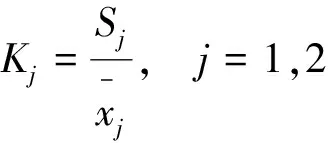
(4)

(2)对各指标的变异系数进行归一化处理，得到变异系数法权重wj,1

(5)

2.2.2 熵值法

指标熵值越小，其中包含的信息越多，相应的该指标的权重越大，其计算步骤如下所述。

假设共有n个电网性能指标，q个评价对象。

(1) 为了避免计算过程中出现无意义的现象，首先需要将指标值非负化处理，非负化公式如下：

(6)

式中：xij为第i个评价对象第j项指标的数值；min(xij)和max(xij)分别为第j项指标的最小值和最大值；yij为xij非负化后的指标值。

(2)计算第i个评价对象第j项指标yij在所有第j项指标中所占的比重pij：

(7)

(3)计算各项指标熵值并归一化：

(8)

当所有指标pij相等时，熵值最大且为lnq，归一化后得到表征指标j相对重要性的熵值Ej：

Ej=ej/lnq， j=1,2,...,n

(9)

式中q为评价对象个数。

(4)由于熵值越小，变异程度越大，因此第j项指标的熵值法权重wj,2如式(10)所示：

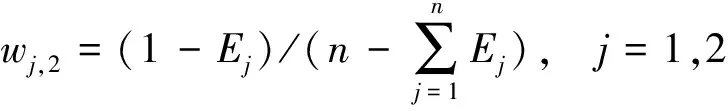
(10)

式中n为指标个数。

2.2.3 组合赋权法

变异系数法和熵值法运用不同的角度和计算方法对指标进行赋权，得到的各指标权重系数稍有差异，运用组合赋权方法将不同赋权方法得到的权重综合起来，兼顾了不同赋权方法的不同角度和优劣，使指标的权重系数更加科学合理并符合实际。

常用的组合赋权方法可以归结为“加法”集成法和“乘法”集成法，本文采用后者中的简单平均算法作为组合赋权方法，即

(11)

2.3 模糊合成

目前应用较为广泛的模糊合成方法主要有“加权平均型”和“主因素突出型”两大类，考虑到本文中电网性能评价体系的特点和运算的便捷性，本文采用“加权平均型”中的普通乘与加算子，即：

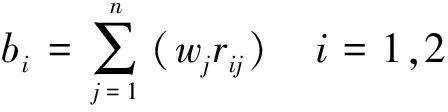
(12)

式中：bi为第i个评价对象的综合评价分值；wj为第j项指标的权重系数；rij为第i个评价对象的第j项指标的模糊隶属度。

3 电网投资分配方法

3.1 电网综合性能与投资的关系

随着电网负荷的增长，电网公司需要新建变配电站和输配电线路来提高电网的供电能力，以此满足电网用户的用电需求。电网发展初期，电网综合性能处于较低的水平，电网基础设施也不够完善，电网投资的主要目的是完善电网基础，电网综合性能随累计投资的增长速度较慢。随着电网发展到中期阶段，电网拥有一定的基础，此时电网投资除了能够满足负荷增长外，还能有效地提高电网的综合性能，电网综合性能随累计投资的增长速度较快。当电网发展到后期阶段，随着电网规模越大，提升电网综合性能的难度越高，即提高相同电网综合性能时需要投入的资金越多，而随着累计投资的增加，电网综合性能将呈现趋于饱和的状态，因此，可以采用logistic曲线模型来拟合电网综合性能与累计投资之间的数学关系。

应用第2节所述的模糊数学综合评估方法对不同层级电网的性能进行综合评估，利用logistic曲线对电网性能综合评分和累计投资的关系进行拟合，得到不同层级电网性能综合评分关于累计投资的数学关系表达式。

3.2 电网投资分配模型

为优化电网建设投资，达到不同层级投资性能收益均衡，不同层级电网均衡全面发展，避免投资分配不均而导致某个层级电网建设落后，考虑优化目标为不同层级电网性能综合评分裕度的方差最小，即：

(13)

(14)

(15)

约束条件为：

x1+x2+x3=X

(16)

d1,d2,d3≥0

(17)

式中：x1、x2、x3分别为不同层级电网的建设投资额；X为总投资额；c1、c2、c3分别为基于国标、行标、企标约束的不同层级电网性能评分最低标准值，同样可以通过模糊数学综合评估方法得到；f1(x1)、f2(x2)、f3(x3)分别为不同层级电网性能综合评分与累计投资之间的数学关系表达式。

4 算例分析

采用我国东部某省电网作为算例对本文提出的基于不同层级电网性能评估的投资分配方法进行验证分析。以1991年至2015年该省电网为评价对象，应用模糊数学综合评价方法分别对35 kV及以下电网、110/220 kV电网、500 kV电网3个不同层级的电网进行性能综合评估；利用logistic曲线对不同层级电网性能综合评分与累计投资的关系进行拟合；最后利用本文提出的投资分配模型，求解该省“十三五”期间不同层级电网投资分配额。

4.1 不同层级电网性能评估

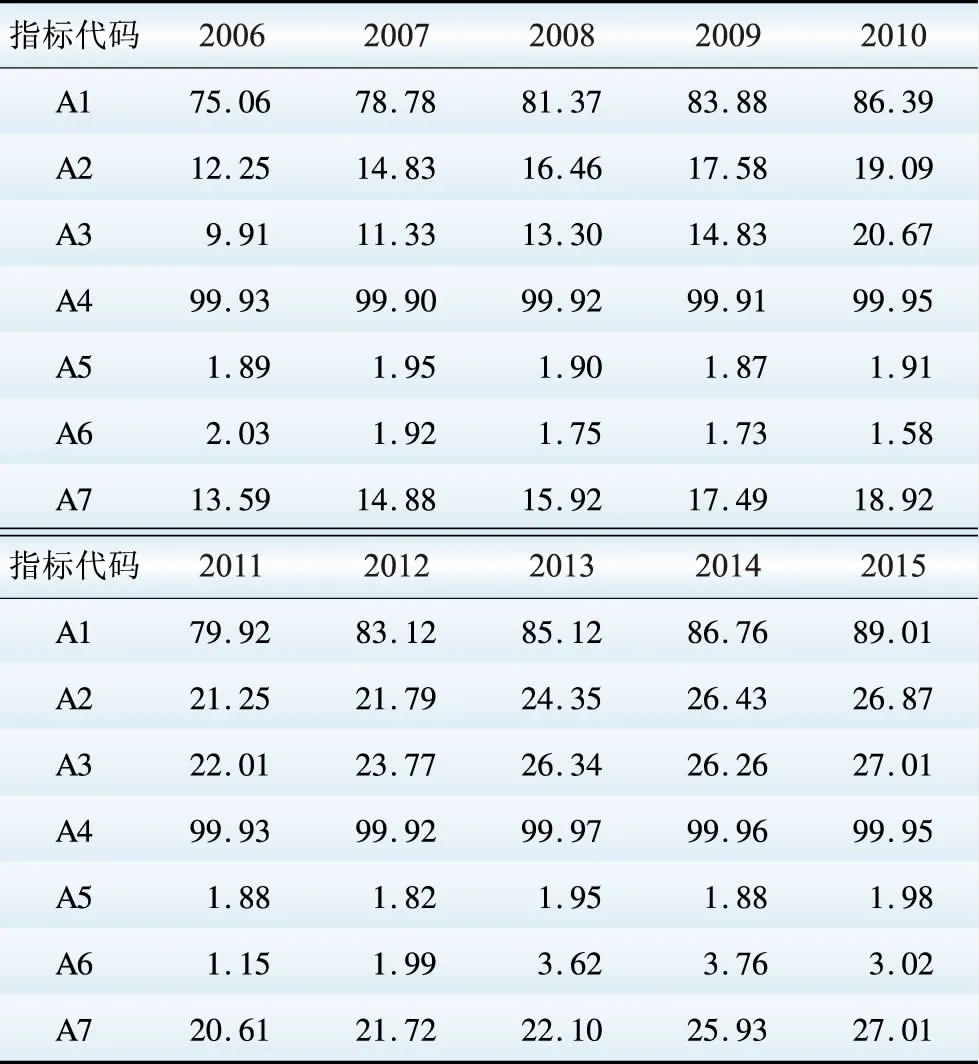
以35 kV及以下电网为例，给出电网综合性能评估的计算过程，其中2006年至2015年35 kV及以下电网各指标值如表5所示。

表5 35 kV及以下电网性能指标值

Table 5 Value of performance index in

power grid below 35 kV

根据表5中对各个指标的分类及自身数据特性，分别设置各指标的梯形分布线性隶属度函数并计算隶属度，结果如表6所示。

利用2.2节中综合了变异系数法和熵值法的组合赋权法，对不同层级电网的各个指标进行赋权，结果如表7所示。

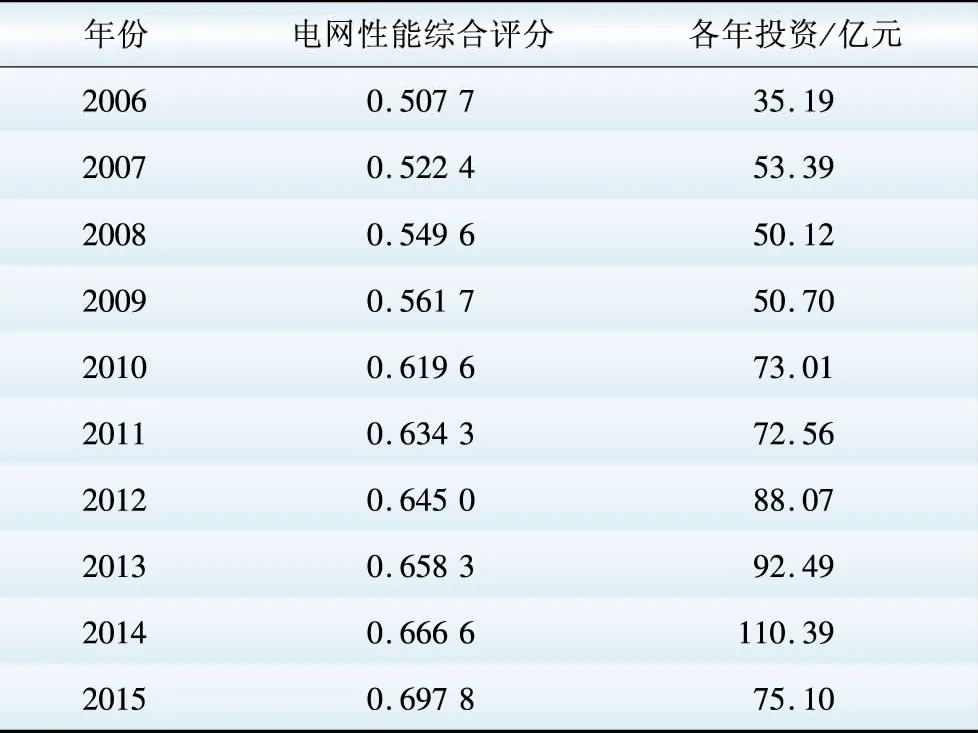
得到各指标的隶属度和权重后，利用式(12)通过简单乘与加模糊合成算子计算得到各年电网性能综合评价分值，计算结果及各年投资情况如表8所示。

表6 35 kV及以下电网性能指标隶属度

Table 6 Membership degree of performance index in power grid below 35 kV

表7 35 kV及以下电网性能指标权重

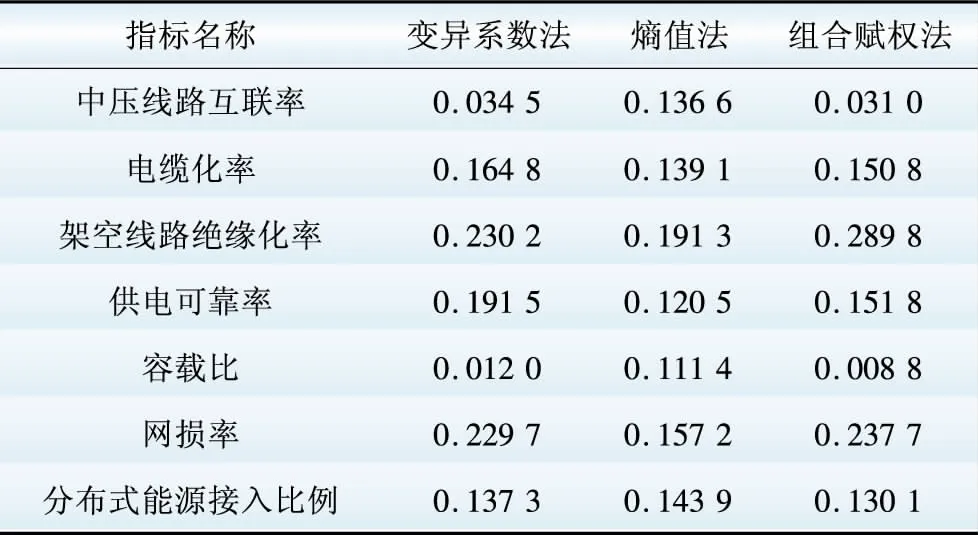
表8 35 kV及以下电网性能综合评分及投资额

对于另外2个层级电网的计算与以上过程类似，得到的结果如表9—12所示。

表9 110/220 kV电网性能指标权重

Table 9 Weight of performance index in 110/220 kV power grid

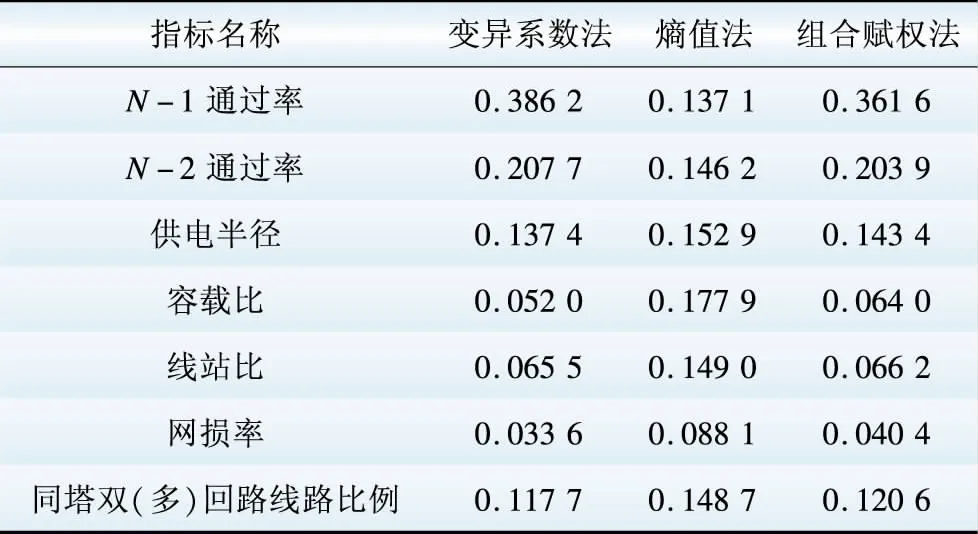
表10 110/220 kV电网性能综合评分及投资额

表11 500 kV电网性能指标权重

4.2 电网综合性能与投资的关系

利用logistic曲线对不同层级电网的性能综合评分与累计投资的数学关系进行拟合。考虑到电网投资首先需要满足负荷的增长，负荷增长较快的情况下，电网性能的提升较为缓慢；而负荷增长缓慢的情况下，电网性能的提升较快。因此将不同负荷增长率划分为0%～5%、5%～10%、10%～15%、15%～20%，

表12 500 kV电网性能综合评分及投资额

Table 12 Comprehensive score of performance and investment of 500 kV power grid

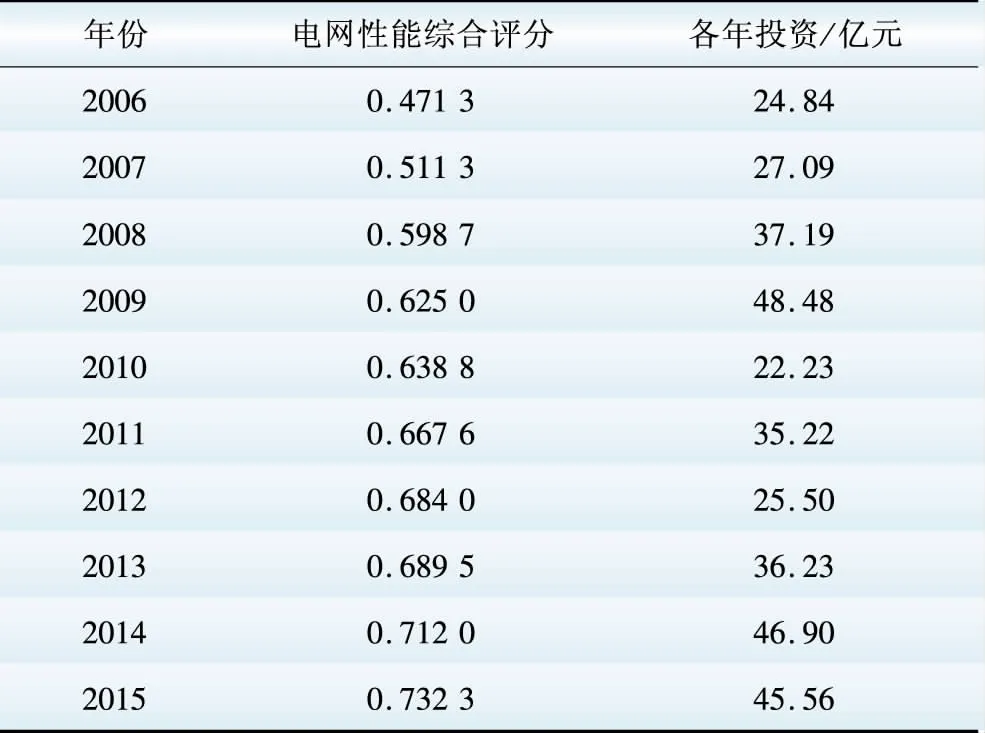
分别对不同负荷增长率情况下电网性能综合评分与累计投资的关系进行logistic曲线拟合，各个曲线的拟合度均在0.95以上，电网综合性能随累计投资的增长趋势基本符合logistic曲线。

为了便于比较和计算，将不同增长率下的曲线平移至2015年该层级电网所处的电网性能评分处，并以此为投资累计起点，不同层级电网在不同负荷增长率下性能综合评分与累计投资的关系如图1—3所示。

图1 35 kV及以下电网性能与投资的关系

由图1—3可以看出，负荷增长率越高，电网性能随投资的提升速度越缓慢，这与实际情况相符；同时，35 kV及其以下电网与500 kV电网正处于性能随着投资快速提升的阶段；而110/220 kV电网已经处于电网发展中后期阶段，电网性能的提升速度开始变慢；这与该省先前大力建设110/220 kV电网的实际情况相符。

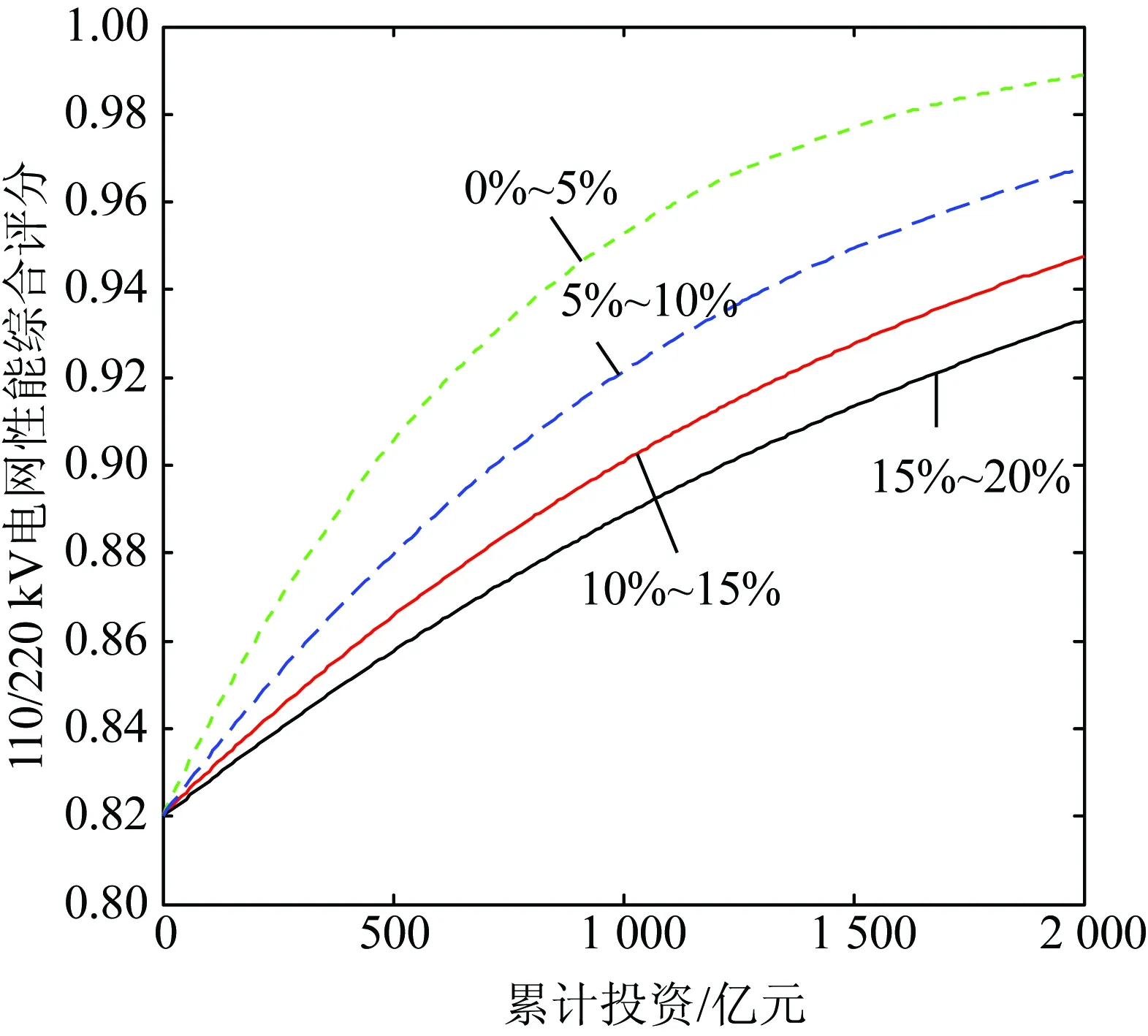
图2 110/220 kV电网性能与投资的关系

图3 500 kV电网性能与投资的关系

4.3 电网投资分配

根据该省“十三五”规划报告显示，该省在“十三五”期间的负荷平均增长率在0%～5%之间，且“十三五”期间对500 kV及以下电网的规划投资额为 1 102亿元。35 kV及以下电网、110/220 kV电网、500 kV电网在负荷增长率为0%～5%时电网性能综合评分与累积投资的数学关系式如下所示：

(18)

(19)

(20)

根据国标、行标、企标中对各个指标的规定以及本文计算得到的各指标的权重系数，可以得到35 kV及以下电网、110/220 kV电网、500 kV电网的性能综合评分最低标准值c分别为0.272 5、0.328 0、0.307 5。

以此为边界条件，利用基于淘汰相似结构机制的改进小生境遗传算法对3.2节中的投资分配模型进行求解，得到的结果如表13所示。

表13 不同层级电网“十三五”投资额

Table 13 Investment of different levels of power grid during “13th Five-Year plan” period

由此结果可以发现，对于35 kV及以下电网和110/220 kV电网的投资额相当，各自占了总投资额的40%，这与该省即将大力提升配电网性能的规划目标以及正在大力建设110/220 kV电网的举措一致；与规划投资额相比较，可以看出本文得到的投资额与规划投资额相近，结果合理可信，本文提出的基于不同层级电网性能评估的投资分配方法合理可行。

5 结 论

本文提出了基于不同层级电网性能评估的投资分配方法，建立不同层级电网性能指标体系，以我国东部某省电网为算例，运用模糊数学综合评估方法对电网性能进行综合评估，得到各个指标的权重系数；利用logistic曲线对电网性能与累计投资之间的关系进行拟合，同时分析了负荷增长率对电网性能提升的影响；最后，建立了以不同层级电网性能裕度的方差最小为目标的投资分配模型，利用基于淘汰相似结构机制的改进小生境遗传算法对模型求解得到“十三五”期间不同层级电网投资额。算例结果合理可信，验证了该方法的可行性，对电网投资规划有一定的参考意义。

[1]胡柏初, 胡刚, 胡朝华，等. 基于灰色预测的电网基建投资测算模型[J]. 电子科技大学学报,2013,42(6):890-894.

HU Baichu, HU Gang, HU Chaohua, et al. Grid infrastructure investment calculation model based on gray prediction[J]. Journal of University of Electronic Science and Technology of China, 2013,42(6): 890-894.

[2]魏子杰. 基于灰色理论的电网投资测算方法研究及软件实现[D].成都：电子科技大学,2013.

WEI Zijie. Graytheory based research and software implementation of power grid investment measure method[D]. Chengdu: University of Electronic Science and Technology of China, 2013.

[3]赵会茹, 杨璐, 李春杰, 等. 基于协整理论和误差修正模型的电网投资需求预测研究[J]. 电网技术,2011,35(9):193-198.

ZHAO Huiru, YANG Lu, LI Chunjie, et al. Research on prediction to investment demand of power grid based on co-integration theory and error correction model[J]. Power System Technology, 2011,35(9):193-198.

[4]周盈, 邹波, 文福拴, 等. 针对不同发展阶段的电力网络投资需求分析[J]. 电力系统及其自动化学报,2015,27(8):8-13.

ZHOU Ying, ZOU Bo, WEN Fushuan, et al. Investigation on power network investment demands at different development stages [J]. Proceedings of the CSU-EPSA, 2015, 27(8):8-13.

[5]郑琳. 电网建设项目投资优化管理方法与应用[J]. 电力建设,2011,32(1):104-107.

ZHENG Ling, Optimal management method and its application in grid project portfolio [J]. Electric Power Construction, 2011, 32(1): 104-107.

[6]崔巍, 都秀文, 杨海峰. 供电公司投资规模模型研究[J]. 电力建设,2013,34(8):27-33.

CUI Wei, DU Xiuwen, YANG Haifeng. Investmentscale modle of power supply company [J]. Electric Power Construction, 2013, 34(8): 27-33.

[7]张富强, 罗慧, 刘梅招,等. 基于基尼系数的电力网络投资分配模型及应用[J]. 电力建设, 2016,37(1):9-14.

ZHANG Fuqiang, LUO Hui, LIU Meizhao,et al. A Gini coefficient based investment allocation model for power networks and its application [J]. Electric Power Construction, 2016,37(1):9-14.

[8]韩柳, 彭冬, 王智冬, 等. 电网评估指标体系的构建及应用[J]. 电力建设,2010,31(11):28-33.

HAN Liu, PENG Dong, WANG Zhidong, et al. Constitution and application of the index system for power grid assessment [J]. Electric Power Construction, 2010,31(11):28-33.

[9]梁双,范明天,苏剑. 城市电网性能评价指标框架的研究[J]. 供用电,2009,26(5):8-11,15.

LIANG Shuang, FAN Mingting, SU Jian. Research on theevaluation index framework of urban power network[J]. Distribution & Utilization, 2009,26(5):8-11, 15.

[10]张龙, 曾鸣, 沈红宇,等. 不同电力体制改革背景下国际标杆电网评价体系研究及借鉴[J]. 电力建设,2015,36(11):148-153.

ZHANG Long, ZENG Ming, SHEN Hongyu, et al. International benchmarking grid assessment systems research and reference under different electricity system reform background[J]. Electric Power Construction, 2015,36(11):148-153.

[11]徐科, 刘明志, 张军,等. 世界一流城市电网评价指标体系[J]. 电力建设,2015,36(11):51-57.

XU Ke, LIU Mingzhi, ZHANG Jun, et al. Index system for world-class urban power network [J]. Electric Power Construction, 2015,36(11):51-57.

[12]万卫, 王淳, 程虹, 等. 电网评价指标体系的初步框架[J]. 电力系统保护与控制,2008,36(24):14-18.

WAN Wei, WANG Chun, CHENG Hong, et al. Preliminary frame of index system for evaluating power network [J]. Power System Protection and Control, 2008,36(24):14-18.

[13]李连结, 姚建刚, 龙立波, 等. 组合赋权法在电能质量模糊综合评价中的应用[J]. 电力系统自动化,2007,31(4):56-60.

LI Lianjie, YAO Jiangang, LONG Libo, et al. Application of combination weight method in fuzzy synthetic evaluation of power quality[ J].Automation of Electric Power Systems, 2007,31(4):56-60.

[14]胡列翔, 徐谦, 张全明,等. 电网发展的阶段论[J]. 浙江电力,2011(12):9-11,73.

HU Liexiang, XU Qian, ZHANG Quanming, et al. On stage of power grid development [J]. Zhejiang Electric Power, 2011(12):9-11, 73.

[15]徐志奇. 电网投资评价系统模型研究与应用[D].北京：华北电力大学,2012.

XU Zhiqi. Research andapplication of investment evaluation system model for power grid [D]. Beijing: North China Electric Power University,2012.

(编辑 刘文莹)

Investment Allocation Method Based on Performance Evaluation of Different Levels of Power Grid

GE Liang1, XU Qian2, CHENG Haozhong1, LAN Zhou2, LIU Lu1

(1. Key Laboratory of Control of Power Transmission and Conversion (Shanghai Jiao Tong University), Shanghai 200240, China; 2. State Grid Zhejiang Electric Power Corporation Economic Research Institute, Hangzhou 310008, China)

Considering the performance evaluation of different levels of power grid, this paper studies an investment allocation method. Firstly, we divide power grids into different levels according to their different characteristics, and establish the performance index systems of different levels of power grid. We applied comprehensive evaluation method based on fuzzy mathematics to evaluate the grid performance, and used the logistic curve to fit the relationship between grid performance and cumulative investment. Then, we established the investment allocation model with the minimum variance of the grid performance margin as the target. Finally, the power grid of a province in eastern China was conducted to make validation and analysis as an example, and the investment quota of different levels of power grid during the “13th Five-year plan” period was is given. The results are reasonable and credible, which proves the feasibility of the proposed investment allocation method.

investment allocation; performance evaluation; different levels of power grid; logistic

国家自然科学基金项目(51337005)；国网浙江省电力公司科技项目(5211JY150008)

TM 71

A

1000-7229(2016)12-0143-08

10.3969/j.issn.1000-7229.2016.12.019

2016-08-22

葛亮(1992)，男，通信作者，硕士研究生，主要研究方向为电网经济性规划；

徐谦(1963)，男，高级工程师，主要从事电网规划及新能源并网等方面的管理和技术工作；

程浩忠(1962)，男，教授，主要研究方向为电力系统规划、电力系统运行；

兰洲(1980)，男，高级工程师，主要从事输电网规划研究方面的工作；

柳璐(1983)，女，助理研究员，主要研究方向为输电网规划和评估。

Project supported by National Natural Science Foundation of China(51337005)