计及可入网电动汽车的微电网电源优化配置

叶晨晖，周玲，张木银，管志成

(河海大学能源与电气学院，南京市 211100)

计及可入网电动汽车的微电网电源优化配置

叶晨晖，周玲，张木银，管志成

(河海大学能源与电气学院，南京市 211100)

计及可入网电动汽车(plug-in electric vehicle，PEV)、微电网中多种分布式电源(distributed generation，DG)输出功率的不确定性，综合考虑了DG投资、运维等成本，以及微电网带来的节能、降损、减少用户停电损失收益等因素，进行微电网电源的优化配置。PEV接入微电网后，可以根据微电网的实际运行情况作为储能装置补充原有储能元件，从而减少储能元件容量，提高微电网的经济性。从PEV参与微电网运行调度出发，建立计及PEV的微电网电源优化配置模型。算例结果表明，该模型最优解可以确保投资的最佳经济性，获得较大社会经济收益，为含PEV的微电网电源优化配置提供理论依据。

可入网电动汽车(PEV)；收益成本比；电源优化配置；用户停电损失

0 引 言

随着世界各国能源机构的调整，可再生能源的开发是一个必然趋势。作为集成了多类型分布式电源(distributed generation，DG)、储能以及控制装置的单一可控网络系统[1]，微电网以其对可再生能源的有效利用及灵活、智能的控制特点，受到越来越多的关注。同时，随着节能减排政策的激励和能源开发技术的进步，可入网电动汽车(plug-in electric vehicle，PEV)在电力系统中的应用日益广泛。PEV接入微电网后，自身的储能装置增加了微电网的储能元件容量，PEV在充电时，本质上是从微电网吸收功率，增加了微电网总的负载，然而，当PEV充满电后，储能装置接入微电网，可以参与微电网的优化调度，即充当微电网储能元件，减少微电网原有的储能元件容量，从而节约微电网的投资成本。因此，有必要在对微电网电源的优化配置时，考虑PEV的影响，以适应未来电网的发展。

目前，国内外对微电源的优化配置已经做了一些研究工作。文献[2]在用户激励响应行为的基础上建立了计及需求侧响应的双层优化调度模型，但考虑DG的种类比较单一；文献[3]建立了较全面的多目标优化模型，在计算DG带来的收益时计及了环境等收益，但未考虑DG出力的随机性；文献[4-5]在孤岛运行状态下对微电源进行优化配置，研究了风能和太阳能的随机特性，但未考虑PEV接入的影响，优化结果不能完全适应未来电网的发展；文献[6-8]研究了DG和电动汽车充电站的选址定容问题，建立了以综合成本最小为目标的模型，但未考虑微电网投资的经济性。

本文从投资、运行成本和配置收益角度考虑，首先计算DG投资、燃料购买、运行和维护等成本，以及节能、减排、降损、减少用户停电损失的综合社会经济收益，建立基于年化收益成本比最大的含PEV微电网电源的优化配置模型，同时考虑PEV、储能元件的充放电功率、DG准入容量的约束，并运用改进细菌觅食算法对模型进行求解，得到不同情形下微电网电源的优化配置结果。

1 系统微电源模型

1.1 风机、光伏出力模型

微电网中含有大量的风力发电机，其输出功率随风速变化而变化。大部分地区的风速随机变化特性近似服从Weibull分布[9]。根据风速的概率密度函数可以得出风速v，从而计算出风力发电机的出力PWT。

光伏电池是微电网的重要部分，其输出功率与光照强度有关。光伏出力模型参考文献[10]。根据太阳光照下电流变化的温度系数、太阳辐射以及光伏电池温度参考值、光伏阵列倾斜面上的总太阳辐射、光电池温度，然后计算出光伏发电的输出功率Ppv。

1.2 PEV储能状态模型

电动汽车可以根据电池的充放电特性，在微电网负荷高峰时，将储存的电能释放到系统中，在用电低谷时，电池充当负荷从系统中吸收电能，从而达到削峰填谷的目的。PEV可以与风机和光伏等随机性较强的电源形成互补[11]，来提高系统的稳定性。

本文假定微电网中的电动汽车均可以参与调度，且均充满电后与微电网断开。经过1天用车后再次充电的初始荷电状态(state of charge，SOC)为

(1)

式中：Lmax为PEV在电池充满电时可行驶的最大路程；Ld为PEV在电池充满电的情况下1天行驶的实际路程，近似满足对数正态分布[12]。

(2)

式中σL和μL为分布参数。

电动汽车分为充电和放电2种工作状态，不同工作状态下，电动汽车电池的储能荷电状态CSOC,ev(t)不同。充电时满足：

(3)

放电时满足：

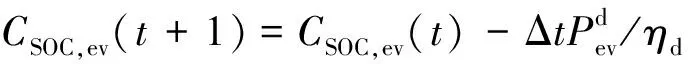
(4)

1.3 储能元件模型

为了简化分析，设定储能元件在整个充放电过程中，储能元件电池两端的电压基本维持不变。与电动汽车类似，储能元件的工作状态也分为充电和放电2种工作状态[13]。充电时，储能元件在t时段的储能荷电状态满足：

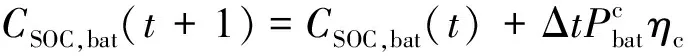
(5)

放电时满足：

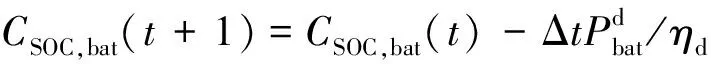
(6)

2 微电网电源的优化配置模型

2.1 目标函数

本文以微电网年化收益成本比最大为目标函数，同时考虑储能元件充放电功率、DG容量限制以及碳排放等约束对电源进行优化，目标函数为

(7)

式中：GTotal(s)、CTotal(s)分别为微电网电源优化配置的年化综合收益与成本；决策变量s=[s1,s2,…,si,…,sN]，si为第i种DG的台数。

2.2 年化综合收益

年化综合收益的计算公式为

GTotal(s)=GES(s)+GER(s)+GLR(s)+GRB(s)

(8)

式中：GES(s)为节能收益；GER(s)为减排收益；GLR(s)为降损收益；GRB(s)为提高可靠性收益。

(1)节能收益。微电网节能收益主要体现在利用可再生能源所节约的传统化石能源。

(9)

式中：lc为火电机组单位电能的平均煤耗量，本文取357 g/(kW·h)；pc为煤炭价格，本文取700元/t[14]；Ei为第i种DG的年发电量；EMT、sMT分别为微型燃气轮机的年发电量和安装台数；ε为供热比，即供热能量与发电供热总能量的比值；η1为热损效率，取0.2；lh、lco分别为溴冷机制热、制冷系数，均取1.2；ph、pco分别为热价和冷价，分别取51.4元/GJ和79.6元/GJ。

(2)减排收益。传统能源发电产生的污染气体主要是CO2，故采用微电网电源优化配置后相对燃煤发电等发电量CO2排放的减少量来表征减排效益。

(10)

式中：VCO2为CO2的环境价值；ηc、ηi分别为燃煤机组以及第i种DG生产单位电能所排放CO2的数量，文献[15]给出燃煤发电CO2的排放为822.80 g/(kW·h)，风机、光伏发电以及PEV的CO2排放量为0，CO2排放征收标准为9.75元/t。

(3)降损收益。对降损收益采用微电网电源优化配置后电能损耗减少的费用来进行量化。

(11)

(4)减少用户停电损失收益。微电网减少用户停电损失收益用配置前后减少的期望停电损失来衡量。

(12)

式中：fIEAR为停电损失评价率；λk、tk分别为微电网并网运行中负荷点k的平均停运率和时间；PM为微网孤岛失效率，取0.3；TR为电源重启时间；PL为平均负荷；PISO为微电网全年孤岛运行概率；ELSP,t(s)为微网孤岛运行状态下t时段的缺电量。

2.3 年化综合成本

本文综合考虑DG投资费用、运行维护成本以及燃料成本，计算微电网电源优化配置的年化综合成本。

CTotal=CorIcrf+Cm+Cfuel

(13)

式中：Cor、Cm、Cfuel分别为微电网初始投资成本、年运行与维护费用、年燃料成本；Icrf为资金回收系数，将现在值等年值化，其计算公式[9]为

(14)

式中：r为贴现率；N为系统生命周期。

Cor、Cm、Cfuel的计算公式如下详述。

(1)初始投资费用Cor。Cor包含微电网内各电源的投资和安装费用。

(15)

式中：Xi为第i种DG的装机容量；μi11、μi12分别表示第i种微电源的单位容量投资与安装成本。

(2)年运行与维护费用Cm。

(16)

式中：μi2为第i种微电源单位发电量的维护费用；Ei(n)为第i种微电源在第n年的年发电量；r为贴现率，在本文中取r=5%；系统生命周期年限N取20。

(3)年燃料成本Cfuel。

(17)

式中μi3为微电网中第i种电源单位发电量的燃料费用。

2.4 约束条件

(1)系统功率约束。

(18)

式中：Pi(t)、Qi(t)分别为各节点注入的有功功率和无功功率；Ui(t)、Uj(t)分别为节点i和节点j的电压幅值；Gij、Bij分别为支路ij的电导和电纳；θij(t)为节点i和节点j的相角差。

(2)储能元件约束。为了防止过度充电或过度放电对储能元件造成损害，其荷电状态需限制在最大、最小荷电状态之间。

CSOC,min≤CSOC,bat(t)≤CSOC,max

(19)

式中CSOC,min和CSOC,max分别为储能元件的最小荷电状态和最大荷电状态。

本文假设在充放电过程中，储能电池两端的电压基本不变，储能元件的充放电功率应满足：

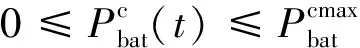
(20)

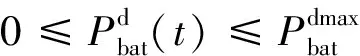
(21)

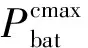
(3)电动汽车约束。SOC值是指电池在一定的放电倍率下，剩余电量与相同条件下额定容量的比值，充放电过程中电池的SOC值有一定限制。

CSOC,min1≤CSOC,ev(t)≤CSOC,max1

(22)

式中CSOC,min1和CSOC,max1分别为电动汽车电池的最小荷电状态和最大荷电状态。

同时，电动汽车充放电时，需要考虑单位时段充放电的最大功率和最小功率。

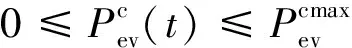
(23)

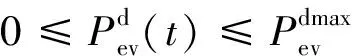
(24)

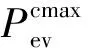
(4)DG准入容量约束：

(25)

式中SDGi和SDGmax分别为第i个DG的装机容量和微电网DG接入的总装机容量。

3 改进细菌觅食算法

细菌觅食算法(bacterial foraging algorithm，BFA)是2002年由Kevin M. Passino提出的仿生优化算法，基本细菌觅食算法的介绍可参考文献[16]。然而，在实际应用时，BFA仍然存在早熟等缺陷。结合本文的微电网电源优化问题，存在的待改进的问题为：(1)微电网电源的优化配置是一个非线性整数规划问题，本文中将每种DG的电源数量作为变量，而基本BFA算法变量是一个范围内的实数；(2)驱散过程中对个体细菌驱散行为使得接近最优的细菌被驱散，影响寻优速度；(3)繁殖时，对接近最优群体的复制未完全提升算法寻优的方向性。

针对以上几个问题，本文对基本BFA算法进行了改进。

(1)以第i种DG的台数si构成的矢量作为一个细菌，计算出的微电网电源等年值投资费用的解对应细菌的健康状态Jθ，即优化函数的适应值。

(2)驱散时，将适应度排序靠后的1/2个体驱散至随机位置，计算公式为

(26)

式中：Ci为第i个细菌向某一方向的移动向量；εi为单位向量；θr(j,k,l)为随机在第j次趋向，第k次繁殖，第l次驱散操作的个体位置。

(3)繁殖时，将存活的细菌分裂成Z1、Z22个种群，分别利用公式(27)—(28)进行趋向操作。

(27)

(28)

式中：θi(j,k,l)为第i个细菌位置；θm(j,k,l)为适应度最优的个体位置。

改进BFA算法的流程如图1所示。

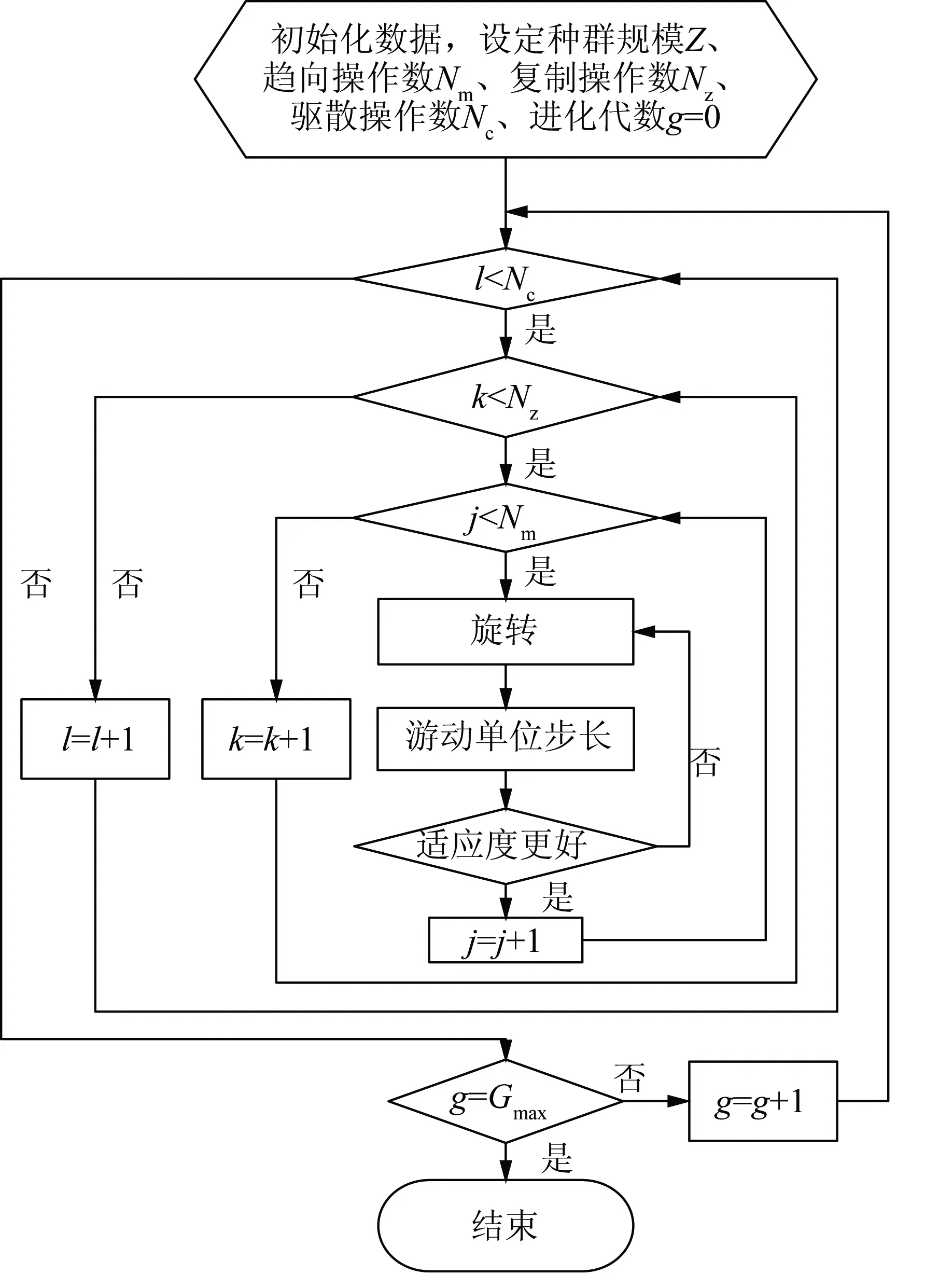
图1 改进BFA流程

4 算例分析

4.1 微电网的经济性分析

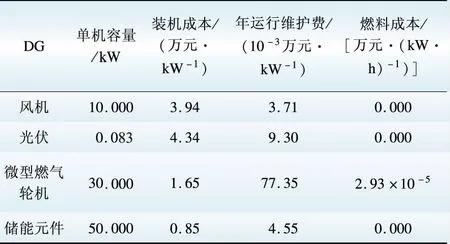
运用本文所建立的模型对微电网电源进行优化配置。结合文献[16]某实际微电网线路构造算例，验证本文所提模型的有效性。该地区微电网远景年负荷峰值为190.7 kW，平均负荷为104.3 kW，线路总长度为5 km，线路单位阻抗为(0.120+j 0.077)Ω/km，各机组的参数如表1所示，由实际数据生成风速和光照强度的概率模型。

表1 不同DG容量、成本参数

Table 1 Different capacities and cost parameters of DG

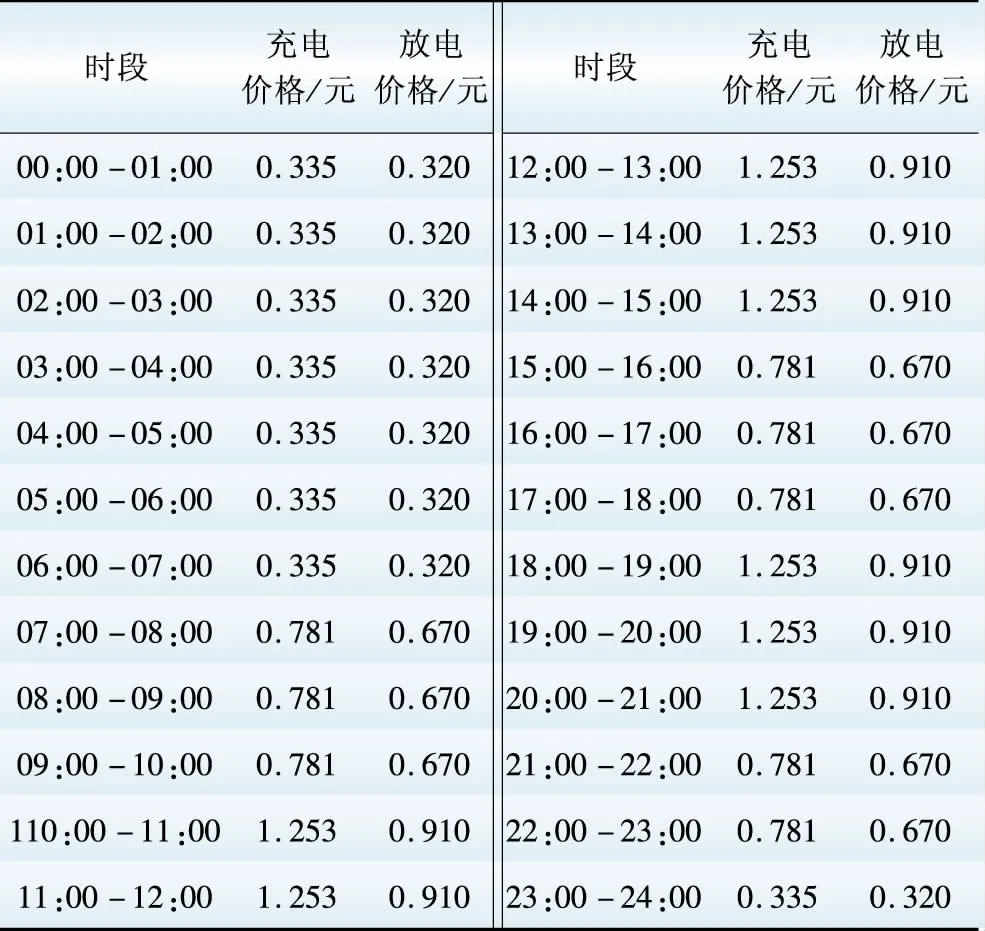
假设可调配的PEV数量为300辆。设置PEV的最大充电和放电功率为3.6 kW，常规电动汽车可在6 h内充放电完毕。其充放电价格如表2所示。以本文提出的年化收益成本比最大为目标，应用改进的细菌觅食算法分别对PEV不参与微电网调度以及PEV参与微电网调度进行微电网电源优化配置的求解。

表2 不同时段PEV的充放电价格

Table 2 Charging and discharging price of PEV at different period of time

4.1.1 PEV不参与调度

不考虑电动汽车的放电作用，只作为充电负荷。在分时定价引导机制下，以微电网年化收益成本比最大为目标函数，得出电动汽车的充电功率如图2所示。在时段09:00—16:00是电动汽车的充电高峰期，此时微电源的发电量比较充裕；在时段18:00—24:00电动汽车充电需求较少，此时微电源的出力不是很充裕。由于上午充电电价低，在时段01:00—07:00电动汽车充电比较集中。

图2 电动汽车充电功率

4.1.2 PEV参与微电网调度

电动汽车充分发挥其储能优势，在微电源出力充足时，将多余电能储存在电动汽车蓄电池中，在微电网用电高峰时段，再将电能释放到电网中，以达到削峰填谷的目的。在此情形下，电动汽车的充放电功率如图3所示。

图3 电动汽车充放电功率

在时段01:00—08:00，微电网中负荷需求不大，充电价格低，电动汽车充电较为集中；在时段 13:00—22:00，负荷逐渐增加，而微电网中的风机、光伏出力减少，此时为了维持微电网平衡，电动汽车开始减少其充电次数，转而向微电网释放电能以缓解用电压力。表3给出了以年化收益成本比最大为目标，2种情形下微电网电源最优配置的结果。图4计算了表3中各配置方案的4项社会经济收益。

表3 年化收益成本比最大目标下微电源优化方案结果

Table 3 Microgrid power optimization scheme results under the maximum annual profit cost target

图4 不同数量PEV接入情况下微电网的各项收益

对比表3中的数据可知：在PEV 2种运行情形下，微电网年化收益成本比均大于1，这表明微电网电源优化配置带来的社会经济收益远远高于其电源的配置成本。

考虑PEV的影响虽然增加了微电网的综合成本，但PEV与DG配合带来了较大的节能、减排等综合收益。尤其在节能方面，PEV参与微电网调度的作用显著，并且随着PEV入网后，风机和光伏的比重逐渐增加，储能元件的比重逐渐减小，微电网的年化收益成本比逐渐提高。这表明PEV参与调度使得微电网对可再生能源的接纳能力得到有效提升，同时减少了储能元件的容量。

4.2 算法比较

本文通过改进BFA计算结果与一般BFA和遗传算法(genetic algorithm，GA)比较，该微电网在情形1时配置成本与迭代次数的关系如图5所示。

图5 算法收敛特性曲线

对比3条曲线可知：本文采用的改进BFA收敛速度最快。当迭代次数为55时，改进的BFA算法已经取得全局最优解，微电网年化收益成本比稳定在1.60附近，而一般BFA以及GA算法分别在迭代次数为104和109时，达到全局最优解。改进BFA算法对算例运行50次，91%可收敛至全局最优解，而一般BFA与GA算法分别只有70%、74%可以收敛至全局最优解。显然，本文采用的算法对本文模型的求解具有更高的稳定性。

5 结 论

(1)可入网电动汽车与DG配合带来了较大的节能等综合收益，尤其在节能方面，PEV参与微电网调度的作用显著，研究微电网电源优化配置时，计及PEV的影响能更准确地反映未来电网的特点。

(2)相比较传统遗传算法以及一般细菌觅食算法，采用改进BFA求解优化模型，具有收敛速度快、稳定性高等特点。

在本文研究的基础上可更深入地研究含多类型DG、储能系统以及PEV的微电网电源优化配置问题，为未来电网的发展做更充分的理论基础准备。

[1]CHEN S X, GOOI H B, WANG M Q. Sizing of energy storage for microgrids[J]. IEEE Transactions on Smart Grid, 2012, 3(1): 142-151.

[2]赵树青，杨秀，张美霞. 计及需求侧响应的含风电电网优化调度模型[J].电器与能效管理技术，2015(23)：69-74.

ZHAO Shuqing， YANG Xiu， ZHANG Meixia. Optimal dispatching model for wind farms integrated grid considering demand response[J]. Electrical & Energy Management Technology，2015(23)：69-74.

[3]王金全，黄丽，杨毅. 基于多目标粒子群算法的微电网优化调度[J].电网与清洁能源，2014，30(1)：49-54.

WANG Jinquan，HUANG Li，YANG Yi. Optimal dispatch of microgrid based on mult-objective particle swarm optimization[J]. Power System and Clean Energy，2014，30(1)：49-54.

[4]卢洋，卢锦玲，石少通，等. 考虑随机特性的微电网电源优化配置[J].电力系统及其自动化学报，2013，25(3)：108-114.

LU Yang，LU Jinling，SHI Shaotong, et al. Optimal siting and sizing of distributed generation planning in microgrid by considering stochastic characteristic[J]. Proceedings of the CSU-EPSA，2013，25(3)：108-114.

[5]余志勇，万术来，明志勇，等. “风光水”互补微电网的运行优化[J].电力建设，2014，36(6)：50-55.

YU Zhiyong，WAN Shulai，MING Zhiyong, et al. Optimal operation of complementary microgrid with hybrid wind-solar-hydro power [J]. Electric Power Construction，2014，36(6)：50-55.

[6]谢应昭，卢继平. 含风储混合系统的多目标机组组合优化模型及求解[J].电力自动化设备，2015，35(3)：18-26.

XIE Yingzhao，LU Jiping. Multi-objective unit commitment optimization model including hybrid wind-storage system and its solution[J]. Electric Power Automation Equipment，2015，35(3)：18-26.

[7]吴宇，张彼德，袁国森，等. 计及电动汽车和风光资源不确定性的微电网优化配置[J].电测与仪表，2016，53(16)：39-44.

WU Yu，ZHANG Bide，YUAN Guosen, et al. Optimal configuration of micro-grid considering uncertainties of electric vehicles and PV/wind sources[J]. Electrical Measurement & Instrumentation，2016，53(16)：39-44.

[8]范彬，周力行，黄頔，等. 基于改进蝙蝠算法的配电网分布式电源规划[J].电力建设，2015，36(3)：123-128.

FAN Bin，ZHOU Lixing，HUANG Di, et al. Distributed generation planning for distribution network based on modified bat algorithm[J]. Electric Power Construction，2015，36(3)：123-128.

[9]EVANGELOPOULOS V A, GEORGILAKIS P S. Optimal distributed generation placement under uncertainties based on point estimate method embedded genetic algorithm[J]. IET Generation, Transmission & Distribution, 2014, 8(3): 389-400.

[10]陈国恩，宗鹏鹏，朱伟，等. 计及可再生能源与负荷互补特性的储能随机调度[J].电力建设，2015，36(6)：27-33.

CHEN Guoen, ZONG Pengpeng, ZHU Wei, et al. Stochastic dispatching of energy storage devices considering complementarity between renewable energy and load[J]. Electric Power Construction，2015，36(6)：27-33.

[11]GHAHDERIJANI M M, BARAKATI S M, TAVAKOLI S. Reliability evaluation of stand-alone hybrid microgrid using sequential Monte Carlo simulation[C]//2012 Second Iranian Conference on Renewable Energy and Distributed Generation. Iran：IEEE, 2012: 33-38.

[12]和敬涵，谢毓毓，叶豪东，等. 电动汽车充电模式对主动配电网的影响[J].电力建设，2015，36(1)：97-102.

HE Jinghan, XIE Yuyu, YIP Tony et al. Influence of electric vehicles charging modes on active network distribution[J]. Electric Power Construction，2015，36(1)：97-102.

[13]李丹丹，苏小林，阎晓霞，等. 储能优化配置关键问题分析[J].电力建设，2016，37(9)：70-78.

LI Dandan, SU Xiaolin, YAN Xiaoxia, et al. Principal problems of energy storage optimization allocation[J]. Electric Power Construction，2016，37(9)：70-78.

[14]李登峰，谢开贵，胡博，等. 基于净效益最大化的微电网电源优化配置[J].电力系统保护与控制，2013，41(20)：20-26.

LI Dengfeng, XIE Kaigui, HU Bo, et al. Optimal configuration of microgrid power supply based on maximizing net benefits[J]. Power System Protection and Control，2013，41(20)：20-26.

[15]梁惠施，程林，苏剑. 微网的成本效益分析[J].中国电机工程学报，2011，31(增刊1)：38-44.

LIANG Huishi, CHENG Lin, SU Jian. Cost benefit analysis for microgrid[J]. Proceedings of the CSEE，2011，31(Supplement 1)：38-44.

[16]马溪原，吴耀文，方华亮，等. 采用改进细菌觅食算法的风/光/储混合微电网电源优化配置[J].中国电机工程学报，2011，31(25)：17-25.

MA Xiyuan, WU Yaowen, FANG Hualiang, et al. Optimal sizing of hybrid solar-wind distributed generation in an islanded microgrid using improved bacterial foraging algorithm [J]. Proceedings of the CSEE，2011，31(25)：17-25.

(编辑 景贺峰)

Optimal Configuration of Microgrid Power Supply Considering Plug-in Electric Vehicles

YE Chenhui，ZHOU Ling，ZHANG Muyin，GUAN Zhicheng

(College of Energy and Electrical Engineering, Hohai University, Nanjing 211100, China)

With comprehensively considering plug-in electric vehicle (PEV), the output power uncertainty of various distributed generations (DGs) in microgrid, the DG investment and operation cost, and the benefits of energy saving, loss reduction and outage loss decrease brought by microgrid, this paper optimizes the configuration of microgrid power supply. After the PEV is connected to the microgrid, it can be used as the energy storage device to supplement the original energy storage element according to the actual operation of microgrid, which can reduce the capacity of the energy storage element and improve the economic performance of the microgrid. From the aspect of PEV participating in the operation of microgrid, this paper establishes the optimal configuration model of microgrid power supply based on PEV. The results show that the optimal solution of the model can ensure the best economy of investment and obtain a larger social economic benefit, which provides theoretical basis for the optimal configuration of microgrid power supply with PEV.

plug-in electric vehicle (PEV); income cost ratio; optimal configuration of power supply; user outage loss

TM 727

A

1000-7229(2016)12-0082-07

10.3969/j.issn.1000-7229.2016.12.011

2016-09-01

叶晨晖(1992)，男，硕士研究生，本文通信作者，主要研究方向为分布式发电、微网、配电网规划；

周玲(1964)，女，副教授，硕士生导师，主要研究方向为电力系统继电保护、电力系统控制、故障诊断；

张木银(1992)，男，硕士研究生，主要研究方向为分布式发电、微网、配电网规划；

管志成(1992)，男，硕士研究生，主要研究方向为分布式发电。