基于主动配电网运行特性的电压质量评估

宋梦琪，陶顺，陈鹏伟

(新能源电力系统国家重点实验室(华北电力大学)，北京市 102206)

基于主动配电网运行特性的电压质量评估

宋梦琪，陶顺，陈鹏伟

(新能源电力系统国家重点实验室(华北电力大学)，北京市 102206)

主动配电网(active distribution network，ADN)在元件故障时可以主动组网隔离故障，实现部分持续供电。基于这一主动运行特性，计及主动配电网的多运行状态，提出了主动配电网的电压质量评估方法。首先对元件的状态持续时间抽样得到系统的状态与持续时间序列，并对系统各运行状态进行拓扑辨识和导纳参数辨识；然后对分布式电源的出力和负荷采用拉丁超立方抽样，孤岛模式下计及功率平衡原则执行储能和负荷的协调控制，得到分布式电源、储能和负荷的功率；最后对各运行状态进行概率潮流计算，对电压幅值结果进行统计分析，并用提出的节点电压偏差风险和孤岛节点失电率指标进行电压质量评估。将所提方法应用到基于RBTS-Bus2的主动配电网测试系统中，验证了所提方法的有效性。

主动配电网(ADN)；概率潮流；电压质量评估

0 引 言

随着配电网中分布式电源接入量和电动汽车普及率的不断增大以及可控负荷的增加，传统配电网已逐渐从被动模式向主动模式转变[1-3]。主动配电网是通过使用灵活的网络拓扑结构来管理潮流，以便对局部的分布式能源进行主动控制和主动管理的配电系统，其中分布式能源的基本构成是分布式发电(distributed generation，DG)、分布式储能、可控负荷等[4]。主动配电网在紧急情况下通过合理配置解列点，可使得主动配电网的局部作为微网，而以非常态的方式孤岛运行[4-5]。基于这一主动运行特性，在主动配电网的局部孤岛运行时，网络的平衡节点由公共连接点(point of common coupling，PCC)变为储能或者DG节点，影响潮流和电压分布。文献[6]指出微网在孤岛模式下的电能质量表征与并网不同，应该有比并网时更加严格的电能质量指标，因此有必要开展对主动配电网下电压质量的计算分析和评估。

潮流计算是电力系统电压质量评估的基础[7]，为综合考虑电网中分布式电源的随机性及其他不确定因素，概率潮流计算方法将概率论引入潮流计算中，得到了广泛应用。目前的研究主要集中在考虑分布式电源影响的概率潮流改进计算以及在此基础上的电压质量评估上[8-12]。然而主动配电网的潮流计算和评估则报道不多，其中文献[13]考虑了含逆变器微源的功率传变特性，结合前推回代算法建立了微电网随机潮流的计算方法。文献[14]采用半不变量法对孤岛微电网进行随机潮流和分析。但现有文献都没有考虑主动配电网在元件发生随机故障时可以主动组网，维持供电的主动运行特性。

主动配电网在元件发生随机故障时，网内及其与主网可以主动组网形成并网部分和孤岛部分维持供电。基于这一主动运行特性，本文提出主动配电网的电压质量评估方法，综合考虑在这一主动运行特性下元件的随机故障带来的网络拓扑和结构的多样性以及源荷的随机性，对主动配电网进行概率潮流计算，统计和分析电压幅值结果，并进行电压质量评估。

1 基本流程设计

计及随机故障，每个元件分别有运行和故障2种状态，所有元件状态的组合构成了主动配电网的多种运行状态。由于主动配电网具有发生故障后组网维持供电的主动运行特性，不同运行状态下的网络结构和微源(包括DG和储能)配置情况有显著差异。微源的故障与否决定了可运行DG的接入节点和数量；线路故障与否以及故障的位置和数量则决定是否有孤岛运行的情况发生并影响孤岛集合的数目以及并网和孤岛集合的拓扑。因此，运行状态对主动配电网的电压分布有较大的影响，为准确地评估主动配电网的电压质量，必须进行运行状态模拟。为模拟系统运行，本文首先对主动配电网进行时序状态模拟，获得系统状态与持续时间的序列；然后进行状态统计，对不同的运行状态分别进行网络运行状态辨识(拓扑辨识和导纳参数辨识)，并采用拉丁超立方抽样进行源荷随机变量模拟；继而进行潮流分析和评估。本文的电压质量评估基本流程设计如图1所示。图1中N为抽样次数，大小视收敛精度而定。

2 主动配电网的时序状态模拟与运行状态辨识

2.1 时序状态模拟

本文采用状态持续时间抽样法，基于对元件状态持续时间的概率分布抽样获得网络各元件的时序状态及持续时间，进而构成系统的状态与持续时间序列。

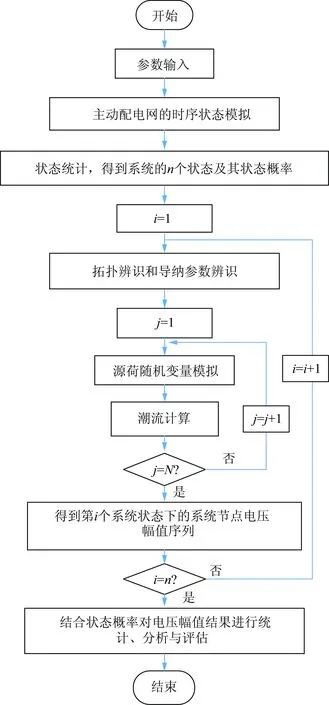
图1 主动配电网电压质量评估基本流程

元件采用两状态模型，0表示故障，1表示运行。假设所有元件初始时刻处于运行状态，对各元件形成1、0交替出现的状态序列，然后根据元件的故障率和修复率抽样获得满足指数分布的无故障工作时间和故障修复时间，从而模拟出时序下各元件的运行状态序列，如图2所示。

图2中：纵坐标表示元件状态，元件包括微源和配网内线路，共有l个，其中，将上级配电网视为电源，将其故障也考虑其中，断路器等开关设备的误动、拒动则等值考虑到线路故障率参数中；横坐标为时间轴，d1，d2，…，dn表示状态持续时间，T1，T2，…，Tn表示

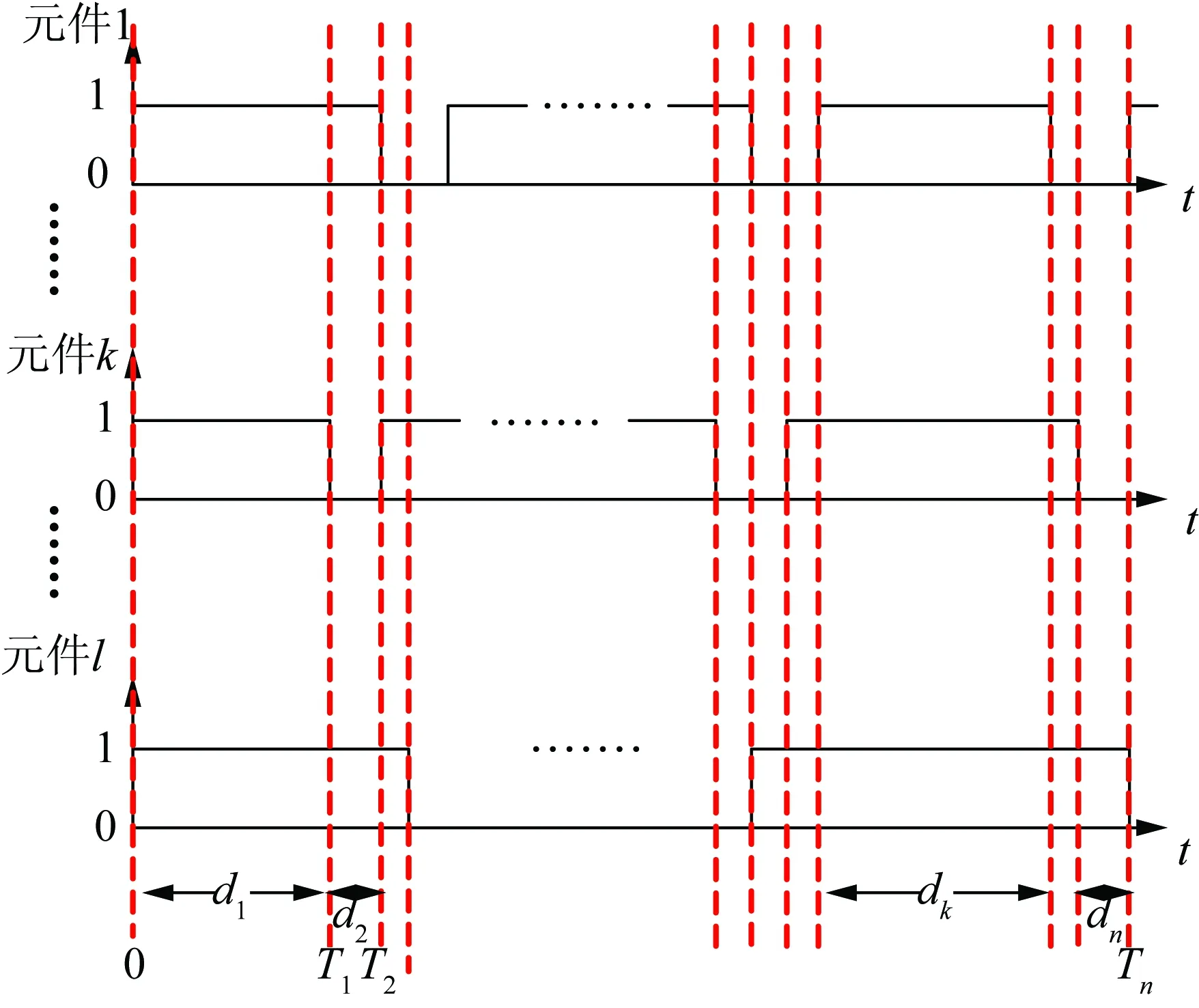
图2 时序状态模拟的过程

状态结束的时间，基准单位为h。综合所有元件在时序上的状态组合，即得到式(1)所示的系统状态，即持续时间序列S。

(1)

式中Sk为从Tk-dk+1到Tk时间内的各元件状态组合，为l行的列向量。

对S进行状态统计，即得到系统的各运行状态及状态概率。

2.2 拓扑辨识

针对每一个网络运行状态进行拓扑辨识，获得并网节点集合和孤岛节点集合，流程如下详述。

(1)连通域的判定。根据线路元件状态更新系统的邻接矩阵，基于广度优先搜索算法(breadth-first-search，BFS)[15]，对系统节点集合进行遍历，形成若干连通域，流程如图3所示。

(2)形成并网节点集合。筛选出含有PCC点的连通域，即为并网节点集合。

(3)形成孤岛节点集合。孤岛工况下，孤岛负荷节点由微源保证供电连续性，孤岛节点子集需要包含孤岛负荷节点及与之相连的微源。筛选出既含有负荷节点又含有无故障的“源”节点的连通域即为孤岛节点子集。各孤岛节点子集构成孤岛节点集合。

2.3 导纳参数辨识

系统网络模型可用网络元件参数和网络元件的连结关系确定，节点导纳矩阵包含这2个方面的信息，可以简单准确地描述网络模型，进行潮流计算。在对运行状态进行拓扑辨识之后，首先根据系统运行

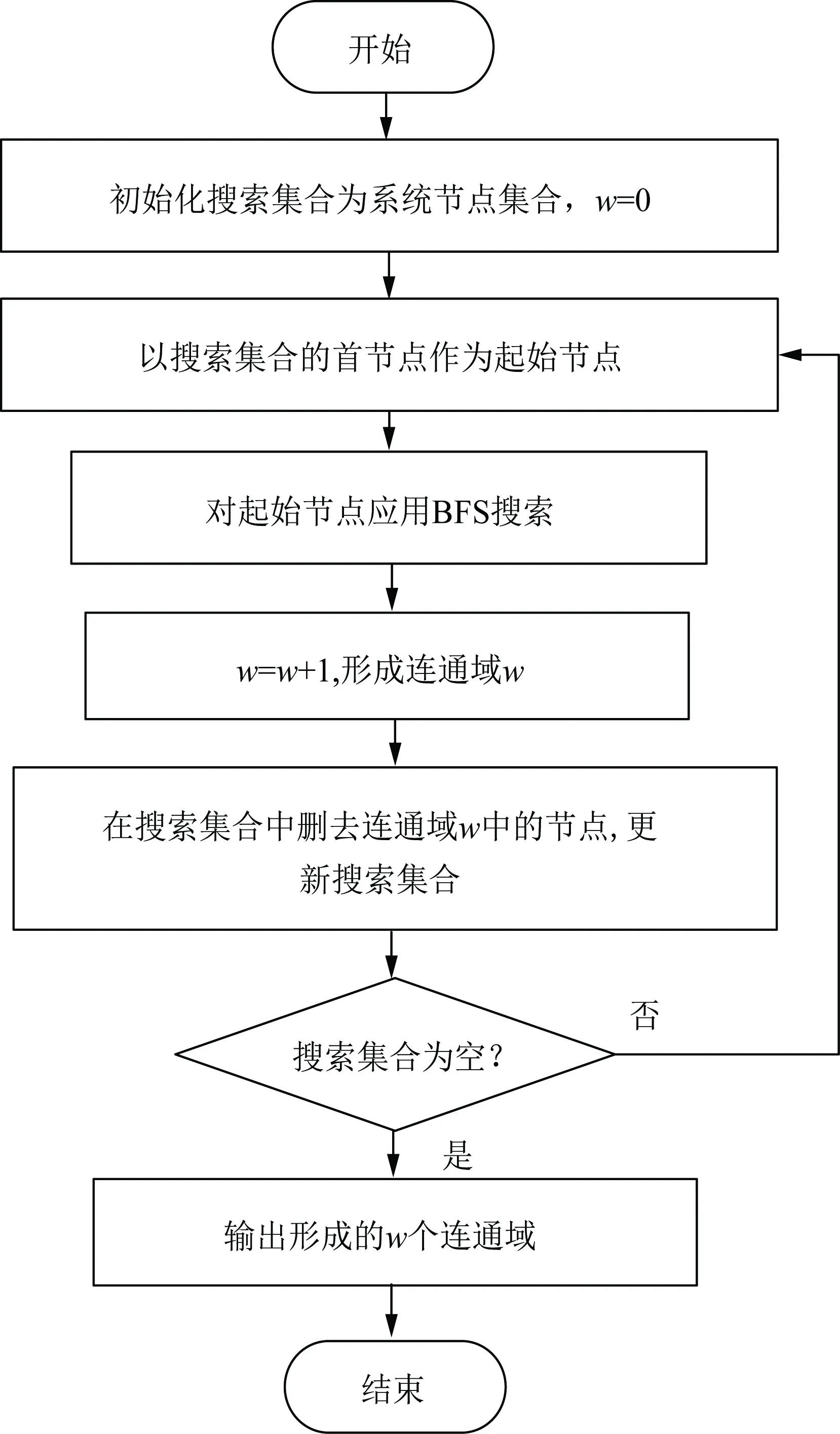
图3 连通域判定流程

状态借由以元件状态为权值的邻接矩阵更新系统的节点导纳矩阵的连接关系信息，形成状态更新后的系统节点导纳矩阵，然后对并网节点集合和孤岛节点子集分别对应节点提取互导纳信息，进而分别形成并网节点集合和孤岛节点子集的节点导纳矩阵。

3 源荷随机变量模拟与潮流计算

3.1 源荷随机变量模拟

对于风机、光伏和负荷的随机概率模型已有很多文献介绍，可视实际情况选取。在随机变量的概率模型建立后，本文对源荷的功率抽样采用拉丁超立方抽样法。该方法使抽样点的分布比较均匀，从而能够快速收敛。设随机变量抽样N次，拉丁超立方抽样将其累计分布函数的纵轴分成N个等间距，每个等区间的宽度为1/N，在每个区间均匀分布抽取一个随机数作为抽样值[8]。

设各变量相互独立，则对于随机变量Y，若Y的累积分布函数为F，第i次抽样值为yi，将1—N的整数随机打乱后得到的数字序列设为u，ui为u的第i个值，vi为0～1的随机数，则拉丁超立方抽样的结果为

(2)

孤岛运行时，视不同的运行目标可选用不同的运行原则对源荷功率进行修正。本文考虑当前微源可使用容量，尽可能地保证负荷供电可靠性，采用孤岛模式下的功率平衡原则，应用文献[16]的储能-负荷协调控制模型，由多储能装置间的充放电功率分配与功率缺额下的负荷协调优化控制来保证孤岛模式下的功率平衡，从而确定储能以及执行负荷控制后的负荷功率。考虑到储能装置优化运行以延长使用寿命的目标，负荷控制以优先供电-损失最小为原则，负荷控制与储能之间存在协调配合与优先级问题，储能装置与负荷的统一协调控制目标函数如式(3)所示。

(3)

式中：C为孤岛运行网络中储能装置可有效利用数；αi为储能装置i充放电引起的寿命损失成本系数，决定储能装置间充放电功率分配；PSB-i(t)为t时段对储能装置i的分配功率，PSB-i(t)>0为放电状态，反之为充电状态；D为孤岛运行网络中负荷节点数；βj为负荷节点j负荷控制损失系数，βj值的选择直接影响各负荷控制优先顺序，关键负荷的负荷控制损失系数远大于非关键负荷；xj为负荷控制决策变量；

PLC-j(t)为t时段对负荷节点j的可中断负荷。

约束条件考虑了孤岛运行功率平衡约束、储能装置在实际运行时存在的最大充放电功率约束和负荷节点的可控制性约束，具体见附录A。

3.2 潮流计算

在拉丁超立方抽样获得源荷的模拟功率后，基于第2节得到的网络拓扑和参数，采用前推回代法进行潮流计算，多次模拟即可得到各状态下的概率潮流结果。

主动配电网多运行状态下的潮流计算的关键在于平衡节点的确定。在并网运行时，PCC点为平衡节点，为配网系统提供电压支撑；当孤岛运行时，为使孤岛电网稳定运行，一般需要稳定的电压源支撑，储能电池是首选方案[17]，而当储能发生故障或者功率输出为0时，DG的逆变器控制可以起到维持电压的作用[18]，而对于没有被选作平衡节点的DG，均可简化处理为PQ节点[8]。

对辨识后的网络进行潮流计算的流程如图4所示。

4 统计分析与评估

4.1 统计分析

得到各状态下的概率潮流结果后，结合各状态的发生概率，应用条件概率公式可得到各电压偏差结果及其概率值，并基于此进行统计和分析。

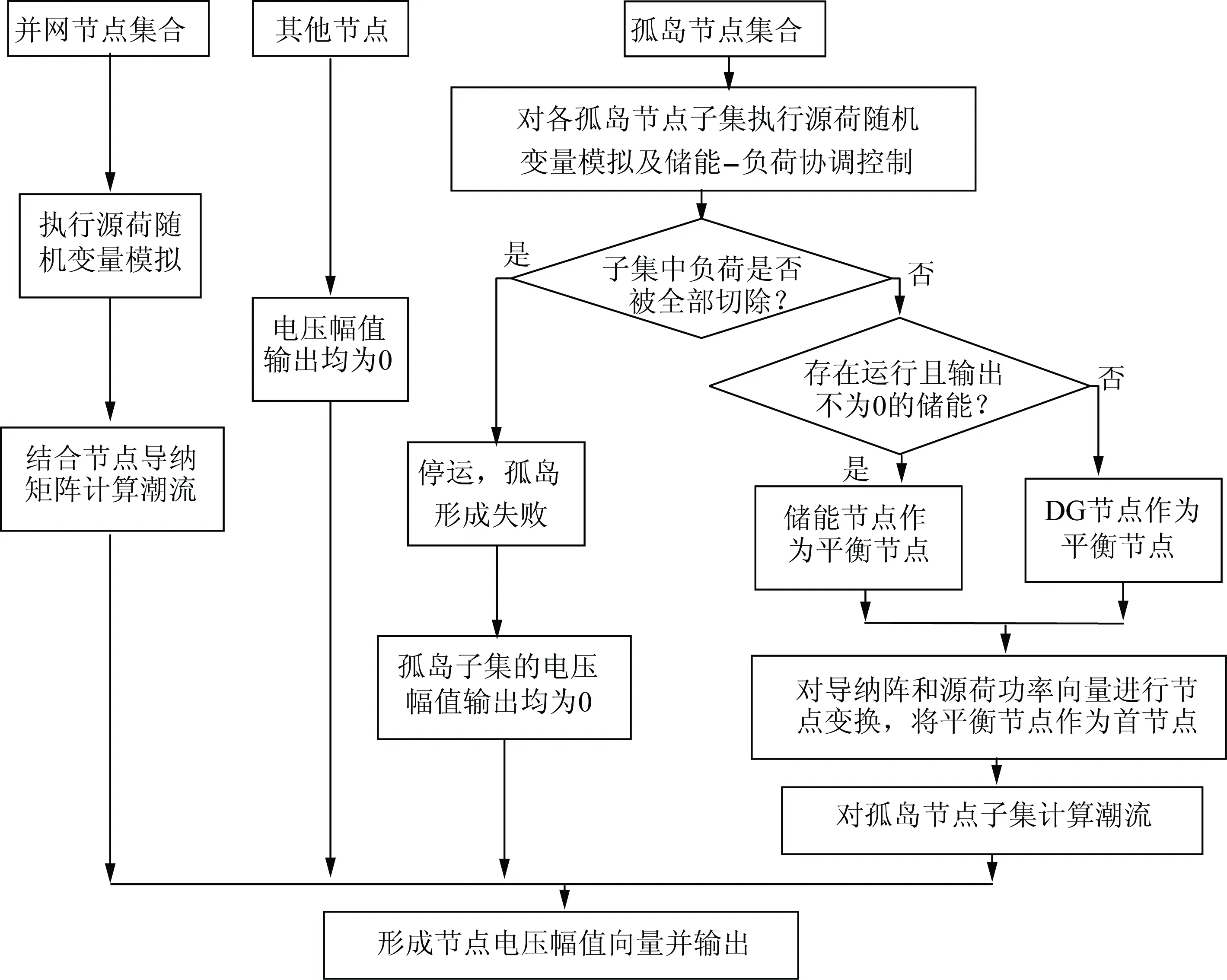
图4 潮流计算流程

4.2 评估指标

应用该计算方法进一步评估主动配电网中某些因素对并网和孤岛电压质量表征的影响。在评估过程中为方便定量比较，定义以下2个指标。

(1)电压偏差风险值。为综合考虑电压偏差的发生概率和严重程度，定量地反映主动配电网节点电压的偏差情况，本文将风险理论应用于主动配电网的电压质量评估中，定义节点电压偏差风险值SRISK为

(4)

式中：O为包含a个状态的系统运行状态集合；Oi为其中第i个状态；b为节点在Oi状态下模拟运行的非中断的电压幅值个数；Uij为节点在Oi状态下的第j个非中断电压幅值；p(Uij)为Uij在状态Oi中发生的概率；p(Oi/O)状态Oi在状态集合O中出现的概率。

(2)孤岛节点失电率。定义孤岛节点失电率Poutage为节点处于孤岛时电压中断的概率，反映主动配电网节点的持续供电质量。

(5)

式中：I为节点属于孤岛节点子集时的系统运行状态集合；Ii为其中第i个状态；p(Uoutage,i)为节点在状态Ii中电压为0的概率；p(Ii/I)为状态Ii在运行状态集合I中出现的概率。

5 算例分析

5.1 测试系统参数

本文在 RBTS Bus2系统[15]中截选F2与F4馈线并配置储能和DG，将修改后的系统作为电压质量评估测试系统，具体结构如图5所示。

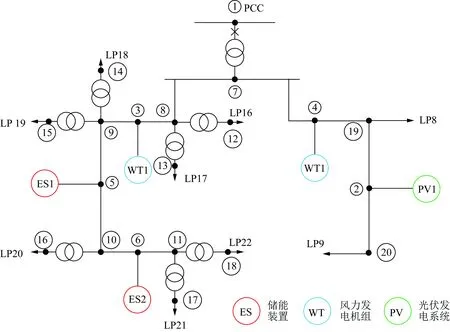
图5 电压质量评估测试系统

系统中PCC点处的变压器为35 kV /11 kV，容量为12.5 MV·A，其他变压器为11 kV /0.4 kV，容量为1 MV·A。各线路长度以及线路等网络元件故障率和修复时间参见文献[15]，各电源故障率和修复时间参考文献[19-20]，如表1所示。

算例计算收敛精度设为10-4。算例中光伏采用文献[21]中光伏发电系统的基本出力模型，风电机组出力随机模型参考文献[8]，负荷采用计及负荷类型的负荷随机模型，具体见附录B。各随机变量模型的参数取值如下详述。

表1 故障率和平均修复时间参数

Table 1 Parameter of failure rate and

mean time to resolution

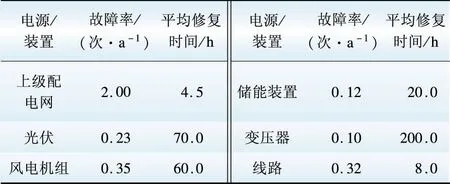
(1)光伏参数：标准测试条件下的太阳辐射强度为1 000 W·m-2；功率温度系数为-0.45%/℃；太阳电池组件的实际温度由正态分布抽样得到；标准测试条件下的电池温度为25 ℃；光照强度取自北京市某地某典型日数据。

(2)风机参数：切入风速为3 m/s；切出风速为 25 m/s；额定风速为12 m/s；尺度参数为8.53；形状参数为2。

(3)储能负荷协调控制参数参见文献[16]。

(4)负荷参数：由于本文选取的储能-负荷协调控制模型中负荷控制的优先顺序与负荷的重要程度有关，本文考虑了4类负荷，分别为商业负荷(节点12、18)、大用户(节点19、20)、居民负荷(节点13、14、15)、政府及医疗负荷(节点16、17)，4类负荷的日基本负荷水平序列如图6所示。

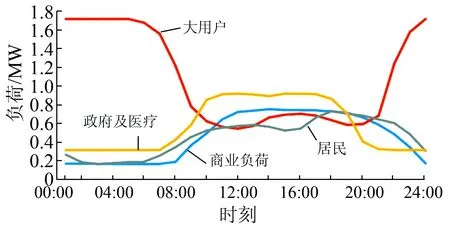
图6 4类负荷的负荷曲线

5.2 算例分析

应用本文方法对图5所示的测试系统在不同的DG渗透率下进行电压质量计算、分析和评估。由于当主动配电网存在孤岛运行时，孤岛网络的平衡节点从PCC点变成了储能或者DG节点，而并网和孤岛的平衡节点电压并不相同。为方便比较，本文用标幺值进行计算，平衡点电压为1 pu，得到的电压幅值可直观反映节点在并网和孤岛下节点电压相对各自平衡节点的偏差程度。

5.2.1 节点电压偏差概率统计与分析

DG渗透率固定，微源的配置为：2台1 MW风力发电机、1个0.8 MW光伏发电系统和2套 0.36 MW·h储能装置。其中储能装置最大充放电功率为 0.12 MW，各节点总平均负荷功率为5.539 9 MW，DG容量占负荷比例为50.54%。

由于并网状态的概率较孤岛状态大的多，计及对孤岛电压偏差概率分布的展现，分别统计同一负荷节点在并网和孤岛下的结果得到其电压幅值概率分布。以负荷节点17为例，其处于并网和孤岛时的电压幅值概率分布对比如图7所示。本算例中，孤岛的电压幅值概率分布是剔除了中断后的统计结果。

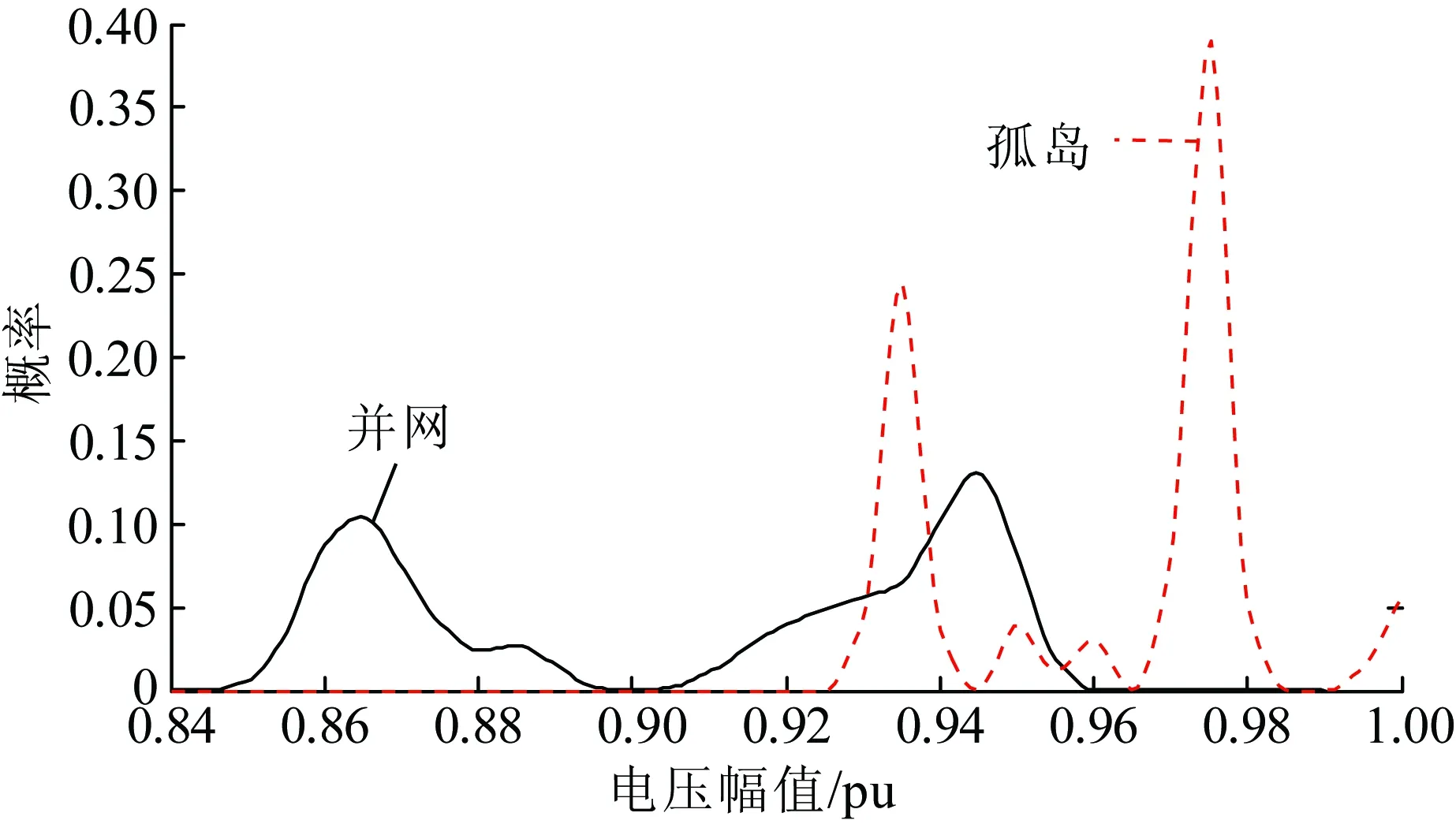
图7 节点17的电压幅值概率分布

图7中，节点17在并网时的电压分布呈现2个峰状分布。这是由于节点处于并网时系统无故障的状态概率远大于其他状态，而该状态下，在中午和下午日照强度达到顶峰的时段，光伏的出力及基本负荷水平在这一时段内变化都相对较小，电压幅值会在某一值附近集中，形成峰，由于此时处于重载时段，因此峰的位置在电压幅值较低处。而在夜间，光伏出力为0，加之基本负荷水平变化较小，电压形成第2个集中区域，由于处于轻载时段，为图中第2个峰。可见，两峰状分布形成的原因主要是由于功率的大幅波动(光伏)以及负荷水平的峰谷差。

类似地，每一个孤岛状态也倾向于形成两峰分布。但由于除了整个网络与上级配电网络脱离的情况，其他的孤岛状态网络都比并网时要小，且50%的渗透率往往不足以支撑整个孤岛网络的供电，一部分负荷会被切除，因此，每个孤岛状态下两峰的电压幅值普遍比并网时高，各孤岛状态下的两峰对应电压幅值分布也较为集中，对所有的孤岛状态统计得到孤岛电压分布呈现图7的趋势。从图7中可以看出，曲线在电压幅值为1 pu的位置呈现一个小的峰值，这是由于当该负荷节点被切除时，若支撑点到该节点之间没有运行的负荷或者微源，则会出现节点电压为1 pu的情况。

由图7还可以看出，节点处于孤岛时的电压幅值水平较并网时要高，分布更为集中，且相较于节点处于并网时系统无故障状态占主导地位呈现两峰趋势，节点17处于孤岛网络时呈现多峰趋势。

5.2.2 评估分析

应用该计算方法，本算例选取节点位置及DG渗透率2个影响因素评估其对电压质量的影响。

5.2.2.1 节点位置对电压质量的影响评估

在DG渗透率固定的情况下，分析比较与PCC点相距由远到近的3个节点的电压分布情况，其中节点17的电压分布见图7，节点15和节点12的电压分布如图8—9所示。

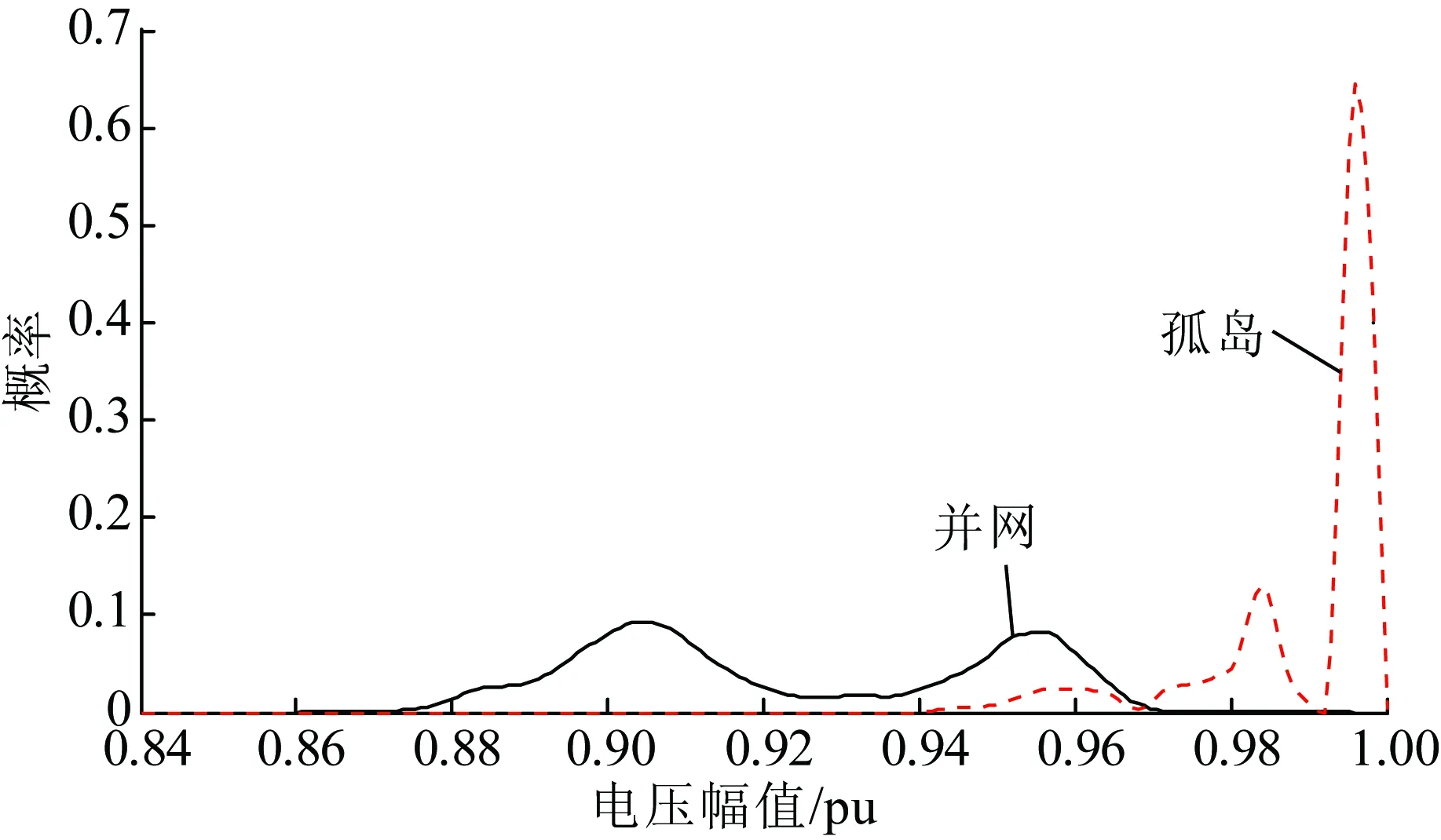
图8 节点15的电压幅值概率分布

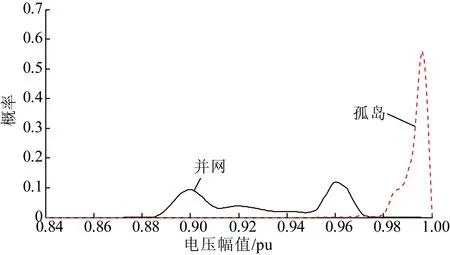
图9 节点12的电压幅值概率分布

由图7—9可见，这3个节点处于并网状态时，电压幅值分布都呈现2个高峰，且电压水平大小关系为节点12>节点15>节点17，即同一馈线上的负荷节点距离PCC点越近，其电压水平越高。

在孤岛状态下，电压幅值水平为节点12>节点15>节点17；集中度为节点12>节点15>节点17。这是由于相对于节点17仅靠近储能节点6，节点15距离其他微源都较节点17更近，而以节点12为中心，均匀分布了微源节点2、3、4、5，由于孤岛时的平衡节点具有随机性，因此，微源以其为中心均匀分布的负荷节点近平衡点的概率更大，孤岛电压幅值会更集中，呈现的峰数会更少，电压水平也会更高。

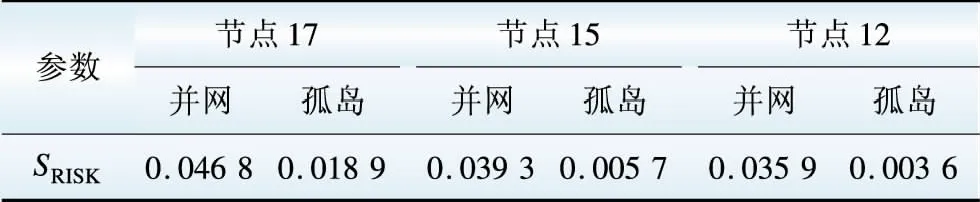
3个节点的电压偏差风险值如表2所示。由表2可得：并网时，同一馈线上的负荷节点距离PCC点越近，风险值越小；孤岛时，微源以其为中心均匀分布的负荷节点(节点12)的风险值最小，而微源距离节点成辐射分布的节点17的风险值最大。

表2 电压偏差风险值比较

Table 2 Comparison of voltage deviation risk values

5.2.2.2 DG渗透率对电压质量的影响评估

以节点17为例，对渗透率为30%和70%的结果也分别进行了计算、分析与评估，比较渗透率对并网和孤岛下电压分布的影响。

微源的配置为：(1)渗透率为30%的微源包含2台0.6 MW风力发电机、1个0.4 MW光伏发电系统和2套0.3 MW·h储能装置，其中储能装置最大充放电功率为0.15 MW，各节点总平均负荷功率为5.539 9 MW，DG容量占负荷比例为28.89%；(2)渗透率为70%的微源包含2台1.4 MW风力发电机、1个1.1 MW光伏发电系统和2套0.8 MW·h储能装置，其中储能装置最大充放电功率为0.4 MW，各节点总平均负荷功率为5.539 9 MW，DG容量占负荷比例为70.40%。

节点17在DG渗透率为30%和70%下的电压分布结果分别如图10—11所示。

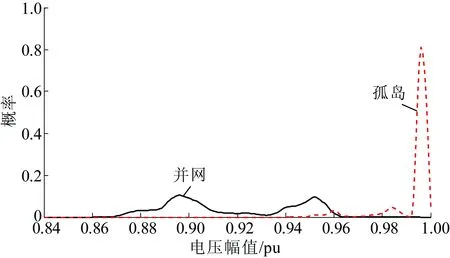
图10 30%渗透率下的节点17电压幅值概率分布

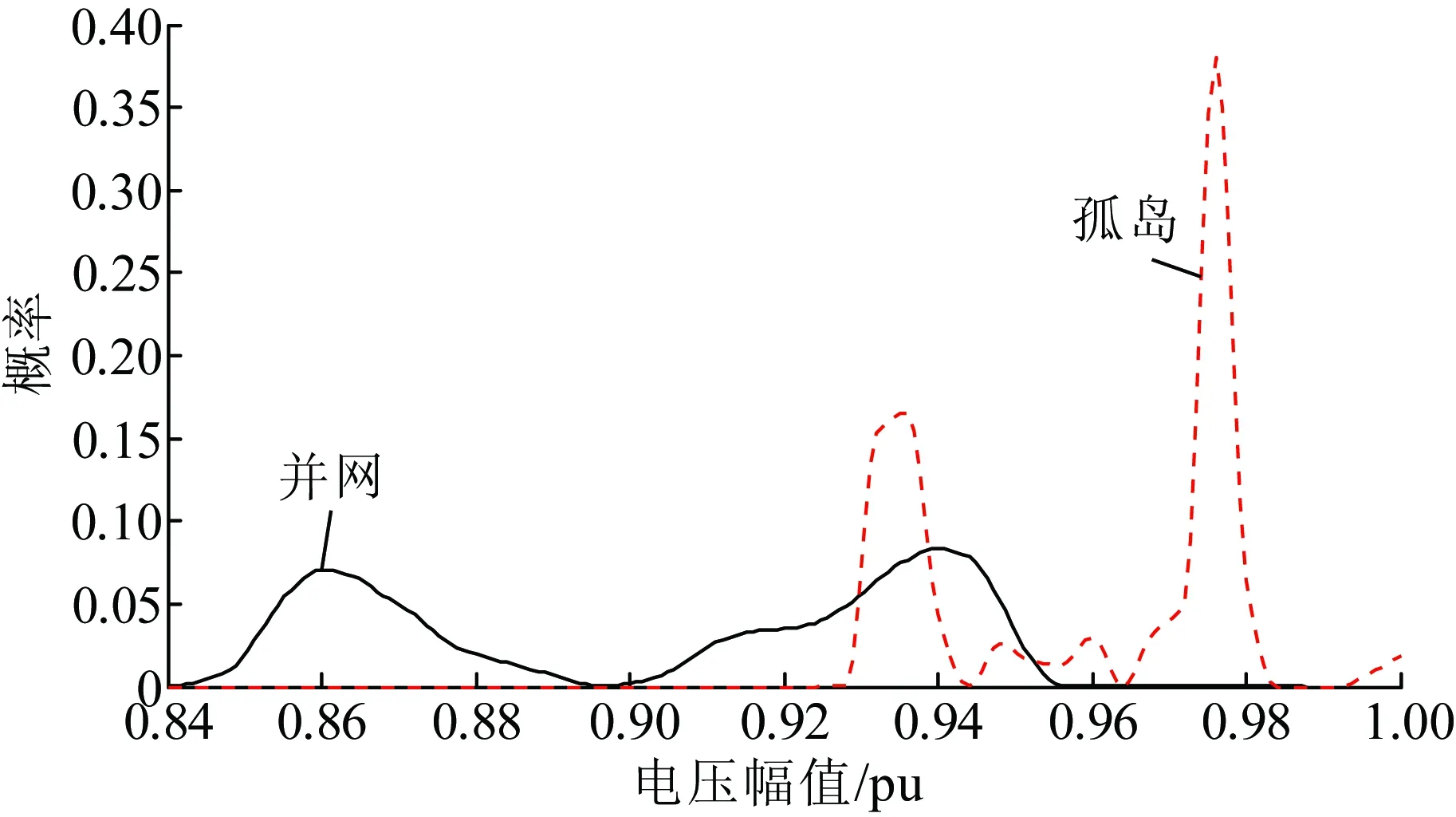
图11 70%渗透率下的节点17电压幅值概率分布

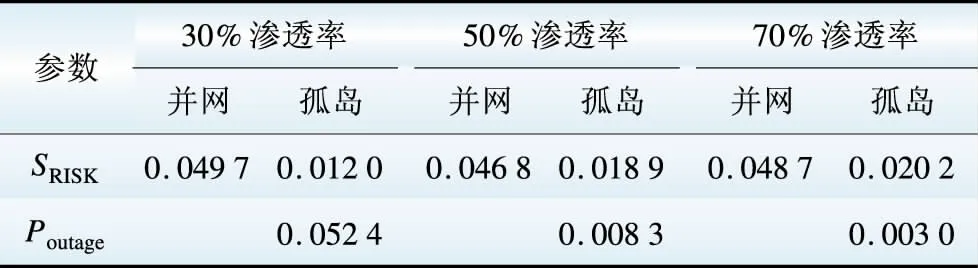
电压质量指标对比如表3所示。对比图10、图11和表3可知，节点17处于并网时，不同渗透率下的电压分布呈现相同的趋势，但渗透率越高，第1个峰值的对应电压幅值越小，曲线呈现沿横轴向左拉伸的趋势，这是因为渗透率越高，电压幅值受微源的状态和波动的影响越大。而处于孤岛时，渗透率越低，节点17的电压水平越高，并且越集中，风险值也越小，这是因为渗透率低的情况下，由于供求不平衡，更多的负荷被切除，网损大大减小，这就使得依然被供应的负荷节点的电压幅值较高。从孤岛节点失电率则可以看出，渗透率越低，孤岛节点失电率越高，可见，虽然此时电压质量集中度最高，偏差水平最小，但是持续供电质量较差。

表3 电压质量指标对比

Table 3 Comparison of voltage quality indices

6 结 论

(1)本文提出了基于主动配电网运行特性的电压质量评估方法，该方法可通过灵活设置不同的DG和负荷的模型以及孤岛时的运行原则来模拟主动配电网实际需要。本文选取源荷模型，采用能量平衡的孤岛运行原则，将此方法应用于测试系统，验证了方法的可行性和有效性。

(2)综合考虑负荷节点位置、DG渗透率对节点的电压偏差情况进行评估，可为主动配电网运行调压和规划提供参考。另外，在孤岛运行过程中结合节点电压偏差风险和孤岛节点失电率来开展主动配电网的电能质量评估，可综合考虑负荷的节点电压偏差和供电持续性。

本文计及主动配电网的孤岛运行能力这一主动运行特性，提供了一个主动配电网电压质量计算分析和评估的平台，进一步的工作可以考虑其他更加复杂的主动运行特点或规则，在本文所提出的平台基础上，修改主动运行规则，实现相应主动配电网的电压质量评估。

[1]赵波，王财胜，周金辉，等. 主动配电网现状与未来发展[J]. 电力系统自动化，2014，38(18)：125-135.

ZHAO Bo，WANG Caisheng，ZHOU Jinhui，et al. Present and future development trend of active distribution network[J]. Automation of Electric Power Systems，2014，38(18)：125-135.

[2]程林，刘琛，康重庆，等. 主动配电网关键技术分析与展望[J]. 电力建设，2015，36(1)：26-32.

CHENG Lin，LIU Chen，KANG Chongqing，et al. Analysis of development of key technologies in active distribution network[J]. Electric Power Construction，2015，36(1)：26-32.

[3]王成山，孙充勃，李鹏. 主动配电网优化技术研究现状及展望[J]. 电力建设，2015，36(1)：8-15.

WANG Chengshan，SUN Chongbo，LI Peng. Review and perspective on the optimization of active distribution network[J]. Electric Power Construction，2015，36(1)：8-15.

[4]范明天，张祖平，苏傲雪，等. 主动配电系统可行技术的研究[J]. 中国电机工程学报，2013，33(22)：12-18.

FAN Mingtian，ZHANG Zuping，SU Aoxue，et al. Enabling technologies for active distribution systems[J]. Proceedings of the CSEE，2013，33(22)：12-18.

[5]LASSETER R H. Smart distribution: coupled microgrids[J]. Proceedings of the IEEE, 2011, 99(6): 1074-1082.

[6]BOLLEN M, ZHONG J, LIN Y. Performance indices and objectives for microgrids[C]//Electricity Distribution-Part 1, 2009. CIRED 2009. 20th International Conference and Exhibition on. IET, 2009: 1-4.

[7]朱星阳，刘文霞，张建华，等．电力系统随机潮流及其安全评估应用研究综述[J]．电工技术学报，2013，28(10)：257-270．

ZHU Xingyang，LIU Wenxia，ZHANG Jianhua，et al. Reviews on power system stochastic load flow and its applications in safety evaluation[J]. Transactions of China Electrotechnical Society，2013，28(10)：257-270．

[8]张喆，李庚银，魏军强. 考虑分布式电源随机特性的配电网电压质量概率评估[J]. 中国电机工程学报，2013，33(13)：150-156.

ZHANG Zhe，LI Gengyin，WEI Junqiang. Probabilistic evaluation of voltage quality in distribution networks considering the stochastic characteristic of distributed generators[J]. Proceedings of the CSEE，2013，33(13)：150-156.

[9]余昆，曹一家，陈星莺，等. 含分布式电源的地区电网动态概率潮流计算[J]. 中国电机工程学报，2011，31(1)：20-25.

YU Kun，CAO Yijia，CHEN Xingying，et al. Dynamic probability power flow of district grid containing distributed generation[J]. Proceedings of the CSEE，2011，31(1)：20-25.

[10]彭寒梅，曹一家，黄小庆，等. 基于组合抽样的含分布式电源随机潮流计算[J]. 电力自动化设备，2014，34(5)：28-34.

PENG Hanmei，CAO Yijia，HUANG Xiaoqing，et al. Probabilistic load flow calculation based on combination sampling for power system containing distributed generations[J]. Electric Power Automation Equipment，2014，34(5)：28-34.

[11]丁明，王京景，李生虎. 基于扩展拉丁超立方采样的电力系统概率潮流计算[J]. 中国电机工程学报，2013，33(4)：163-170.

DING Ming，WANG Jingjing，LI Shenghu. Probabilistic load flow evaluation with extended latin hypercube sampling[J]. Proceedings of the CSEE，2013，33(4)：163-170.

[12]熊强，陈维荣，张雪霞，等. 考虑多风电场相关性的场景概率潮流计算[J]. 电网技术，2015，39(8)：2154-2159.

XIONG Qiang，CHEN Weirong，ZHANG Xuexia，et al. Scenario probabilistic load flow calculation considering wind farms correlation[J]. Power System Technology，2015，39(8)：2154-2159.

[13]段玉兵，龚宇雷，谭兴国，等. 基于蒙特卡罗模拟的微电网随机潮流计算方法[J]. 电工技术学报，2011，26(S1)：274-278.

DUAN Yubing，GONG Yulei，TAN Xingguo，et al. Probabilistic power flow calculation in microgrid based on Monte-Carlo simulation[J]. Transactions of China Electrotechnical Society，2011，26(S1)：274-278.

[14]刘明波，简淦杨，董萍. 孤岛微电网的随机潮流计算[J]. 华南理工大学学报(自然科学版)，2014，42(4)：13-18.

LIU Mingbo，JIAN Ganyang，DONG Ping. Stochastic power flow calculation of islanded microgrids[J]. Journal of South China University of Technology(Natural Science Edition)，2014，42(4)：13-18.

[15]ALLAN R N, BILLINTON R, SJARIEF I, et al. A reliability test system for educational purposes-basic distribution system data and results[J]. IEEE Transactions on Power systems, 1991, 6(2): 813-820.

[16]陈鹏伟，陶顺，肖湘宁，等. 主动配电网可靠性评估源荷模型改进及并行处理[J]. 电力系统自动化，2016, 40(18): 68-75.

CHEN Pengwei，TAO Shun，XIAO Xiangning，et al. Source-load model improvement and parallel computing for reliability evaluation of active distributed networks[J]. Automation of Electric Power Systems, 2016, 40(18): 68-75.

[17]杨俊友，王海鑫，邢作霞，等. 孤岛模式下潮流能发电系统协调控制策略[J]. 电工技术学报，2015，30(14)：551-560.

YANG Junyou，WANG Haixin，XING Zuoxia，et al. Coordination control strategy of tidal power generation in island grid[J]. Transactions of China Electrotechnical Society，2015，30(14)：551-560.

[18]孙孝峰,吕庆秋. 低压微电网逆变器频率电压协调控制[J]. 电工技术学报，2012，27(8)：77-84.

SUN Xiaofeng，LYU Qingqiu. Improved PV control of grid-connected inverter in low voltage micro-grid[J]. Transactions of China Electrotechnical Society，2012，27(8)：77-84.

[19]梁惠施，程林，刘思革. 基于蒙特卡罗模拟的含微网配电网可靠性评估[J]. 电网技术， 2011，35(10)：76-81.

LIANG Huishi，CHENG Lin，LIU Sige. Monte Carlo simulation based reliability evaluation of distribution system containing microgrids[J]. Power System Technology，2011，35(10)：76-81.

[20]XU X, MITRA J, WANG T, et al. Evaluation of operational reliability of a microgrid using a short-term outage model[J]. IEEE Transactions on Power Systems, 2014, 29(5): 2238-2247.

[21]王秀丽，武泽辰，曲翀. 光伏发电系统可靠性分析及其置信容量计算[J]. 中国电机工程学报，2014，34(1)：15-21.

WANG Xiuli，WU Zechen，QU Chong. Reliability and capacity value evaluation of photovoltaic generation systems[J]. Proceedings of the CSEE，2014，34(1)：15-21.

(编辑 景贺峰)

附录A

储能-负荷协调控制模型的约束条件如式(A1)所示。

(A1)

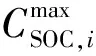
储能装置放电时，PSB-i(t)>0，t时段截止荷电状态为

(A2)

储能装置充电时，PSB-i(t)≤0，t时段截止荷电状态为

(A3)

式中：ηCi，ηDi分别为充电效率和放电效率；σi为储能装置每小时自放电率。

附录B

电力负荷具有时变性，长期实践验证，随机潮流计算中负荷的随机模型符合正态分布。但除了负荷固有的随机性外，不同类型负荷的负荷水平不同，为表征负荷的多样性，计及不同类型负荷的负荷水平，采用负荷模型如式(B1)所示。

PL(t)=PL0(t)+Pα(t)

(B1)

式中：PL0(t)为某类负荷日基本负荷水平序列t时刻的功率水平，该序列由典型日负荷曲线按固定步长或变步长划分而成，t∈[0, 24] h；Pα(t)为负荷波动分量，可利用正态分布随机抽样来模拟。

Power Quality Evaluation in Active Distribution Network Based on Its Operation Characteristics

SONG Mengqi, TAO Shun, CHEN Pengwei

(State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China)

When faults occur in active distribution network (ADN), the isolation of malfunctions can ensure continuous power supply for un-faulted region. Based on these active operation characteristics, this paper proposes an power quality evaluation method for ADN with considering the multi operation states of ADN. Firstly, the state duration of components is sampled, a sequence of the system state and duration can be further obtained, and the topology and parameter identification of network in each state are implemented. Then Latin hypercube sampling is adopted for loads and the distributed generation outputs, and the coordinated control between energy storage and loads is implemented considering the principle of power balance in the island mode, so that the power of the distributed generation, energy storage and loads can be obtained. Finally, we calculate the probabilistic power flow under each running state, statistically analyze the voltage amplitude results, and use the proposed indexes of voltage deviation risk and island node outage probability to evaluate the voltage quality. The application in the ADN test system based on RBTS-Bus2 proves the efficiencies of the proposed method.

active distribution network (ADN); probabilistic power flow calculation; power quality evaluation

国家自然科学基金项目(51207051)

TM 712

A

1000-7229(2016)12-0119-09

10.3969/j.issn.1000-7229.2016.12.016

2016-07-06

宋梦琪(1992)，女，硕士研究生，主要研究方向为主动配电网电能质量评估；

陶顺(1972)，女，博士，副教授，主要研究方向为智能配电网和电能质量等；

陈鹏伟(1992)，男，博士研究生，主要研究方向为电能质量、分布式发电技术与主动配电网技术。

Project supported by National Natural Science Foundation of China(51207051)