基于二层规划的交直流混合输电网最优潮流计算

范宏，陈斯，左路浩，周献远

(上海电力学院电气工程学院，上海市 200090)

基于二层规划的交直流混合输电网最优潮流计算

范宏，陈斯，左路浩，周献远

(上海电力学院电气工程学院，上海市 200090)

建立了交直流混合输电网等值数学模型，提出了交直流混合输电网最优潮流二层规划数学模型。该模型的上层目标函数为总燃料费用最小，变量为系统中有功与无功出力；下层目标函数为各节点电压偏移最小，变量为变压器分接头档位，上下层变量相互影响，交替迭代。采用跟踪中心轨迹内点法和萤火虫算法相结合的混合算法对该模型进行求解，上层模型利用跟踪中心轨迹内点法处理连续变量，能快速收敛至全局最优解；下层模型采用萤火虫算法求解，能较好处理离散变量。最后采用IEEE 30节点系统和IEEE 118节点系统为算例进行仿真计算，验证了该二层规划模型的有效性和正确性，对比了交流线路和直流线路功率传输方式，验证了直流系统输电的优势。

交直流混合输电；二层规划；最优潮流；内点法；萤火虫算法

0 引 言

随着我国±1 100 kV直流特高压输电线路和 1 000 kV交流特高压输电线路的建设，我国将逐渐形成以特高压输电线路为核心网架、交直流混合运行的坚强电网[1]。我国经济发达地区主要集中在江浙沪地区、广东沿海地区以及京津冀等地区，同时此类地区也是电力负荷中心，而能源聚集地主要集中在中西部和北部地区，因此，大容量远距离电能输送是未来研究的重点方向。高压交直流混联电网在输送容量上具有巨大优势[2]，已成为我国西电东送，北电南送的主要方式。随着特高压线路的建设，交直流电网优化运行面临新的挑战。

国内外已对交直流混联电网潮流计算[3-6]做了大量研究。传统最优潮流计算针对的主要对象是交流系统，典型的计算方法有线性规划法[7]、非线性规划法[8]及现代智能算法[9]。交直流混合输电网最优潮流计算方法是在纯交流输电网最优潮流计算的基础上加以改进而得的方法。文献[10]提出了一种求解大规模超高压交直流混合输电网最优潮流的方法，该方法利用现代内点法将交直流系统置于一个模型中统一求解，但对变压器变量作连续规整。文献[11]提出了利用模糊理论求解含柔性输电的交直流混联电网有功最优潮流的方法，实现了有功功率调度的最优分配。文献[12]提出了求解交直流互联电网多目标无功优化问题的帕累托最优解的方法，该方法能在短时间内处理大电网的优化问题。文献[13-14]将现代智能算法应用到交直流混合输电网最优潮流计算中，丰富了交直流最优潮流计算方法。

本文在总结交流输电网以及交直流混合输电网最优潮流算法的基础上，提出基于二层规划的交直流混合输电网最优潮流计算模型，并采用跟踪中心轨迹内点法和萤火虫算法相结合的混合算法进行求解，该混合算法能充分发挥内点法在处理非线性连续变量时收敛迅速的优势，同时又体现了萤火虫算法在处理离散变量时需调整参数少以及寻优能力强的优势。

1 交直流混合输电网等值数学模型

1.1 模型建立

在传统纯交流输电网中加入直流系统构成交直流混合输电网，直流系统通过换流站与交流电网联接。本文交直流混合系统连接形式采用文献[15]中提出的交直流混合输电系统，如图1所示，其中直流输电系统为两端系统，交流系统与直流系统通过换流变压器交换功率。交流系统包含发电机、交流变压器、交流输电线路、无功功率补偿器等，直流系统主要包括换流变压器、整流器/逆变器、直流输电线路等。

图1中Udm为整流侧直流电压；ktm为整流侧换流变压器变比；Utm为整流侧换流变压器连接的交流母线电压；Udn为侧变器直流电压；ktn为逆变侧换流变压器变比；Utn为逆变侧换流变压器连接的交流母线电压。

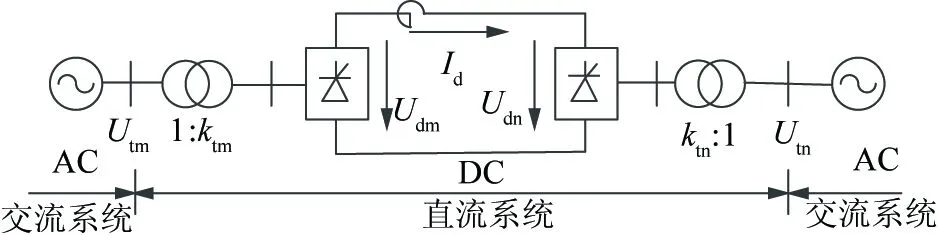
图1 交直流系统连接图

交直流输电网正常运行时，忽略换流变压器有功功率损耗，对于多桥换流器的直流系统，整流侧直流电压与换流变压器连接的交流母线电压之间的转换关系为：

(1)

(2)

(3)

式中：ntm为换流器数量；θdm为整流器触发滞后角；Xcm为整流侧换流变压器等值电抗；Id为直流线路电流；kγ为换相效应引入系数，常取0.995；φdm为整流器功率因数；Itm为整流侧换流变压器一次侧线电流基波分量。

逆变侧直流电压与换流变压器连接的交流母线电压之间的转换关系为：

(4)

(5)

(6)

式中：ntn为换流器数量；θdn为整逆变器触发滞后角；Xcn为逆变侧换流变压器等值电抗；φdn为逆变器功率因数；Itn为逆变侧换流变压器一次侧线电流基波分量。

对于两端直流系统，整流侧与逆变侧之间的电流为Id，则直流网络方程为

(7)

式中R为直流输电线路的电阻。

1.2 直流系统与交流系统标幺转换

在最优潮流计算中，由于传统交流系统中各运行参数采用了标幺制，故在交直流输电网中直流系统各运行参数与其对应也应采用标幺制[16]。直流系统各个各运行参数基准值采用下标DB表示，则在直流系统中，各运行参数的基准值有如下关系：

(8)

式中：UDB为直流侧基准电压；RDB为直流线路电阻；IDB为直流线路电流基准值；PDB为直流侧功率基准值。

交流系统中各运行参数基准值采用下标B表示，则交流物理量与直流物理量之间的关系为

(9)

式中：SB为交流节点功率；UB为交流侧电压基准值；IB为交流侧电流基准值；nt为换流器数量；ktb为换流变压器变比。

对式(1)-(6)两端除以相应的基准值，则得到直流系统的标幺方程如下：

Ud*=kt*Ut*cosθd-Xt*Id*

(10)

Ud*=kγkt*Ut*cosθφ

(11)

It*=kγkt*Id*

(12)

式中：Ud*为换流器直流电压标幺值；kt*为换流变压器变比标幺值；Ut*为整流侧/逆变侧换流变压器连接的交流母线电压基准值；θd为换流器触发滞后角；Xt*为换流变压器等值电抗标幺值；Id*为直流线路电流标幺值；θφ为换流器功率因数角；It*为换流变压器一次侧线电流基波分量标幺值。

2 二层规划法求解交直流输电网最优潮流

2.1 二层规划数学模型

二层规划法是通过分层形成递阶结构解决数学问题的建模方法[17]，是多层规划中求解最优问题的最常用数学方法[18]。二层规划法对求解多目标、多层次、多决策变量的优化问题具有较强的针对性。二层规划模型由上层模型和下层模型构成，上层和下层模型均有其相应的目标函数和约束条件。上层模型与下层模型相互影响、相互联系，上层模型最优值受下层决策变量的影响，同时下层模型的最优值受上层模型解的约束。二层规划数学模型为：

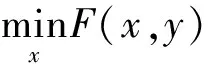
(13)

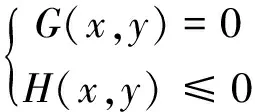
(14)

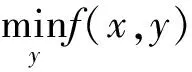
(15)

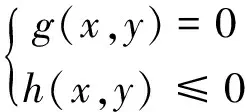
(16)

式中：x、y分别为上下层模型决策变量；F(x,y)、f(x,y)分别为上下层目标函数；G(x,y)、g(x,y)分别为上下层目标函数的等式约束；H(x,y)、h(x,y)分别为上下层目标函数的不等式约束。

交直流输电网最优潮流计算是一个非线性、多约束的全局优化问题，因此本文将二层规划理论运用到交直流输电网最优流潮流计算中，充分利用最优潮流计算中各变量与目标函数之间的关系，从整体最优角度出发，充分考虑整体最优与部分最优的上下层反馈关系，寻求最优解。

本文二层规划法的交直流最优潮流数学模型中，上层模型以发电成本最小为目标函数，下层模型以交流系统母线电压以及直流系统换流器电压偏差值最小为目标函数。

2.2 交直流输电网最优潮流计算方法

交直流输电网最优潮流二层规划模型中，上层模型目标函数数学模型为

minF=aP2+bP+c

(17)

式中：a、b、c分别为发电成本二次系数、一次系数以及常数项；P为发电机有功功率。

上层模型决策变量为各发电机有功功率、无功功率以及无功电源出力，上层模型等式约束包括式(1)—(6)所描述的直流系统物理量之间的等式方程以及节点有功功率和无功功率平衡方程：

(18)

式中：Pi、Qi分别为交流节点i注入的有功功率和无功功率；Ui、Uj分别为交流节点i和j的节点电压；Gij、Bij、θij分别为交流节点i和j之间的电导、电纳和相角差；Udk、Idk、φdk分别为直流系统换流器电压、直流线路电流、换流器功率因数；pdk为直流系统系数，当节点表示纯交流节点时pdk=0，当节点连接整流器时pdk=1，当节点连接逆变器时pdk=-1。

不等式约束如式(19)—(25)所示。

发电机有功功率与无功功率上下限约束：

(19)

(20)

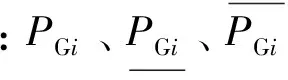
无功补偿容量上下限约束：

(21)

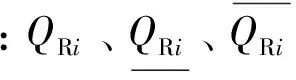
交流线路与直流线路传输功率上下限约束：

(22)

(23)

交流线路功率因数上下限约束：

(24)

式中θij为交流线路功率因数角。

整流器/逆变器触发角和熄弧角上下限约束：

(25)

上层模型决策变量均为连续变量，采用跟踪中心轨迹内点法对上层模型进行计算。跟踪中心轨迹内点法能够保证在寻优迭代时变量保持在可行域内搜索迭代点，当有解接近可行域的边界时，目标函数会由于障碍函数中值的增大而返回可行域继续迭代[19]，迭代点在可行域内寻优的过程中改变松弛变量和拉格朗日乘子不断接近最优解。跟踪中心轨迹内点法的计算流程如图2所示。

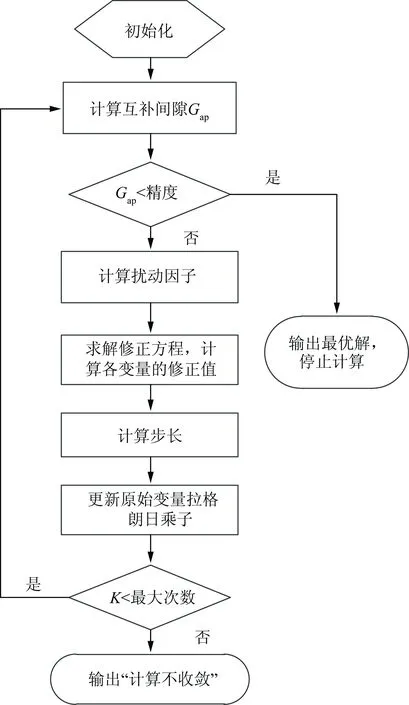
图2 内点法计算流程图

下层模型目标函数数学表达式为

(26)

式中：UiN、Uid、Uidn分别为交流系统节点电压基准值、直流系统电压、直流系统电压基准值；n、nd分别为交流系统节点数和直流系统换流器个数。

下层模型等式约束为式(1)—(6)所描述的直流系统等式约束以及式(27)所示交流系统节点电压等式约束：

(27)

式中：Pij、Qij分别为交流变压器流过的有功功率和无功功率；kt为节点i、j之间交流变压器变比；Rij、Xij分别为节点i、j之间交流线路电阻与电抗。

不等式约束如式(21)、(28)—(29)所示。

交流节点电压上下限约束以及直流侧电压上下限约束：

(28)

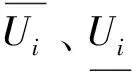
变压器变比上下限约束：

(29)

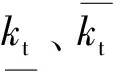
下层模型决策变量为交流系统中各变压器分接头档位以及直流系统中换流变压器分接头档位，该决策变量均为离散变量，采用萤火虫算法[20]进行求解。萤火虫算法是一种新型生物群智能算法，在下层模型的计算过程中，将模型目标函数转化为萤火虫的相对亮度，在寻优过程中，亮度大的萤火虫吸引亮度小的萤火虫向其靠近，同时更新亮度较小的萤火虫位置，最终得到最优解。萤火虫算法的计算流程如下：

步骤1：设定参数，随机设定萤火虫的初始位置，选取每组萤火虫的最大亮度值；

步骤2：计算萤火虫的相对亮度和相对吸引度，判断每个断萤火虫的移动方向；

步骤3：根据萤火虫的移动方向，计算萤火虫的移动位置，更新萤火虫的相对亮度和相对吸引度；

步骤4：判断是否达到搜索精度，若达到，输出最优值，若未达到，继续搜索，直到满足条件。

在交直流二层规划模型中，上层模型决策变量为各发电机有功功率、无功功率以及无功电源出力，各节点有功功率、无功功率以及线路传输功率对下层模型中的电压产生影响，而下层目标函数中各节点电压反馈到上层模型中，对上层模型中各节点有功功率和无功功率产生影响。模型中上层与下层各变量相互反馈，相互影响。利用二层规划算法求解交直流混合电网最优潮流的流程如图3所示。

3 算例分析

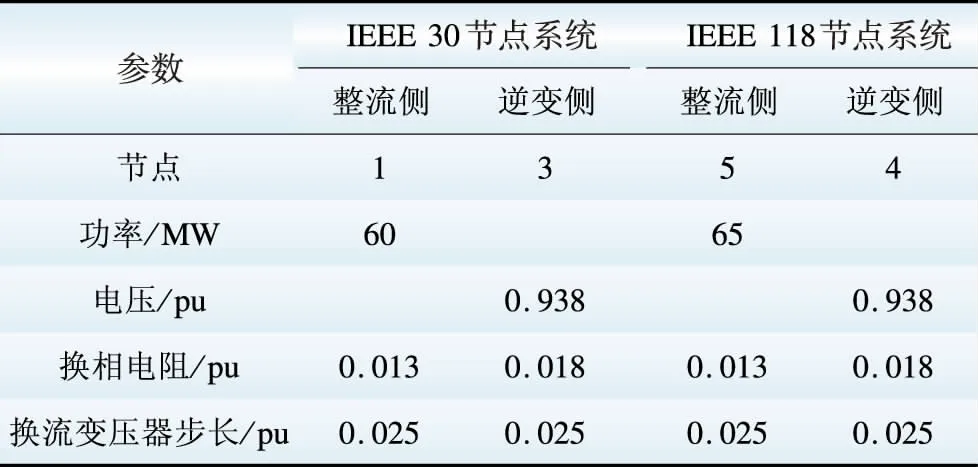
本文以IEEE 30标准节点系统和IEEE 118标准节点系统为例，其中IEEE 30节点系统将节点1与节点3之间的交流线路替换为直流输电系统，形成含有直流输电系统的交直流混合电网，其中节点1为整流侧，节点3为逆变侧。IEEE 118标准节点系统将节点5与节点4之间的交流线路替换为直流输电系统，其中节点5为整流侧，节点4为逆变侧。直流系统中，

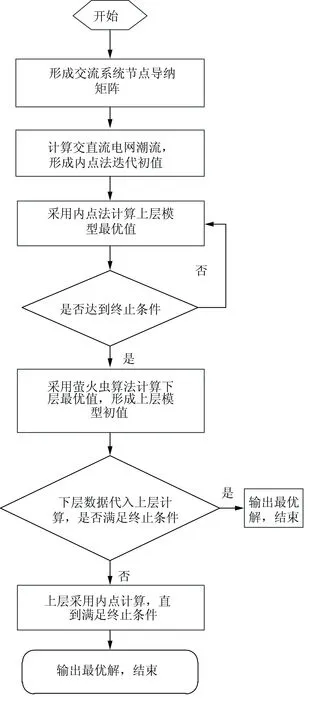
图3 二层规划算法计算流程图

整流侧控制方式为定功率控制，逆变侧控制方式为定电压控制。交流系统与直流系统中有功功率与无功功率采用有名值，其余量均采用标幺值。直流系统各参数如表1所示。

表1 直流系统参数

Table 1 DC system parameter

3.1 IEEE 30节点系统算例

以IEEE 30节点系统为例，加入直流输电系统后，该系统具有发电机6台，交流线路36条，直流线路1条，分别采用二层规划算法和遗传算法对IEEE 30节点系统进行求解。优化前后各电源出力与发电总费用对比如表2所示，优化后各母线电压最大偏移值如表3所示，优化后直流系统各运行参数如表4所示。

表2 优化前后发电机出力及费用

Table 2 Generator output and cost before/after optimization

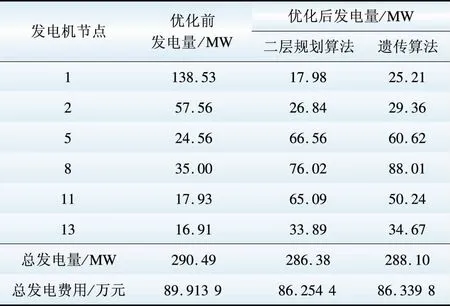
表3 优化后各母线电压最大偏移值

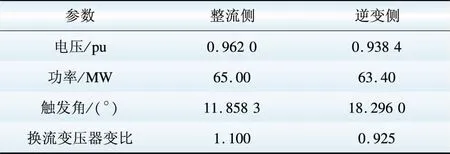
表4 优化后直流系统各运行参数

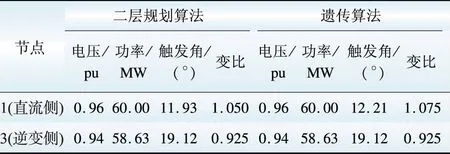
由上述结果可知，采用优化算法后，整个系统总发电量和总费用较优化前有所下降，二层规划算法结果相比遗传算法结果更优。从电压偏移角度来看，二层规划算法最大偏移值较遗传算法小，二层规划算法投入无功功率较多，故最低电压较遗传算法最低电压有所提升。由于直流系统整流侧采用了定功率控制，逆变侧采用了定电压控制的方式，在直流系统优化过程中，上述算法计算结果差别较小。

分析比较优化前后交流系统各参数变化量如表5所示。在IEEE 30节点交直流电网中，将直流系统中直流输电线路电阻标幺值设为0.045 2，与替换前的交流线路电阻标幺值保持一致。在交直流混合输电网中，对直流输电线路采用不同输送功率，采用二层规划算法分别对上述不同功率传输方式进行计算，对比分析优化后系统发电量、发电费用、系统网损以及直流线路损耗，计算结果如表6所示。

表5 纯交流系统优化前后参数

Table 5 Parameters of AC system before/after optimization

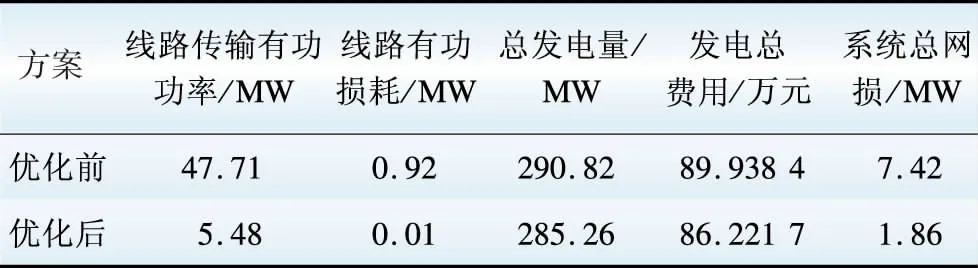
表6 不同直流输送率的系统各参数

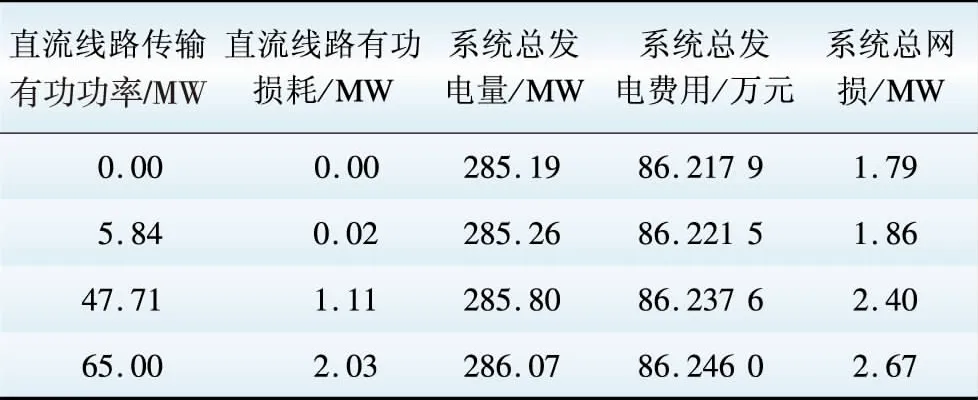
通过优化后，纯交流系统与交直流混合系统总发电量、总发电费用与总网损均有所下降。纯交流系统在优化后，单条线路自然潮流将会是定值，但直流输电可根据需要调节输电线路传输功率，系统总发电费用没有较明显增长，针对目前我国远距离大容量传输电能，直流输电具有较明显优势。

3.2 IEEE 118节点系统算例

以IEEE 118节点系统为例，加入直流输电线路后，该系统具有发电机16台，交流线路178条，直流线路1条。利用二层规划算法对含直流系统的IEEE 118节点交直流系统进行求解。优化前后各电源出力与发电总费用对比如表7所示，优化前后各母线电压最大偏移值如表8所示，优化后直流系统各运行参数如表9所示。

由上述结果可知，对于IEEE 118节点系统，优化后整个系统发电量与发电费用较优化前均明显下降，优化后电压偏移最大值较优化前有明显降低，优化后无功投入量较优化前有较明显的降低，使得优化后最高电压较优化前有所降低，直流系统均运行在安全范围内。通过大节点系统的仿真计算，验证了二层规划算法求解交直流混合电网最优潮流的有效性。

表7 优化前后发电机出力及费用

Table 7 Generator output and cost before/after optimization

表8 优化前后各母线电压最大偏移值及无功功率投入量

表9 优化后直流系统各运行参数

4 结 论

(1)二层规划算法中，内点法处理连续变量具有优势，可减少计算时间；萤火虫算法具有搜索速度快、效率高，算法简单的特点，对于处理变压器分接头档位这一离散变量具有优势；混合算法能兼顾2种算法优势。

(2)优化后节点电压较优化前有明显提升，无功投入量均在合理范围内。优化后总发电量和总发电费用均有明显下降。直流系统中各运行参数均处在安全运行范围内。

(3)直流系统不同传输容量对最优潮流优化结果影响较小，直流线路传输容量逐渐增大时，系统总发电量与发电费用无明显上升。结果表明在不影响系统安全稳定的情况下，直流输电适合点对点大容量传输功率。

[1]刘振亚，张启平．国家电网发展模式研究[J]．中国电机工程学报，2013，33(7)：1-10，25．

LIU Zhenya，ZHANG Qiping．Study on the development mode of national power grid of China[J]．Proceedings of the CSEE，2013，33(7)：1-10，25．

[2]姚良忠，吴婧，王志冰，等．未来高压直流电网发展形态分析[J]．中国电机工程学报，2014，34(34)：6007-6020．

YAO Liangzhong，WU Jin，WANG Zhibing，et al．Pattern analysis of future HVDC grid development [J]．Proceedings of the CSEE，2014，34(34)：6007-6020．

[3]谭涛亮，张尧．计及直流控制方式转换和换流变变比调整的交直流潮流算法研究[J]．电力系统保护与控制，2011，39(1)：40-45，52．

TAN Taoliang，ZHANG Yao． Study on AC/DC power flow algorithm considering the switching of DC control mode and converter transformer ratio[J]．Power System Protection and Control，2011，39(1)：40-45，52．

[5]覃智君，侯云鹤，吴复立．大规模交直流系统潮流计算的实用化模型[J]．中国电机工程学报，2011，31(10)：95-101．

TAN Zhijun，HOU Yunhe，WU Fuli．Practical model for large-scale AC-DC system power flow calculation[J]．Proceedings of the CSEE，2011，31(10)：95-101．

[5]BEERTEN J，COLE S，BELMANS R．Generalized steady-state VSC MTDC model for sequential AC/DC power flow algorithms[J]．IEEE Transactions on Power Systems，2012，27(2)：821-829．

[6]张彦涛，秦晓辉，周勤勇，等．基于交直流解耦的超大规模交直流混合电网潮流计算可行解获取方法的研究[J]．中国电机工程学报，2015，35(24): 6275-6282．

ZHANG Yantao，QIN Xiaohui，ZHOU Qinyong，et al．Study on the acquisition method of the feasible solution for power flow calculation of large-scale power grids based on AC/DC decoupling[J]．Proceedings of the CSEE，2015，35(24)：6275-6282．

[7]STTOT B，MARINHO J L．Linear programming for power system network security application[J]．IEEE Transaction on Power Systems，1979，98(3)：837-848．

[8]WEI H，SASAKI H， KUBOKAWA J, et al．An interior point nonlinear programming for optimal power flow problems with a novel data structure[J]．IEEE Transactions on Power Systems，1998，13(3)：870-877．

[9]韩晓慧，王联国．输电网优化规划模型及算法分析[J]．电力系统保护与控制，2011，39(23)：143-148,154．

HAN Xiaohui，WANG Lianguo．Review of transmission network optimal planning model and algorithm[J]．Power System Protection and Control，2011，39(23)：143-148,154．

[10]李滨，韦化，阳育德，等．大规模超高压交直流系统最优潮流的研究[J]．现代电力，2010，27(4)：1-6．

LI Bin，WEI Hua，YANG Yude，et al．The optimal power flow of the large-scale extra high voltage AC/DC power systems[J]．Modern Electric Power，2010，27(4)：1-6．

[11]邓健俊，文安，魏承志，等．含柔性直流输电的交直流并列系统有功潮流优化方法[J]．电力系统保护与控制，2014，42(11)：118-123．

DENG Jianjun，WEN An，WEI Chengzhi，et al．An optimization method for active power flow in AC/VSC-HVDC parallel transmission systems[J]．Power System Protection and Control，2014，42(11)：118-123．

[12]李清，刘明波，杨柳青．求解交直流互联电网多目标无功优化问题的INNC法[J]．中国电机工程学报，2014，34(7)：1150-1158．

LI Qing，LIU Mingbo，YANG Liuqing．INNC method applied to multi-objective reactive power optimization in AC/DC interconnected power grid[J]．Proceedings of the CSEE，2014，34(7)：1150-1158．

[13]周孝法，陈陈，杨帆，等．基于自适应混沌粒子群优化算法的多馈入直流输电系统优化协调直流调制[J]．电工技术学报，2009，24(4)：193-201．

ZHOU Xiaofa，CHEN Chen，YANG Fan，et al．Optimal coordinated HVDC modulation based on adaptive chaos particle swarm optimization algorithm in multi-infeed HVDC transmission system[J]．Transactions of China Electrotechnical Society，2009，24(4)：193-201．

[14]彭磊，张建平，吴耀武，等．基于GA、PSO结合算法的交直流系统无功优化[J]．高电压技术，2006，32(4)：78-81．

PENG Lei，ZHANG Jianping，WU Yaoping，et al．Reactive power optimization of hybrid AC/HVDC power system based on genetic algorithm and particle swarm optimization[J]．High Voltage Engineering，2006，32(4)：78-81．

[15]郑超，盛灿辉，郭小江，等．实用高压直流输电稳态模型及潮流算法解析[J]．电网技术，2011，35(03)：57-62．

ZHENG Chao，SHENG Canhui，GUO Xiaojiang，et al．Analysis on practicable steady state model of HVDC power transmission and corresponding power flow algorithm[J]．Power System Technology，2011，35(3)：57-62．

[16]郑华，李晖，肖晋宇，等．大规模交直流电网最优潮流模型与算法研究[J]．中国电机工程学报，2015，35(9)：2162-2169．

ZHENG Hua，LI Hui，XIAO Jinyu，et al．Research on model and algorithm for optimal power flow of large-scale high voltage direct current transmission system[J]．Proceedings of the CSEE，2015，35(9)：2162-2169．

[17]WANG Y，JIAO Y C，LI H．An evolutionary algorithm for solving nonlinear bi-level programming based on a new constraint-handling scheme[J]．IEEE Transactions on Systems，Man，and Cybernetics，Part C (Applications and Reviews)，2005，35(2)：221-232．

[18]王淑芬，万仲平，樊恒，等．基于二层规划的无功优化模型及其混合算法[J]．电网技术，2005，29(9)：22-25．

WANG Shufen，WAN Zhongping，FAN Heng，et al．Reactive power optimization model and its hybrid algorithm based on bi-level programming[J]．Power System Technology，2005，29(9)：22-25．

[19]姚煜，蔡燕春．离散粒子群与内点法结合的电力系统无功优化[J]．电力系统保护与控制，2010，38(3)：48-52．

YAO Yu，CAI Chunyan．A hybrid strategy based on DPSO and IPM for optimal reactive power flow[J] ．Power System Protection and Control，2010，38(3)：48-52．

[20]陈海东，庄平，夏建矿，等．基于改进萤火虫算法的分布式电源优化配置[J]．电力系统保护与控制，2016，44(1)：149-154．

CHEN Haidong，ZHUNAG Ping，XIA Jiankuang，et al．Optimal power flow of distribution network with distributed generation based on modified firefly algorithm[J]．Power System Protection and Control，2016，44(1)：149-154．

(编辑 张小飞)

Optimal Power Flow of AC-DC Power Grid Based on Bi-Level Programming Method

FAN Hong,CHEN Si, ZUO Luhao, ZHOU Xianyuan

(School of Electrical Engineering, Shanghai University of Electric Power, Shanghai 200090, China)

This paper establishes the equivalent mathematical model of AC-DC power grid, and proposes the bi-level programming mathematical model for the optimal power flow (OPF) of AC-DC power grid. The upper objective function of the bi-level programming model is the minimization of total fuel costs, and sets the active power and reactive power as variables; the lower objective function is the minimum voltage offset between different nodes, and sets the taps position of transformer as variables. The upper and lower variables are interactional, alternative and iterative. We adopt the hybrid algorithm including the interior point method with tracking center path and the firefly algorithm to solve this model. The interior point method is used in the upper model, which can converge to the global optimal solution in short time. At the same time the firefly algorithm is used in the lower model, which can deal with discrete variables better. Finally, the simulation results of the IEEE 30 nodes system and IEEE 118 nodes system verify the validity and correctness of the bi-level programming algorithm. Through the power transmission way comparison between AC and DC line, the advantage of DC power transmission system is verified.

AC-DC hybrid transmission; bi-level programming; optimal power flow; interior point method; firefly algorithm

国家自然科学基金项目(51307104)

TM 732

A

1000-7229(2016)12-0089-07

10.3969/j.issn.1000-7229.2016.12.012

2016-06-25

范宏(1978)，女，博士，副教授，主要研究方向为电力系统优化运行，电力系统仿真计算，电网规划等;

陈斯(1989)，男，硕士研究生，主要研究方向为电力系统优化运行，电力系统仿真计算等;

左路浩(1991)，男，硕士研究生，主要研究方向为电力系统规划，电力市场等;

周献远(1990)，男，硕士研究生，主要研究方向为新能源对电力系统的影响，电力系统仿真计算等。

Project supported by National Natural Science Foundation of China (51307104)