基于多场景随机规划的电力系统生产模拟方法

姚力，王秀丽，肖汉，傅旭，李彬，杨攀峰

(1．西安交通大学电气工程学院，西安市 710049；2．西南电力设计院有限公司，成都市610000；3．西北电力设计院有限公司，西安市 710049 )

基于多场景随机规划的电力系统生产模拟方法

姚力1，王秀丽1，肖汉2，傅旭3，李彬2，杨攀峰3

(1．西安交通大学电气工程学院，西安市 710049；2．西南电力设计院有限公司，成都市610000；3．西北电力设计院有限公司，西安市 710049 )

针对电力系统生产模拟中新能源不确定性问题,引入多场景随机规划理论，研究了含新能源电力系统的生产模拟方法。在时间尺度为周的生产模拟中，由多场景方式刻画新能源不确定性，建立随机规划数学模型模拟系统运行，并采用基于Benders分解的算法求解该模型。通过实际系统算例，计算了新能源年弃电率、火电盈余装机容量等指标，比较了不同求解方法下生产模拟的结果，研究了旋转备用率对新能源接纳能力的影响，结果表明所提出的生产模拟方法能够计算系统运行相关指标，所采用的算法相对于直接调用数学软件求解有一定的优势。另外，给出了旋转备用率与新能源弃电率、接纳电量之间的关系。

生产模拟；随机规划；新能源接纳能力

0 引 言

电源规划作为电力系统规划的重要内容，会对工业进步、居民日常生活等产生重要影响。当前，环境污染形势日益严峻，促进以水电、风电、光伏等为代表的清洁能源发展已经成为全社会的共识。另一方面，我国经济发展逐渐步入新常态，在“去产能、促转型”的背景下，调整电源结构、加强电源规划指导作用的呼声渐起。因此评价各类型电源规模的合理性，进而确定合适的电源结构是近年来研究的热点，而评价电源规划方案的关键在于通过生产模拟方法获取规划人员所关心的评价指标。生产模拟方法主要包括确定性生产模拟方法和随机生产模拟方法。确定性生产模拟[1-5]方法不考虑常规机组的随机停运故障：文献[1]针对江苏电网，采用了考虑网架约束的逐日时序生产模拟方法，得到了投资成本和运行成本最小的电源规划方案；文献[2]提出了一种年弃风电量的快速计算方法，分析了风电装机容量和弃风比例之间的关系；文献[3]研究了调峰和电网输送功率对新能源接纳电量的影响；文献[4]分析了低碳要素对电源规划结果的影响；文献[5]采用时序仿真计算了系统年新能源接纳能力。随机生产模拟[6-11]方法则考虑了机组的随机停运故障影响：文献[9]采用等效电量频率法，刻画了风电波动对机组启停频率期望的影响；文献[10]在随机生产模拟中考虑了风火联合外送；文献[11]研究了含光伏系统的随机生产模拟方法。

现有生产模拟方法的研究存在以下不足：(1)新能源不确定性建模有待提高，在一条确定的新能源出力曲线下安排运行方式、计算新能源接纳指标等于将新能源出力确定化，忽略了随机特性；(2)生产模拟的结果为电源规划、调度运行提供的指导不足。生产模拟应当反映出各类型电源建设规模是否合适，如何调整电源规划方案。通过模拟运行，判断系统调峰资源是否充足，各时刻调峰问题是否严重，为运行部门提供优化运行建议，以提高新能源接纳能力。

本文针对现有研究的不足，引入随机规划理论，研究了含新能源电力系统的生产模拟方法。通过逐周的生产模拟，得到新能源年弃电率、火电盈余装机容量等指标，作为判断新能源、火电装机规模是否合适的依据。在新能源不确定性建模方面，以多场景的方式刻画新能源不确定性，在各周分别建立优化模型以模拟系统运行，并利用基于Benders分解的算法求解模型。在为电源规划、调度运行提供指导方面，通过实际算例，安排各类型机组优化运行方式，指出系统调峰能力不足时刻，给出各周新能源弃电的概率信息。年新能源弃电率、火电盈余装机容量等指标可以为调整电源规划方案提供依据。

1 多场景随机规划

1.1 两阶段随机规划

本文讨论的随机规划问题指的是两阶段随机规划问题，如式(1)、(2)所示：

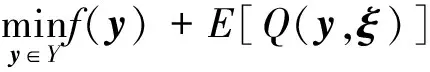
(1)

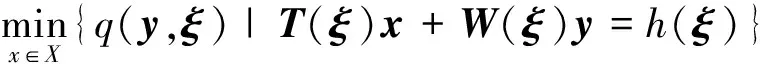
(2)

式中：y是第1阶段的决策变量；Q(y,ξ)是第2阶段问题的最优解，ξ是不确定因素对应的向量；x是第2阶段的决策变量；T()、W()是包含不确定因素的矩阵。第一阶段在ξ实现之前，制定决策y。在第二阶段，当ξ实现后，根据ξ的具体情况制定决策x。一般认为不确定因素ξ满足一定已知的概率分布，如ξ包含有限数量的实现ξ1，...，ξK，对应概率p1，...，pK，每个实现称为一个场景。这样，第一阶段的目标函数有如下形式：

(3)

1.2 新能源场景生成

新能源出力曲线完全依赖于自然条件，如风速、光照强度，其本质是时间序列。由于风速、光照等气象因素存在不确定性，新能源出力曲线是不确定的，所以从概率的观点来看，每条曲线是以一定概率实现的，分别表征了新能源出力的一种实现可能，所有曲线组成了场景集合S。第s个场景下，第i个新能源场站出力序列表示为[wi,1,s,wi,2,s, …，wi,T,s]T，s∈S，wi,t,s表示第s个场景下，第i个新能源场站在t时刻的出力。向量 [p1,p2, …,pj,…,ps]T中各元素表示各个场景的概率，pj是第j个场景发生的概率，所有场景的概率和为1。

研究表明，新能源具有季节特性。以西北某省为例，其2012年各季节风电出力概率分布如图1所示，明显看出春夏风电出力较大而秋冬较小，所以分季节生成新能源出力场景。首先，收集新能源的年历史新能源出力曲线，并标幺化处理。给定规划年的新能源装机规模后，将其作为基准值，得到模拟的新能源出力曲线。分季节统计新能源各周的出力曲线，认为某季节下每条曲线的概率都相等，这样就能得到4个季节的场景集合。最后，当进行某季节内的周生产模拟时，将采用该季节出力场景集合，即同一季节下每周生产模拟采用的新能源出力场景集合都相同。关于新能源出力场景生成，还需要说明三点：(1)风电和光伏分别生成出力场景；(2)如果场景数太多，可通过场景削减或场景聚类[12]的方式减少场景数量以减轻计算负担；(3)出力场景在全年的电量期望值之和与提供的年历史曲线总电量一致。

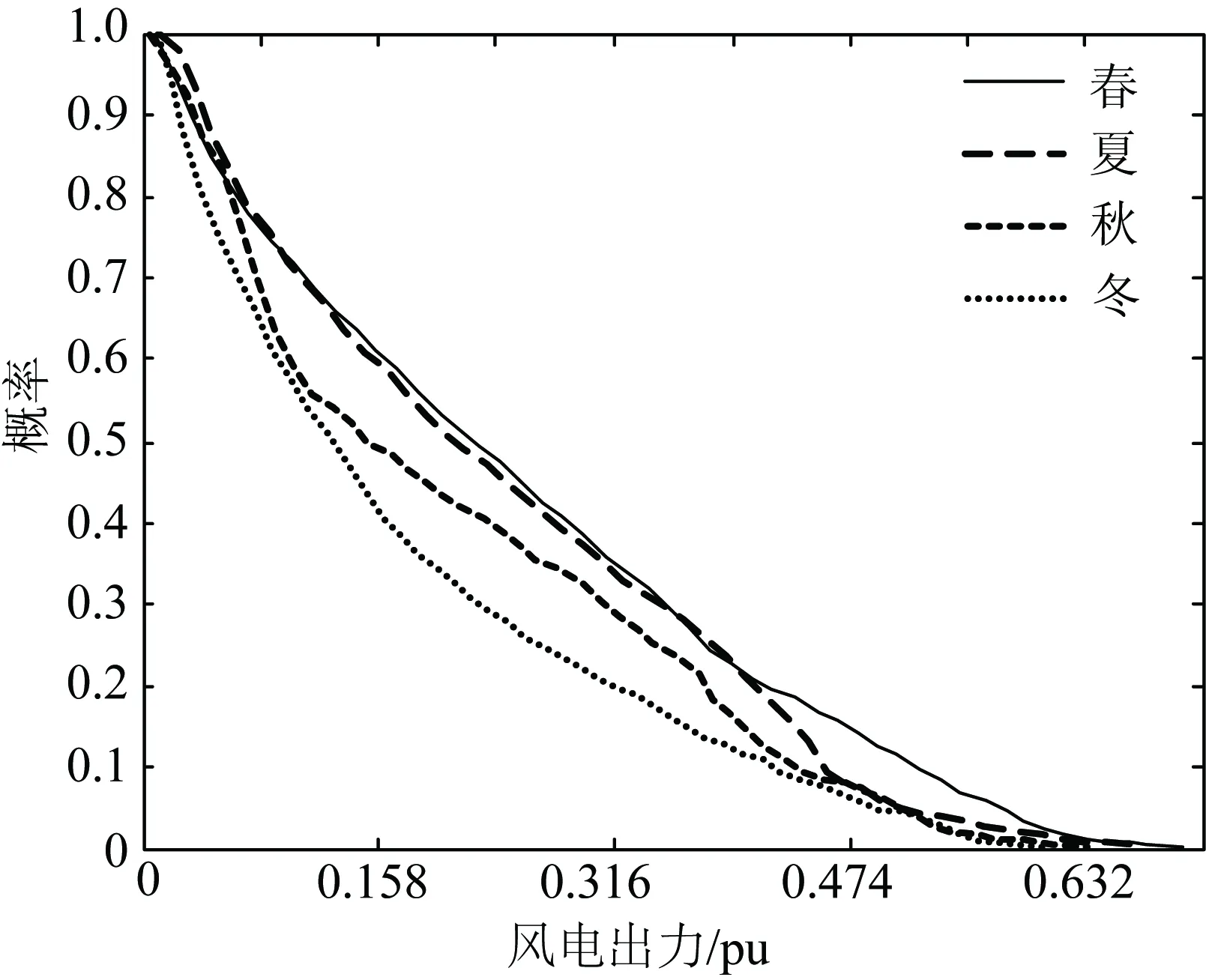
图1 西北某省2012年风电出力概率分布

2 生产模拟方法

2.1 数学模型

在给定某年的电源结构，并安排好常规机组的检修计划后，通过逐周的生产模拟，得出该年的计算指标。采用周而不采用月和日作为时间尺度，一方面是因为可以反映机组在1周内随负荷波动而发生的状态变化，另一方面，以周为时间尺度在计算效率上是能够接受的。

周生产模拟是在1周之内安排合理的运行方式，使得系统运行总成本最小，目标函数为

(4)

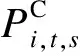
目标函数优化的是各场景下发电成本的数学期望与火电机组的状态成本，尽管新能源出力场景有多个，但火电的开机方式只有1个，这样便于运行人员安排火电开停机计划。水电和新能源的发电成本几乎可以忽略，所以为了使运行费用最小，应当尽可能接纳水电和新能源。除了目标函数，数学模型还有若干约束，如下详述。

(1)电力平衡约束：

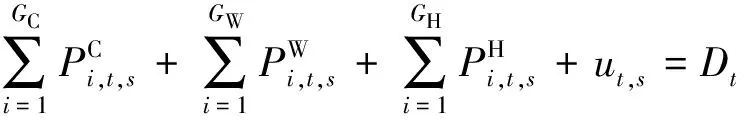
(5)

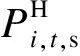
(2)火电出力约束：

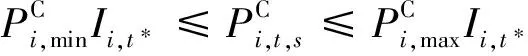
(6)

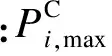
(3)火电最小开机时间约束：

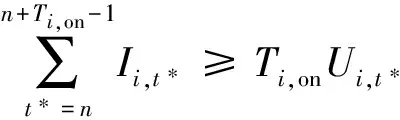
(7)

式中Ti,on是第i台火电的最小开机时间，天。同理，还有最小停机时间约束，这里不再赘述。

(4)启动状态约束：

Ii,t*-Ii,t*-1≤Ui,t*,∀i,t*=1,2,…,T*

(8)

(5)停机状态约束：

Ii,t*-1-Ii,t*≤Di,t*,∀i,t=1,2,...,T*

(9)

(6)新能源出力约束：

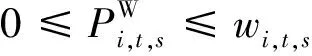
(10)

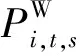
(7)水电出力约束：

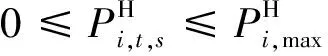
(11)

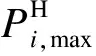
(8)水电电量约束：

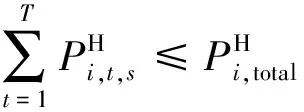
(12)

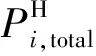
(9)旋转备用约束：

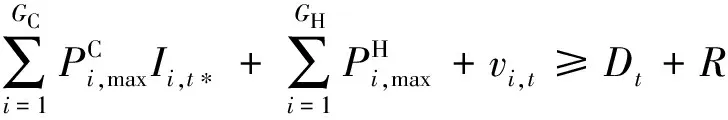
(13)

式中R是系统的旋转备用需求容量。

除了上面的约束外，还有火电爬坡约束，机组启停次数限制约束，直流潮流约束等，可根据需要加入模型。考虑到对规划年逐周进行生产模拟，所以火电的开机方式在周与周之间具有耦合性。前一周结束后，将最后的开机方式作为下一周的初始开机方式。

2.2 基于Benders分解的求解方法

在系统规模较大、场景数量较多时，利用Cplex[13]等数学软件直接求解模型存在计算效率低的问题。在保证计算精度的前提下，为加快求解速度，本文采用了基于Benders分解的方法求解周生产模拟模型。首先，将模型(3)—(13)写成简化形式：

(14)

(15)

式中：xs为与场景s有关的连续变量向量，如发电机出力、失负荷等；y为火电机组状态变量向量，元素包括机组运行状态、启停状态，其实质是整数变量向量；cs与d分别是xs和y的系数列向量。根据约束中变量的性质，将约束式(5)—(13)分为以下3类：约束Ay≤b是整数变量约束，对应了式(7)—(9)；约束Esxs+Fsy≤hs是整数变量、连续变量耦合约束，对应式(6)、(13)；约束Msxs≤ls是各场景连续变量约束，对应式(5)、(10)—(12)。因此，式(14)—(15)可以写成如式(16)—(17)所示的两阶段等价形式：

mindTy+E[Qs(y)]

(16)

Ay≤b

(17)

Qs(y)是下面优化问题的最优解，E[]表示求数学期望。

(18)

(19)

第1阶段的目标是优化与火电状态有关的费用dTy以及对运行费用期望值的估计E[Qs(y)]。第二阶段的目标是在给定开机方案下，使得所有场景运行费用的期望值最小。事实上，两阶段的结构与调度运行的思路是一致的。首先综合新能源出力的各种可能性，提前确定机组开机计划，然后根据新能源的实际出力，制定相应的各类型电源出力方案。

利用两阶段模型结构上的特点，将两阶段问题分成主问题和多个场景子问题。主问题是一个整数规划问题，对应了第一阶段，求解之后得到所有火电的出力状态，即模型的整数变量；子问题是若干相互独立的线性规划问题，每个线性规划都对应了一个场景，各场景排好出力计划后会给予主问题反馈信息，主问题将重新求解安排出新的机组开机计划。主问题和子问题之间反复迭代，直到整体经济性达到最优。下面以第k次迭代为例，分别介绍主问题和子问题的求解过程。

主问题模型如式(20)—(21)所示。模型目标函数中的θs是引入的中间变量，约束一方面包含整数变量约束Ay≤b，另一方面包含了迭代求解子问题产生的切割。在每次迭代中，求解1个场景的线性规划问题就能够返回1条切割。

(20)

(21)

主问题的计算结果是整体问题最优解的下界LB，随着迭代次数的增加，主问题中切割数将增多，下界逐步上升。

(22)

(23)

根据线性规划的强对偶理论[14]，式(22)、(23)的对偶问题为

(24)

(25)式中λs,k和γs,k分别是约束Esxs+Fsy≤hs和Msxs≤ls的对偶乘子向量。由强对偶理论知，式(22)、(23)和式(24)、(25)的计算结果相同，均为Qs。求解式(24)、(25)后，产生1条切割如式(26)所示，加入主问题中。

(26)

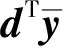
算法框图如图2所示，将模型分解为主问题和子问题，使得各部分的计算规模相对原问题都极大减小，

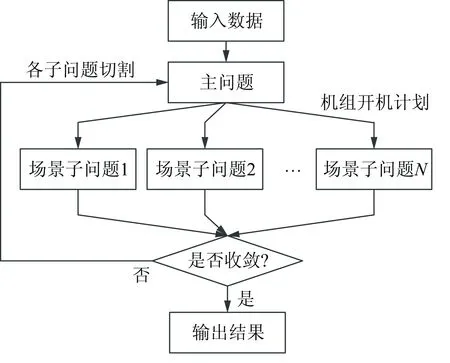
图2 求解算法框图

有利于减轻对内存的需求。另外，在实际计算中，借鉴文献[15]提出的方法，初步确定大容量机组的开机计划以识别模型中部分待求解的整数变量，可以减少分解算法的迭代次数。

2.3 新能源指标计算方法

周生产模拟数学模型求解结束后，该周新能源接纳电量为

(27)

该周新能源可利用电量为

(28)

由此，得到该周的弃电率：

ηw=(1-qaccept/qavailable)×100%

(29)

可由下式计算1个月的弃电率：

(30)

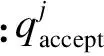
3 算例分析

考虑到本文研究的是生产模拟方法，故在给定电源结构后，分析一个典型年的生产模拟结果，而不讨论电源规划的最终方案。

3.1 算例介绍

本算例对西北地区某2省某规划年的电源规划方案进行生产模拟。之所以将2省统一进行电源规划，主要是因为发挥区域水、火、风、光各类型电源互济。算例仅考虑内用电源，即各类型电源均用以满足省内负荷需求，不考虑区域外送的影响。规划系统在规划年的年最大负荷为41 382 MW，负荷利用小时数为6 500 h。

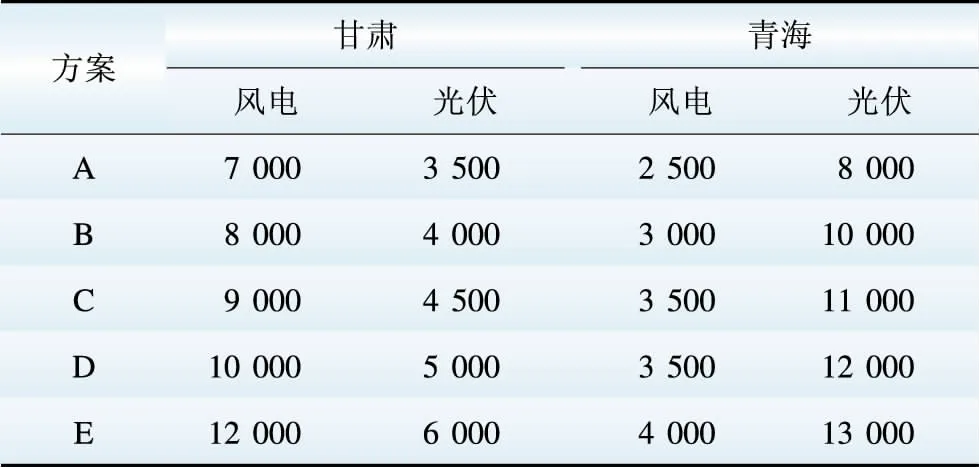
确定一个常规电源规划方案如表1所示。为研究不同新能源装机容量对生产模拟结果的影响，给出5个新能源规划方案进行比较，如表2所示。

收集省级风、光历史出力数据并分别建立省级风电、光伏出力模型。考虑到风电随机性较强，而光伏出力有着明显的日特性，形成各季节风电、光伏出力场景集后，利用k-均值聚类法[12]，将各季节风电、光伏场景分别聚类成6个和3个，则在周生产模拟中，有18个电力平衡场景。

表1 常规电源规划方案

Table 1 Conventional generation planning MW

表2 新能源规划方案

在生产模拟计算中做以下设定：(1)水电的可控性比风、光要好，故水电优先风、光接纳，而风、光不区分接纳顺序；(2)系统旋转备用率、冷备用率分别为当月最大用电负荷的8%和5%；(3)供热期所有供热机组都处于运行状态以保障供热；(4)提高失备用和失负荷成本，避免这些事件发生；(5)水电预想出力、平均出力采用平水年信息。下面以B方案，展示新能源接入后的生产模拟结果。

3.2 典型周分析

这里以春季为例，分析一个典型周的模拟结果。首先给出新能源弃电率最大场景下，各类型电源的带负荷面积，如图3所示。

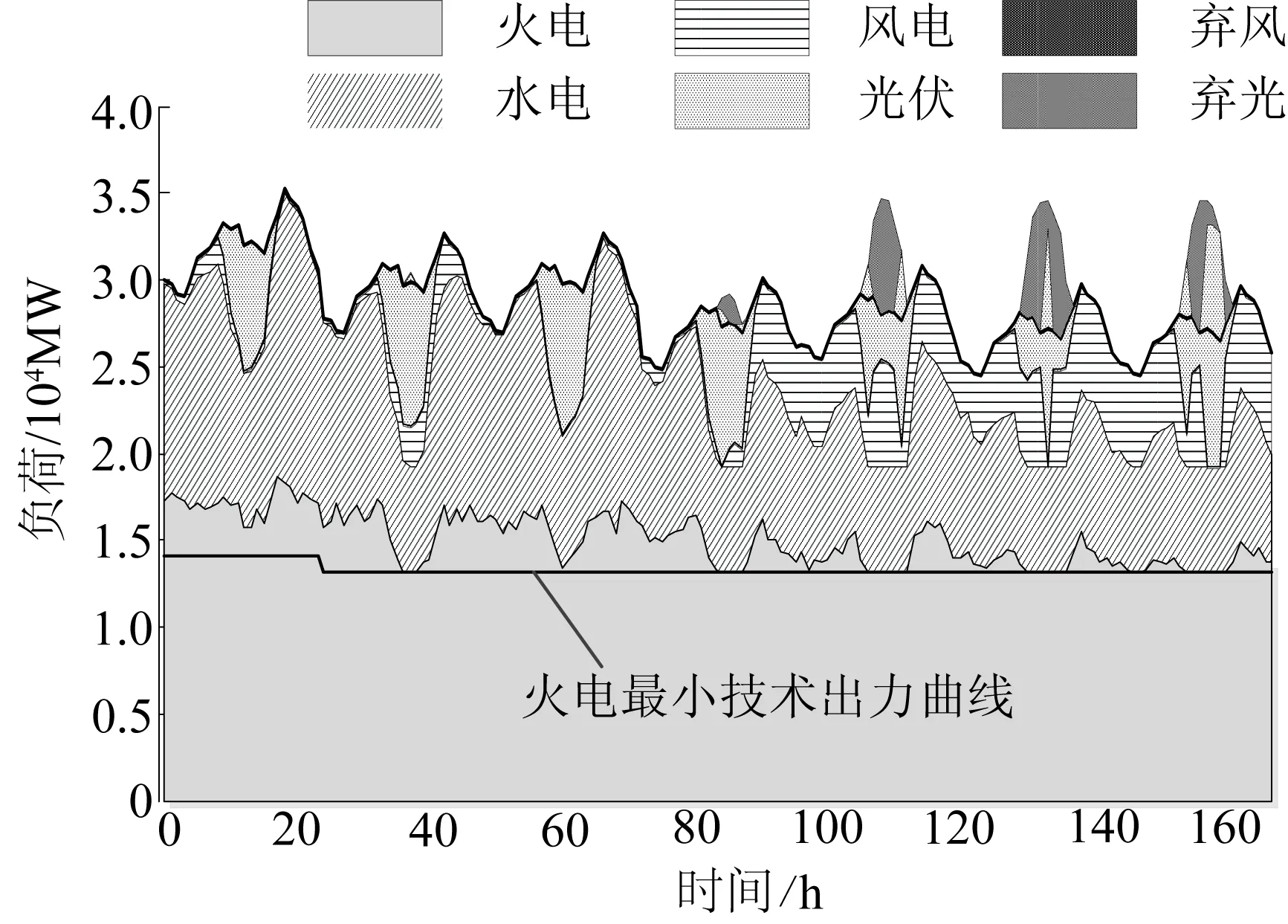
图3 某场景下各类型电源的带负荷面积

(1)该周负荷的整体趋势是周一负荷明显大于后6天，所以多运行了容量共计1 650 MW的火电，这些火电在本周第2天进入停机状态。火电提供了绝大部分旋转备用以应对负荷和新能源出力的不确定性。一方面，备用需求使得火电保持一个较大的开机方式；另一方面，火电开机数量偏多，不得不减少出力以接纳新能源。

(2)风、光大规模接入后，正午成为日调峰最困难的时刻，这时光伏的出力处于1天中最大的时刻，即使将水电和火电的出力压至最低，光伏都不一定能够完全接纳。如果这时风电也有出力，那么就有可能引起“风光之争”，系统运行人员就会面临弃风或者弃光的选择。

(3)有库容的水电站承担了为新能源调峰的重任。正午过后，光伏出力逐渐下降，到了晚负荷高峰时，光伏的出力基本上降为0。此时，水电依靠其良好的运行特性，增加出力以满足电力平衡。所以水电在白天尽量不发电以接纳新能源；在夜晚多发电以弥补新能源总出力的减少。可见，在区域内发挥多种能源互济，将有利于促进新能源接纳。

统计18个场景下的新能源弃电率，得到该周综合所有场景后的新能源弃电率概率密度和概率分布，如图4所示。由图4可知，弃电率主要分布在7%～10%，约占了场景数量的一半。弃电率≥13%的场景约占总场景数量的10%，因此，从概率分布的角度，有90%的可能该周弃电率小于13%。

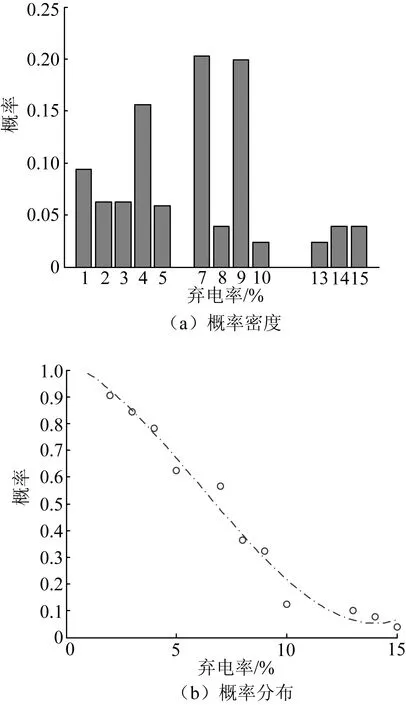
图4 典型周弃电率的概率信息

3.3 年指标汇总

对全年逐周进行生产模拟后，按式(30)计算各月的新能源弃电率，结果如图5所示。

由图5可知，1—3月和7—8月是全年新能源接纳比较困难的时期。1—3月处于西北地区的供热期，所有调峰能力有限的供热机组必须处于运行状态。因此，系统可控电源的调峰能力不足导致了这3个月弃电率较高。同样是处于供热期的11、12月份的新能源接纳问题并不突出，这是因为11、12月是全年负荷最大的月份，按照本文所提出的算法优化系统运行后，即使所有供热机组全部处于运行，仍然能够保证有足够的发电空间留给新能源和水电。7—8月是西北地区1年间的丰水期，在水电优先新能源接纳的前提下，水电大发直接导致新能源发电空间被压缩。

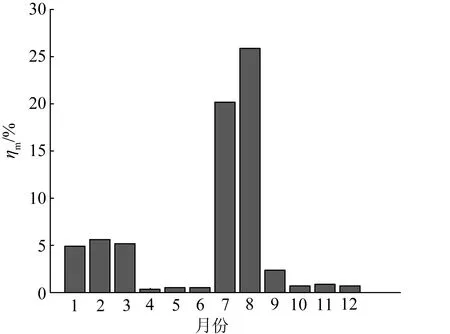
图5 各月新能源弃电率

表3是生产模拟后的年指标，火电盈余装机容量指的是在负荷最大月，考虑检修、冷备用等因素后，仍未开机的火电容量。1 723 MW的火电盈余装机容量可通过电源规划迭代予以削减。

表3 生产模拟的年指标

Table 3 Index of production simulation in a year

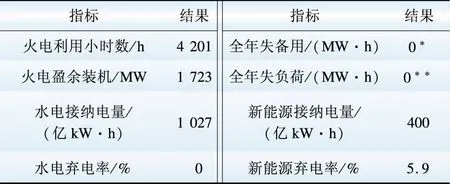
注：*、**表示由于装机不足而造成的失负荷、失备用。

3.4 场景数量和求解方法对生产模拟结果的影响

为体现本文所采用的解法相对于直接求解的优势，以新能源装机规模最大的方案E为例，比较了2种解法在不同场景数量下，生产模拟得到的新能源弃电率，结果如表4所示。计算平台为1台处理器为i7-4790k，4GHz，内存8G的PC。

首先，风电、光伏场景数量越少，弃电率越低。这是因为场景聚类后，一些高出力的风电场景被中等出力甚至低出力风电场景平均化，使风电接纳情况偏乐观。可是，场景数量过多也会增加模型求解难度，并且对计算结果影响不大。

表4 不同场景数量和求解方法下的生产模拟结果

Table 4 Production simulation results of different scenarios and solution methods

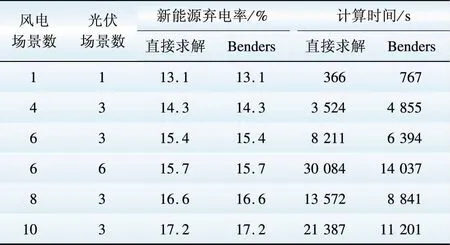
各场景下，直接求解和基于Benders分解的求解方法得到相同的新能源弃电率，验证了本文求解方法的理论正确性。在大部分场合下，本文算法的计算时间都优于直接求解，并且场景数量越多，越能得到体现。但在场景数量较少的情况下，由于benders法中迭代、串行求解场景子问题需要一定的时间，因此，直接求解更占优势。

3.5 旋转备用率对新能源弃电率、接纳电量的影响

降低旋转备用需求将减少火电开机数量，有利于新能源接纳。在实际运行中，可以通过联络线由省外电源提供旋转备用，在系统发生失负荷或失备用时，由外省购电的方式及时满足用电需求。所以，考虑省际功率交换后，系统的旋转备用率允许适当地降低。本节对比旋转备用率为2%、4%、6%、8%时，各新能源规划方案下的新能源弃电率、接纳电量，如图6、7所示。随着旋转备用率增加，所有方案的弃电率都单调增加，新能源接纳电量则逐渐减少。

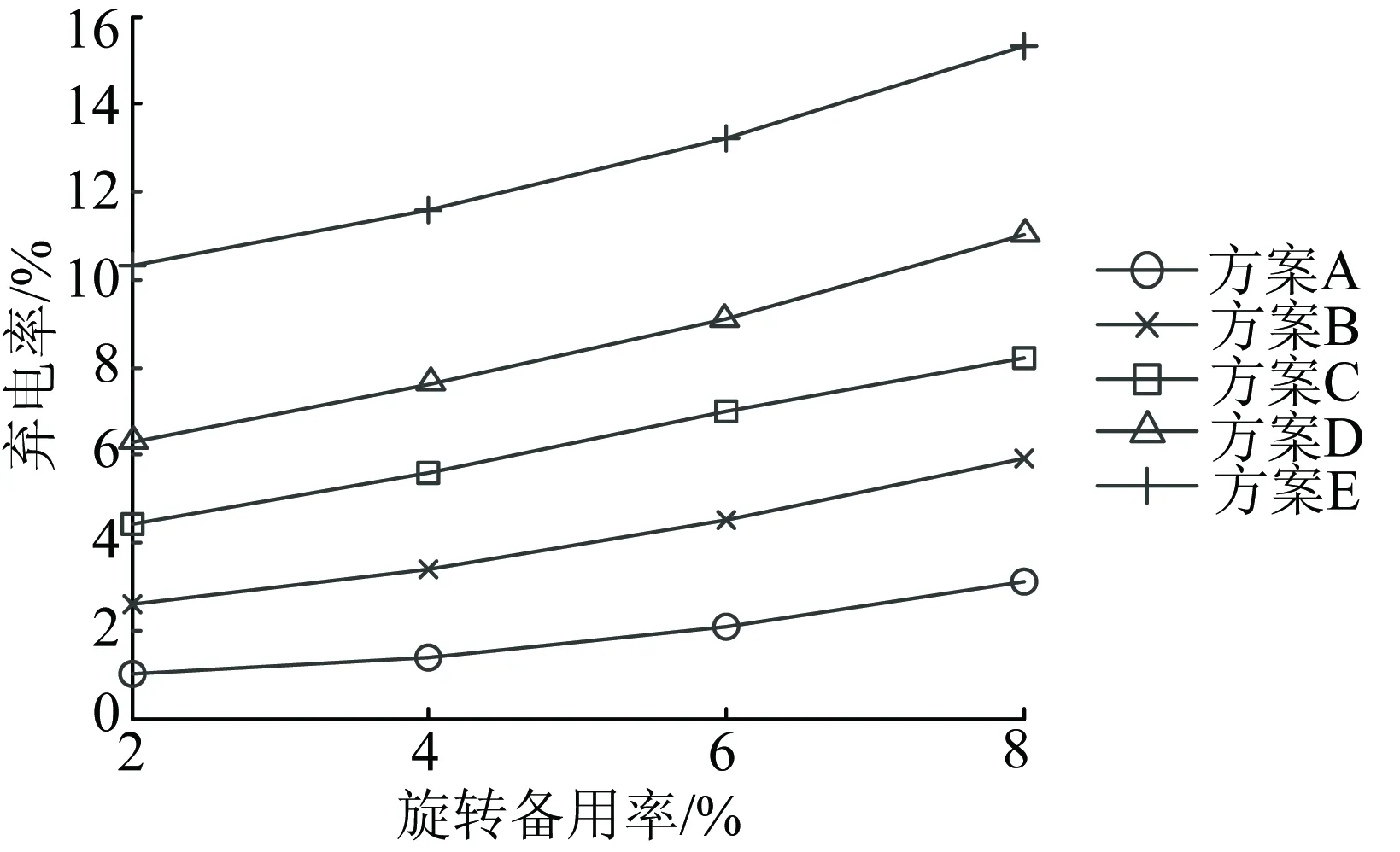
图6 不同旋转备用率下各方案的新能源弃电率

4 结 论

本文研究了含新能源的生产模拟方法，与先前研究相比，本文采用了多场景的方式对新能源建模，建立随机规划模型模拟系统运行，并通过基于Benders分解的算法求解。算例结果表明，本文所提生产模拟方法能够考虑新能源的不确定性，安排确定的开机计划；通过对计算结果分析，指出不同时间尺度下，系统新能源接纳能力不足的时段，并提供新能源弃电率、火电盈余装机容量等电源规划所关心的指标；在求解算法方面，本文所采用的方法相对于直接调用数学软件求解有一定的优势。

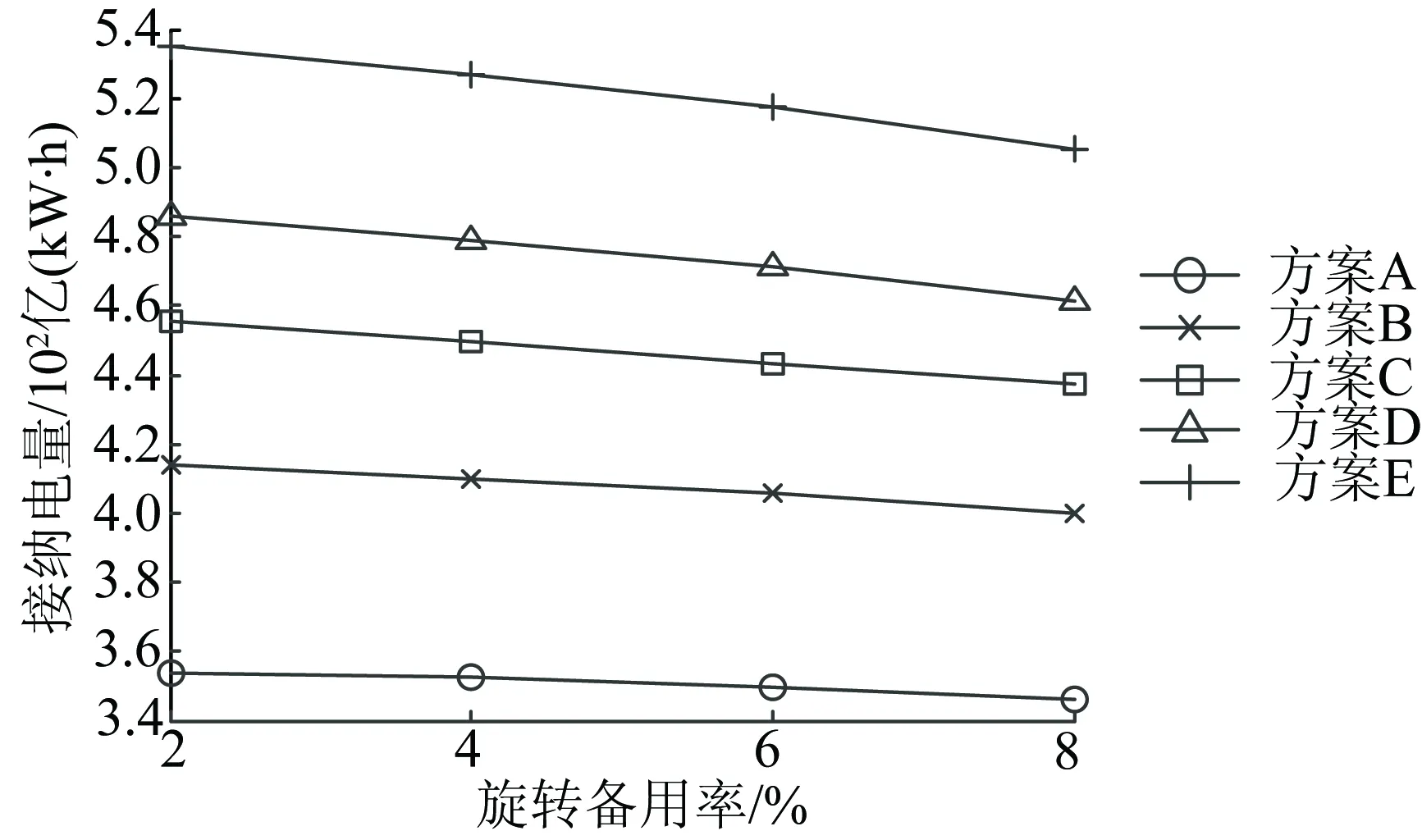
图7 不同旋转备用率下各方案的新能源接纳电量

[1]张谦, 王海潜, 谢珍建. 江苏电网消纳大规模风电的电源规划设计[J]. 电力系统自动化, 2011, 35(22): 60-65.

ZHANG Qian, WANG Haiqian, XIE Zhenjian. Generation expansion planning with large-scale wind power integration into Jiangsu power grid[J]. Automation of Electric Power Systems, 2011,35(22):60-65.

[2]吕泉，王伟，韩水，等． 基于调峰能力分析的电网弃风情况评估方法[J]．电网技术，2013，37(7)：1887-1894．

LV Quan， WANG Wei， HAN Shui， et al. A new evaluation method for wind power curtailment based on analysis of system reguation capability[J]．Power System Technology，2013，37(7)：1887-1894.

[3]刘德伟, 黄越辉, 王伟胜, 等. 考虑调峰和电网输送约束的省级系统风电消纳能力分析[J]. 电力系统自动化, 2011, 35(22): 77-81.

LIU Dewei, HUANG Yuehui, WANG Weisheng, et al. Analysis on provincial system available capability ofaccommodating wind power considering peak loaddispatch and transmission constraints[J]. Automation of Electric Power Systems, 2011, 35(22): 77-81.

[4]陈启鑫, 康重庆, 夏清, 等. 电力行业低碳化的关键要素分析及其对电源规划的影响[J]. 电力系统自动化, 2009, 33(15): 18-23.

CHEN Qixin, KANG Chongqing，XIA Qing，et al. Key low carbon factors in evolution of power decarbonization and their impacts on generation expansion planning[J], Automation ofElectric Power Systems, 2009, 33(15): 18-23.

[5]刘纯，曹阳，黄越辉，等．基于时序仿真的风电年度计划制定方法[J]．电力系统自动化，2014，38(11)：13-19．

LIU Chun，CAO Yang，HUANG Yuehui，et al．An annual wind power planning method based on time sequential simulations[J]．Automation of Electric Power System，2014，38(11)：13-19．

[6]王锡凡． 包含多个水电机组的电力系统随机生产模拟[J]． 西安交通大学学报，1985，19(4)：69-82．

WANG Xifan． Probabilistic simulation of multiple assigned-energy hydroelectric units[J]． Journal of Xi’an Jiaotong University， 1985，19(4)：69-82．

[7]MAISONNEUVE N, GROSS G. A production simulation tool for systems with integrated wind energy resources[J]. IEEE Transactions on Power Systems, 2011,26(4):2285-2292.

[8]BIE Z, ZOU X, WANG Z, et al. Studies on models and algorithms of the power system probabilistic production simulation integrated with wind farm[C]//IEEE Power & Energy Society General Meeting.Calgary, AB, Canada:IEEE, 2009: 1-7.

[9]张节潭，程浩忠，胡泽春，等．含风电场的电力系统随机生产模拟[J]．中国电机工程学报，2009，29(28)：34-39．

ZHANG Jietan，CHENG Haozhong，HU Zechun，et al．Power system probabilistic production simulaition including wind farms[J]． Proceedings of the CSEE，2009，29(28)：34-39.

[10]姚力，黄镔,王秀丽，等．考虑风火联合外送的互联系统随机生产模拟[J]．电网技术，2015，39(5)：1219-1225．

YAO Li， HUANG bin， WANG Xiuli, et, al．Probabilistic production simulation of interconnected system by considering the joint delivery of wind power and thermal power generation [J]．Power System Technology，2015，39(5)：1219-1225.

[11]郭旭阳，谢开贵，胡博，等．计入光伏发电的电力系统分时段随机生产模拟[J]．电网技术，2013，37(6)：1499-1505.

GUO Xuyang，XIE Kaigui，HU Bo，et al．A time-interval based probabilistic production simulation of power system withgrid-connected photovoltaic generation[J]．Power System Technology，2013，37(6)：1499-1505．

[13]孙晚华. ILOG CPLEX与铁道运输优化[M]. 北京：中国铁道出版社, 2014．

[14]陈宝林. 最优化理论与算法[M]. 北京：清华大学出版社, 2005:237-238.

[15]宫本辉, 姚力, 傅旭, 等. 基于等效负荷区间和随机生产模拟的新能源接纳能力快速计算方法[J]. 电力建设, 2016,37 (3): 24-30.

GONG Benhui, YAO Li, FU Xu, et al. A fast calculation method for accommodation capacity of renewable energy based on the equivalent load interval and probability production simulation[J]. ElectricPower Construction, 2016,37 (3): 24-30.

姚力 (1991)，男，博士研究生，主要研究方向为电力系统随机生产模拟；

王秀丽(1961)，女，博士，教授，博士生导师，主要研究方向为电力系统规划、电力市场、电力系统可靠性、电力系统分析、新型输电方式等;

肖汉(1975)，男，高级工程师，主要从事电力系统规划分析方面的工作；

傅旭(1976)，男，高级工程师，主要从事电力系统规划分析方面的工作；

李彬(1962)，男，教授级高级工程师，主要研究方向为电力系统规划和运行。

(编辑 张小飞)

Production Simulation Method of Power System Based on Multi-Scenario Stochastic Programming

YAO Li1, WANG Xiuli1, XIAO Han2,FU Xu3,LI Bin2, YANG Panfeng3

(1. School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2. Southwest Electric Power Design Institute Co., Ltd., Chengdu 61000, China; 3. Northwest Electric Power Design Institute Co., Ltd., Xi’an 710049, China)

According to the uncertainty problem of renewable energy in the production simulation of power system, this paper uses the theory of multi-scenario stochastic programming to study the production simulation method for the power system with renewable energy. For the weekly production simulation, the uncertainty of renewable energy is characterized by multiple scenarios, and the stochastic programming model is established to simulate the system operation, and solved by the algorithm based on Benders decomposition. With a case for real power system, we calculate indicators such as annual spillage rate of renewable energy and thermal power surplus installed capacity, compare the results solved by different methods, and study the impact of spinning reserve ratio on the accommodation capacity of renewable energy. The results show that the proposed method can calculate the index related to the system operation, the algorithm adopted has advantages compared with the approach that using mathematical software directly. In addition, this paper presents the relationship between the spinning reserve ratio and the spillage rate as well as the accommodate energy of renewable energy.

production simulation; stochastic programming; accommodation capacity of renewable energy

中国电力工程顾问集团科技项目(间歇性电源规划方法及计算模型研究)

TM 711

A

1000-7229(2016)12-0074-08

10.3969/j.issn.1000-7229.2016.12.010

2016-07-25