一道高考试题的背景与拓展

潘荣杰

(北京市第八十中学 100102)

几何问题中的定值问题其实就是研究几何图形在运动变化过程中的恒成立问题，这种恒成立问题反映了该几何问题的本质特征．因为定值问题是几何问题的核心问题之一，所以在全国各地高考试题中，对圆锥曲线中的定值问题考查屡见不鲜．下面就2016年北京文科高考19题的背景与拓展谈谈笔者的一点思考．

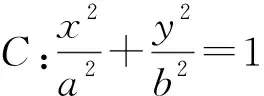
(Ⅰ)求椭圆C的方程及离心率；

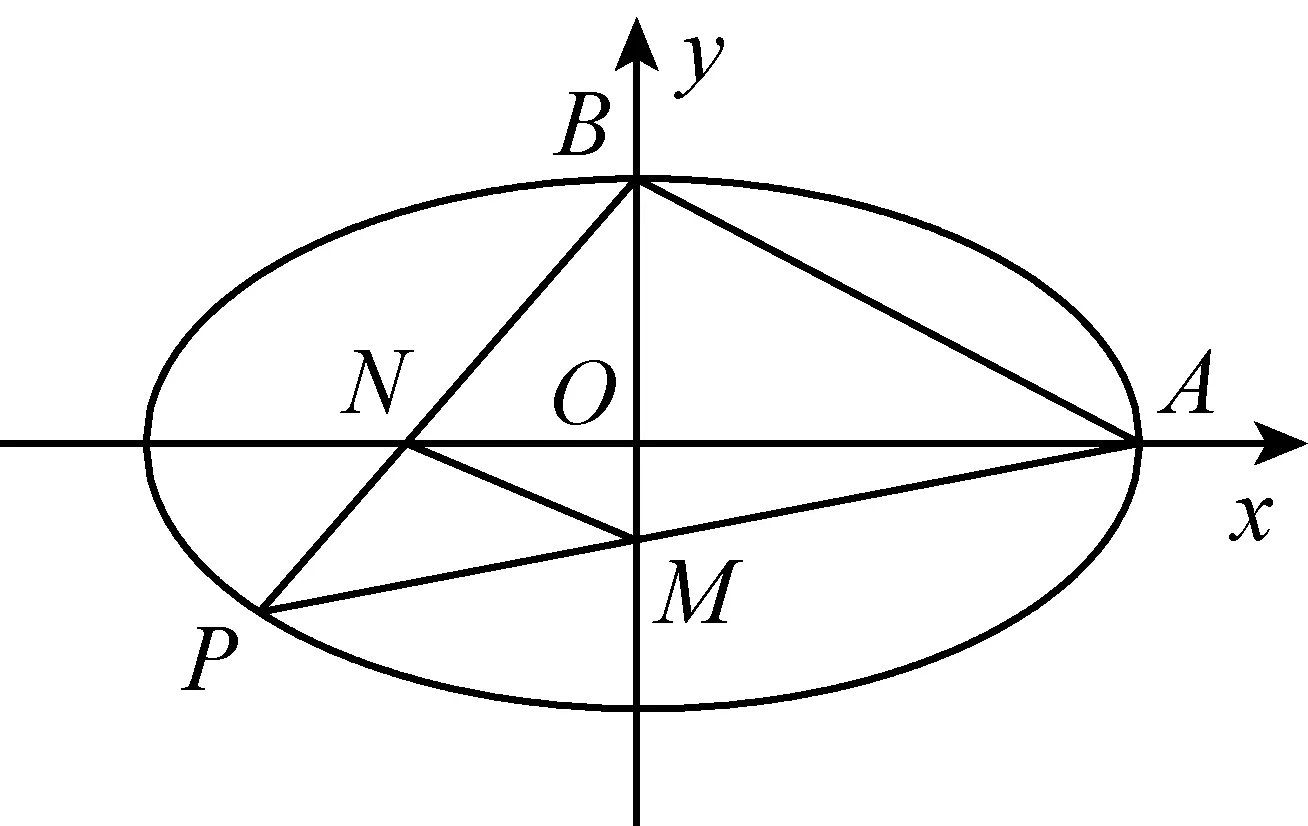
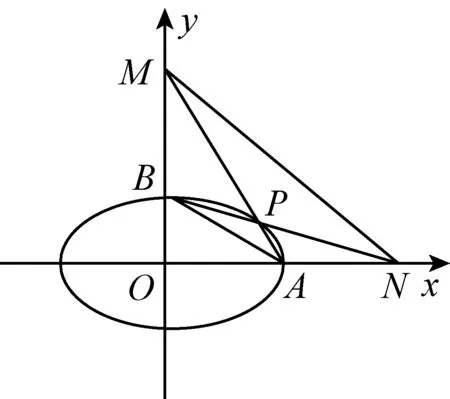
(Ⅱ)设P为第三象限内一点且在椭圆C上，直线PA与y轴交于点M，直线PB与x轴交于点N．求证：四边形ABNM的面积为定值．

【问题简析】第二问是一个定值问题，定值问题的本质是一种恒成立问题，解决定值问题的方法有两种，一种是引入参数，建立函数关系，化简求解；另一种是先猜后证，先特殊后一般．

【问题解答】(Ⅰ)由题意得，a=2，b=1．

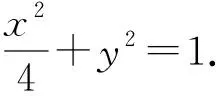
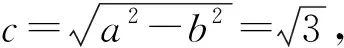
(Ⅱ)设P(x0,y0)(x0<0,y0<0)，

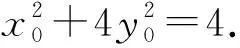
又A(2,0)，B(0,1)，

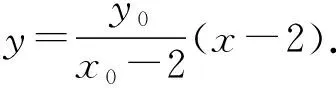
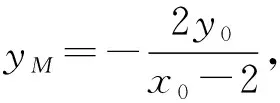
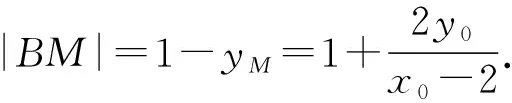
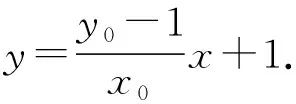
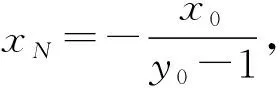
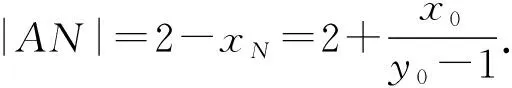
所以四边形ABNM的面积

从而四边形ABNM的面积为定值．

【方法点评】引入点P的坐标(x0,y0)，建立面积S与x0,y0的关系S=f(x0,y0)，化简f(x0,y0)求得定值．也可以引入直线PB的斜率k，建立S与k的关系S=f(k)，化简f(k)求得定值．

【追根溯源】为什么四边形ABNM的面积为定值？

设椭圆C在直角坐标系Oxy下的方程为：

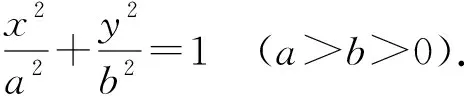
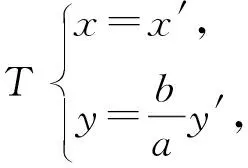
则椭圆C方程变为x′2+y′2=a2．

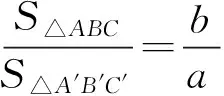
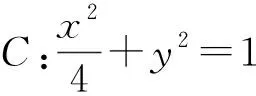
下面给出一种几何证明方法．

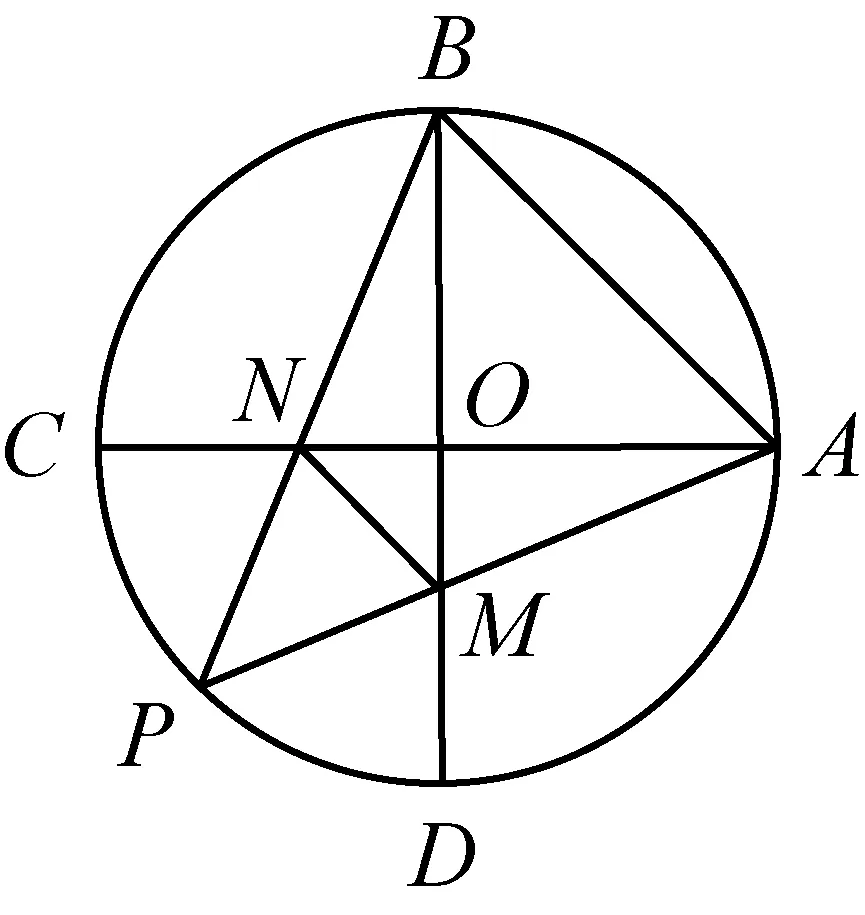
【推理证明】设∠PBM=α,∠PAN=β，

则α+β=45°

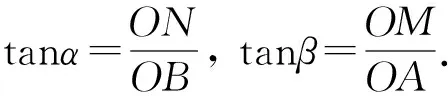
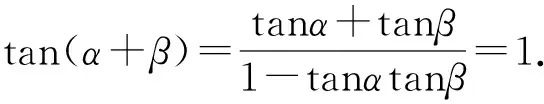
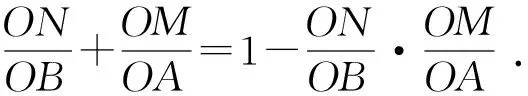
又OA=OB=R．即

OM·ON+ON·OB+OM·OA

=OA·OB=R2．

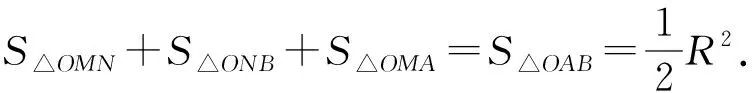
四边形ABNM的面积为

S△OMN+S△ONB+S△OMA+S△OAB=R2．

四边形ABNM的面积为定值R2．

根据仿射变换，我们很容易将圆中的一些性质推广到椭圆上去．

【拓展延伸1】椭圆上点P不在第三象限内时，是否还有类似的性质？比如P为第一象限内一点，类比猜想“谁”的面积为定值？

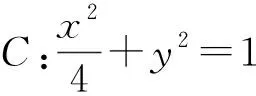
【尝试验证】设P(x0,y0)(x0>0,y0>0)，

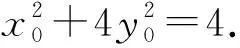
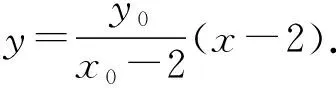
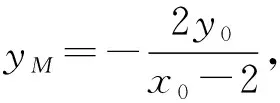
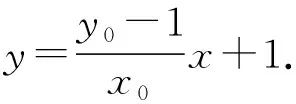
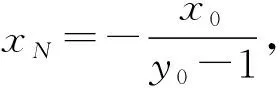
S△PMN-S△PAB=S△NBM-S△ABM

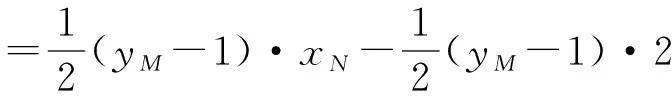
=2．

从而三角形PMN与三角形PAB的面积之差为定值．

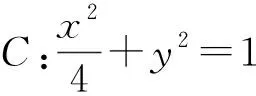
我们用同样的方法可以证明，这里不再赘述．

【知识铺垫】过椭圆中心的弦叫椭圆的直径．平行于直径CD的弦的中点的轨迹AB和直径CD互为共轭直径．当一对共轭直径互相垂直时，即为椭圆的长轴和短轴．

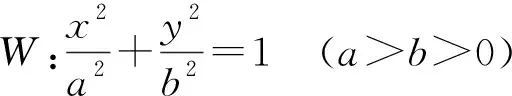
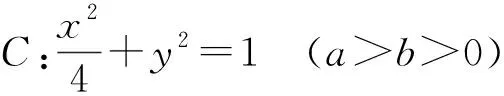
【尝试验证】如图，不妨设定点A(2cosθ,sinθ)，且点A在第一象限，B(2cosα,sinα)，且点B在第四象限．

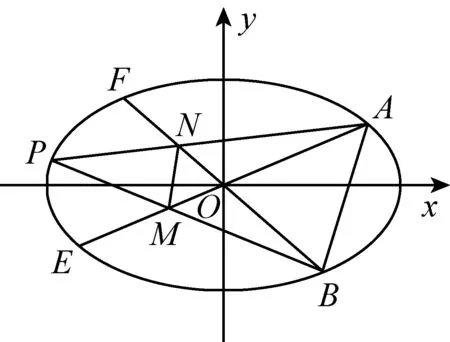
此时B(2sinθ,-cosθ)，设P(2cosβ,sinβ)，

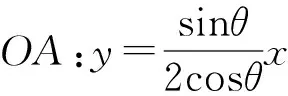
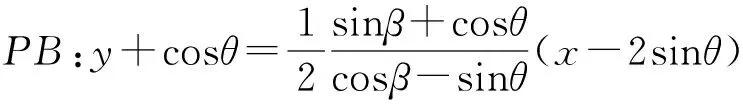
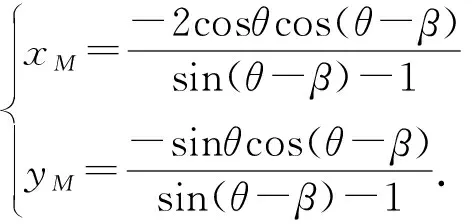
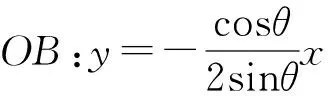
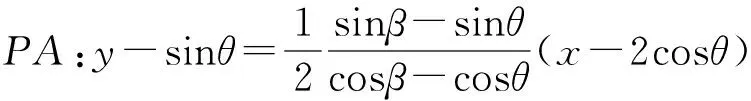
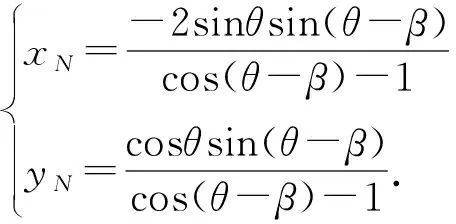
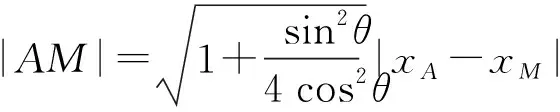
点N、点B到直线AE的距离分别为dN,dB．

四边形ABMN的面积为

=2(定值)．

成功！ 我们的猜想又是正确的．

对本题的探索也许刚刚开始，很多数学问题的解答也许并不困难，但若缺少了思考、追问、猜想、验证，数学学习者就很难抓住问题本质．问题是数学的心脏，如果能对核心问题深入探究，不断从一个特殊问题逐步引申到另一个一般性问题，这种自发的提出问题、解决问题的数学研究学习过程，一定会使得我们的数学学习更加有意义．