数学史视角下“数系的扩充和复数的概念”的教学思考①

王海青

(1. 广州大学数学与信息科学学院，510006；2. 广东省惠州市惠州学院数学系，516007)

数学概念是整个数学体系这座大厦的根基．只有根基稳了，大厦才牢靠．数学概念特别是基础的、核心的概念的产生，往往在数学发展的历史进程中起到重要的推动作用，甚至支撑着一门学科分支的发展．因此，概念教学历来在数学教学中具有不可撼动的地位．

数学学习是一个数学知识再发现的过程．数学概念学习也应使学生从中体验数学知识的形成过程，习得相应的数学思想方法．如弗赖登塔尔所言：“年轻的学习者重蹈人类的学习过程，尽管方式改变了．”[1]所以了解相关概念的历史有助于教师深刻理解概念并进行有效的教学设计．复数是数学学科中的核心概念，相应的教学内容也是教与学的难点．下面以“数系的扩充和复数的概念”为例，阐述如何利用数学史对教科书内容进行“再创造”，实现数学再发现的过程．

1 基于课程标准和教科书内容的教学目标分析

依照上面的思想，为了解决像方程x2+1=0在实数集内无解的问题，必须引入新数，因为“数不够用了”．同样，扩充后的运算要能和扩充前保持一致，不出现矛盾．由此给出了复数的代数形式及其几何意义．

根据以上教科书内容的安排，教学目标主要是让学生：(1)了解数系扩充的目的和原则，体会蕴含其中的数学思想；(2)明白为什么要引入虚数和规定i2=-1；(3)结合适当习题，理解复数的代数形式a+bi；(4)结合复数的几何解释，深化对复数概念的理解．

2 常见教学设计中复数概念的引入

数学概念的教学大致分为概念的引入、概念的理解和概念的运用三个阶段．[3,4]概念的引入是概念教学中最为重要也最难突破的环节，它极大地影响着学生对概念的理解和运用．有许多关于复数的教学建议和新颖的教学设计值得我们借鉴[5-7]．但在复数概念的引入环节笔者有些地方心存疑惑，在此提出与同行探讨．

疑惑1：关于问题情境的设置．

有些教学设计为了引入新数，在回顾自然数系扩充至实数系的过程中强调两条主线对数学发展的作用．由此从数学内部发展的需要创设了“卡丹问题”(即已知两数的和为10及这两数的积为40，求这两个数)或其变式的问题情境．

首先，在引入问题时既考虑两条主线的交替发展，又强调数系扩充的原则，这是否会削弱了情境的作用而影响学生对问题的把握？另外，从回顾数系的扩充看由“卡丹问题”引入虚数似乎在情理之中．但数系的前几次扩充都有一个共同点，即为解决实际问题的迫切需要而引入新数．从实数系向复数系扩充则找不到生活中的模型，这也恰是在引入复数的教学中学生难于接受和理解的地方．对学生而言，像方程x2+1=0是没有任何实际意义而不需加于考虑的．那为什么非要引入新数让它有解呢？

笔者以为，用“卡丹问题”来引入新概念，既不能有力回答“为什么要学”，又不符合数学历史的发展事实．在现实中容易找到两个数之和或之积为一定值，却未必能找到两个数同时满足这两个条件．历史上，复数的出现也不是为了解决一元二次方程而产生的．从古希腊的丟番图一直到16世纪前半叶，数学家们对类似方程x2+1=0的问题也都置之不理．

疑惑2:关于虚数的规定．

教科书引入新数i，并规定i2=-1．许多教师不加解释地将规定抛给学生．为什么要规定i2=-1，而不是i2=-2或其它？这看似细小的问题，却影响学生对虚数的理解和把握，需要在教学过程中给予清楚的说明．

3 复数的产生和发展历史

到底是什么使得数学家不得不引入虚数？回顾复数产生和发展的历史可以帮助我们更好地理解复数，体会数学家们在解决相关内容时所面临的困难．这也正是学生在相同问题的学习中将要碰到的困惑，即学生对某些数学概念的认知与概念的历史发展之间具有相似性[8]．事实上，复数的引入并非源于实际的问题背景，纯粹是解决数学内部问题的需要．

公元628年左右印度数学家婆罗摩笈多就给出负数的运算法则并指出负数没有平方根．之后的数学家在实际计算中出现负数的开平方时也是直接将其摒弃的．大约在1535年，意大利的数学家塔尔塔利亚宣布发现了三次方程的代数解法，并在多次的解三次方程比赛中获胜．意大利的另外一位数学家兼医生卡丹从塔尔塔利亚那里获得解三次方程的诀窍并发誓保守秘密．1545年，卡丹在他的《重要的艺术》里发表了形如x3+px+q=0的三次方程解法和其中一个根的表达式，即

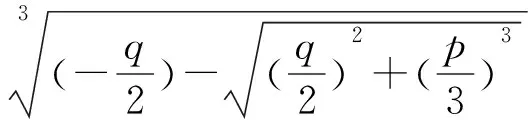
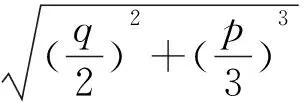
正是因为在解三次方程中出现了上述矛盾才使得数学家不得不去考虑实数与复数的联系，去研究复数的性质．但当时的许多大数学家(包括笛卡尔和牛顿)也对复数难于理解．如笛卡尔在他的《几何》中明确摒弃复根，认为这些根不是实的而是虚的，并把负数的开平方称作“虚数”[9]．对卡丹的三次方程解法的第一个完整的讨论是1732年由欧拉作出的，并给出了x3+px+q=0另外两个根的求根公式．

但即使是大数学家欧拉，在他得到著名的公式eix=cosx+isinx后，对于复数的理解也是不清晰的．1768年，欧拉在所著的《对代数的完整的介绍》中，认为：“……它们就其本性说来是不可能的数，因而通常叫作虚数或是幻想中的数，因为它们只存在于想象之中．”但他同时又认为它们是有用的．

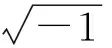
1837年，哈密顿将复数的逻辑建立在实数的基础上，使得复数的讨论依赖于实数．指出a+bi只不过是实数的有序偶(a,b)，并以此定义了复数纯形式的算术运算，也就是现在教科书中所介绍的复数的四则运算．

复数能用来表示平面上的向量，这就提供了表示向量及其运算的一个代数，能够通过复数代数地研究向量．而向量可以代表物理中的力、速度或加速度，因此复数的乘法可以解释为平面上物体运动的旋转和伸缩，这使得复数作为一个有用的工具立刻得到物理学家的认可．沿着这个方向哈密顿创造了四元数，间接推动了向量代数和向量分析的创立．复数及复函数方面的研究工作创造出单复变函数理论，这个数学分支统治了19世纪的数学．

复数的历史也表明，虽然复数的产生是为解决数学内部问题的需要，但它能得以繁荣发展却是因为后来人们发现它与物理学科有紧密联系，进一步地又推动了相关学科的发展．

4 复数概念的教学思考

教科书是知识的载体，而数学的思想与方法则蕴含在具体的知识中．数学教学的目的之一是通过对具体教学内容的学习使学生获得相应的数学思想方法．教科书基于编写的要求和简洁性的需要，不可能把知识的历史发展过程、蕴含的数学思想和如何组织教学都体现出来，否则就与大百科全书无异．因此，需要教师基于教科书、结合学生的实际对教学内容再组织和加工．

根据复数发展的历史，笔者尝试按以下线索展开教学(2个课时)：情境引入，集中凸显所学知识的重要性，解决学生学习的心理障碍→从概念的内涵和外延出发理解复数概念并对其精致化，扩充数系的结构→从复数概念的直观几何意义出发深化对概念的理解，体会数形结合的思想→回顾整个数系的扩充过程，明确扩充的目的和原则，理解数学知识产生和形成与现实需要的关系．

4.1 忠于历史设置数学问题情境，体会引入新知的需要

(1)回顾旧知，铺垫新知

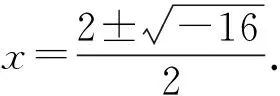
意图：为下一步讨论一元三次方程作铺垫，突出负数的平方根形式，形成对比．

(2)引入问题，凸显矛盾

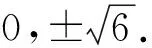
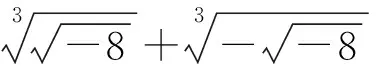
意图：让学生亲身体验到一个实数可以表示成带有负数的开平方的形式组合，以致人们不得不去考虑：负数的平方根具有怎样的性质？实数和这些曾经认为没有意义的根式到底存在怎样的联系？由此解除学生为什么要学习新知识的心理障碍，理解必须引入新数使得负数能进行开方运算以探讨它们的性质．

(3)引入新数，明确规定

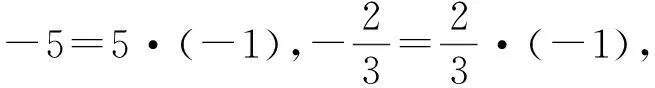
4.2 理解复数的代数形式a+bi并对其精致化

(1)从具体例子出发，理解概念的内涵

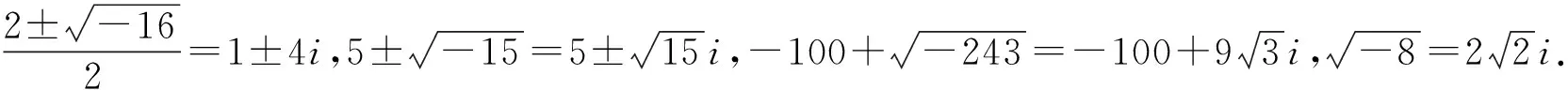
我们把形如z=a+bi(a,b∈R)的数叫做复数，全体复数所成的集合C={a+bi|a,b∈R}叫做复数集，a和b分别称为z的实部和虚部．

(2)从数学概念的二重性理解复数的代数形式a+bi

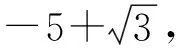
(3)对概念精致化，体现分类的思想

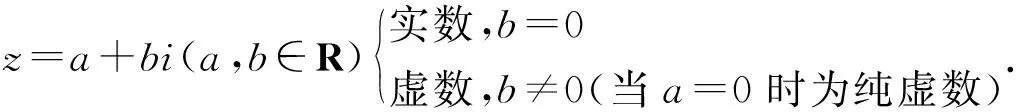
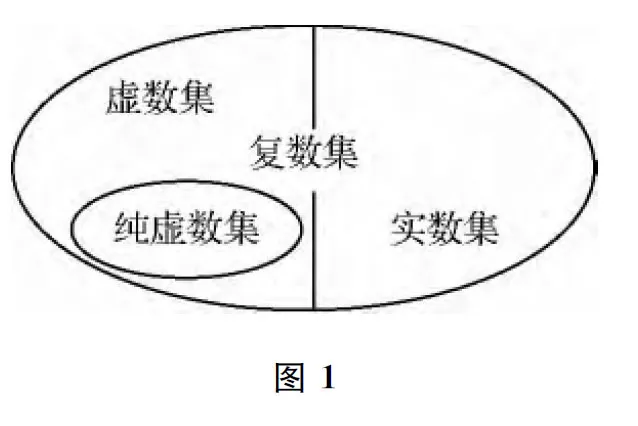
(4)概念的应用和巩固

给出两道简单的例题，从具体的复数形式对其进行分类和利用分类的条件确定具体的复数形式两个方面去理解巩固概念．

例2. 实数m取什么值时，复数z=m+1+(m-1)i是实数、虚数、纯虚数？

(5) 由有序实数对引出复数相等的充要条件

从复数的代数形式可以看出每个复数z=a+bi对应于一个有序实数对(a,b)，反过来每一个有序实数对(a,b)决定一个复数z=a+bi，即复数集与平面直角坐标系中的点集一一对应．因而在复数集中任取两个复数a+bi,c+di(a,b,c,d∈R)，我们自然地规定a+bi=c+di的充要条件是a=c,b=d．并让学生应用这个结论解答如下例题．

例3.已知(2x-1)+i=y-(3-y)i，其中x,y∈R，求x,y的值．

4.3 动静结合揭示复数的几何意义，深化对复数概念的直观理解

(1)从静态角度看复数的几何意义，帮助理解复数的性质

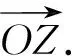
图2

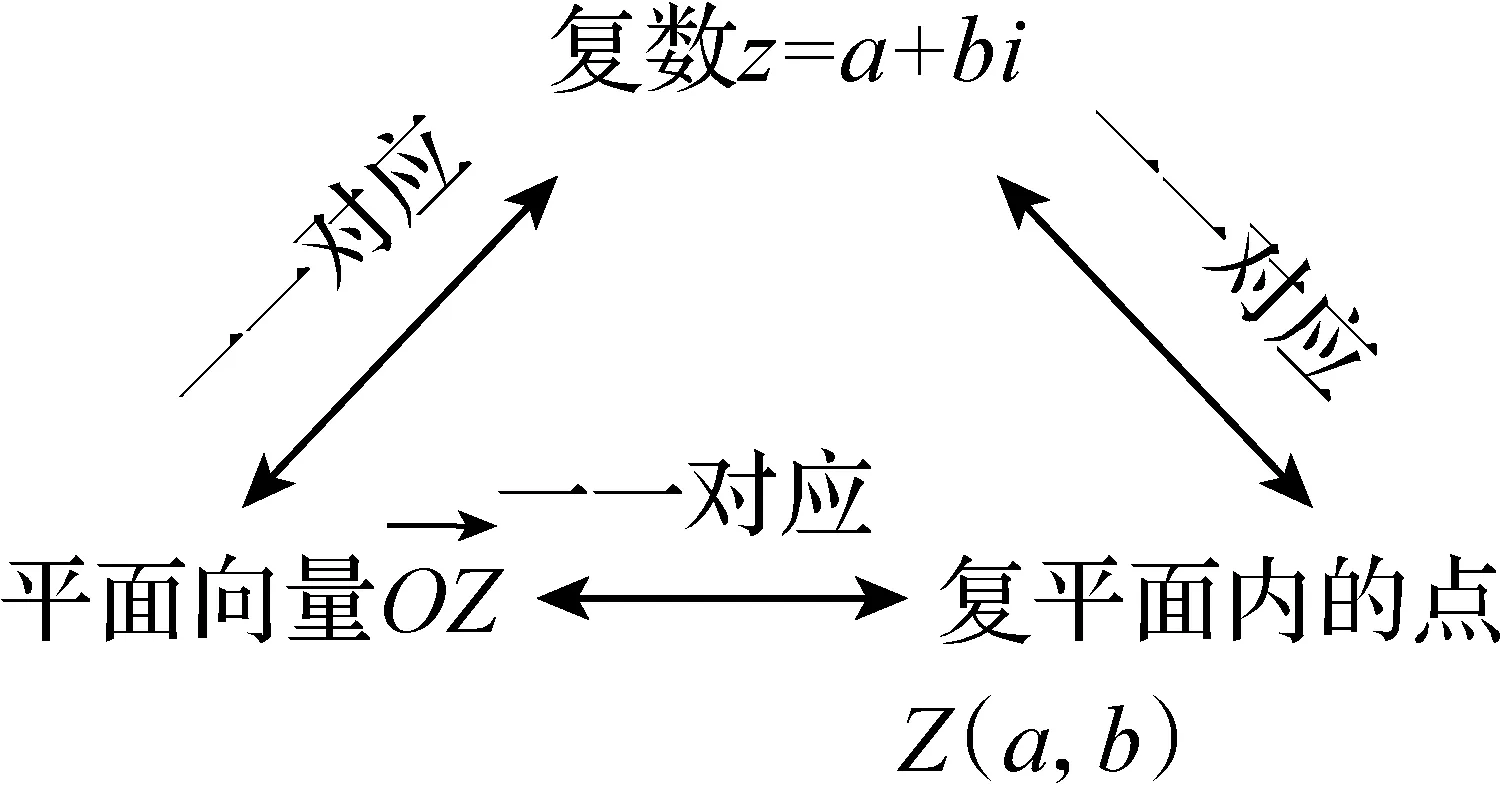
图3

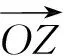
(2)从动态的观点看复数的几何意义，褪去i的神秘面纱

如图4，在数轴上， |OA|=1, |OB|=2， 1×(-1)=-1，2×(-1)=-2．用-1去乘1或2所得的结果就相当于将它们所对应的线段OA,OB绕着点O逆时针旋转1800而成，所以可把-1的作用看成是按逆时针方向转过1800的旋转．

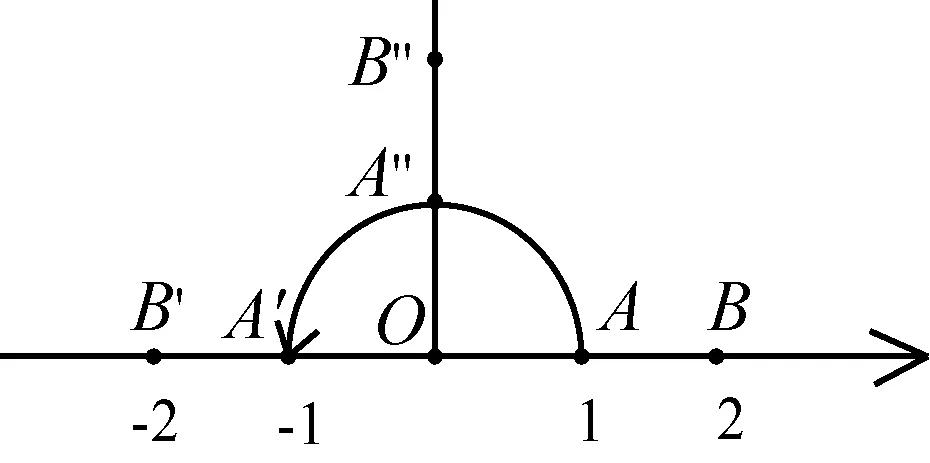
图4

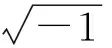
直观上看，被i作用一次的实数跑到实数轴外面去了，也就构成了一类新的虚数，数也就从一维的实数轴扩充到二维的复平面．

4.4 回顾数系的扩充过程，明确扩充的目的和原则

将数系扩充至复数后再回顾中小学阶段整个数系的扩充过程，有利于学生对数系发展的整体把握．在回顾的过程中，引导学生一起思考：每次扩充引入了什么数？解决了什么实际的和数学的问题？它们有什么共同的特点？也就是要明确扩充的目的和原则，体会到数学发展与数学内部需要特别是现实需要的重要联系．可通过如下表格比较扩充前后的运算情况和包含关系．

数系运算 自然数引入负整数→整数引入分数→有理数引入无理数→实数引入虚数→复数加法√√√√√乘法√√√√√乘方√√√√√减法×√√√√除法××√√√开奇数次方×××√√开偶数次方××××√自然数集N⊆整数集Z⊆有理数集Q⊆实数集R⊆复数集C