探求复合方程根的 分布问题基本策略
刘瑞美


为了研究问题的方便,我们规定:形如f[g(x)]=0的方程,称为复合方程,并将方程f(x)=0称为简单方程,其中x是未知数。
近年来,有关复合方程的根的问题经常出现在高考试题中,大部分考生遇到这样的问题往往情绪紧张,不知“路”在何方;也有的考生尽管基础很好,但由于分类不清和运算不当,使得思路受阻,影响到后续问题的解答。实际上解决此类问题的基本策略是分类讨论、数形结合以及换元法等数学思想方法的正确应用,进一步把复合方程转化成简单方程或者把方程根的问题转化成函数图像交点(函数零点)问题等。下面结合试题具体说一说策略的具体实施过程。
一、分类讨论须谨慎
运用分类讨论思想解决与复合方程有关问题时,要时刻注意分类的标准,一定要做到不重 复与不遗漏,这样才能得到正确的结果。
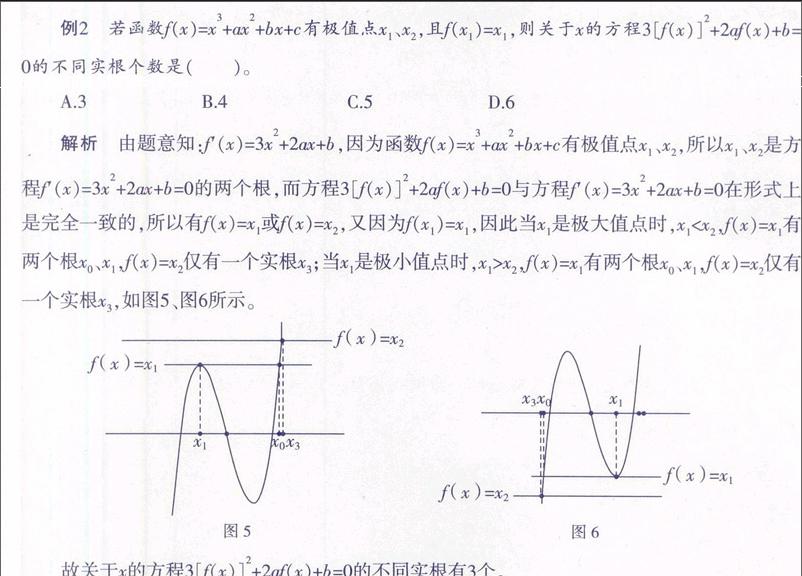
例1 已知函数f(x)=m·2+x+nx,若集合{x|f(x)=0}={x|f[f(x)]=0}≠?芰,则m+n的取值范围为( )。
A.(0,4)?摇 ?摇?摇?摇B.[0,4)?摇?摇?摇 ?摇C.(0,5]?摇 ?摇?摇?摇D.[0,5]
解析 令t=f(x),由{x|f(x)=0}={x|f[f(x)]=0}可得t=0时,f(t)=f(0)=m=0,因此f(x)=x+nx,则{x|f(x)=0}={0,-n},当f[f(x)]=0时,有f(x)=0或f(x)=-n,再由{x|f(x)=0}={x|f[f(x)]=0}≠?芰可知:f(x)=-n无解或f(x)=-n的解为0或-n,
(1)当f(x)=-n无解时,Δ=n-4n<0?圯0 (2)当f(x)=-n的解为0或-n时,n=0;于是由(1)、(2)可知:0≤n<4。 故m+n的取值范围是0≤n<4,因而选B。 点评 本题实际上考查的是与集合有关的问题。令集合A={x|f(x)=0},B={x|f[f(x)]=0},且满足A=B≠?芰,从而探求m+n的取值范围。 二、以形定数显神威 在解决有关复合方程问题时,分类讨论思想自然十分重要,但如果只考虑到分类,仅仅由数再到数,有时可能收效甚微,更有可能陷入无限循环的运算之中,运算量很大,最终导致思路受阻。如果能在分类的同时充分利用数形结合思想,就会使问题的解决变得直观和轻松。 例2 函数f(x)=ax+bx+c(a≠0)的图像关于直线x=-对称。据此可推测,对任意的非零实数a、b、c、m、n、p,关于x的方程m[f(x)]+nf(x)+p=0的解集都不可能是( )。 A.{1,2}?摇 ?摇?摇?摇?摇B.{1,4}?摇?摇?摇 ?摇C.{1,2,3,4}?摇 ?摇?摇D.{1,4,16,64} 解析 本题需要利用换元法,令t=f(x), 则原方程m[f(x)]+nf(x)+p=0 ①, 转化为一元二次方程mt+nt+p=0 ②, (1)分类清晰,思虑周密。 对于方程②,可以分以下三类: (ⅰ)方程②无实数解; (ⅱ)方程②有一个实数解,即有两个相等的实数解t; (ⅲ)方程②有两个不等的实数解t、t(不妨设t>t)。 (2)以形助数,方便直观。 著名数学家华罗庚说:“数缺形少直觉,形缺数难入微。数形结合百般好,隔离分家万事非。” 对于(ⅰ),易知①的实数解集为?芰; 对于(ⅱ),如图1及图2所示,由图1得到①的实数解集为{x,x},且x+x=-, 由图2得到①的实数解集为{x},且x=-; 对于(ⅲ),如图3及图4所示,由图3得到①的实数解集为{x,x,x,x}, 不妨设x 由图4得到①的实数解为{x,x,x},不妨设x 通过以上分析,可以对选项进行验证,1+64≠4+16,故选D。 点评 本题主要考查创新意识和数学应用的能力,是一道集方程与函数、数形结合、转化与归纳等思想于一体的难得的好题。命题立意没有刻意追求新、奇、特,虽是意料之外,却又在情理之中,它无“法”可依,无“型”可套,让试图利用题海战术“以量取胜”的幻想破灭。同时,该题要求我们在今后的学习中要努力揭示问题的数学本质,感悟数学思想方法,提高学习能力,提升数学素养,实现“以质取胜”。 例2 若函数f(x)=x+ax+bx+c有极值点x、x,且f(x)=x,则关于x的方程3[f(x)]+2af(x)+b=0的不同实根个数是( )。 A.3 ?摇?摇?摇?摇B.4 ?摇?摇?摇?摇?摇C.5 ?摇?摇?摇?摇D.6 解析 由题意知:f′(x)=3x+2ax+b,因为函数f(x)=x+ax+bx+c有极值点x、x,所以x、x是方程f′(x)=3x+2ax+b=0的两个根,而方程3[f(x)]+2af(x)+b=0与方程f′(x)=3x+2ax+b=0在形式上是完全一致的,所以有f(x)=x或f(x)=x,又因为f(x)=x,因此当x是极大值点时,x 故关于x的方程3[f(x)]+2af(x)+b=0的不同实根有3个。 点评 本题实际上是函数不动点的问题和方程根的问题,主要考查函数的极值和方程的根,需要考生具有极强的运算能力。 三、换元方法巧设置 在解决有关复合方程问题时,换元法是非常常用的,在换元过程中要时刻注意换元之后中间变量取值范围的变化,稍有不慎将会导致解答错误。利用这种方法将复合方程问题转化成简单方程或者转化成两个函数图像交点个数的问题,使得问题答案尽显图中,使问题的解决呈现直观性。 例3 设函数f(x)=,若关于x的方程[f(x)]-a|f(x)|+2=0有两个不相等的实数根,求实数a的取值范围。 解析 f(x)===1-∈(-1,1),且函数是单调递增的奇函数,其图像如图7所示,若关于x的方程[f(x)]-a|f(x)|+2=0有两个不相等的实数根,也即方程a=有两个不相等的实数根,令f(x)=t∈(-1,1),则即方程a=(-1 点评 复合方程求解常借助于换元法。涉及解的个数的问题,可将复合方程解的个数问题转化成方程组解的个数问题,再进一步将方程组解的个数问题转化成两函数图像交点的个数问题,实现由数到形,再由形到数的转化。 通过以上几道例题的探究我们可以发现,解决这类问题的共同方法:若方程f(x)=0的根分别为x,x,…,x,则对于复合方程f[f(x)]=0的根,就可以转化为研究方程f(x)=x,f(x)=x,…,f(x)=x根的讨论问题,这样就将复合方程问题转化成简单方程问题,又可以更进一步将方程根的问题转化为函数图像交点问题,然后利用数形结合使答案跃然纸上。
青苹果·高一版2016年4期
