一类三次函数恒成立问题的探究—由两道相似的高考题所想到的

江苏省江浦高级中学(211800)肖浩春

一类三次函数恒成立问题的探究—由两道相似的高考题所想到的

江苏省江浦高级中学(211800)肖浩春

在函数与导数的综合题中,可以说三次函数是最为常见和最为基本的函数之一.有关三次函数的问题,诸如极值、最值问题,单调性问题,函数零点问题,恒成立问题等等,一直是近几年高考的热点.本文笔者从两道相似的高考题中找出问题的不同,分析产生的原因,给出解决的办法.

三次函数 恒成立 图像

近日笔者在整理各省近几年高考题的时候,看到了这样两道题:

1.(2008江苏第14题)已知f(x)=ax3−3x+1≥0,对任意的x∈[−1,1],f(x)≥0都恒成立,则实数a的值为___.

2.(2014辽宁理第11题文第12题)对任意的x∈[−2,1],ax3−x2+4x+3≥0都成立,则实数a的取值范围为____.

一、求解方法和经历:

下面笔者用分离变量法来研究这两题:

1.解:因为ax3−3x+1≥0,所以ax3≥3x−1,当x=0时,不等式显然成立;并且

当x=0时,不等式显然成立,当x∈(0,1]时,

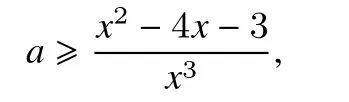
不难判断g(x)在x∈(0,1]上的最大值为g(1)=−6,在x∈[−2,0)上的最小值为g(−1)=−2,所以实数a的取值范围为−6≤a≤−2.

二、问题产生和解决:

这两题题设的条件是一样的,但是问题的结果却不一样,第1题是求值,答案是4,第2题是求范围,答案是[−6,−2],为什么会出现这种情况?

实际上刚才笔者在两题解答的过程中都提到了这样一个式子:m≤a≤n,只要m=n,则实数a的值只有一个,若m＜n,则实数a的值就不止一个了,有无数多个.若m＞n,则实数a的值不存在.而第1题出现了m=n,第2题出现了m＜n,所以问题就不难理解了.

三、问题拓展和探究:

那么知道了前面两个问题的解决方法和解决原理之后,我们不禁要问:什么时候问题的解只有一个呢?能找出更加广泛的情形吗?下面不妨再来研究这两道高考题的变式:

3.已知f(x)=ax3−3x+1≥0,对任意的x∈[p,q],f(x)≥0都恒成立,p,q满足什么条件,实数a的值有且只有一个?

思考:若p≥0或q≤0,通过分离变量法不难得到实数a的值不可能只有一个,结果是[m,+∞)或(−∞,n]的形式.所以p＜0,q＞0.因为ax3−3x+1≥0,所以

当x=0时,不等式显然成立,当x∈(0,q]时,

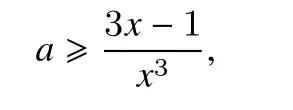
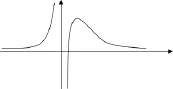
图1

结合图像分析:

4.对任意的x∈[p,q],ax3−x2+4x+3≥0都成立,p,q满足什么条件,实数a的值有且只有一个?

思考:同第3题不难分析出p＜0,q＞0因为ax3−x2+4x+3≥0,所以

当x=0时,不等式显然成立,当x∈(0,q]时,

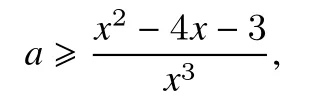
图2

反思:通过改编,我们不难发现能够使实数a的值只有一个的定义域是不惟一的,并且我们发现第4题的结果比第3题的结果还要复杂.究其原因,第3题只有一个极值(极大值),而第4题有两个极值(一个极大值和一个极小值),所以第4题的情况稍微复杂一些.

第3题研究的函数是只有一个极大值且极大值点为正值的情况,那么对于只有一个极值,若极大值点为负值和极值为极小值的这些情况,有兴趣的读者不妨研究下面两题:

案例1:对任意的x∈[p,q](p＜0,q＞0),ax3+3x+1≥0都成立,p,q满足什么条件,实数a的值有且只有一个?

案例2:对任意的x∈[p,q](p＜0,q＞0),ax3+cx+d≥0 (c,d都为常数)都成立,p,q满足什么条件,实数a的值有且只有一个?

对于案例2,笔者在这里做一下说明:由于x=0要满足不等式,所以d≥0,若d=0,则不等式提取公因式x之后可以转化为一元二次不等式,在这里笔者就不做研究了,所以不妨设d＞0.此时,若c=0,问题变得很简单,在这里笔者也不做研究了,所以c≠0.对于c＜0,d＞0这种情况,可以参考第3题进行分析;对于c＞0,d＞0这种情况,可以参考案例1进行分析.研究后不难发现极大值点为负值和极小值点为正值的情况是不存在的,只有极大值点为正值和极小值点为负值是存在的.

第4题研究的函数是两个极值点且极值点为一正一负的情况,那么对于有两个极值点,若极值点同正或同负的这些情况,有兴趣的读者不妨研究下面几题:

案例3:对任意的x∈[p,q](p＜0,q＞0),ax3+x2−2x+ 1≥0都成立,p,q满足什么条件,实数a的值有且只有一个?

二要积极争取中央和省市补助资金，充分发挥政府及有关部门的职能作用，吃透上级政策，加强沟通协调，积极提报水利重点项目，做好项目前期工作，用优良的投入收益率和先进的项目理念，争取国家的项目投资和上级的政策支持。

案例4:对任意的x∈[p,q](p＜0,q＞0),ax3+3x2−5x+1≥0都成立,p,q满足什么条件,实数a的值有且只有一个?

上述两个案例有一共同点:都是有两个极值点,且两个极值点都为正值.但是案例3却不存在p,q使得实数a的值有且只有一个,案例4是存在的.想一想,这是为什么?

案例5:对任意的x∈[p,q](p＜0,q＞0),ax3+x2+ 2x+1≥0都成立,p,q满足什么条件,实数a的值有且只有一个?

此案例有两个极值点,且两个极值点都为负值.

案例6:对任意的x∈[p,q](p＜0,q＞0),ax3+bx2+ cx+d≥0(b,c,d都是常数)都成立,p,q满足什么条件,实数a的值有且只有一个?

下面笔者对案例5做一下说明:

事实上不难看出b≠0,d＞0(若b=0,则不等式就转化为案例2;d＞0的理由同案例2)当x=0时,不等式成立,当x∈(0,q]时,

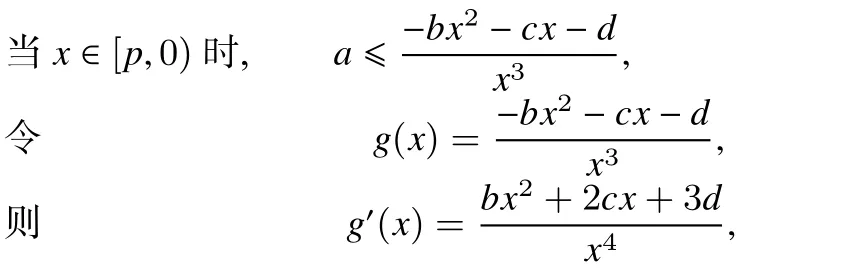
令bx2+2cx+3d=0,然后对b的正负及方程根的分布进行分析.

四、问题追击和归纳

前面我们研究了函数只有一个极值点和有两个极值点的情形,下面我们进一步探讨函数可能出现的其它一些情况.实际上上述案例5中令bx2+2cx+3d=0(b≠0,d＞0)时,我们就不难发现这是一个一元二次方程,所以根的情况有三种:无实数根,两个相等的实数根,两个不等的实数根.不难理解两个不等的实数根对应了有两个极值点的情况,而对于无实数根和两个相等的实数根则对应了无极值点的情况.

下面笔者对函数无极值点的情况进行说明:

案例7:对任意的x∈[p,q](p＜0,q＞0),ax3+x2−3x+ 3≥0都成立,p,q满足什么条件,实数a的值有且只有一个?

分析:因为ax3+x2−3x+3≥0,所以

所以g(x)在(−∞,0)和(0,+∞)上都为增函数,g(x)无极值点.下面我们结合g(x)(x∈(−∞,0)∪(0,+∞))的图像来研究实数a的值有没有可能有且只有一个.

图3

我们不难发现:

当x∈[p,0)时,a≤g(p),当x∈(0,q]时,a≥g(q)而g(p)＞0,g(q)＜0,所以无论p,q取何值,实数a的值都不可能有且只有一个.通过前面一系列的探究之后,让我们对这样的问题:“对任意的x∈[p,q](p＜0,q＞0),ax3+bx2+cx+d≥0(b,c,d都是常数)都成立,p,q满足什么条件,实数a的值有且只有一个?”有了一个初步的认识,这同时也让我们对部分分式函数的图像有了进一步理解.有了导数这个工具,很多较为复杂的函数(例如高次函数、分式函数、无理函数等等)的图像和性质问题都不难解决.

最后,笔者留给读者一个思考的空间:

思考1:对任意的x∈[p,q](p＜0,q＞0),ax3+bx2+ cx+d≥0(a,c,d都是常数,a≠0,c≠0,d＞0)都成立,实数b的值有没有可能有且只有一个?

思考2:对任意的x∈[p,q](p＜0,q＞0),ax3+bx2+ cx+d≥0(a,b,d都是常数,a≠0,b≠0,d＞0)都成立,实数c的值有没有可能有且只有一个?

思考3:对任意的x∈[p,q](p＜0,q＞0),ax3+bx2+ cx+d≥0(a,b,c都是常数,a≠0,b≠0,c≠0)都成立,实数d的值有没有可能有且只有一个?

每年的高考试卷中有一些看似平常的题,而实际上“暗藏杀机”,有很多考题值得去研究、去探讨、去反思.只有这样,我们才能提高自己的业务能力和教学水平,才能更好的服务学生,把握高考的方向.