采用互补信息熵的分类器集成差异性度量方法

赵军阳,韩崇昭,韩德强,张春霞

(1.第二炮兵工程大学202教研室, 710025, 西安;2.西安交通大学电子与信息工程学院, 710049, 西安;3.西安交通大学数学与统计学院, 710049, 西安)



采用互补信息熵的分类器集成差异性度量方法

赵军阳1,2,韩崇昭2,韩德强2,张春霞3

(1.第二炮兵工程大学202教研室, 710025, 西安;2.西安交通大学电子与信息工程学院, 710049, 西安;3.西安交通大学数学与统计学院, 710049, 西安)

针对多分类器系统差异性评价中无法直接处理模糊数据的问题,提出了一种采用互补信息熵的分类器集成差异性度量(CIE)方法。首先利用训练数据生成一系列基分类器,并对测试数据进行分类,将分类结果依次组合生成分类数据空间;然后采用模糊关系条件下的互补信息熵度量分类数据空间蕴含的不确定信息量,据此信息量判断基分类器间的差异性;最后以加入基分类器后数据空间差异性增加为选择分类器的基本准则,构建集成分类器系统,用于验证CIE差异性度量与集成分类精度之间的关系。实验结果表明,与Q统计方法相比,利用CIE方法进行分类器集成,平均集成分类精度提高了2.03%,分类器系统集成规模降低约17%,而且提高了集成系统处理多样化数据的能力。

分类器集成;差异性;互补信息熵;模糊关系

分类器集成是指针对某一问题,将一系列基分类器进行组合,来提高分类的精度和泛化性能的方法。目前,多分类器集成已得到广泛而深入的研究,并成为机器学习、模式识别等领域的主要研究方向之一。很显然,如果进行组合的是相同且无差异的分类器,集成系统并不能提高整体分类效果。因此,要提高多分类器系统的性能,基分类器必须具有一定的差异性,即要求B分类器能将A分类器错误分类的样本重新划分到正确的类别。

分类器差异性的研究主要涉及分类器差异性生成模式、差异性度量方法、差异性与集成分类性能关系以及如何利用差异性度量优化分类器集成系统等方面的研究[1-2]。其中,分类器差异性生成模式的研究是提高集成系统性能的基础[3],也是众多文献的研究热点。差异性的获得可通过采用不同类型的分类器、设置分类器的不同参数配置和采用不同的训练数据集来实现[4]。如何度量分类器间的差异性是研究者需要关注的另一个重要问题。分类器差异性的正确度量和分析对于设计性能优良的分类器系统至关重要。目前,国内外学者已经提出一些度量分类器差异性的方法,以期对分类器系统差异特性进行统计分析[5-9],如Kuncheva总结的Q统计、双错度量和熵度量等[5],Windeatt提出的基于模式的度量方法[6];或者指导分类器集成系统的优化设计与实现[10-14],以提高分类器的集成性能。现有的一些方法虽然能在一定程度上表示分类器之间的差异性,但主要是从分类器正确分类和错误分类的一致性角度出发进行定义,必须根据标准类别信息首先对分类器输出结果的正确性进行判别,无法直接度量分类器本身蕴含的分类信息。为此本文从信息熵角度出发研究如何直接度量分类器的差异性,提出一种基于互补信息熵的分类器差异性度量(CIE)方法,根据不同分类器所蕴含不确定信息量的差别来实现分类器的差异性评价,并分析差异性度量方法与系统集成性能之间的联系。数据实验表明,本文方法能有效度量分类器差异性,在降低分类器集成规模的同时,提高或保持集成系统的集成分类精度。

1 常用的差异性度量方法

目前比较常用的差异性度量方法主要可以分为两类:成对度量方法[5]和非成对度量方法[15]。

1.1 成对度量方法

成对差异度量方法首先计算分类器系统中每一对分类器之间的差异性度量值,L个分类器对应L(L-1)/2对差异值,然后对各差异值求取平均值得到系统的差异度。以下介绍几种常见的成对度量方法。

(1)相关系数(Correlation Coefficient,ρ)

ρi,j=(N11N00-N01N10)/[((N11+N10)(N01+

N00)(N11+N01)(N10+N00))1/2]

(1)

式中:N01表示分类器Di和Dj的联合分类输出概率,0表示Di分类错误,1表示Di分类正确;其余定义类似。

(2)Q统计(Q-statistic,Q)

(2)

(3)不一致度量(Disagreement Measure,Dis)

(3)

(4)双错度量(Double-Fault Measure,DDF)

(4)

1.2 非成对度量方法

非成对差异性度量方法不强调分类器两两之间的关系,而是对整个分类器集合进行计算得到系统的差异度。

(1)熵度量(Entropy,E)

(5)

式中:l(xi)表示在一组L个分类器中,将样本xi正确分类的分类器个数;N为样本数。

(2)KW方差(Kohavi-Wolpert variance,DKW)

(6)

(3)Kappa度量(Interrater agreement,κ)

(7)

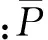
(4)难点度量(Difficulty,θ)

θ=var(Z)

(8)

式中:Z表示对于随机给定的输入x,分类正确的分类器在所有集成分类器中的比率。

(5)广义差异性度量(Generalised Diversity,DG)

(9)

式中:p(1)表示1个分类器的出错概率;p(2)表示2个分类器的出错概率。

(6)一致错误差异性度量(Coincident Failure Diveristy,DCF)

(10)

式中:p0表示所有个体部分类正确;pi表示L个分类器中有i个得出错误分类结果的概率。

2 互补信息熵差异性度量与集成

2.1 模糊近似空间中的互补信息熵

为了度量数据空间蕴含的不确定信息,目前已提出多种信息熵度量方法,但无论是Shannon信息熵[16]还是梁吉业提出的粗糙集中的信息熵模型[17]均要求数据空间满足一定的等价关系,只能处理离散数据。然而,实际的数据未必存在明确的边界区分,需利用连续特征函数进行描述,通过模糊隶属函数进行处理。为了适应任意模糊关系下的信息度量,文献[18]对Shannon熵进行改进,提出了模糊关系下的信息熵模型;作者则在文献[19]中考虑类别划分的补集,提出了任意模糊关系下的互补信息熵模型,可以直接处理连续或模糊数据。

定义1 设U={x1,x2,…,xn}为有限非空论域,R是U上的任意模糊关系,则模糊近似空间(U,R)的互补信息熵[19]定义为

(11)

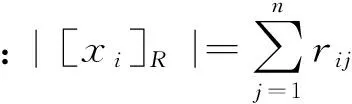
2.2 互补信息熵差异性度量方法

上节介绍的差异性度量方法不仅要求分类器的输出结果为0/1模式,而且需要预先判断分类器输出的正确性,无法直接度量分类器输出信息,不能适应连续或模糊数据的集成处理。互补信息熵则不仅能应用于模糊信息系统的信息处理,而且无需预先离散化,也可以度量分类器系统所蕴含的信息量。为此,本文将其用于分析分类器的差异性,提出一种采用互补信息熵的差异性度量方法。

假设分类器系统中基分类器ci的分类输出结果为Oi={oi1,oi2,…,oiN},将各基分类器的输出组合起来构成一个新的分类数据空间,即U={oij|i=1,…,L;j=1,…,N},其中,L表示分类器个数,N表示样本个数,每一个分类器的输出即为数据空间U中的一个数据对象,各个分类器间的差异性越大,则蕴含的互补信息熵也越大,由此得到一种新的差异性度量方法。

定义2 设O={o1,o2,…,oL}为有限非空论域,R是O上的任意模糊关系,则基于互补信息熵的差异性度量方法(Complement Information Entropy, CIE)定义为

(12)

式中:|[oi]R|表示在第i个分类器输出的各样本对象结果在模糊关系R下的势。

定义2基于不同分类器间的相似关系,综合度量基分类器对各个原始样本数据的分类效果及其互补信息,给出基分类器集合的差异性,省略了对分类器输出结果的正确性判别过程,具有更好的适应性。DCIE值越大,则差异性越大,可用于指导基分类器的评价和选择。为此,本文依据互补信息熵差异性度量方法提出增量式的基分类器差异重要性评价方法,其定义如下。

定义3 给定一个基分类器集成系统(O,C),O为有限非空论域,C为所有分类器集合,B⊆C,∀ci∈C-B,则分类器ci关于分类器集合B中的差异重要性定义为

S(ci,B)=DCIE(B∪{ci})-DCIE(B)

(13)

该定义以基分类器集成系统差异性增加为基本准则。若加入一个基分类器后,集成系统的差异性增加,则保留该分类器;若集成系统的差异性降低,则舍去该分类器。基于该准则可实现基分类器的自动选择,有利于降低集成规模。

2.3 基于互补信息熵差异重要性评价的选择性集成方法

为了验证CIE差异性度量方法与集成分类精度之间的关系,设计了一种基于互补信息熵分类器差异性评价的集成方法(简称CIE集成方法),即首先将原始数据集划分为训练集和测试集,然后采用Bootstrap采样方法在训练集上生成N个数据子集,再基于这些数据子集对基分类器进行训练得到每个数据对象的分类输出结果。在基分类器训练结束后,基于定义3评价当前分类器对基分类器集合的重要程度。如果重要性大于0,则保留该分类器;若重要性小于等于0,则舍去该分类器,继续评价下一个分类器。将选择的基分类器输出结果通过多数投票法进行组合,可得到最终的分类结果。

CIE集成方法步骤如下。

步骤1 初始条件。令U←有限数据集,C←初始空分类集成系统。

步骤2 生成训练子集。利用Bootstrap采样方法生成N个训练子集。

步骤3 训练基分类器。在每个训练子集上训练单一分类器,得到N个分类器集合{Ci}i=1,…,N。

步骤4 基分类器性能评价与选择。根据式(13)分类器差异重要性评价结果自动选择分类器加入集成系统C。

步骤5 生成分类器集成系统。将加入的各基分类器组合得到最终的分类器集成系统C*,利用多数投票方法组合输出结果。

步骤6 集成系统分类精度评价。基于10折交叉验证方法评价集成系统C*的分类精度。

CIE集成方法在运行过程中无需重复进行类别标记,利用差异性评价方法对在样本采样后的训练子集中生成的基分类器进行选择,不仅能够提高分类器间的差异性,也有助于降低分类器系统的集成规模和复杂度,提高系统的识别效果。

3 数据实验分析

3.1 实验数据

本文利用机器学习领域常用的加州大学Irvine分校UCI(University of California Irvine)数据库[20]中的12种数据集对CIE集成方法的性能进行验证实验,涉及医学诊断、客户分类、污水处理、车辆分析和葡萄酒识别等方面,详细信息如表1所示。12种数据集的类别数为2～13类,特征值均为数值类型,特征既有连续型,也有离散型,特征维数在4～56之间,样本数在32到1 000之间。

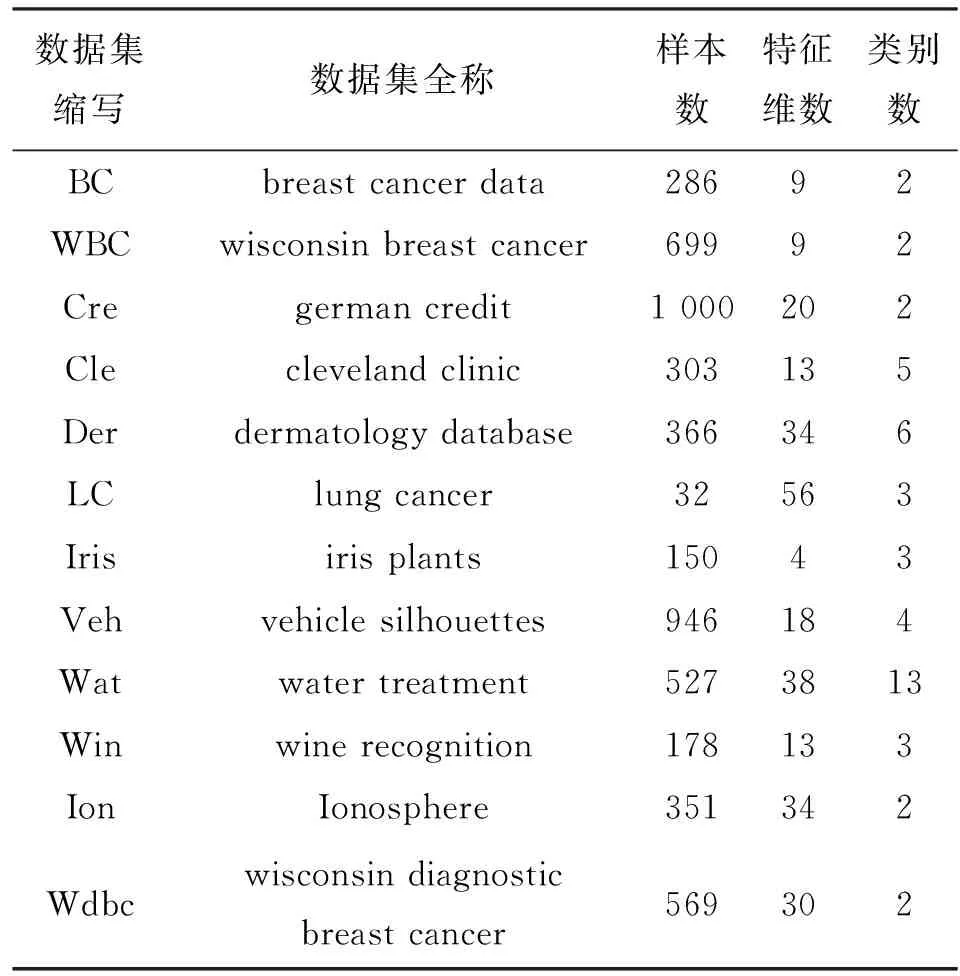
表1 UCI实验数据

3.2 CIE集成方法分类性能比较实验

在开始算法性能实验前,需首先设置基分类器的训练个数N,各方法的分类精度为P。从表1中随机选取Wbc、Cre、Wat和Wdbc 4个数据集,并选择常用的决策树(decision tree, DT)和支持向量机(support vector machine, SVM)作为基分类器,其中SVM核函数采用径向基函数。在此基础上,分析集成系统训练的基分类器数量对CIE方法集成分类性能的影响,实验结果如图1所示。

(a)WBC (b)Cre

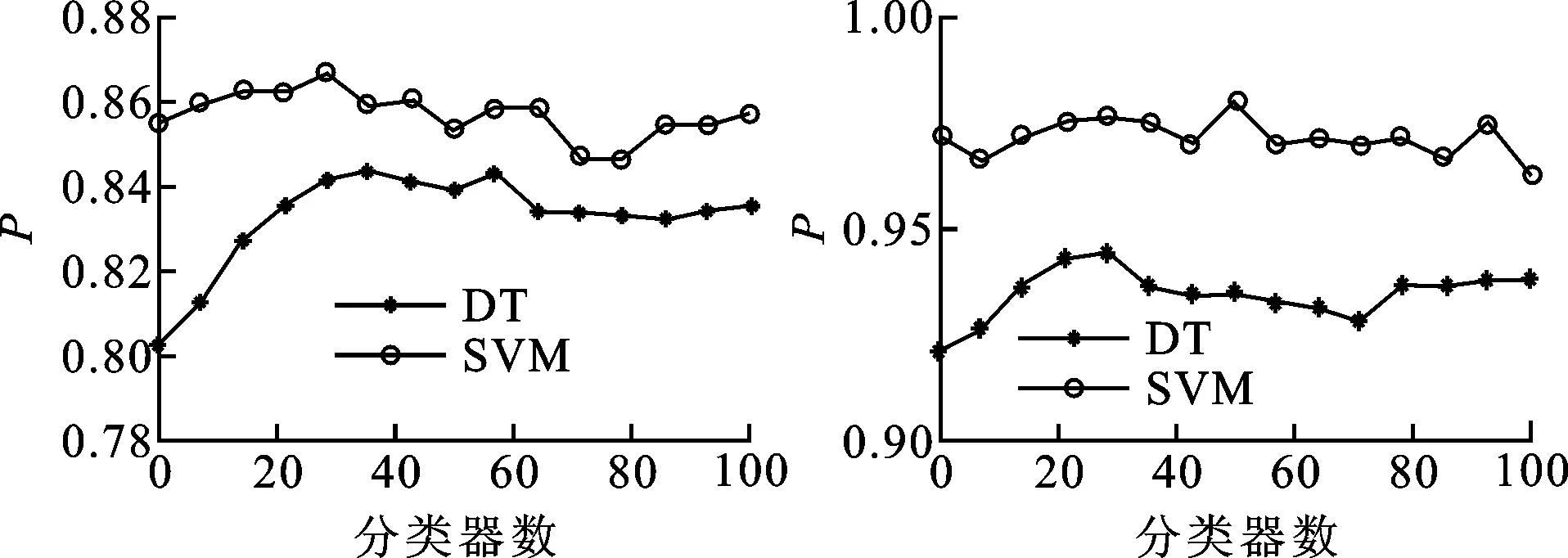
(c)Wat (d)Wdbc图1 不同基分类器数对算法分类性能的影响

由图1可知,随着分类器数量的增加,集成分类精度存在先升后稳的趋势,甚至还会降低,表明分类器数量并非越多越好,满足集成系统的选择需要即可。为提高集成系统的训练效率,以下统一设置N=10。

进行CIE集成方法的分类性能验证实验,并将结果与Bagging(Bag)、Adaboost(Ada)和RSM等主要集成算法进行分析比较。首先将数据集样本随机划分为20份,循环将其中9份组合作为训练集,剩余1份作为测试集,并在每个循环中生成10个基分类器作为候选集合,然后根据重要性评价方法自动选择合适的分类器组合得到分类器集成系统。Bagging、Adaboost和RSM等集成算法采用新西兰Waikato大学开发的WEKA机器学习软件对数据集进行分类实验。所有算法的参数设置均为WEKA的默认设置。

(a)BC (b)WBC

(c)Cre (d)Cle

(e)Der (f)LC

(g)Iris (h)Veh

(i)Wat (j)Win

(k)Ion (l)Wdbc图2 以决策树为基分类器时几种集成算法的分类性能比较

(a)BC (b)WBC

(c)Cre (d)Cle

(e)Der (f)LC

(g)Iris (h)Veh

(i)Wat (j)Win

图2和图3分别为采用决策树和SVM为基分类器时,上述方法在这些数据集上的分类性能比较结果。从图中结果可以得出:

(k)Ion (l)Wdbc图3 以SVM为基分类器时几种集成算法的分类性能比较

(1)CIE集成方法的分类性能在多数数据集上接近或超过Bagging、Adaboost和RSM算法,表明以差异性评价作为选择分类器的标准是可行的;

(2)当采用决策树为基分类器时,CIE集成方法在半数数据集上获得最优性能,而当采用SVM为基分类器时,CIE集成方法在8个数据集上性能表现突出,在Cle、LC、Iris、Wat和Wdbc这5个数据集上表现更为明显,如在Cle上的分类精度相比Bagging算法提高了38.5%。

3.3 CIE差异性度量方法性能分析实验

在CIE集成方法框架下,为了比较CIE度量方法与其他差异性度量方法的性能差异,引入Q统计、熵度量、KW方差和双错度量等常用方法替换CIE差异性度量方法,并与原始CIE集成方法进行比较。图4和图5是分别以决策树和SVM为基分类器时的精度对比结果。对图4、图5的结果分析可得如下结果。

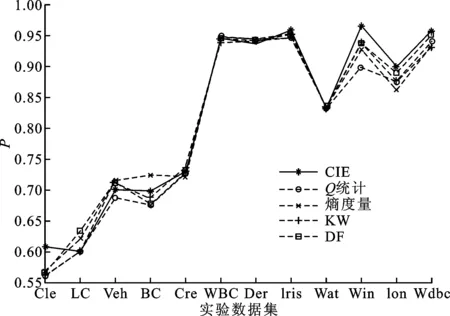
图4 以决策树为基分类器时几种差异性度量方法的集成分类性能比较

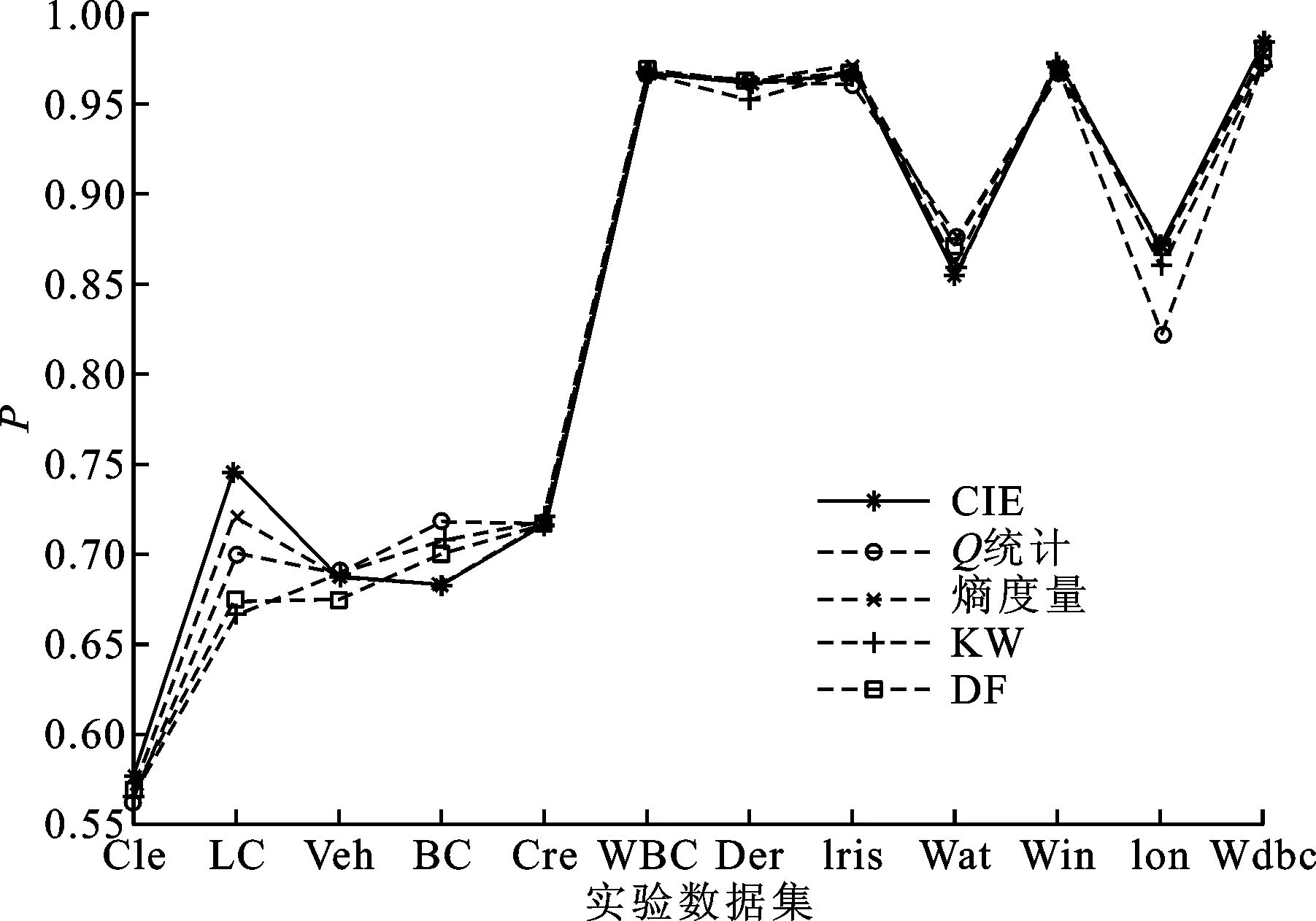
图5 以SVM为基分类器时几种差异性度量方法的集成分类性能比较

(1)采用决策树作为基分类器时,基于CIE度量集成后的系统分类精度与基于其他4种差异性度量方法相比,在6个数据集上获得最佳分类效果;采用SVM作为基分类器时也在4个数据集上获得最高精度;在其余数据集上的分类性能则与其他方法相近,表明CIE差异性度量方法可有效应用于分类器集成系统的差异性评价,并指导分类器集成系统设计和优化。

(2)通过对图4和图5实验结果的统计分析可以看出,CIE度量方法综合性能最优,在不同基分类器条件下均取得了最高平均分类精度,如表2所示。其次是熵度量和双错度量方法。熵度量和双错度量在文献[5]中也指出其具有较好的差异性度量能力,整体性能表现要优于Q统计和KW方差。

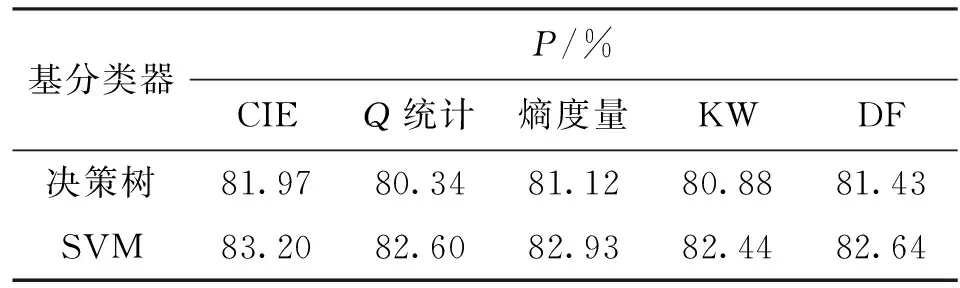
表2 几种差异性度量方法下CIE集成方法的

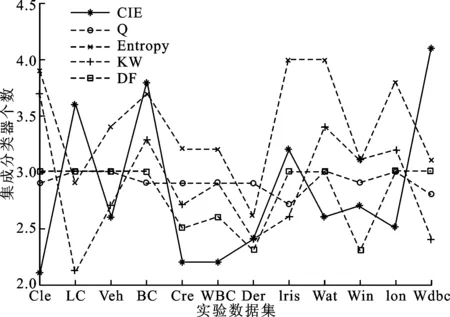
图6 以决策树为基分类器时几种差异性度量方法集成的分类器个数比较

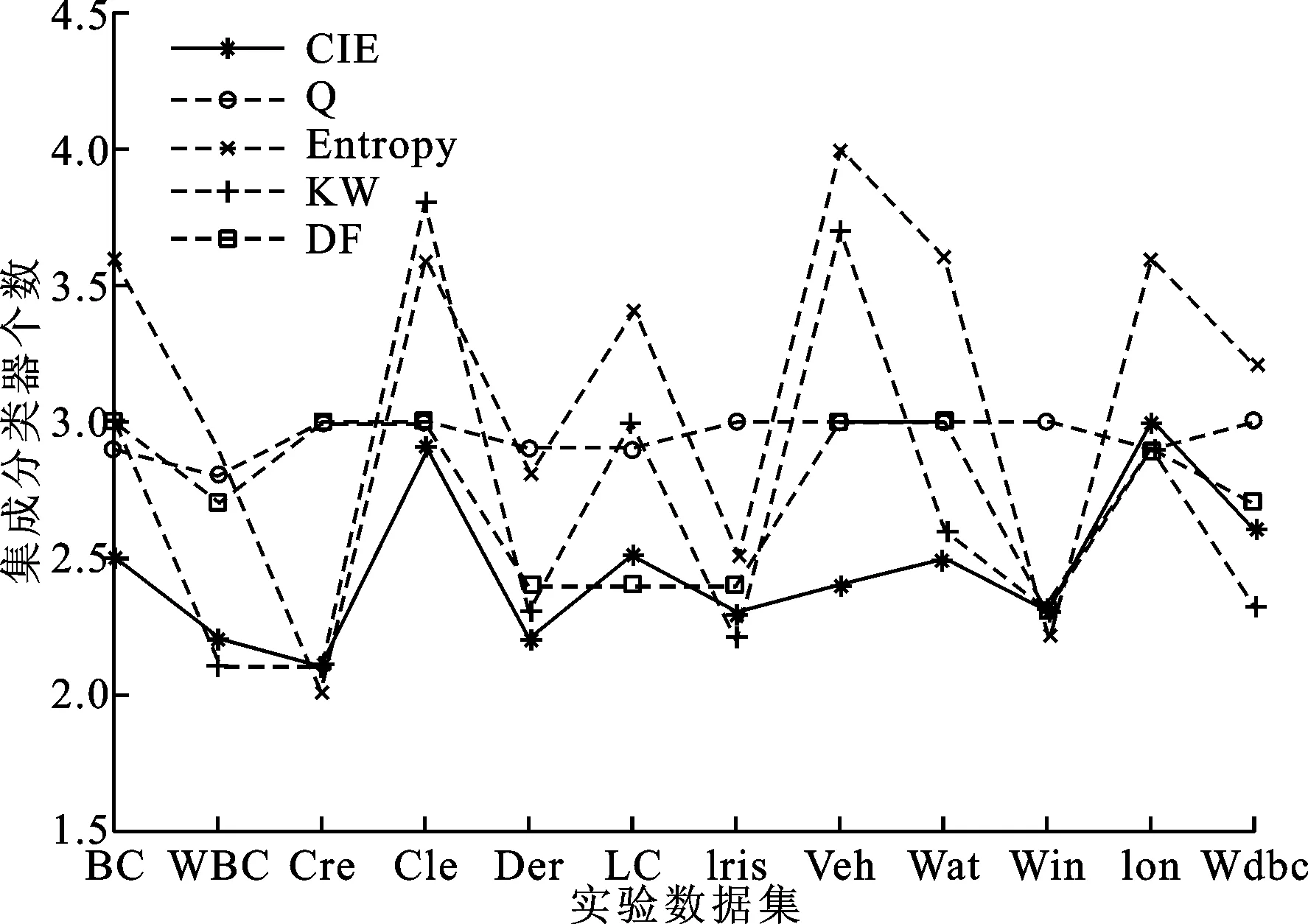
图7 以SVM为基分类器时几种差异性度量方法集成的分类器数比较

图6和图7给出了本节实验过程中,基于上述差异性度量方法的集成系统最终选择的基分类器个数。由图中可知,无论采用何种差异性度量方法,多分类器系统集成的平均分类器个数在2.1～4.0之间。与传统上多达几十甚至上百个分类器的复杂集成系统相比,CIE方法可在选择少量基分类器的同时,获得较优的分类性能,平均比Q统计方法生成的集成系统规模降低17%左右。

通过上述实验,基于CIE差异性评价的集成算法具有在选择较少基分类器的基础上,保持或提高分类器系统性能的能力。互补信息熵差异性度量方法在度量多分类器系统差异性方面是有效的,在分类器集成过程中的应用也是可行的。

4 结 论

为了满足直接度量分类器差异性的多样性需求,提高分类数据处理的能力,本文提出了一种互补信息熵差异性度量方法,并利用分类器重要性评价选择基分类器进行集成。该方法能够直接处理分类器的输出结果,不受0/1模式限制;此外,通过对分类器系统信息量的直接度量,省略了对分类结果正确性的判别,适用于半标记和未标记数据的处理。实验结果验证了本文方法在分类器集成应用方面的有效性和可行性。

需要指出的是,CIE集成方法在分类器选择过程中仅采用了差异性指标,虽然有效降低了系统的集成规模,但未考虑与集成精度的平衡问题,对系统的泛化能力可能会有一定影响。目前在如何实现分类器系统差异性和集成精度的有效平衡以及对系统的影响方面尚缺乏理论依据,下一步工作将在集成系统的优化方面进行研究和探索。

[1] KUNCHEVA L I, SKURICHINA M, DUIN R P W. An experimental study on diversity for bagging and boosting with linear classifiers [J]. Information Fusion, 2002, 3(4): 245-258.

[2] BROWN G, KUNCHEVA L I. “Good” and “bad” diversity in majority vote ensembles [C]∥Proceedings of International Conference on Multiple Classifier Systems. Berlin, Germany: Springer, 2010: 124-133.

[3] 张宏达, 王晓丹, 韩钧, 等. 分类器集成差异性研究 [J]. 系统工程与电子技术, 2009, 31(12): 307-3012. ZHANG Hongda, WANG Xiaodan, HAN Jun, et al. Survey of diversity researches on classifier ensembles [J]. Systems Engineering and Electronics, 2009, 31(12): 3007-3012.

[4] NASCIMENTO D, COELHO A, CANUTO A. Integrating complementary techniques for promoting diversity in classifier ensembles: a systematic study [J]. Neurocomputing, 2014, 138: 347-357.

[5] KUNCHEVA L I, WHITAKER C J. Measures of diversity in classifier ensembles and their relationship with the ensemble accuracy [J]. Machine Learning, 2003, 51: 181-207.

[6] WINDEATT T. Diversity measures for multiple classifier system analysis and design [J]. Information Fusion, 2005, 6(1): 21-36.

[7] HAGHIGHI M S, VAHEDIAN A, YAZDI H S. Creating and measuring diversity in multiple classifier systems using support vector data description [J]. Applied Soft Computing, 2011, 11(8): 4931-4942.

[8] KRAWCZYK B, WOZNIAK M. Diversity measures for one-class classifier ensembles [J]. Neurocomputing, 2004, 126: 36-44.

[9] YIN X C, HUANG K Z, HAO H W, et al. A novel classifier ensemble method with sparsity and diversity [J]. Neurocomputing, 2014, 134: 214-221.

[10]BI Y X. The impact of diversity on the accuracy of evidential classifier ensembles [J]. International Journal of Approximate Reasoning, 2012, 53(4): 584-607.

[11]AKSELA M, LAAKSONEN J. Using diversity of errors for selecting members of a committee classifier [J]. Pattern Recognition, 2006, 39(4): 608-623.

[12]RASHEED S, STASHUK D W, KAMEL M S. Diversity-based combination of non-parametric classifiers for EMG signal decomposition [J]. Pattern Anal Applic, 2008, 11(3/4): 385-408.

[13]杨春, 殷绪成, 郝红卫, 等. 基于差异性的分类器集成有效性分析及优化集成 [J]. 自动化学报, 2014, 40(4): 660-674. YANG Chun, YIN Xucheng, HAO Hongwei, et al. Classifier ensemble with diversity: effectiveness analysis and ensemble optimization [J]. Acta Automatica Sinica, 2014, 40(4): 660-674.

[14]杨长盛, 陶亮, 曹振田, 等. 基于成对差异性度量的选择性集成方法 [J]. 模式识别与人工智能, 2010, 23(4): 565-571. YANG Changsheng, TAO Liang, CAO Zhentian, et al. Pairwise diversity measures based selective ensemble method [J]. PR&AI, 2010, 23(4): 565-571.

[15]谷雨. 分类器集成中的多样性度量 [J]. 云南民族大学学报: 自然科学版, 2012, 21(1): 59-65. GU Yu. Measure diversity classifier ensemble [J]. Journal of Yunnan National University: Natural Science, 2012, 21(1): 59-65.

[16]LIU W Y, WU Z H, PAN G. An entropy-based diversity measure for classifier combining and its application to face classifier ensemble thinning [C]∥Proceedings of International Conference on Sinobiometrics. Berlin, Germany: Springer, 2004: 118-124.

[17]LIANG J, CHIN K, DANG C. A new method for measuring uncertainty and fuzziness in rough set theory [J]. International Journal of General Systems, 2002, 31(4): 331-342.

[18]YU D, HU Q, WU C. Uncertainty measures for fuzzy relations and their applications [J]. Applied Soft Computing, 2007, 7(3): 1135-1143.

[19]ZHAO J, ZHANG Z, HAN C, et al. Complement information entropy for uncertainty measure in fuzzy rough set and its application [J]. Soft Computing, 2015, 19(7): 1997-2010.

[20]BLAKE C L. MERZ C L. UCI repository of machine learning databases [EB/OL]. (2007-10-12) [2015-05-08]. http:∥www.ics.uci.edu/～mlearn/MLRepository.html.

[本刊相关文献链接]

兰景宏,刘胜利,吴双,等.用于木马流量检测的集成分类模型.2015,49(8):84-89.[doi:10.7652/xjtuxb201508014]

喻明让,张英杰,陈琨,等.考虑调整时间的作业车间调度与预防性维修集成方法.2015,49(6):16-21.[doi:10.7652/xjtuxb201506003]

杨宏晖,王芸,孙进才,等.融合样本选择与特征选择的AdaBoost支持向量机集成算法.2014,48(12):63-68.[doi:10.7652/xjtuxb201412010]

王羡慧,覃征,张选平,等.采用仿射传播的聚类集成算法.2011,45(8):1-6.[doi:10.7652/xjtuxb201108001]

马超,陈西宏,徐宇亮,等.广义邻域粗集下的集成特征选择及其选择性集成算法.2011,45(6):34-39.[doi:10.7652/xjtuxb201106006]

(编辑 刘杨)

A Novel Measure Method for Diversity of Classifier Integrations Using Complement Information Entropy

ZHAO Junyang1,2,HAN Chongzhao2,HAN Deqiang2,ZHANG Chunxia3

(1. Staff Room 202, The Second Artillery Engineering University, Xi’an 710025, China; 2. School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 3. School of Mathematics and Statistics,Xi’an Jiaotong University, Xi’an 710049, China)

A novel diversity measure method using complement information entropy (CIE) is proposed to solve the problem that the diversity estimation of multiple classifier systems is unable to deal directly with fuzzy data. A set of base classifiers is generated by using training data, and then is used to label test data. The outputs of the classifiers are reorganized into a new classification data space. Then the complement information entropy model is introduced under fuzzy relation to measure uncertainty information of the new space and the uncertainty information is used to estimate the diversity of base classifiers. Finally, an ensemble system is constructed based on the criterion that the ensemble diversity of the classifier set increases when a base classifier is added, and the ensemble system is used to validate the performance of CIE. Experimental results and a comparison with theQ-statistic method show that the average classification accuracy of CIE increases by 2.03%, and the number of ensemble classifiers reduces by 17%. Moreover, CIE also improves the ability of ensemble systems to process diverse data.

classifier ensemble; diversity; complement information entropy; fuzzy relation

2015-06-21。

赵军阳(1981—),男,讲师,博士后;韩崇昭(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61074176,41174162);中国博士后科学基金资助项目(2013M532048)。

时间:2015-11-27

10.7652/xjtuxb201602003

TP391.4

A

0253-987X(2016)02-0013-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151127.2115.002.html