一种仿生鱼体自主游动的水动力学特性分析

严惠云,张浩磊,刘小民

(1.西北工业大学理学院, 710072, 西安;2.西安交通大学能源与动力工程学院, 710049, 西安)



一种仿生鱼体自主游动的水动力学特性分析

严惠云1,张浩磊2,刘小民2

(1.西北工业大学理学院, 710072, 西安;2.西安交通大学能源与动力工程学院, 710049, 西安)

针对金枪鱼结构和自主游动现象建立了仿生鱼体几何模型及鱼体摆动计算模型,采用计算流体动力学Fluent软件结合动网格技术,编写了控制鱼体摆动的UDF程序,对仿生鱼慢速自主巡游状态和C形快速起动状态进行了数值模拟,研究了鱼体摆动频率和摆动方式对仿生鱼周围压力、速度、涡量分布以及鱼体受力状态的影响,揭示了仿生鱼自主游动过程的水动力学特性。研究结果表明:在自主巡游阶段,仿生鱼通过摆动鱼体,在鱼体两侧流场产生高压和低压区,依靠流体的正压梯度获得前进的推动力;在C形快速起动阶段,仿生鱼通过快速大幅度的回摆获得加速度,从而实现快速起动。鱼体自主游动水动力学特性的研究将为仿生水下推进器的概念设计和性能优化提供重要的参考。

仿生机器鱼;自主游动;水动力学;数值模拟

水下推进器是探索和开发海洋的重要工具。相比于传统水下推进器,仿鱼形水下推进器由于在运动形态控制方面具有较大的优势,近些年来受到了研究者的热切关注。

Deng等数值模拟了二维的鱼类游动,研究了不同控制参数下鱼体的推力性能及其周围的流场结构[1]。Liu等基于CFD方法实现了对复杂生物体运动的可视化建模,数值分析了蝌蚪游动的三维流场[2]。Liu等对柔性的月牙形尾鳍和矩形尾鳍在非定常大摆幅游动时的推进机理进行了数值模拟,结果表明在负荷较大的情况下,月牙形尾鳍的推进效率要高出10%以上[3]。Carling等通过求解二维N-S方程,对鱼类鳗鲡模式游动进行仿真,分析其游动过程中的受力情况[4]。Zhu等利用三维面元的方法分析了金枪鱼游动时的水动力学特性,研究了尾鳍对旋涡的主动控制以及受旋涡的影响[5]。Hu等分析了鳗鲡倒退游动的动力学特性,指出这种游动方式是结构最优的[6]。夏全新等利用动网格模型,采用有限体积法对鱼类波状摆动推进模式进行了数值仿真[7]。童秉纲等相继对鱼类机动和巡游运动进行了数值模拟,发现鱼体推动力主要来自尾鳍边缘的旋涡[8-10]。Kern等优化分析了鳗鲡的波动运动方式,并给出了三维的尾迹涡环结构[11]。Borazjani等分别对黏性流和惯性流中的鳗鲡模式和鲹科模式进行了水动力学研究,分析了St和Re对游动性能的影响[12]。王亮等通过数值模拟二维仿生鱼群的机动和巡游过程,提出了一种鱼类自主游动的控制方法[13-14]。

为了揭示仿生鱼自主游动过程中不同巡游状态的水动力学特性,从而为水下推进器的概念设计和性能优化提供参考,本文在总结前人研究成果的基础上,采用Fluent软件对所建立的二维仿生鱼自主游动过程进行数值模拟,详细分析了不同游动过程中鱼体周围的压力、速度、涡量分布,并针对仿生鱼的受力状态进行了分析,揭示了鱼体自主游动过程中推进力的产生机理。

1 仿生鱼体模型与数值方法

根据金枪鱼实体结构,忽略鱼体腹鳍和尾鳍,考虑到鱼体的对称性,建立仿金枪鱼二维几何模型,如图1所示。鱼体从头部到尾端的长度设为L。

图1 金枪鱼及仿生金枪鱼二维几何模型

仿生鱼体的绕流控制方程为

(1)

式中:u是流体速度;p是流体压力;ρ是流体密度;ν是流体的动力学黏性系数。

针对二维仿生鱼自主游动状态,给出其受力控制方程为

(2)

式中:M是仿生鱼的质量;U是仿生鱼的游动速度;F是仿生鱼在速度方向上受到的合力。

计算区域设置为5L×1.5L,其中鱼体头部距离上游进口边界为1.65L,尾鳍距离下游出口边界为2.35L,如图2所示。为了保证仿生鱼体边界运动过程中动网格的质量,本文采用近似光顺模型和局部重构模型组合进行网格质量的控制,对局部粗网格重新细化,对变形较大的网格进行光顺处理。计算区域非结构化网格由Gambit生成,采用Fluent软件中的动网格模型,编写了相应的UDF程序,对鱼体的运动边界进行控制,从而实现鱼体摆动过程中相应网格的动态变化。

图2 计算区域网格划分及仿生鱼体尾部网格布置

为了简化计算,假定仿生鱼在计算区域中某位置处固定,鱼体以给定的参数方式进行摆动,水相对于鱼体以一定的速度向下游流动。针对鱼体所建立的坐标系下,给出鱼体中线的摆动规律[12]为

h(x,t)=a(x)sin(ωt-2πkx)

(3)

式中:h(x,t)表示鱼体中心线的侧向位移;x表示鱼体中心线沿体长方向上的位置坐标,且-0.35≤x≤0.65;a(x)为波幅包络线函数;k为鱼体波的数量,本研究中取k=1,得到鱼体波长λ=L/k=L,其中L为鱼体特征长度;ω为鱼体摆动的角频率,ω=2πf,其中f为仿生鱼体的摆动频率。

计算中进口处给定速度边界条件,进口速度为仿生鱼巡游过程的平均速度值;出口处给定压力边界条件,压力值为0 Pa(参考压力为大气压)。湍流计算采用标准k-ε两方程湍流模型。时间步长为0.005 s,总计算时间为5 s,残差收敛条件设定为0.000 1。网格数分别选取为1.4×105、1.8×105、2.1×105、2.25×105和2.5×105进行数值模拟计算。参考徐晓锋在仿生鱼游动数值模拟过程中关于网格无关性的验证方法[15],监测定常条件下X=L处Y方向上压力的变化情况,进行本文数值计算的网格无关性验证,计算结果如图3所示。从图中可以看出,当网格数超过2.25×105,X=L处Y方向上静压分布几乎不再发生变化,表明继续加密网格对计算结果影响不大。综合考虑计算精度和效率,本文在数值模拟计算中采用的网格数为2.25×105。

——一段时间内，四川省广安市委原副书记严春风、重庆市渝北区委原常委吴德华、海南省社会主义学院原院长施耀忠等一批表面洁身自好，作风正派，实则道貌岸然，腐化堕落的“两面人”相继被查处。对此，北京大学廉政研究中心副主任庄德水认为，必须改变一些地方干部考核走形式的现状，扩大干部考核评价的主体和范围，多渠道多方式多侧面了解一个干部的品行和业绩。组织部门应当给正直的干部撑腰，多关注勤勤恳恳干事的干部，防止被投机者、取巧者所误导。（《中国纪检监察报》11月15日）

图3 X=L处Y方向上压力分布

以仿生鱼体长L为特征常数,沿鱼体体干方向为X方向,垂直体干方向为Y方向,对模型参数及相关物理量进行无量纲化处理。仿生鱼体X方向、Y方向的作用力系数以及Z方向作用力矩系数描述为

(4)

式中:u表示仿生鱼游动速度;ρ为流体密度;CD表示X方向作用力系数;CL表示Y方向作用力系数;CM表示力矩系数;Fx、Fy、Mz分别表示X、Y方向的作用力及Z方向的作用力矩。

最大侧向力系数,即Y方向的作用力系数的最大值表述为

(5)

式中:CLmax表示最大侧向力系数;Fymax表示Y方向的最大瞬时作用力。

2 数值结果及分析

2.1 仿生鱼巡游过程的数值模拟

图4为第8个摆动周期到第9个摆动周期内,仿生鱼周围流场压力分布情况,图中T为仿生鱼体摆动周期。可以看出:仿生鱼躯干的后半部分,从t=(8+0/10)T开始由前到后逐渐向上弯曲,到t=(8+5/10)T时,仿生鱼两侧的流场形成两个压力中心,压力梯度从上方指向下方。在这个过程中,尾鳍的摆动幅度从零(平衡位置)到负的最大(最低极限位置)然后又变成零(平衡位置)。具体过程为:t=(8+0/10)T到t=(8+2/10)T时,鱼尾从平衡位置向下方运动,与X方向成负角,尾部下方的流场形成高压区域;t=(8+3/10)T到t=(8+5/10)T时,鱼尾回到平衡位置并继续向上方运动,与X方向成正角,在尾部上方的流场形成高压区域。仿生鱼体继续发生形变,两个压力中心同时慢慢的向仿生鱼的后方转移,最后在鱼尾处脱落并形成旋涡。同样,t=(8+5/10)T到t=(9+0/10)T时,鱼体后半部分从前至后逐渐向下波动,而前半周期鱼体前方产生的高压中心逐渐移动到鱼体后方,最终在鱼尾处脱落并形成旋涡。

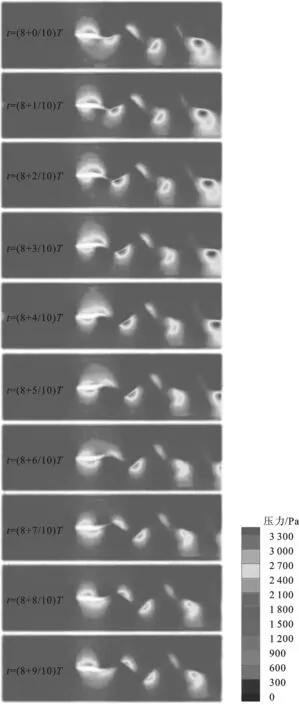
图4 一个周期内仿生鱼周围流场压力分布

图5为仿生鱼游动过程中鱼体受力状态随时间的变化情况。X方向作用力提供仿生鱼向前游动的推力,Y方向作用力使仿生鱼在向前游动的同时发生垂直于速度方向的平动,作用力矩使鱼体绕质心做小幅度的摆动。由图可见,X和Y方向的作用力系数CD与CL以及力矩系数CM都呈现出典型的周期性变化。在t=(8+3/10)T和t=(8+8/10)T两个时刻,CD和CM达到最大值,结合压力云图发现这两个时刻高压区域与鱼体接触面积最大,这也就是鱼类在巡游过程中具有较大推进力的原因。

图5 仿生鱼巡游过程中受力随时间的变化

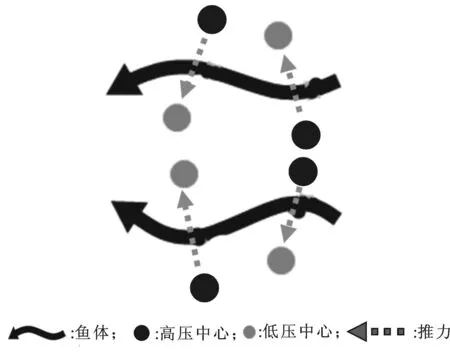
图6 仿生鱼受力分析示意图

为了直观地表示仿生鱼体自主游动的推进原理,这里首先给出鱼体的受力示意图,如图6所示。由图6可以看出,无论鱼体摆动到什么位置,其两侧都会形成一个高压中心和一个低压中心,而且鱼体中部和尾部的压力中心分布刚好相反。也就是说,在鱼体摆动周期的任何时刻,在鱼体两侧始终存在着正压梯度,前半周期给鱼体向前和向下的压力分量,后半周期给鱼体向前和向上的压力分量,向前的压力分量为自主游动过程中的仿生鱼提供持续的推进力,而方向呈周期性变化的侧向力使鱼体在自主游动时向两侧平动。

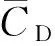
图与f的关系

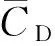
2.2 仿生鱼C形快速起动的数值模拟

仿生鱼的C形快速起动主要用于快速起动和转向的情况。根据对仿生鱼C形起动过程图像的研究,仿生鱼体前半段基本保持相对静止,主要依靠鱼体后半段的大幅度摆动来获得快速起动力,得到C形起动过程中仿生鱼体中线运动规律[16]为

(6)

(7)

式中:R(t)表示鱼体中线后半段摆动过程中曲率半径随时间的变化函数;x表示鱼体中线沿体干纵向坐标;a表示鱼体中线上某点到头部顶端的弧长;lh表示鱼体中线前段的总弧长;h表示鱼体中线沿摆动方向的横坐标;t为C形起动的持续时间。

鱼类的快速起动是一个在极短时间内复杂的鱼体与水流相互作用的非定常过程,这里仅考虑仿生鱼在静水中固定位置处的摆动,研究仿生鱼快速摆动过程中鱼体的受力情况及其随时间的变化。为此,在计算中进口边界处速度设定为0,模拟C形起动过程的总计算时间设定为0.50 s,时间步长为0.000 5 s。其中0～0.30 s是前摆过程,0.30～0.50 s是后摆过程。将C形起动过程分为8个离散的时刻,对每个时刻鱼体周围的压力、速度、流线进行分析。

前摆过程的4个时刻分别为0、0.10、0.20、0.30 s。后摆过程的4个时刻分别为0.35、0.40、0.45、0.50 s。图8为C形快速起动过程中流场压力分布,由图8a～图8h可见,前摆过程虽然所用时间长,但流场的变化相对于后摆过程并不明显。前摆过程中,鱼体周围流场的压力变化较小,鱼体上方出现低压区,下方出现高压区,但压差较小;后摆过程中,流场压力变化明显,尤其是刚开始反向摆动的时候,鱼体上方流场形成低压中心,下方形成高压中心,仿生鱼体大幅度反方向摆动时受到流场的作用力较大,表现出较大的推进力。

图9所示为在鱼体C形起动过程的一个摆动周期T内的8个不同时刻的流线分布。由图9a～图9h可见,仿生鱼尾鳍前摆过程中,在鱼体后方产生一个顺时针的旋涡,后摆过程中又产生一个逆时针的旋涡。随着鱼体的摆动,两个旋涡先后脱落并最终在鱼体后方形成一个涡环,如图10所示。

图11为C形起动过程中,仿生鱼沿体干方向的作用力CD随时间的变化。从图中可以看出:起动刚开始,鱼体从静止开始摆动,CD为正,鱼体所受阻力大于推力;然后由于前摆而产生第一个涡,鱼体受到压力梯度作用,推力大于阻力,CD变为负值且绝对值越来越大;尾鳍摆幅达到最大并开始回摆时,鱼体所受正压梯度突然增大,鱼体与高压中心接触面积最大,CD绝对值突然增大,推力达到最大值,仿生鱼实现快速起动;随后尾鳍继续回摆,合力逐渐减小直至为零,仿生鱼C形起动完成。

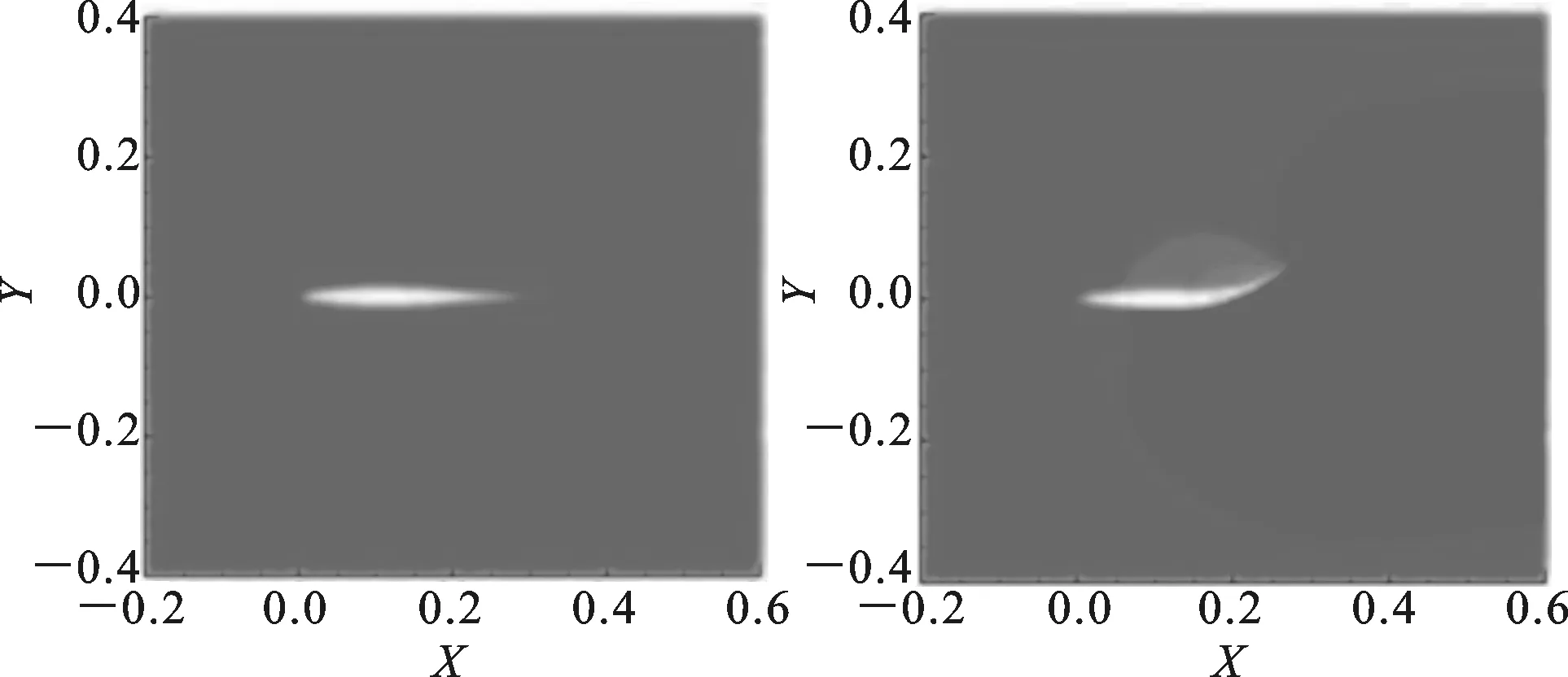
(a)t=0.00 s (b)t=0.10 s

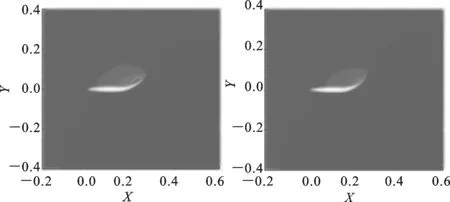
(c)t=0.20 s (d)t=0.30 s

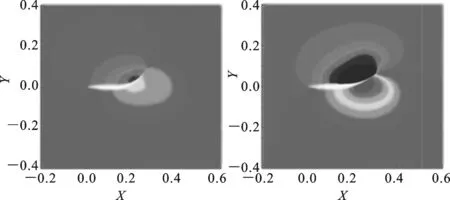
(e)t=0.35 s (f)t=0.40 s

(g)t=0.45 s(h)t=0.50 s

图8 仿生鱼体C形起动过程压力分布

(a)t=(0/8)T (b)t=(1/8)T

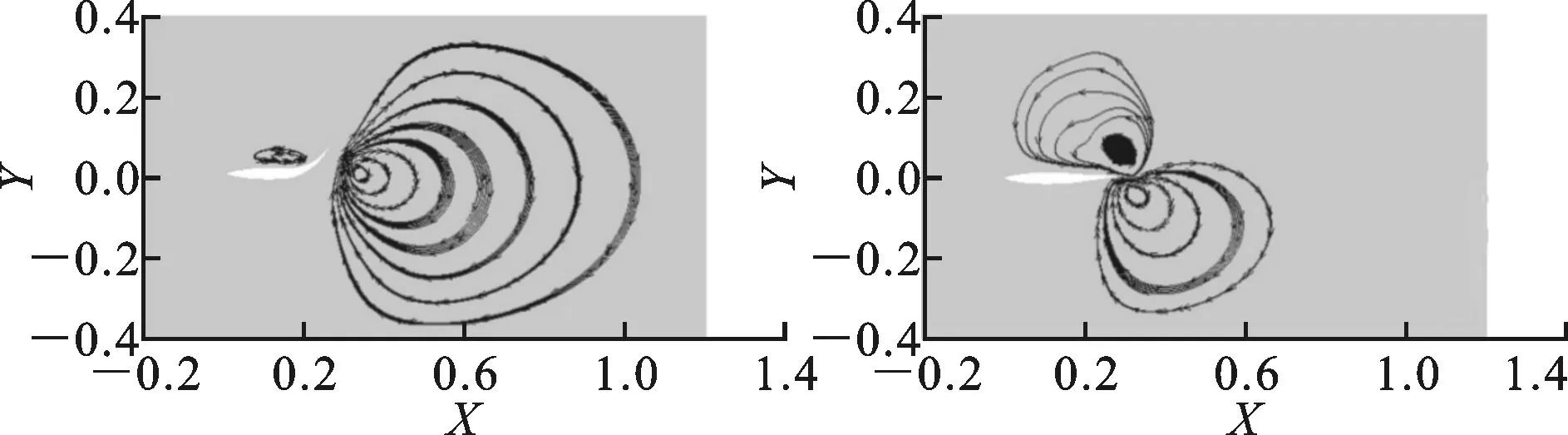
(c)t=(2/8)T (d)t=(3/8)T

(e)t=(4/8)T (f)t=(5/8)T

(g)t=(6/8)T (h)t=(7/8)T图9 仿生鱼体C形起动过程中鱼体周围流线分布

图10 仿生鱼体C形起动过程形成的涡环

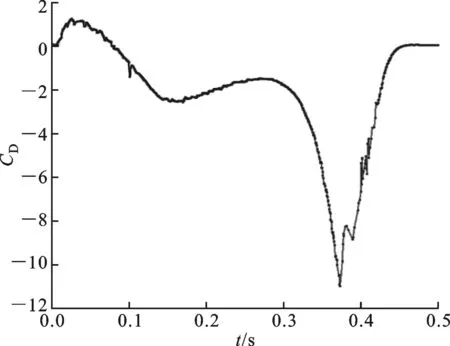
图11 C形起动过程仿生鱼沿体干方向作用力系数CD随时间的变化

3 结 论

(1)仿生鱼巡游过程中,鱼体通过摆动,引起周围流场的变化,在其鱼体两侧形成高压中心和低压中心,正压梯度向前的分量推动仿生鱼向前游动。随着摆动频率的增大,仿生鱼体受到的侧向推力越来越大。

(2)仿生鱼在C形快速起动过程中,前摆阶段是准备过程,耗时长但引起的流场变化小,在鱼体后方形成一个较小强度的旋涡;后摆阶段是主要过程,短时间内通过大幅度大角速度的回摆引起流场剧烈变化,鱼体两侧压力梯度为仿生鱼提供了加速度,并在鱼体后方形成一个较大强度的旋涡。两个旋涡方向相反,脱落后在鱼体后方形成一个涡环。

鱼类在水中游动是一个复杂的运动状态,本研究主要是通过模拟金枪鱼的二维自主巡游和C形快速起动过程,数值分析仿生金枪鱼的受力及其引起的鱼体周围流场的变化。在进一步的研究中,鱼体与水流相互作用、鱼体不同摆动规律以及三维仿生鱼体结构对鱼体运动状态的影响等都是重要的研究内容。

[1] DENG J, SHAO X M, REN A L. Numerical study on propulsive performance of fish-like swimming foils [J]. Journal of Hydrodynamics: Series B, 2006, 18(6): 681-687.

[2] LIU H, WASSERSUG R J, KAWACHI K. A computational fluid dynamics study of tadpole swimming [J]. Journal of Experimental Biology, 1996, 199(6): 1245-1260.

[3] LIU P, BOSE N. Propulsive performance from oscillating propulsors with span-wise flexibility [J]. Proceedings of the Royal Society of London: Series A, 1997, 453: 1763-1770.

[4] CARLING J, WILLIAMS T L, BOWTELL G. Self-propelled anguilliform swimming: aimilaneous aolution of the two-dimensional Navier-Stokes equations and Newton’s laws of motion [J]. Journal of Experimental Biology, 1998, 201(14): 3143-3166.

[5] ZHU Q, WOLFGANG M J, YUE D K P. Three-dimensional flow structures and vorticity control in fish-like swimming [J]. Journal of Fluid Mechanics, 2002, 468: 1-28.

[6] HU W R, TONG B G, LIU H. A computational study on backward swimming hydro dynamics in the eel anguilla [J]. Journal of Hydrodynamics, 2005, 17(4): 438-447.

[7] 夏全新, 鲁传敬, 吴磊. 鱼类波状摆动推进的数值模拟 [J]. 水动力学研究与进展: A辑, 2005, 20(S1): 921-928. XIA Quanxin, LU Chuanjing, WU Lei. Numerical simulation about fish undulating advancing [J]. Journal of Hydrodynamics: Series A, 2005, 20(Sl): 921-928.

[8] 童秉纲. 鱼类波状游动的推进机制 [J]. 力学与实践, 2000, 22(3): 69-74. TONG Binggang. Undulatory propulsion mechanism of fish swimming [J]. Mechanics and Engineering, 2000, 22(3): 69-74.

[9] LU X Y, YANG J M, YIN X Z. Propulsive performance and vortex shedding of a foil in flapping flight [J]. Acta Mechanica, 2003, 165(3): 189-206.

[10]LU X Y, YIN X Z. Propulsive performance of a fish-like traveling wavy wall [J]. Acta Mechanica, 2005, 175(1/2/3/4): 197-215.

[11]STEFAN K, PETROS K. Simulation of optimized anguilliform swimming [J]. Journal of Experimental Biology, 2006, 209(24): 4841-4857.

[12]IMAN B, FOTIS S. Numerical investigation of the hydrodynamics of carangiform swimming in the transitional and inertial flow regimes [J]. Journal of Experimental Biology, 2008, 211(10): 1541-1558.

[13]王亮, 王明, 付强. 串列仿生鱼自主游动的数值模拟研究 [J]. 计算力学学报, 2013, 30(5): 727-732. WANG Liang, WANG Ming, FU Qiang. Numerical simulation of two self-propelled fish swimming in a tandem arrangement [J]. Chinese Journal of Computational Mechanics, 2013, 30(5): 727-732.

[14]王亮, 王明, 付强, 等. 并列仿生鱼自主游动的数值模拟研究 [J]. 计算力学学报, 2014, 31(1): 103-109. WANG Liang, WANG Ming, FU Qiang, et al. Numerical simulation of two self-propelled fish swimming in a side-by-side arrangement [J]. Chinese Journal of Computational Mechanics, 2014, 31(1): 103-109.

[15]徐晓锋. 仿生鱼游动与运动控制的数值分析技术 [D]. 上海: 上海交通大学, 2011.

[16]陈宏. 仿生机器鱼巡游和机动的机理研究 [D]. 长沙: 中国科技大学, 2006.

(编辑 武红江 苗凌)

Numerical Analysis of Hydrodynamics Characteristics for Autonomous Swimming of Bionic Tunas

YAN Huiyun1,ZHANG Haolei2,LIU Xiaomin2

(1. School of Science, Northwestern Polytechnical University, Xi’an 710072, China;2. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

A two-dimensional computational model for the bionic tuna is established according the structure and swimming characteristics of tuna fishes and a UDF program for controlling the swing of the fish body is coded. The low speed cruise state and C shape rapid start behavior of the bionic fish in the process of autonomous swimming are numerically simulated by using the computational fluid dynamics software Fluent with the dynamic mesh technique. The effects of the swing frequency and swing mode of bionic fishes on the distributions of pressure, velocity and vorticity around their bodies are investigated, and the stress state of their bodies is also analyzed. The corresponding hydrodynamics characteristics of their autonomous swimming are revealed. The results show that, the bionic fish swings its body to produce an high pressure area and a low pressure area on its both sides and to obtain the propulsive force from the positive pressure gradient in the flow field in cruise stage and that it produces the propulsive force and accomplishes a rapid start through fast and large backswings in the C shape rapid start stage. The study presented in this paper will provide an important reference for the conceptual design and performance optimization of bionic underwater propulsions.

bionic robot fish; autonomous swimming; hydrodynamics; numerical simulation

2015-07-10。

严惠云(1977—),女,讲师。 基金项目:陕西省科学技术研究发展计划资助项目(2014K06-24)。

时间:2015-12-09

10.7652/xjtuxb201602023

O35;TP24

A

0253-987X(2016)02-0138-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151209.1635.002.html