压电俘能器涡激振动俘能的建模与实验研究
宋汝君,单小彪,李晋哲,谢涛
(1.哈尔滨工业大学机电工程学院, 150001, 哈尔滨;2.东北林业大学机电工程学院, 150040, 哈尔滨)
压电俘能器涡激振动俘能的建模与实验研究
宋汝君1,单小彪1,李晋哲2,谢涛1
(1.哈尔滨工业大学机电工程学院, 150001, 哈尔滨;2.东北林业大学机电工程学院, 150040, 哈尔滨)
针对微机电系统和传感器等低能耗电子产品的持续供能问题,提出了一种涡激振动式压电俘能器。该俘能器由压电悬臂梁和末端圆柱体组成,结构简单,可在较低水流流速下产生涡激共振,得到较大的能量输出。通过数学建模和实验测试的方法,研究了水流速度和外接电阻对压电俘能器振动和俘能的影响规律。实验结果表明:压电俘能器的振动频率随流速的增大而增大,振动幅值在涡激共振时最大,输出功率受流速和外接电阻两者影响,较小外接电阻适合较高流速,较大电阻适合较低流速,压电俘能器在涡激共振处可获得最大的能量输出,当外接电阻为0.5 MΩ、流速为0.41 m/s时,实验测试得到了8.3 μW的最大输出功率。数值分析结果与实验测试结果吻合较好,验证了数学模型的正确性。
水流;涡激振动;压电俘能器;俘能
随着集成电路、MEMS和微传感器等低能耗电子产品的发展,电池供能的方式存在质量大、体积大、存储有限、需要定期更换等诸多弊端,因此亟需一种可持续的能源供给方式。同时,环境振动能分布广泛,有水动能、风动能、潮汐能、机械振动能等,其中水动能是一种清洁的可再生能源。压电俘能器是一种结构简单、环境友好、使用寿命长久和无电磁干扰的振动能转换装置,可转换水动能为电能,能够满足低能耗电子产品的供能需求[1]。
既往的研究中,压电俘能器的研究重点集中在俘能器本身结构和俘能性能上,忽略了压电俘能器与环境振动的相互耦合影响[2-3]。水流激励压电俘能同时考虑了环境振动与俘能器本身的耦合影响,同时涉及流体场、固体场和电场,是一个多物理场相互耦合的能量转换技术,具有较高的学术研究价值,目前已经得到了国内外研究者的重视。本课题组也从俘能器本身构型的研究[4-6]逐渐转向压电俘能器耦合流体环境的研究上[7-8]。压电俘能器的流致振动俘能技术按照流激振动形式可分为尾流驰振式[9-10]、涡激振动式[11-12]、拍振式[13-14]和驰振式[15-17]等4种。尾流驰振式压电俘能器可工作于较低流速下,具有较宽的振动频带,但激励响应较小。涡激振动式压电俘能器多以尾端圆柱与压电振子构成,可在较低流速下(如低速水流)产生涡激共振使压电俘能器的振动幅值和能量输出最大;且由于“锁定”现象的存在,涡激共振区域增大,工作频带增宽。驰振式和拍振式压电俘能器在流体激励下具有相同的振动特征,即振幅发散式增幅振动,它存在一个临界速度,当来流流速低于临界速度时,压电俘能器静止,当速度大于临界速度时,其振动幅值随速度的增大而逐渐增大,因此拍振式和驰振式压电俘能器更适合于较高流速环境下(如风流)。
综上发现,涡激振动式压电俘能器适合于水流激励下振动俘能,然而现有的研究主要围绕空气流进行[11-12]。相比于空气,水流一般流速较小,但具有较大的密度和黏度。因此,流体激励力、激励频率、流体附加质量和附加黏度对压电俘能器的振动俘能的影响截然不同。鉴于此,本文提出了一种由压电悬臂梁和末端圆柱体组成的涡激振动式压电俘能器,并建立了压电俘能器振动响应和能量输出的数学模型,分别分析了水流流速和外接电阻等参数对俘能器振动和发电能力的影响规律,并设计压电俘能器样机,通过实验研究了压电俘能器在水流环境下的功率输出。
1 结构及数学模型
圆柱绕流是自然界较为常见的现象,当流体流过任何非流线型物体时,都会在物体两侧交替产生脱落的旋涡,交替脱落的旋涡会在垂直于来流方向产生周期性变化作用力。周期性作用力可激励弹性固支的压电俘能器振动并发电,图1给出了涡激振动压电俘能系统示意图和尺寸图。

(a)涡激振动压电俘能系统三维示意图
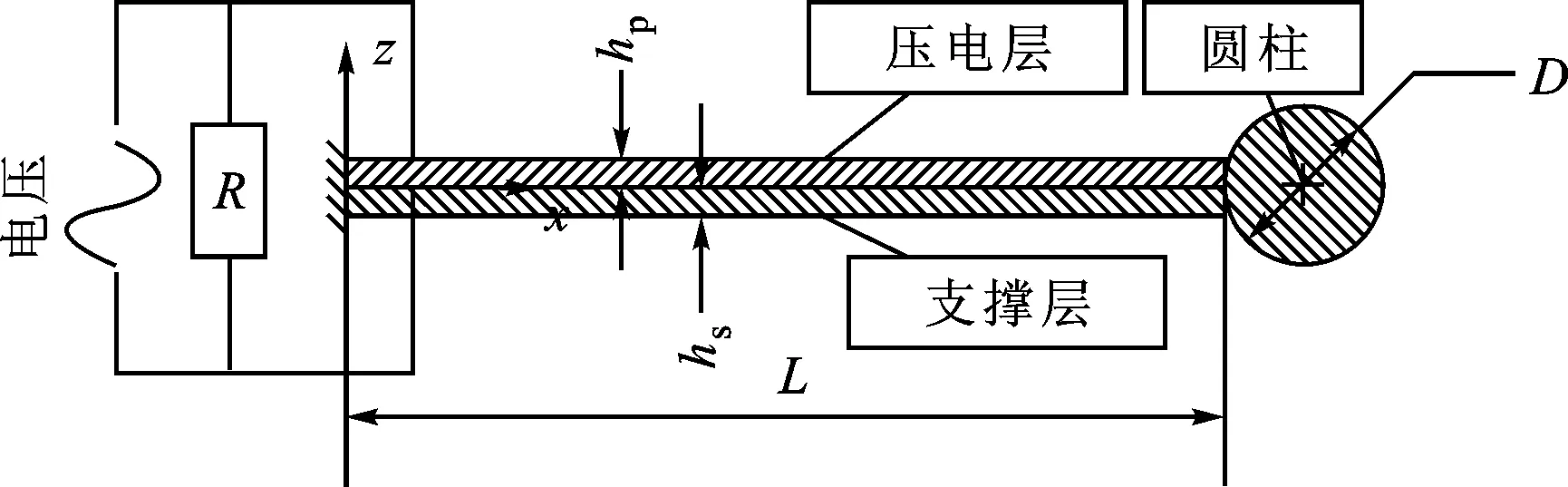
(b)压电俘能器尺寸图图1 涡激振动压电俘能系统示意图和尺寸图
由图1可知,压电俘能器由压电悬臂梁自由端与圆柱连接组成。压电梁长度为L,宽度为b,分别由厚度为hs的支撑层和厚度为hp的压电层组成。圆柱体直径为D,长度为Lc,外接电阻为R。
假设压电悬臂梁为线性变形并仅发生在z方向上,压电悬臂梁运动的离散控制方程表示为
dδ(x-L)/dx]=Ftδ(x-L)
(1)

根据Facchinetti等的研究,圆柱涡激振动的涡激力[18]可表示为
Ft=0.5CLρDU2Lc-
0.5CDρDULc(∂w(x,t)/∂t|x=L+
0.5D∂2w(x,t)/∂x∂t|x=L)
(2)
式中:CL、CD分别是脉动升力和阻力系数,CL=Clq(t)/2、CD=2,其中Cl=0.3为静升力系数,q(t)用来描述圆柱涡街脱落的尾迹运动,其运动方程为
(A/D)(∂w2(x,t)/∂t2|x=L+
(0.5D∂3w(x,t)/∂x∂t2|x=L)
(3)
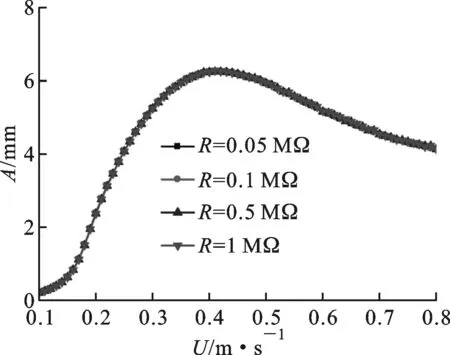
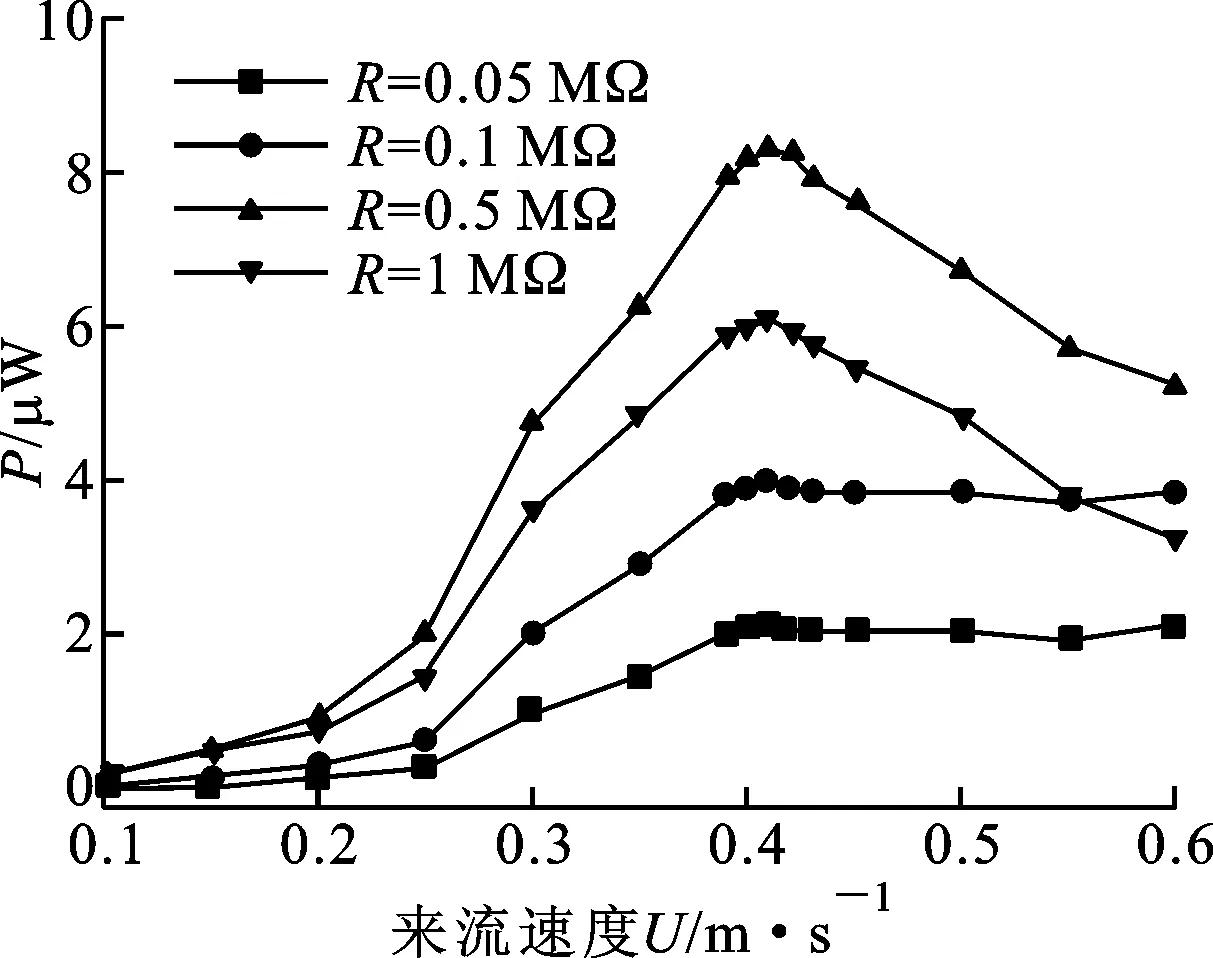
根据Facchinetti的研究[18],λ=1,ε=0.3,A=12,ωf是涡脱频率,ωf=2πStU/D,其中St为斯特劳哈尔数,在雷诺数为300 根据图1b,俘能器可等效为图2所示的电路。 图2 俘能系统的等效耦合电路 根据图2,等效耦合电路方程可写成 (4) 式中:Cp为压电俘能器的等效电容。 俘能系统的输出功率表示为 (5) 式中:T为输出电压的交变周期。 通过联立式(1)~式(5),即可求得俘能系统的输出功率。为了求解耦合方程组式(1)~式(4),根据分离变量法,将位移函数ω(x,t)表示为 φr(x)ηr(t) (6) 式中:φr(x)为r阶的主振型函数;ηr(t)为广义坐标。 压电俘能器的边界条件表示为 w(0,t)=0, ∂w(x,t)/∂x|x=0=0 (7) (8) 式中:M=M0+Mf,M0为圆柱质量,Mf为流体对圆柱和压电梁的附加质量;It为相对于中心的转动惯量,且It=M(D/2)2/2。流体的附加质量[18-19]可表示为 Mf=ρfπD2Lc/4+(33/140)πρfb2(L/4) (9) 悬臂梁的各阶主振型[2]为 φr(x)=Ar[cos(λrx/L)-cosh(λrx/L)+ γr(sin(λrx/L)-sinh(λrx/L)] (10) 式中 (11) Ar为振型系数,满足各阶主振型正则化,具体见文献[2]。 ωr是系统的无阻尼固有频率,可表示为 (12) 式中:λr由式(13)获得 cosλrcoshλr+(λrM/mL)(cosλrsinhλr- sinλrcoshλr)=0 (13) 将式(2)代入式(1),并将式(6)代入式(1)、式(3)和式(4),方程两边同时乘以振型函数φr(x)并沿整个悬臂压电梁长度L积分,然后利用正则振型的正交性简化方程,最后得到对应各阶振型的耦合振动方程组 (14) (15) (16) 式中:χr=θφ′r(L);ζr=csωr/(2K)+ca/(2mωr)。 为了求解式(14)~式(16),引入状态变量 (17) 因此,可将式(14)~式(16)写成 (18) 式中: (19) χrX2n+3+φr(L)(ClρDU2LcX2n+1)/2 (20) 压电片选用型号为MFC-M8514-P2(产自Smart Material Corp®)的压电纤维复合材料,其压电片表面有良好的绝缘作用,可置于水流中进行涡激振动俘能工作。压电俘能器的支撑层选用纯铝材质,圆柱采用尼龙材料制作,并通过自由振动衰减法测量压电俘能系统的一阶阻尼比为ζ1=0.086。 表1 压电俘能器的结构与材料参数 根据表1所给出的参数,通过MATLAB®软件中的ode45求解器求解式(18),根据数值计算结果分析了水流流速和外接电阻对压电俘能器的振动和俘能的影响规律,具体如图3~图6所示。图3给出了在外接电阻为0.5 MΩ,水流速度分别为0.3、0.5和0.7 m/s时,压电俘能器的振动和输出电压情况。由图3可知,压电俘能器在水流的激励下,从静止状态经过几个周期的调整后变为稳定的周期性振动;压电俘能器在不同的流速下振动幅值不同,流速为0.5 m/s时的振动幅值大于流速为0.3和0.7 m/s时的振动幅值,流速为0.7 m/s时的振动频率大于流速为0.3和0.5 m/s时的振动频率,振动频率随流速的增大而增大,如图 3a和图3b所示;由图3c和图3d可知,输出电压与压电俘能器的振动情况有相同的变化趋势,电压变化频率等于振动频率。 图4和图5给出了在外接电阻为0.05、0.1、0.5和1 MΩ时,压电俘能器振动幅值和输出功率随流速的变化情况。由图4可知:外接电阻对压电俘能器的振动幅值影响较小,流速是振动幅值的主要影响因素;振动幅值随流速的增大先增大后减小,在流速为0.41 m/s处达到最大值,此时处于涡激共振区域内;振动幅值达到最大值后,随着流速的增大,振动幅值缓慢降低,频带较宽,有利于压电俘能器的振动俘能。由图5可知,不同外接电阻下,压电俘能器的输出功率随来流速度的变化趋势不同:当外接电阻较小时(例如0.05和0.1 MΩ),输出功率随流速的增大先增大,然后趋于平稳变化;当外接电阻较大时(例如0.5和1 MΩ),输出功率随流速的增大先增大后减小,分别在0.43 m/s处达到最大值。由此可知:较大的外接电阻更适合较低流速环境,而较小的外接电阻则更适合较高流速环境。 图4 不同外接电阻下压电俘能器尾端振动幅值随流速的变化曲线 图5 不同外接电阻下压电俘能器输出功率随流速的变化曲线 为了进一步阐明外接电阻、来流速度和输出功率三者之间的关系,图6给出了在不同的流速情况下输出功率随外接电阻的变化曲线图。由图6可知,在不同的流速下,输出功率都随外接电阻的增大而先增大后减小,存在一个电阻值使压电俘能器的输出功率最大,称之为最优电阻值,且最优电阻值随流速的增大而逐渐减小,这是因为随着流速的增大,压电俘能器的振动频率增大,相应的其最优电阻值逐渐减小,也是在较低流速环境中采用较大的外接电阻,在较高流速情况下采用较小的外接电阻可获得更多的能量输出的原因。 图6 不同流速下输出功率随外接电阻的变化曲线 根据表1中的压电俘能器结构参数设计并制作了实验样机,搭建的涡激振动俘能系统实验平台如图7所示。压电梁悬臂梁在来流前方固定,为了降低夹具对来流的干扰,采用流线型夹具加持。实验台采用水循环系统,主要由水槽、离心水泵、进水管和出水管组成。实验段采用明渠水槽,长度为1 500 mm,宽度为400 mm。实验中,水流深度保持恒定,即水流截面积保持不变,通过调节实验段的倾斜度和流体流量综合控制水流流速。实验段水槽的倾斜度由千斤顶调节;实验段水流流量通过进水管和出水管组合控制。可调电阻器调节外接电阻值大小,并通过示波器显示压电俘能器输出电压值。 图7 涡激振动俘能实验系统图 利用图7所示的涡激振动俘能实验系统,测试了压电俘能器在流速0.1~0.6 m/s范围内,不同外接电阻下的输出功率。图8给出了实验测得压电俘能器在外接电阻为0.05、0.1、0.5和1 MΩ时,输出功率随流速变化的实验结果。 图8 不同外接电阻下实验测得压电俘能器输出功率随流速的变化曲线 由图8可见,当外接电阻为0.05和0.1 MΩ时,输出功率随流速的增大先增大,在流速为0.4 m/s之后随流速的增大而平稳变化;当外接电阻为0.5和1 MΩ时,输出功率随流速的增大先增大后减小,在涡激共振点0.41 m/s处达到最大值,分别为8.3和6.1 μW。对比图5发现,数值分析结果与实验测试结果吻合较好,验证了涡激振动压电俘能系统数学建模的正确性。 本文提出了一种基于水流环境下的涡激振动式压电俘能器,并通过数学建模和实验测试,研究了水流流速和外接电阻对压电俘能器的振动特性和输出功率的影响规律。研究表明:压电俘能器在涡激共振时振动幅值最大,振动频率随流速的增大而增大;输出功率受外接电阻和流速两者的综合影响,较低的流速下采用较大的外接电阻和较高的流速下采用较小的电阻可获得更大的功率输出;压电俘能器在涡激共振时能量输出最大,当外接电阻为0.5 MΩ、流速为0.41 m/s时,实验测试得到了8.3 μW的最大输出功率。数学模型数值计算结果和实验测试结果吻合较好,验证了数学建模的正确性。 [1] 袁江波, 谢涛, 单小彪, 等. 压电俘能技术研究现状综述 [J]. 振动与冲击, 2009, 28(10): 36-42. YUAN Jiangbo, XIE Tao, SHAN Xiaobiao, et al. A review of current situation for piezoelectric energy harvesting [J]. Journal of Vibration and Shock, 2009, 28(10): 36-42. [2] ERTURK A, INMAN D J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations [J]. Smart Materials and Structures, 2009, 18(2): 025009. [3] ERTURK A, INMAN D J. A distributed parameter electromechanical model for cantilevered piezoelectric energy harvesters [J]. Journal of Vibration and Acoustics, 2008, 130(4): 041002. [4] 谢涛, 袁江波, 单小彪, 等. 多悬臂梁压电振子频率分析及发电实验研究 [J]. 西安交通大学学报, 2010, 44(2): 98-101. XIE Tao, YUAN Jiangbo, SHAN Xiaobiao, et al. Frequency analysis and electricity generated by multiple piezoelectric cantilevers in energy harvesting [J]. Journal of Xi’an Jiaotong University, 2010, 44(2): 98-101. [5] 王红艳, 谢涛, 单小彪, 等. 压电悬臂梁俘能器多模态俘能效果研究 [J]. 西安交通大学学报, 2010, 44(6): 114-119. WANG Hongyan, XIE Tao, SHAN Xiaobiao, et al. Multi-mode vibration with piezoelectric cantilever for energy harvesting [J]. Journal of Xi’an Jiaotong University, 2010, 44(6): 114-119. [6] WANG Hongyan, TANG Lihua, SHAN Xiaobiao, et al. Modeling and performance evaluation of a piezoelectric energy harvester with segmented electrodes [J]. Smart Structures and Systems, 2014, 14(2): 247-266. [7] SONG Rujun, SHAN Xiaobiao, LV Fengchi, et al. A study of vortex-induced energy harvesting from water using Pzt piezoelectric cantilever with cylindrical extension [J]. Ceramics International, 2015, 41(S1): S768-S773. [8] SHAN Xiaobiao, SONG Rujun, LIU Bo, et al. Novel energy harvesting: a macro fiber composite piezoelectric energy harvester in the water vortex [J]. Ceramics International, 2015, 41(S1): S763-S767. [9] AKAYDIN H D, ELVIN N, ANDREOPOULOS Y. Energy harvesting from highly unsteady fluid flows using piezoelectric materials [J]. Journal of Intelligent Material Systems and Structures, 2010, 21(13): 1263-1278. [10]AKAYDIN H D, ELVIN N, ANDREOPOULOS Y. Wake of a cylinder: a paradigm for energy harvesting with piezoelectric materials [J]. Experiments in Fluids, 2010, 49(1): 291-304. [11]DAI H L, ABDELKEFI A, WANG L. Piezoelectric energy harvesting from concurrent vortex-induced vibrations and base excitations [J]. Nonlinear Dynamics, 2014, 77(3): 967-981. [12]GAO Xiaotong, SHIH W H, SHIH W Y. Flow energy harvesting using piezoelectric cantilever with cylindrical extension [J]. IEEE Transactions on Industrial Electronics, 2013, 60(3): 1116-1118. [13]MICHELIN S, DOARE O. Energy harvesting efficiency of piezoelectric flags in axial flows [J]. Journal of Fluid Mechanics, 2013, 714(1): 489-504. [15]ABDELKEFI A, YAN Z, HAJJ M R. Modeling and nonlinear analysis of piezoelectric energy harvesting from transverse galloping [J]. Smart Materials and Structures, 2013, 22(2): 025016. [16]SIROHI J, MAHADIK R. Piezoelectric wind energy harvester for low-power sensors [J]. Journal of Intelligent Material Systems and Structures, 2011, 22(18): 2215-2228. [17]ZHAO Liya, TANG Lihua, YANG Yiaowen. Enhanced piezoelectric galloping energy harvesting using 2 degree-of-freedom cut-out cantilever with magnetic interaction [J]. Japanese Journal of Applied Physics, 2014, 53(6): 060302. [18]FACCHINETTI M L, DE LANGRE E, BIOLLEY F. Coupling of structure and wake oscillators in vortex-induced vibrations [J]. Journal of Fluids and Structures, 2004, 19(2): 123-140. [19]BASAK S, RAMAN A, GARIMELLA S V. Hydrodynamic loading of microcantilevers vibrating in viscous fluids [J]. Journal of Applied Physics, 2006, 99(11): 114906. (编辑 武红江) Modeling and Experimental Study of Piezoelectric Energy Harvester under Vortex-Induced Vibration SONG Rujun1,SHAN Xiaobiao1,LI Jinzhe2,XIE Tao1 (1. School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China;2. College of Mechanical and Electrical Engineering, Northeast Forestry University, Harbin 150040, China) A vortex-induced piezoelectric energy harvester (PEH) is proposed to meet the requirement of continuous energy supply for low energy-consumed electronic devices such as MEMS and sensors. The PEH is composed of a piezoelectric cantilever beam and a cylinder and has a simple mechanical structure. The PEH generates vortex-induced resonance at relatively low water velocities and obtains larger output powers. Effects of both the water velocity and the resistance on hydrodynamic response and energy harvesting ability of the PEH are investigated through mathematical modeling and experimental study. It is found that the vibration frequency increases as the velocity increases and the maximum vibration amplitude is found when the vortex-induced resonance appears. The Output power depends on both the water velocity and the resistance. More output power can be achieved through configurations of a smaller resistance with a higher velocity or a larger resistance with a lower velocity. The maximum output power is obtained with vortex-induced resonance. The maximum output power of 8.3 μW is obtained in experimental study with 0.5 MΩ and 0.41 m/s. Furthermore, the results of numerical study are consistent with those of the experimental study well, and the validity of the mathematical model is verified. water flow; vortex-induced vibration; piezoelectric energy harvester; energy harvesting 2015-08-04。 宋汝君(1988—),男,博士生;谢涛(通信作者),男,教授。 基金项目:国家自然科学基金资助项目(50875057);中央高校基本科研业务费专项资金资助项目(HIT.NSRIF.2014059;HIT.KISTP.201412)。 时间:2016-01-07 10.7652/xjtuxb201602010 TN 384;TP211 A 0253-987X(2016)02-0055-06 网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160107.1232.004.html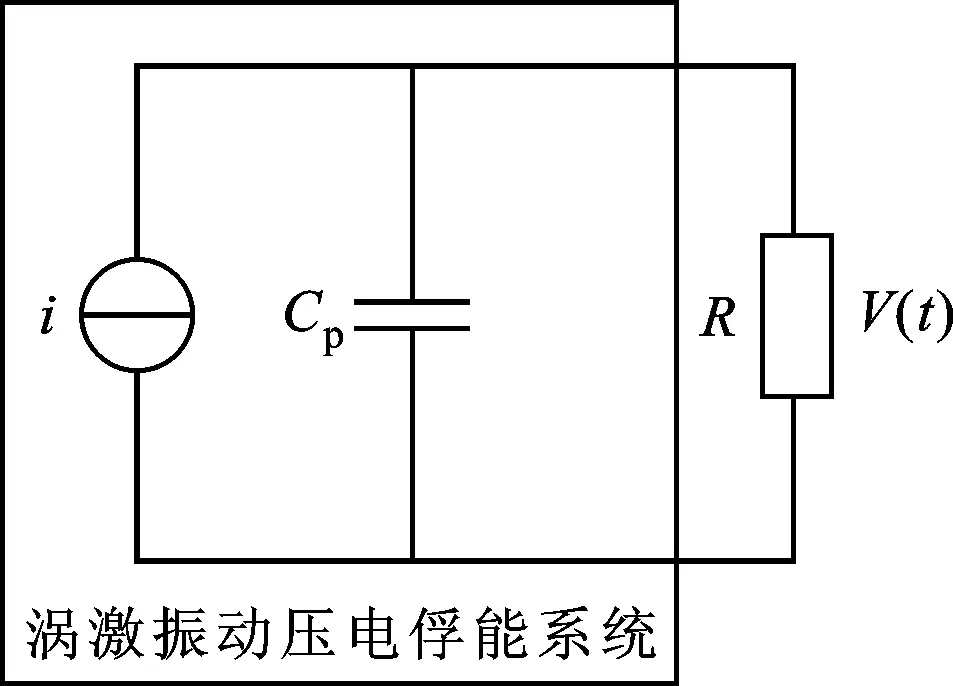
2 非线性数值计算分析



3 实验研究

4 结 论

