考虑应变硬化的混合弹塑性接触模型

王庆朋,张力,尚会超,唐志刚

(重庆大学汽车工程学院, 400044, 重庆)



考虑应变硬化的混合弹塑性接触模型

王庆朋,张力,尚会超,唐志刚

(重庆大学汽车工程学院, 400044, 重庆)

为了更加真实地反映粗糙表面的实际接触情况,根据表面微凸体变化的连续性、单调性和光滑性原理提出了一种新的混合弹塑性接触模型。该模型在球体初始接触时,就考虑更小微凸体的塑性变形和较大变形量时的应变硬化。通过反正切函数构建一组函数,用来表征接触过程中变形状态的变化,利用Meyer硬度指数反映应变硬化的影响,进而导出接触面积和接触载荷的数学表达式。通过采用文献中已有的铜、铝合金和纯镍材料的实验测试结果,以及文献中不同的弹塑性接触模型的计算结果进行对比分析,结果表明,该模型的计算结果能够很好地与实验测试结果吻合,尤其是在大变形量、出现应变硬化的情况下,更能体现出该模型的优势。

微凸体;混合弹塑性;接触模型;应变硬化

粗糙表面对于机械零部件之间结合面的特征参数以及相对运动表面之间的摩擦特性都有重要的影响。为了探究两粗糙表面之间的接触状态,已有很多学者针对这一问题作出了大量的研究。Hertz对接触问题作出了开拓性的研究,提出单个球体弹性接触理论[1];Greenwood等基于这一理论提出经典的粗糙表面和平板之间的接触模型[2];Abbott等首次提出单个球体的完全塑性接触模型(简称AF模型)[3];Pullen等将此模型应用到粗糙表面[4]。然而,上述研究均基于完全弹性或塑性接触理论,显然不符合实际接触情况。为了弥补单一弹性和塑性接触模型的不足,Chang等根据接触区域的体积守恒规律,提出弹性-完全塑性接触模型(简称CEB模型),但是,该模型在屈服点出现接触载荷的跳变[5];Zhao等对CEB模型进行了修正,提出弹性-弹塑性-完全塑性3种变形状态的接触模型(简称ZMC模型)[6]。为了使ZMC模型的弹性区域和完全塑性区域连续、光滑地过渡,赵永武等提出对变形和力之间的关系使用三次函数进行插值[7];类似地,Brake[8]采用Hermite多项式对这一状态进行描述。然而,以上2个函数均属于高阶,这将会导致弹塑性阶段的平均接触压力和法向变形量之间的关系出现振荡。为了解决此问题,徐超等在赵永武模型的基础上,提出一种利用低阶椭圆曲线对弹塑性接触过程进行建模的方法[9];同样地,Brake采用双曲正割函数对这一过程进行表征,并且考虑了接触过程中所产生的应变硬化现象[10]。文献[5-10]所述的模型是基于2个或3个接触状态,但忽略了初始接触时的塑性变形。此外,也有学者采用有限元的方法对球体和平板接触问题进行研究,该方法虽可以精确地描述接触问题,但是,为了反映实际的粗糙特征需要大量的单元网格,而这又需要更多的计算机资源[11-13]。

基于上述研究现状,微凸体的变形包括弹性和塑性2种状态,中间的过渡区域只是两者所占比例不同。对于实际的粗糙表面,正如分形理论所描述的,是有无穷多个微凸体所构成,也就是微凸体上还有微凸体,这就使得两粗糙表面初始接触时,已经有更小尺度的微凸体发生了塑性变形,只是所占的比例较小,而在宏观上表现为弹性变形;当变形量较大时,材料将会表现出应变硬化的现象。为了更加真实地反映实际的接触情况,根据表面微凸体变化的连续性、单调性和光滑性原理,本文提出了一种新的混合弹塑性接触模型。本文模型将弹性和塑性状态扩展到整个接触过程,通过与文献中已有的实验测试结果以及文献中不同的弹塑性接触模型的计算结果进行对比,验证了本文模型的有效性。

1 模型的建立

本文提出的混合弹塑性接触模型是基于以下几个假设条件建立的:

(1)材料是均匀的;

(2)忽略球体之间的摩擦力;

(3)两球体在法向正接触,也就是,未考虑微凸体间的斜碰;

(4)不考虑相邻球体之间的耦合作用。

根据文献[2]的建模方法,2个粗糙表面的接触可以用一个具有等效弹性模量的等效粗糙度表面与一个刚性光滑平面接触来代替,如图1所示。等效弹性模量和半径的计算如下

(1)

(2)

式中:E1、E2、ν1、ν2分别为两接触表面材料的弹性模量和泊松比;r1、r2分别为两接触球体的半径。

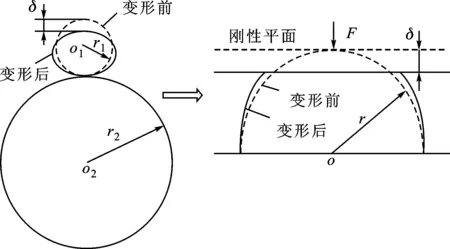
图1 两球体的接触模型及其等效模型

1.1 弹性接触

当变形量较小时,相互作用的球体之间将发生弹性变形。根据经典的Hertz接触理论[1],实际接触面积Ae和平均接触载荷Fe为

Ae=πrδ

(3)

(4)

式中:δ为法向变形量。

关于初始屈服点的计算有很多方法,常见的有2种:一种是Brake采用的,对于两弹性体接触过程中所产生的应力场,根据Von Mises准则来确定材料屈服应力的最大幅值,进而得到初始屈服点的位置[8,10];另一种是通过材料的布氏硬度计算出初始屈服点接触压应力

py=KH

(5)

式中:py为初始屈服点接触压力;K是常量;H为材料的布氏硬度,计算过程中取较软材料的硬度。

有关式(5)中K的取值,在文献[5-10,14-15]中取值范围为0.4～0.6,更多的作者倾向于0.6,在本文模型的计算中K取为0.6。

由式(3)～式(5)可计算出初始屈服点的法向变形量为

(6)

1.2 完全塑性接触

对于完全塑性屈服点的计算,Tabor在研究材料的硬度时,发现初始屈服点和完全屈服点有以下关系[14]

(7)

式中:σy为两接触球体中较软材料的屈服应力,即

σy=min[σy1,σy2]

(8)

对于塑性状态下的平均接触应力,在小的应变硬化条件下,p0≈H≈2.8σy,而对于一般的应变硬化材料,p0≈H≈2.8σf,σf为塑性流动应力,这2种情况都是宏观情况的近似[10]。在微观情况下,有文献发现,这个值是测量值的上限[16],在一些情况下,可以认为布氏硬度的下限为H≈σy[17]。式(7)中p0的计算式为

p0=106H

(9)

完全塑性状态下的接触面积和接触载荷为

Ap=2πrδ

(10)

Fp=p0Ap

(11)

1.3 混合弹塑性接触

当两球体发生接触时,已经有更小尺度的微凸体发生了塑性变形,这时微凸体既存在弹性接触也存在塑性接触。正如文献[7]中所描述的,塑性变形发生在接触面积中心点以下一定深度一个微小的体积内,塑性变形区被体积大得多的弹性变形区所包围,随着变形量的增加,弹性变形所占比例逐渐减小,而塑性变形所占比例随之增大。在初始屈服点和完全塑性屈服点,接触面积和接触压力应该连续和光滑,并且单调增加,不应有突变。

为了表征弹性变形和塑性变形所占比例的变化,构造一组函数

(12)

式中:n为Meyer硬度指数。

f1(δ)、f2(δ)与变形量δ之间的关系如图2所示,该组函数的一些性质如下。

图2 f1(δ)、f2(δ)与变形量δ之间的关系

(1)在初始点,有

(13)

当δ→∞时,有

(14)

由图2可见:对应于f2(δ)的变化,材料的塑性变形所占比例在开始时为0,随着变形量δ的增加而变大,直至无限趋近于1,这时表现为完全塑性变形;f1(δ)的变化对应于弹性变形所占比例的变化。

(2)在定义域(0,+∞),函数的一阶导数为

(15)

从式(15)可知,f1(δ)单调递减,而f2(δ)单调递增,这正好符合两接触球体内部弹塑性状态的变化。

(3)在定义域(0,+∞),函数的二阶导数为

(16)

从式(16)可知,f1(δ)表现为凹的,f2(δ)表现为凸的。在相对较小的变形量下,2种变形状态较快地转换,这主要由材料的初始屈服点、完全塑性屈服点和Meyer硬度指数决定;而当球体处于较大的变形量时,几乎呈现为完全塑性变形,那很小的一部分弹性变形可以解释为:接触表面总有一些相对较小的微凸体处于初始接触状态。

通过以上分析,可以导出接触面积和接触载荷分别为

A=f1(δ)(πrδ)+f2(δ)(2πrδ)

(17)

(18)

2 模型的比较

2.1 模型的无量纲化

为了便于不同模型的比较,有必要进行无量纲化。将模型中的变形量、接触面积和接触载荷分别用初始屈服点处相应的变量进行无量纲化。无量纲化后的接触面积和接触载荷方程分别为

(19)

(20)

式中:δ*为无量纲的变形量。

由于计算模型中忽略了一些影响因素和实验过程中所带来的不确定性,需对f1(δ)和f2(δ)进行略微的修正,修正系数的范围为1±0.05,在以下的单个球体模型验证中,均将f2(δ)乘以1.047。

2.2 铜材料的模型验证及对比

Jamari等通过金刚砂平板对一铜球进行压缩实验[18],测试试件的几何和材料数据如表1所示。

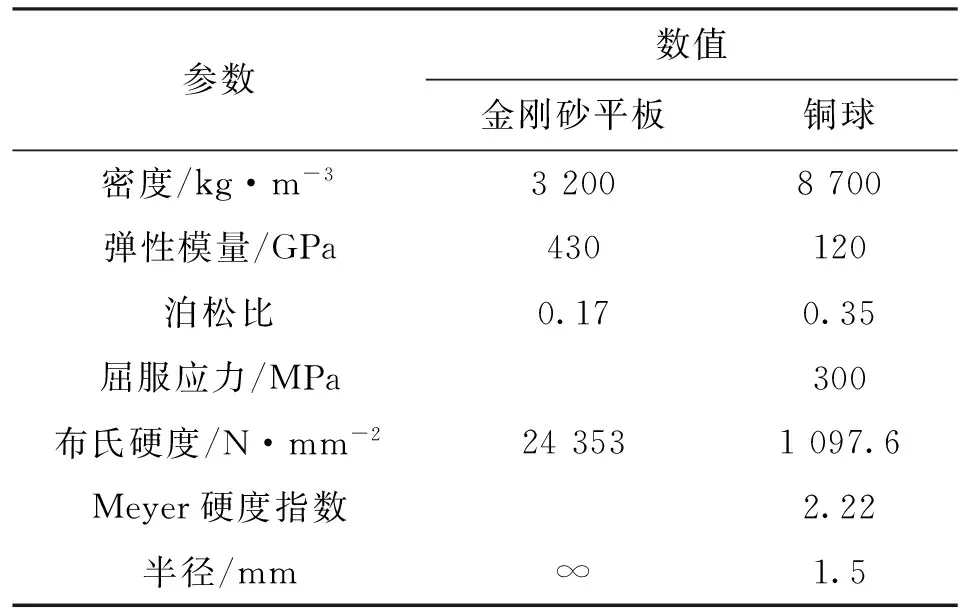
表1 铜球压缩实验中测试试件的参数

本文模型的计算结果和实验测试结果的对比如图3所示。由图3可见,对于变形量-接触面积和接触力-面积曲线,本文模型的计算结果和实验的测试结果能够很好地吻合,尤其对于接触力-面积曲线,应变硬化的影响变得明显。此外,本文模型和文献中的Hertz模型[1]、AF模型[3]、CEB模型[5]、Thornton模型[19]、ZMC模型[6]、Stronge模型[20]、DW模型[21]、Brake2012模型[8]以及Brake2015模型[10]进行对比,结果如图4所示。

从图4a可以看出,10个模型的接触面积和变形量都近似地呈现为线性关系,Hertz、DW和Thornton模型无量纲曲线的斜率均为1,其余模型的无量纲曲线斜率均近似为2。由于Hertz和DW模型没有考虑完全塑性区域,Thornton没有考虑混合弹塑性区域,造成其偏离实验数据。从和实验数据的吻合程度来看,在相对低的变形量下,除了Hertz、Thornton和DW模型,其余7个模型都能较好地吻合。在相对高的变形量下,本文模型的吻合程度最好,其次是ZMC、CEB、AF和Brake2015模型,最后是Stronge和Brake2012模型。

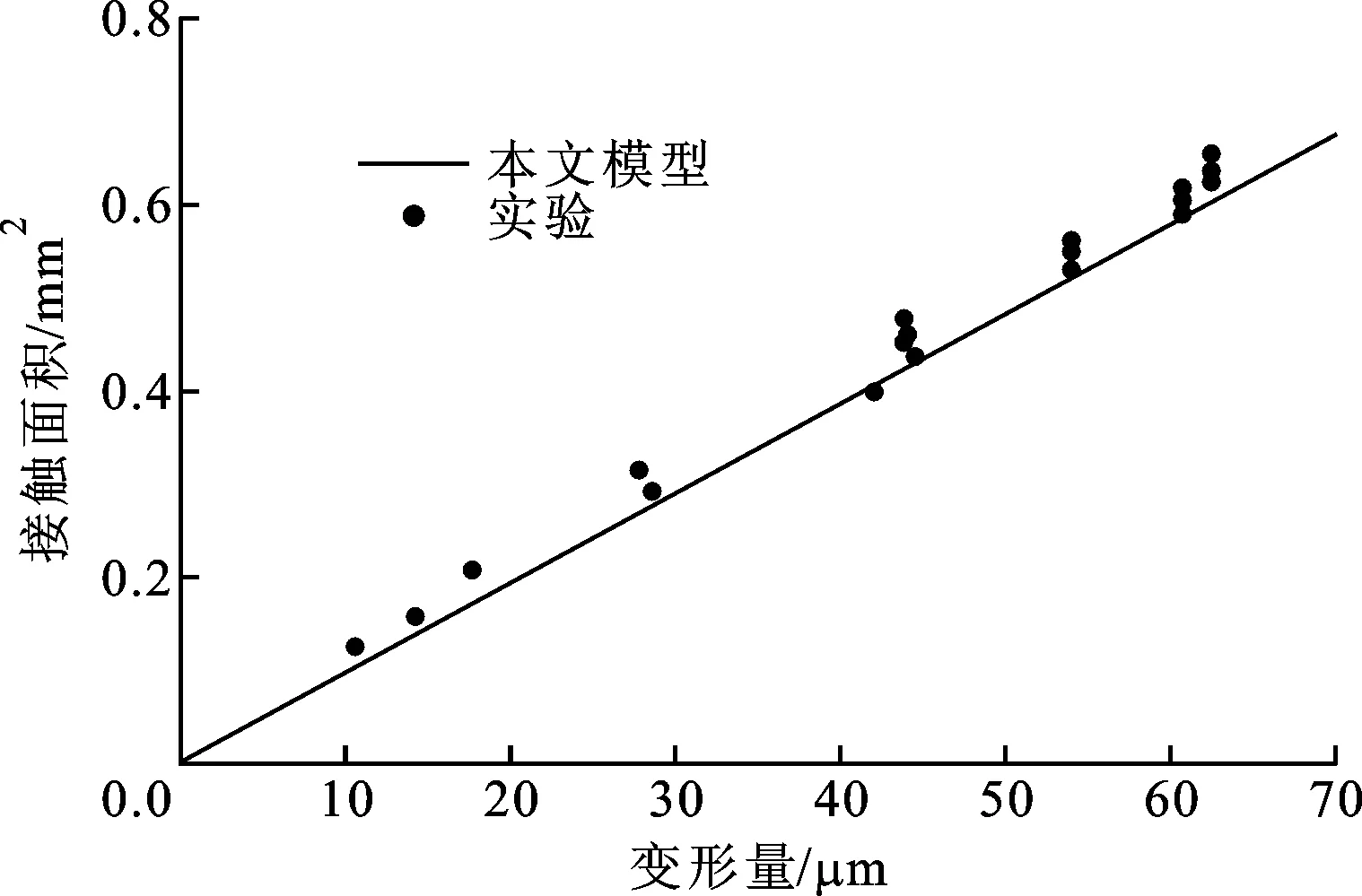
(a)变形量和接触面积

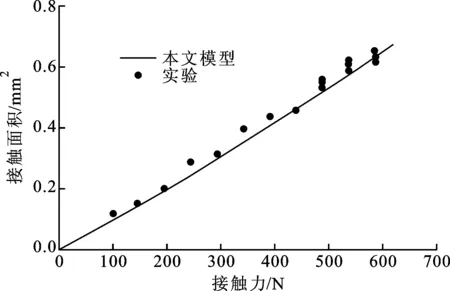
(b)接触力和面积图3 本文模型的计算结果和铜材料实验的结果对比

(a)变形量和接触面积

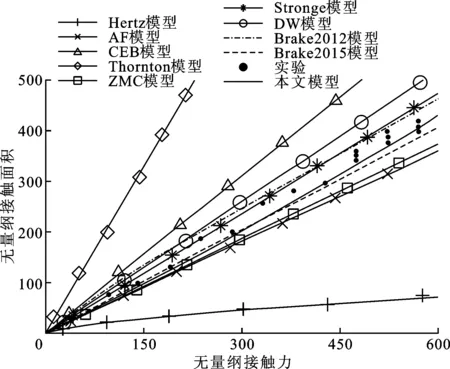
(b)接触力和面积图4 不同模型无量纲曲线和铜材料实验数据对比

从图4b可以看出,不同模型的接触力-面积曲线比较分散,在相对低的接触力下,与实验数据吻合得较好的是本文模型和Brake2012模型,其次是ZMC、AF、Stronge和Brake2015模型,Hertz和Thornton模型则有相对大的偏离。在相对高的接触力下,本文模型表现出明显的优势,有较好的吻合度,其次是Brake2012、Brake2015和Stronge模型,其他模型的吻合程度则相对差一些。

2.3 铝合金材料的模型验证及对比

Jamari等通过金刚砂平板对一铝合金球进行压缩实验[18],测试试件的几何和材料数据如表2所示,铝合金材料在不同模型下的计算结果和实验测试结果对比如图5所示。

表2 铝合金球压缩实验中测试试件的参数

(a)变形量和接触面积

(b)接触力和面积图5 不同模型无量纲曲线和铝合金材料实验数据对比

从图5a可以看出,10个模型的接触面积和变形量同样地都呈现为线性关系,其斜率值和铜材料的情况类似。除了Hertz、Thornton和DW模型,其他7个模型近乎同一条直线,吻合得相当好。从图5b可以看出,对于接触力-面积曲线,表现得比较分散,能够和实验数据吻合得较好的是本文模型和Brake2012模型,其次是Brake2015、AF和CEB模型,其他模型则有较大的偏离。

2.4 镍材料的模型验证及对比

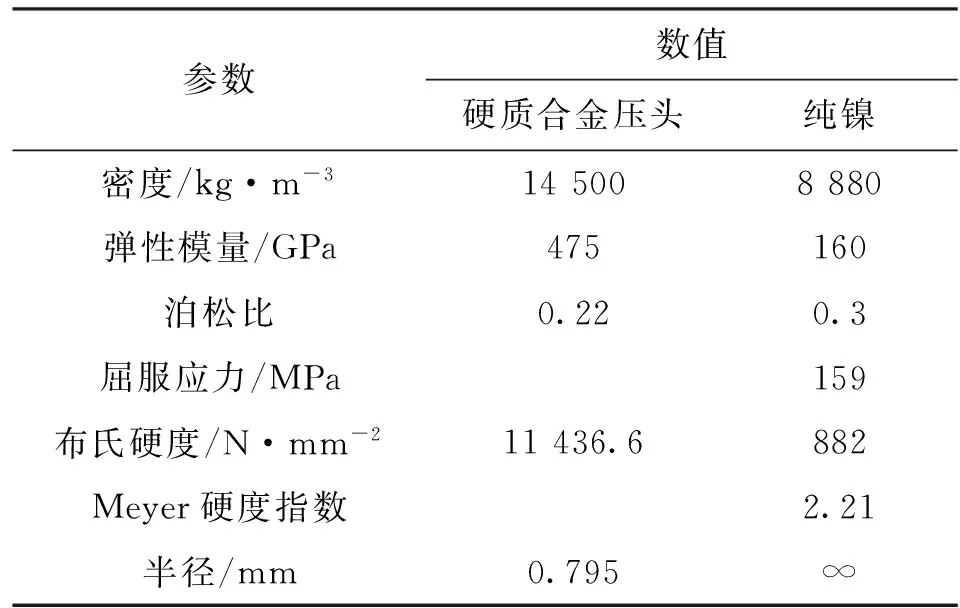
表3 纯镍压缩实验中测试试件的参数

从图6可以看出,对于不同模型的变形量-接触力曲线,相互间的差别较大,能够和实验数据吻合得较好的是Brake2015、Brake2012和本文模型,其他模型的偏差则相对较大。

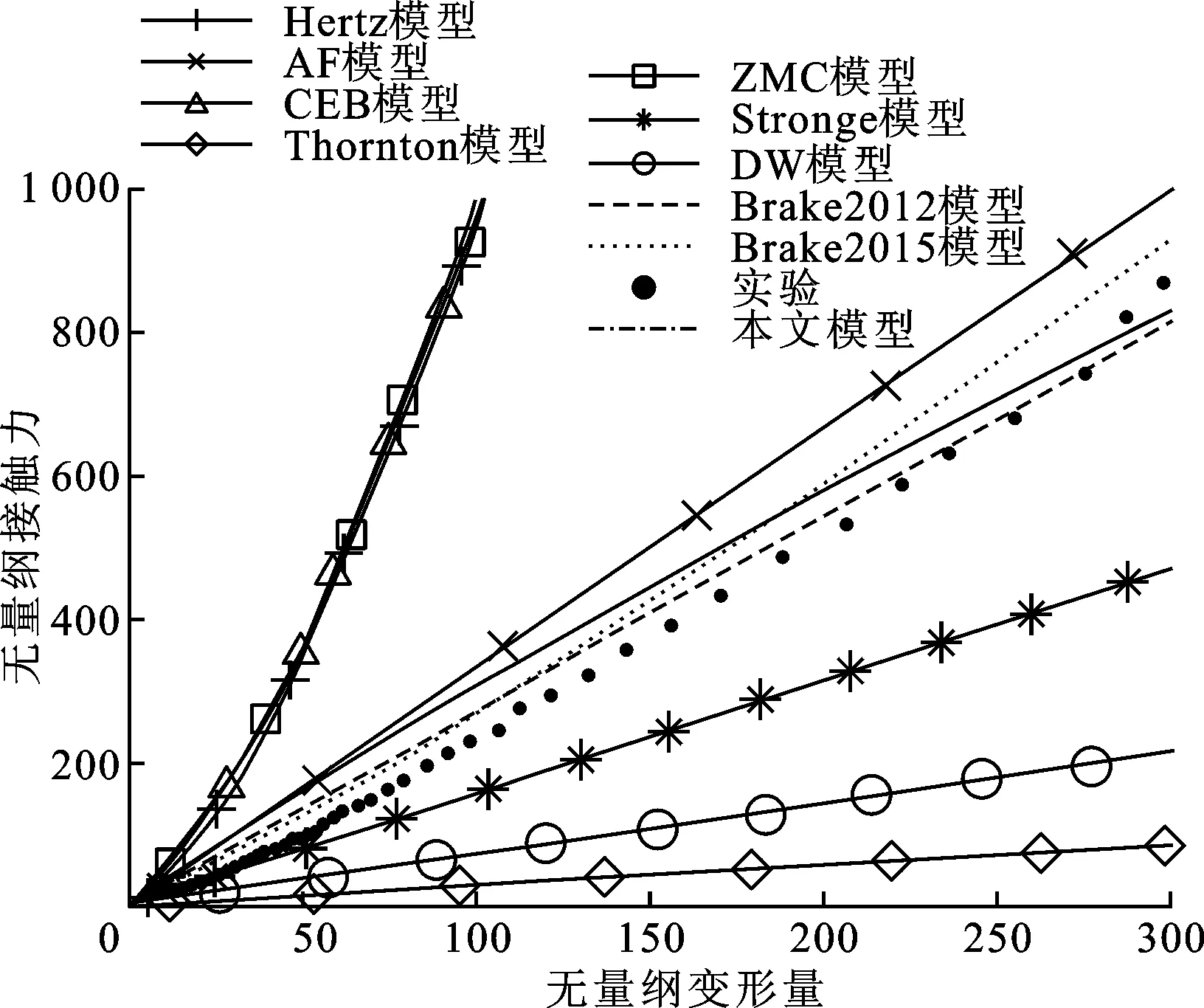
图6 不同模型无量纲曲线和纯镍材料实验数据对比

3 结 论

为了更加真实地反映实际的接触情况,根据表面微凸体的连续性、单调性和光滑性原理提出了一种新的粗糙表面混合弹塑性接触模型。该模型在两球体初始接触时,就考虑更小微凸体的塑性变形,同时,也考虑较大变形量时的应变硬化。

将文献中已有的铜、铝合金和纯镍材料的实验测试结果以及文献中不同的弹塑性接触模型与本文模型的计算结果进行对比,结果表明,本文模型能够较好地和实验数据吻合,尤其是在铜和铝合金材料大变形量的情况下,相对于其他模型更具有优势。

[1] HERTZ H. On the contact of elastic solids [J]. Journal fur die Reine und Andgewandte Mathematic, 1882, 92: 156-171.

[2] GREENWOOD J A, WILLIAMSON J B P. Contact of nominally flat surfaces [J]. Proceedings of the Royal Society of London: Series A, 1966, 295: 300-319.

[3] ABBOTT E J, FIRESTONE F A. Specifying surface quality: a method based on accurate measurement and comparison [J]. Mechanical Engineering, 1933, 55: 569-572.

[4] PULLEN J, WILLIAMSON B P. On the plastic contact of rough surfaces [J]. Proceedings of the Royal Society of London: Series A, 1972, 327: 159-173.

[5] CHANG W R, ETSION I, BOGY D B. An elastic-plastic model for the contact of rough surfaces [J]. ASME Journal of Tribology, 1987, 109(2): 257-263.

[6] ZHAO Y W, MAIETTA D M, CHANG L. An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow [J]. ASME Journal of Tribology, 2000, 122(1): 86-93.

[7] 赵永武, 吕彦明, 蒋建忠. 新的粗糙表面弹塑性接触模型 [J]. 机械工程学报, 2007, 43(3): 95-101. ZHAO Yongwu, LÜ Yanming, JIANG Jianzhong. New elastic-plastic model for the contact of rough surfaces [J]. Journal of Mechanical Engineering, 2007, 43(3): 95-101.

[8] BRAKE M R. An analytical elastic-perfectly plastic contact model [J]. International Journal of Solids and Structures, 2012, 49(22): 3129-3141.

[9] 徐超, 王东. 一种改进的粗糙表面法向弹塑性接触解析模型 [J]. 西安交通大学学报, 2014, 48(11): 115-121. XU Chao, WANG Dong. An improved analytical model for normal elastic-plastic contact of rough surfaces [J]. Journal of Xi’an Jiaotong University, 2014, 48(11): 115-121.

[10]BRAKE M R. An analytical elastic plastic contact model with strain hardening and frictional effects for normal and oblique impacts [J]. International Journal of Solids and Structures, 2015, 62(1): 104-123.

[11]KOGUT L, ETSION I. Elastic-plastic contact analysis of a sphere and a rigid flat [J]. Journal of Applied Mechanics, 2002, 69(5): 657-662.

[12]JACKSON R L, GREEN I. A finite element study of elasto-plastic hemispherical contact against a rigid flat [J]. ASME Journal of Tribology, 2005, 127(2): 343-354.

[13]朱林波, 庄艳, 洪军. 一种考虑侧接触的微凸体弹塑性接触力学模型 [J]. 西安交通大学学报, 2013, 47(11): 48-52. ZHU Linbo, ZHUANG Yan, HONG Jun. Elastic-plastic model for contact of two asperities considering shoulder-shoulder contact [J]. Journal of Xi’an Jiaotong University, 2013, 47(11): 48-52.

[14]TABOR D. The hardness of metals [M]. Oxford, UK: Oxford University Press, 1951.

[15]KOGUT L, ETSION I. A static friction model for elastic-plastic contacting rough surfaces [J]. ASME Journal of Tribology, 2004, 126(1): 34-40.

[16]YU W, BLANCHARD J P. An elastic-plastic indentation model and its solutions [J]. Journal of Materials Research, 1996, 11(9): 2358-2367.

[17]SWADENER J G, GEORGE E P, PHARR G M. The correlation of the indentation size effect measured with indenters of various shapes [J]. Journal of the Mechanics and Physics of Solids, 2002, 50(4): 681-694.

[18]JAMARI J, SCHIPPER D J. Experimental investigation of fully plastic contact of a sphere against a hard flat [J]. ASME Journal of Tribology, 2006, 128(2): 230-235.

[19]THORNTON C. Coefficient of restitution for collinear collisions of elastic perfectly plastic spheres [J]. Journal of Applied Mechanics, 1997, 64(2): 383-386.

[20]STRONGE W J. Impact mechanics [J]. Cambridge, UK: Cambridge University Press, 2000.

[21]DU Y, WANG S. Energy dissipation in normal elastoplastic impact between two spheres [J]. Journal of Applied Mechanics, 2009, 76(6): 1089-1094.

(编辑 刘杨 苗凌)

A Mixed Elastic-Plastic Contact Model Considering Strain Hardening

WANG Qingpeng,ZHANG Li,SHANG Huichao,TANG Zhigang

(College of Automotive Engineering, Chongqing University, Chongqing 400044, China)

A new mixed elastic-plastic model for the real contact is developed to consider both plastic response of smaller asperity and strain hardening effects. It is assumed that the contact behavior is continuous, monotonic and smoothing. An arc-tangent function is used to express different contact status, and the Meyer hardness exponent is used to reflect the effect of strain hardening. Then a math model for both the contact area and the contact load is derived. The proposed model is tested using experimental results for copper, aluminum alloy and nickel reported in the literature, and compared with other contact models in the literature. The proposed model shows a good agreement with experimental results and a big advantage especially when strain hardening occurs.

asperity; mixed elastic-plastic; contact model; strain hardening

2015-06-03。

王庆朋(1987—),男,博士生;张力(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51175530)。

时间:2016-01-12

10.7652/xjtuxb201602022

O343.3

A

0253-987X(2016)02-0132-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160112.1906.002.html