采用多策略离散人工蜂群的改进频谱分配算法

朱冰莲,朱方方,段青言,张良,肖欣庭

(重庆大学通信工程学院, 400044, 重庆)



采用多策略离散人工蜂群的改进频谱分配算法

朱冰莲,朱方方,段青言,张良,肖欣庭

(重庆大学通信工程学院, 400044, 重庆)

针对图论频谱分配模型下最优频谱分配策略搜索解困难、耗时长的问题,提出一种采用多策略离散人工蜂群的频谱分配算法。首先,根据感知技术得到的通信环境状况,建立频谱分配的图论模型;然后,引入多策略离散人工蜂群算法进行最优频谱分配策略的搜索,在搜索初期,引入全局探索能力强的粗搜索策略,以快速优化初始种群,后期以高精度的单维更新进行精细搜索;考虑到仅当解参数值取1才能带来网络收益的增加,提出仅对取值为零的维度进行更新的策略,增强了搜索的有向性与有效性。仿真实验表明:该算法与当前基于离散人工蜂群和二进制粒子算法的频谱分配算法相比,无论是收敛速度还是网络收益都得到提高;当可用频谱数在5～20之间、次用户数量在5～22之间变化时,获得相同最大收益的耗时仅为对比算法的47.75%～36.18%,且随着问题规模增加耗时呈下降趋势。

频谱分配;图论模型;人工蜂群

频谱资源紧张是制约无线通信业务进一步发展的关键性问题之一。然而,大量调查却显示当前频谱利用率极低,如Chiang等对新西兰奥克兰市806～2 750 MHz之间的频段使用情况进行统计分析,结果表明,频谱的有效利用率仅为6.2%[1]。面对这一现象,大量学者指出:并非频谱资源本身短缺,而是当前的频谱管理机制存在严重缺陷[2]。认知无线电技术正是解决这一问题的有效方法[3]。在认知无线电系统下,认知用户可发现未被使用的空闲频谱并智能地接入,这种频谱管理方式极大地提高了频谱利用率[4-5]。实现频谱智能接入的关键技术之一就是实现频谱的合理、高效分配。

在已有的频谱分配模型如图论模型,定价拍卖模型和博弈论模型[6]等中,图论模型通过改变目标效用函数能够满足不同应用场景的需求,且在集中式和分布式等多种频谱管理机制下具有普适性[7],很快成为研究热点。图论模型最初采用图着色算法进行求解,该算法求解速度快,但检测结果差[8]。其后,Zhao等人对模型进行了优化,引入一种映射编码方法,将遗传算法、二进制粒子群算法等新型智能算法引入其中,取得了较好的效果[6]。遗传算法、二进制粒子群算法虽然具有较快的收敛速度,但极易陷入局优。Li等人将离散人工蜂群(discrete artificial bee colony, DABC)用于解决频谱分配问题,提出基于离散人工蜂群的频谱分配(discrete artificial bee colony based spectrum allocation, DABC-SA)算法[9-10],取得了更高的网络收益,但离散人工蜂群算法收敛速度较慢。实时性是认知无线电网络中频谱分配问题不同于其他资源分配问题的显著特点[11],如何在提高网络收益的同时保证收敛速度是关键。受遗传算法、二进制粒子群算法等快速收敛算法的启发,本文提出一种采用多策略引导的多策略离散人工蜂群频谱分配算法(multi-strategy discrete artificial bee colony based spectrum allocation, MDABC-SA)算法,前期引入全局搜索能力强的邻域搜索算子进行粗搜索,以优化初始种群、定位最优解范围,后期改用局部搜索能力强的邻域搜索算子进行细搜索,以保证算法的优化性能,同时有效的先验知识能提高算法搜索效率、促进算法快速收敛。就频谱分配问题而言,增加频谱的分配会导致目标效益函数值的增加,因此,解参数值由0向1的更新才是有效更新,即问题本身存在亲1特性。将亲1特性与优化算法进行融合,保证优化算法搜索的有向性和有效性,进一步加快了收敛速度。

1 基于图论的频谱分配模型

1.1 基本模型

本文采用基于图论的频谱分配模型,并假设信道参数变化相对频谱分配耗时可以忽略。设通信环境中可用频谱数为M,次用户数量为N,信道环境的主要参数如下[7]。

(1)频谱可用性矩阵L={ln,m|ln,m∈{0,1}}N×M,其中ln,m=1表示频谱m对次用户n可用,ln,m=0表示不可用。

(2)效益矩阵B={bn,m|bn,m∈[0,+∞]}N×M,其中bn,m是一个正实数,代表次用户n使用频谱m所能带来的网络收益。

(3)约束矩阵C={cn,k,m|cn,k,m∈{0,1}}N×N×M,可看作M个N×N的二维矩阵,各二维矩阵表示用户在各频谱上的冲突情况,其中cn,k,m=1表示次用户n和次用户k同时使用频谱m会产生干扰,cn,k,m=0时用户n、k可同时在频谱m上通信。显然,当n=k时,cn,k,m的取值由ln,m决定,即cn,k,m=1-ln,m。

(4)分配矩阵A={an,m|an,m∈{0,1}}N×M,它记录了在某一分配周期内,M个频谱对N个认知用户的最终分配策略。an,m=1表示认知用户n可以在该分配周期内使用频谱m,显然,分配矩阵A受约束矩阵C的约束,即当cn,k,m=1时,an,m+ak,m≤1,∀n,k∈[0,N],m∈[0,M]。

根据通信环境需求的不同,网络收益函数有多种不同的形式,在此以平均最大化网络收益总和为目标函数,目标函数的表达式为

(1)

1.2 解的编码

分配矩阵A即为频谱分配的求解对象,直接对A进行编码,则解的维数为N×M,此时解编码的冗余度较高。原因在于:A为受L约束的同维矩阵,L中值为0的元素位置所对应的A中元素值必定为0(不可用频谱必定不能被分配),即当ln,m=0时,an,m=0。因此,文献[6]提出仅对A中对应于L中ln,m=1的an,m进行编码,编码长度D由L中1元素的个数决定,如式(2)表示

(2)

对于一个N=4、M=5的信道环境,直接以A进行编码,长度为20,在二进制空间将有220种不同的A值。用实例来说明解的映射编码原理,如图1所示。图1中,L中有7个1元素,按照文献[6]提供的方法,根据L抽取A中的部分元素进行编码,则解编码X是长度为7的行向量,在二进制空间仅有27不同的值,最优解的搜索范围大大减少。得到最优解X后再按L的抽取关系将X还原成A即可。

图1 解的映射编码实例图

2 基于MDABC的频谱分配算法

2.1 DABC算法

2.1.1 标准ABC算法 人工蜂群算法(artificial bee colony, ABC)是Karaboga模仿自然界蜜蜂觅食行为提出的一种智能优化算法[12]。在ABC算法中,雇佣蜂、守望蜂、食物源在数量上相等,一个食物源位置对应于优化问题的一个解,目标函数的适应度值对应蜂群中食物源的蜜源质量。对于一个D维优化问题,设种群大小为S,则在第t次搜索时,第i个食物源的位置为

(3)

ABC算法主要分为以下3个阶段。

(1)雇佣蜂阶段。雇佣蜂在当前食物源位置附近寻找蜜源质量更高的食物源位置,并将蜜源质量信息传递给守望蜂,雇佣蜂的邻域搜索公式为

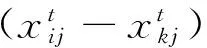
(4)

(2)守望蜂阶段。守望蜂根据雇佣蜂传递的信息,挑选蜜源质量高的食物源进一步开发,以轮盘赌法为各守望蜂选择待采蜜源,并进行邻域开发,守望蜂的邻域搜索公式同式(4)。各食物源被选中的概率与其适应度的大小相关。设pi为第i个食物源被守望蜂选中的概率,则

(5)

式中:fi为第i个食物源的适应度值;fmax、fmin分别为所有食物源中适应度的最大值和最小值。

(3)侦察蜂阶段。当雇佣蜂、守望蜂经过最多U次邻域搜索后,适应度值仍得不到提升的食物源处出现侦察蜂,侦察蜂随机寻找新的食物源替换原食物源位置。U的取值与编码长度D和种群大小S有关,一般取S>D[12]。

2.1.2 DABC算法 ABC算法的解是连续的,不能直接用于离散问题优化。为实现ABC算法向离散域的拓展,Marinakis基于Sigmoid函数离散法提出DABC算法[13],即引入连续域向二进制离散域的映射公式

(6)

2.2 基于MDABC的频谱分配算法

频谱分配问题可描述为:在通信环境参数L、B、C已知的情况下,寻找使目标函数f(A)最大的分配矩阵A。为满足通信实时性要求,本文提出多策略引导的MDABC-SA算法:①根据搜索过程中对算法开发能力和探索能力的平衡要求,引入不同的种群更新策略;②结合频谱分配本身特性,提出在特定维度上进行更新的维度确定策略。

2.2.1 种群更新策略 初始种群的优劣是影响智能算法收敛速度的重要因素[14]。受遗传算法、粒子群算法等全维更新算法启发,在最优解搜索初期,雇佣蜂和守望蜂均采用全维同时更新的搜索策略,以快速优化初始种群,后期保持单维更新的高精度策略,以提高寻优精度。具体方法如下:设置阈值T,当迭代次数t≤T时,进行粗搜索(式(7));当t>T时,进行精细搜索(式(8))

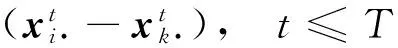
(7)

(8)

阶段的划分是平衡算法探索性能与开发性能[15]的关键。前期的全维更新具有更强的探索能力,但全维更新搜索精度不够,极易陷入局优,该阶段搜索周期过长将阻碍算法的快速收敛,而前期搜索周期过短,又起不到初始解优化的目的。问题规模的大小决定了优化问题的难度,问题规模越大,优化初始解需要的迭代次数越多,故MDABC-SA算法采用与问题规模相关的阶段划分策略。阈值T的确定方法如下式

T=[ξD]

(9)

式中:ξ为初始解优化系数,该参数一般为经验值,取0.08;[·]表示用舍去法取整。

2.2.2 更新维度的选择策略 在基于图论的频谱分配模型中,解的某一维参数由0变为1时意味着系统尝试将某一频带分配给某一认知用户,若分配满足约束矩阵,则目标函数f(A)将会增加由该用户在该频带通信带来的效益值;如分配不满足约束矩阵,则系统根据约束矩阵C随机取消当前某一用户的通信(将存在干扰的2个参数中的1个随机置0)[6]。相反,解的某一维参数由1变为0,虽不会导致干扰冲突,但却意味着让某一用户退出在某一频带上的通信,此时目标函数f(A)必定减小,虽尝试了新的解,但却不是朝着目标函数值增大的方向,此次尝试是无益尝试。尤其是对于单维更新的DABC-SA和MDABC-SA算法中的后期策略,一次只更新一维参数的值,若该维参数的值由1变为0,则必将导致f(A)的值减小,此时尝试的新解必将被淘汰。因此,基于图论的频谱分配模型具有亲1特性,应让新解尝试由0变1。

据此,本文在种群更新策略中加入该先验信息,指引算法更高效地搜索。MDABC-SA算法前期采用全维更新进行粗搜索,引入亲1特性会限制算法的探索能力,导致算法以更大概率地陷入局优,故在算法前期不考虑亲1特性,而在算法后期更注重提高算法的开发能力。后期更新策略和DABC-SA算法一样,采用高精度的单维更新,此时引入亲1特性,选择在当前参数值为0的维度进行更新,更新维度P的确定如下

P=select(j|xi,xij=0)

(10)

式中:操作符select表示随机从向量xi中抽取一取值为0的维度,并将它的维度下标值j返回。

2.2.3 MDABC-SA算法流程 根据上述分析,MDABC-SA算法的一般流程可描述如下。

步骤1 初始化。设置最大迭代次数H、种群大小S、邻域搜索次数最大值U、初始解优化系数ξ,根据式(2)计算编码长度D,由式(9)计算T。随机生成S组形如式(3)的初始蜜源位置x,且x∈{0,1}D,每个蜜源位置x代表一种可能的频谱分配方案。将L中值为1的元素对应的下标(n,m),按先n递增,后m递增的顺序记录在R中,即R={(n,m)|ln,m=1}。

步骤2 干扰约束处理。将所有x按R记录的映射关系映射为A,按C的约束关系进行约束处理[6]:对任意m,查找所有满足cn,k,m=1的(n,k),当an,m和ak,m同时为1时,随机将其中之一置0。将约束处理后的A按R记录的映射关系还原成x。

步骤3 评价各食物源蜜源质量。根据式(1)进行蜜源质量计算,并记录。

步骤4 雇佣蜂阶段。雇佣蜂依次对食物源进行邻域开发:当t≤T时,按式(7)进行更新;当t>T时,由式(10)确定更新维度,再按式(8)进行更新,按式(6)离散化。再按步骤2和步骤3进行约束处理和蜜源质量计算,保留蜜源质量高的食物源。若该蜜源更新,则该蜜源的未更新次数r置0;否则r加1。

步骤5 守望蜂阶段。按式(5)计算各食物源被选中概率,以轮盘赌法为各守望蜂选择待开发蜜源,按步骤4的方法进行邻域开发。

步骤6 侦察蜂阶段。当某蜜源处的r大于U时,该蜜源处出现一只侦察蜂,即随机产生一个形如式(3)的蜜源位置x,且x∈{0,1}D,用x替代旧蜜源位置。

步骤7 停止条件判断。如果迭代次数t小于H,记录S组蜜源中蜜源质量最大的蜜源位置,作为当前最优解,同时,转至步骤4;否则,停止搜索,并将当前最优解按R映射为A,作为得到的最佳频谱分配策略。

2.3 MDABC-SA算法的收敛性分析

文献[16]分析了ABC算法的收敛性,证明了人工蜂群算法是一种全局收敛算法。本文MDABC-SA算法与ABC算法一样,解的更新是一个有记忆的随机游动,当前解仅与上一次迭代解相关,满足有限齐次Markov链的判定条件。MDABC-SA算法与ABC算法的不同在于:MDABC-SA算法引入多策略机制,在搜索初期以全维更新算子进行搜索,以优化初始解,但是全维更新算子仅执行有限次,且MDABC-SA算法的任一策略均保留了贪婪选择策略,在经历足够迭代次数后,这一过程与ABC算法的过程保持一致。因此,MDABC-SA算法也是一种全局收敛的算法。

3 仿真实验与分析

通信环境参数L、B、C,频谱数M以及用户数N设置如下[10]:L为随机生成的0、1矩阵;B中元素取值从1到10中随机选取;C中各二维矩阵为随机生成的0、1对称阵;M=22;N=20。

为分析MDABC-SA算法的性能,将MDABC-SA算法与基于粒子群的频谱分配(BPSO-SA)算法[6]和DABC-SA算法[10]进行比较。参数设置如下:S=20;T=[0.08D];U=SD,H取为500。为了排除偶然性,下面给出的实验结果均为30次仿真的平均结果。

3.1 策略更换阈值T的测试

T的大小关系着算法探索性能和开发性能的平衡,以迭代次数为横轴,平均最大化网络收益总和(以下简称平均收益率)为纵轴,对不同T值进行仿真对比实验,结果如图2所示。图2中,曲线1的T=0,即为DABC-SA算法,收敛速度较慢;当T值过大时,如图中曲线3,算法虽也能收敛,但由于第一阶段过长,停留于局部最优时间过长,从而导致算法收敛速度变慢;而当T取无穷大,即整个搜索过程采用全维更新时,算法无法跳出局优。实验中发现当T取[0.05D]～[0.1D]时,收敛较快,图2中2号线是T取[0.08D]的结果。

图2 不同阈值T时的算法性能

3.2 不同算法下的平均收益

为比较不同策略对收益的影响,分别将引入和未引入更新维度选择策略的情况称为MDABC-SA算法和MDABC0-SA算法。以平均收益为目标函数,MDABC0-SA、MDABC-SA、DABC-SA和BPSO-SA算法的收敛曲线如图3所示。由图3可以看出,DABC-SA算法能够获得较高收益,但收敛性能不如BPSO-SA算法,而MDABC0-SA、MDABC-SA算法的收敛速度都明显快于DABC-SA、BPSO-SA算法,说明初期的种群优化策略是有效的,且MDABC-SA算法无论收敛速度还是优化性能,都优于MDABC0-SA算法,说明亲1特性是有效的先验知识,融入到更新维度的选择策略能够使搜索更具有向性和有效性。

图3 不同算法下网络平均收益率与迭代次数的关系

以计算时间为横轴,得到与图3相对应的收敛曲线如图4所示。由图4可以看出,无论在前期还是后期,达到相同的收益时MDABC-SA算法所需要的计算时间更短。

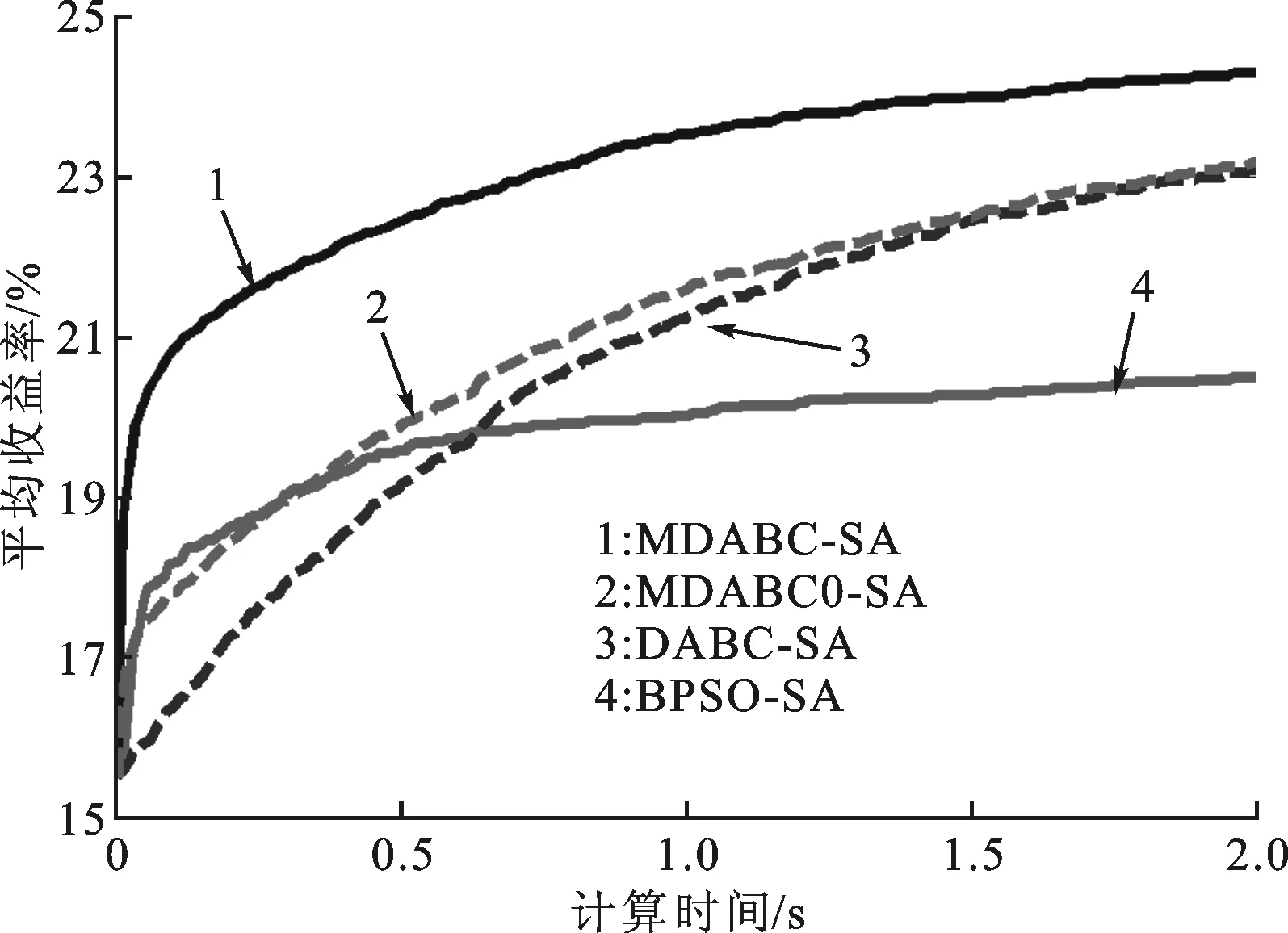
图4 不同算法下网络平均收益率与计算时间的关系

3.3 算法的耗时分析

几种算法达到DABC-SA算法的最大收益值的耗时情况如表1所示。虽然BPSO-SA算法前期具有较快的寻优能力,但易陷入局优,达不到DABC-SA算法的最大收益值,故未在表1中列出。从表1中可以看出:MDABC-SA算法相对于DABC-SA算法耗时大幅减小;当可用频谱数在5～20之间变化、次用户数量在5～22之间变化时,获得DABC-SA算法所能得到的最大收益的耗时仅为其47.75%～36.18%,且随着问题规模增大,耗时比呈现下降的趋势。

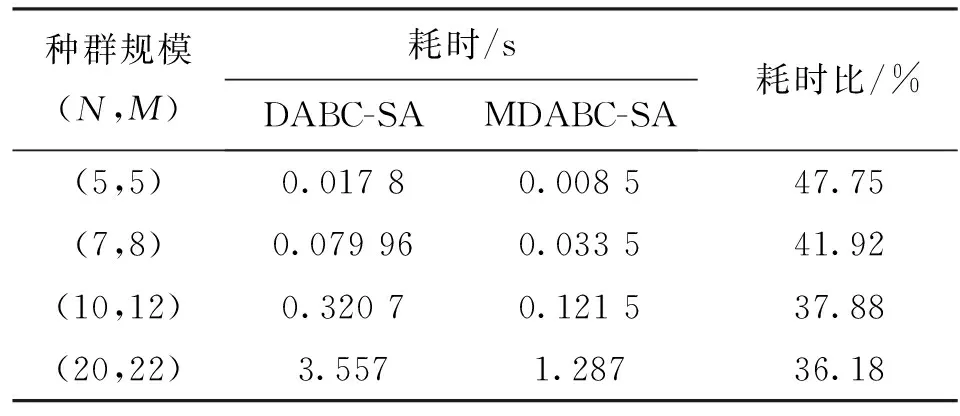
表1 不同算法下的耗时随问题规模变化

注:耗时比为DABC-SA算法的耗时与MDABC-SA算法的耗时之比。

3.4 认知用户数变化下的平均收益

保持可用频谱数M=30不变,改变认知用户数,得到平均收益率随认知用户数N的变化曲线如图5所示,可以看出,随着认知用户数的不断增加,平均收益呈递减变化,MDABC-SA算法始终能获得高于DABC-SA和BPSO-SA算法的平均收益率。

图5 平均收益率随认知用户数的变化关系

3.5 频谱数变化下的平均收益

设认知用户数N=20不变,当可用频谱数M改变时,平均收益率变化曲线如图6所示。由图6可见,随着可用频谱数的增加,平均收益率不断增加,且MDABC-SA算法始终能获得高于DABC-SA和BPSO-SA算法的平均收益率。

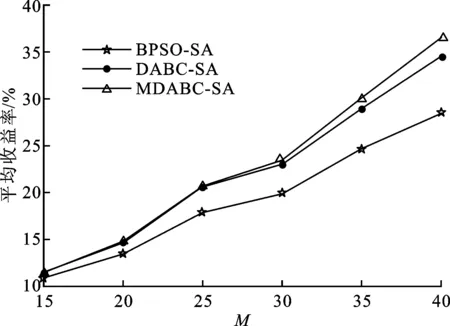
图6 平均收益率随可用频谱数的变化关系

4 结 论

频谱的合理、高效分配是实现认知无线电技术的关键。基于图论的频谱分配模型是一个典型的NP-Hard优化问题,适合用智能算法解决。本文提出的多策略离散人工蜂群频谱分配算法从两方面进行了改进:①引入多策略种群更新机制,在前期采用全维更新策略快速粗搜索以优化初始种群,后期采用单维更新策略进行精细搜索以保证搜索精度;②利用频谱分配问题中存在的亲1特性,提出考虑亲1特性的更新维度选择策略,加强了搜索的有向性与有效性。仿真实验表明,采用多策略离散人工蜂群的频谱分配算法,能够取得更高的网络收益和更快的收敛速度。

[1] CHIANG R I, ROWE G B, SOWERBY K W. A quantitative analysis of spectral occupancy measurements for cognitive radio [C]∥ Proceedings of the IEEE 65th Vehicular Technology Conference. Piscataway, NJ, USA: IEEE, 2007: 3016-3020.

[2] 陈鹏, 邱乐德, 王宇. 卫星认知无线电检测门限与功率分配联合优化算法 [J]. 西安交通大学学报, 2013, 47(6): 31-36, 43. CHEN Peng, QIU Lede, WANG Yu. Joint optimization algorithm of detection threshold and power allocation for satellite underlay cognitive radio [J]. Journal of Xi’an Jiaotong University, 2013, 47(6): 31-36, 43.

[3] 李晓艳, 张海林, 郭超平, 等. 一种异步的认知无线电网络跳频算法 [J]. 西安交通大学学报, 2012, 46(12): 30-35. LI Xiaoyan, ZHANG Hailin, GUO Chaoping, et al. Asynchronous channel hopping algorithm for cognitive radio networks [J]. Journal of Xi’an Jiaotong University, 2012, 46(12): 30-35.

[4] 王兵, 白智全, 董培浩, 等. 采用空时分组编码的动态分组加权合作频谱感知方案 [J]. 西安交通大学学报, 2014, 48(8): 23-28. WANG Bing, BAI Zhiquan, DONG Peihao, et al. A spectrum sensing scheme with weighted collaboration of dynamical clustering using space-time block code [J]. Journal of Xi’an Jiaotong University, 2014, 48(8): 23-28.

[5] TRAGOS E Z, ZEADALLY S, FRAGKIADAKIS A G, et al. Spectrum assignment in cognitive radio networks: a comprehensive survey [J]. IEEE Communications Surveys & Tutorials, 2013, 15(3): 1108-1135.

[6] ZHAO Z, PENG Z, ZHENG S, et al. Cognitive radio spectrum allocation using evolutionary algorithms [J]. IEEE Transactions on Wireless Communications, 2009, 8(9): 4421-4425.

[7] PENG C, ZHENG H, ZHAO B Y. Utilization and fairness in spectrum assignment for opportunistic spectrum access [J]. Mobile Networks and Applications, 2006, 11(4): 555-576.

[8] FRAGKIADAKIS A G, TRAGOS E Z, ASKOXYLAKIS I G. A survey on security threats and detection techniques in cognitive radio networks [J]. IEEE Communications Surveys & Tutorials, 2013, 15(3): 428-445.

[9] GHASEMI A, MASNADI-SHIRAZI M A, BIGUESH M, et al. Spectrum allocation based on artificial bee colony in cognitive radio networks [C]∥ Proceedings of 2012 Sixth International Symposium on Telecommunications. Piscataway, NJ, USA: IEEE, 2012: 182-187.

[10]李鑫滨, 刘磊, 马锴. 基于离散人工蜂群算法的认知无线电频谱分配 [J]. 系统工程与电子技术, 2012, 34(10): 2136-2141. LI Xinbin, LIU Lei, MA Kai. Cognitive radio spectrum allocation based on discrete artificial bee colony algorithm [J]. Systems Engineering and Electronics, 2012, 34(10): 2136-2141.

[11]NAEEM M, ANPALAGAN A, JASEEEMUDDIN M, et al. Resource allocation techniques in cooperative cognitive radio networks [J]. IEEE Communications Surveys & Tutorials, 2014, 16(3): 729-744.

[12]KARABOGA D, BASTURK B. On the performance of artificial bee colony (ABC) algorithm [J]. Applied Soft Computing, 2008, 8(1): 687-697.

[13]MARINAKIS Y, MARINAKI M, MATSATSINIS N. A hybrid discrete artificial bee colony-GRASP algorithm for clustering [C]∥ Proceedings of International Conference on Computers & Industrial Engineering. Piscataway, NJ, USA: IEEE, 2009: 548-553.

[14]GAO W, LIU S, HUANG L. A global best artificial bee colony algorithm for global optimization [J]. Journal of Computational and Applied Mathematics, 2012, 236(11): 2741-2753.

[15]CREPINSEK M, LIU S, MERNIK M. Exploration and exploitation in evolutionary algorithms: a survey [J]. ACM Computing Surveys, 2013, 45(3): 35-38.

[16]宁爱平, 张雪英. 人工蜂群算法的收敛性分析 [J]. 控制与决策, 2013(10): 1554-1558. NING Aiping, ZHANG Xueying. Convergence analysis of artificial bee colony algorithm [J]. Control and Decision, 2013(10): 1554-1558.

(编辑 刘杨)

An Improved Spectrum Allocation Algorithm Using Multi-Strategy Discrete Artificial Bee Colony Technology

ZHU Binglian,ZHU Fangfang,DUAN Qingyan,ZHANG Liang,XIAO Xinting

(College of Communication Engineering, Chongqing University, Chongqing 400044, China)

An improved spectrum allocation (MDABC-SA) algorithm using the multi-strategy discrete artificial bee colony technology is proposed to reduce computational time of spectrum allocation based on graph model. First, a spectrum allocation model is established based on parameters obtained by sensing technology. Then, the multi-strategy discrete artificial bee colony technology is employed to find the optimal spectrum allocation scheme, and a global searching operator is used in initial searches to rapidly find a better initial population, An one-dimensional search is then used in later searches to perform fine line search. The strategy to update only the elements with value of 0 is proposed to inhance the direction and effectiveness of searches by considering the fact that the more ‘1’ have in the solution, the higher network utilization can be achieved. Simulation results and comparisons with the spectrum allocation algorithms using DABC and BPSO algorithms show that the proposed algorithm obviously improves both the convergence speed and network utilization. The algorithm achieves the same maximum benefit with only 47.75%-36.18% of consumed time of the former two algorithms when the number of available spectrum is between 5 and 20 and the number of secondary users varies from 5 to 22 and a downward trend in consumed time is observed when the problem scale increases.

artificial bee colony; spectrum allocation; graph model

2015-04-13。

朱冰莲(1959—),女,教授。 基金项目:国家自然科学基金资助项目(61201177)。

时间:2016-01-03

10.7652/xjtuxb201602004

TP18;TN925

A

0253-987X(2016)02-0020-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160103.2006.002.html