复杂电磁边界下基于曲线坐标的保角变换法
张婧思,苗英恺,刘晓波,张安学
(1.西安交通大学电子与信息工程学院, 710049, 西安;2.濮阳职业技术学院, 457000, 河南濮阳)
复杂电磁边界下基于曲线坐标的保角变换法
张婧思1,苗英恺2,刘晓波1,张安学1
(1.西安交通大学电子与信息工程学院, 710049, 西安;2.濮阳职业技术学院, 457000, 河南濮阳)
针对具有复杂几何边界条件的二维均匀微波传输线中电磁场难以解析求解从而造成其设计困难的问题,提出了一种基于曲线坐标的保角变换法(CMM)。该方法基于二维传输线的横电磁场(TEM)模型。首先利用保角变换将复杂传输线的边界曲线映射为简单传输线的边界曲线,建立复杂边界传输线的曲线坐标;然后利用曲线坐标把复杂边界传输线所满足的麦克斯韦方程转换到简单边界传输线中,形成两种传输线间的电磁映射;最后论证了两种传输线间电荷、电位分别对应相等,由此得到了与传输特性紧密相关的复杂传输线的电容,进而用以指导传输线的设计。由于以电位为中间量的传统保角变换计算较为复杂,采用CMM方法直接从场出发,省去了关于电位的中间计算过程,简化了计算过程。仿真结果表明,不同尺寸下同轴线特征阻抗仿真值与理论值吻合得很好,验证了CMM方法的正确性。
微波传输线;曲线坐标;保角变换;麦克斯韦方程
在微波工程中,二维均匀微波传输线是许多微波电路实现的基础。然而,对于各种边界复杂、性能迥异的非常规传输线,直接求解其电磁场的麦克斯韦方程却几乎难以实现。因此,精确分析与综合设计这些微波传输线已成了相关人员面临的迫切问题。
目前对于此问题的研究主要分为数值法和解析法。数值法是伴随着近些年计算机技术的发展而活跃起来的,主要有时域有限差分法(FDTD)[1]、矩量法[2]等。FDTD基于麦克斯韦方程的时域差分形式,其优点是适合于宽带计算,计算时间短,但缺点是难以计算电大尺寸物体,对计算机性能要求比较高;矩量法基于电磁场的变分原理,通过选择一组基函数去近似真实的场分布,优点是过程简单,求解步骤统一,应用起来比较方便,但缺点是需要一定的数学技巧,如基函数与权函数的选取,同时为了达到所需要的计算精度,矩量法的计算任务也很繁重。解析法则主要有直接法、变分法[3]等。直接法即是求解电磁场所满足的麦克斯韦方程,但这种方法由于边界过于复杂,一般很少采用;变分法是建立某些参量的稳定泛函,从而获得该参量的解析闭式,其结果对于器件的综合设计可以提供较好的指导作用,缺点是闭式的精度难以保证,与试探函数的选取有重要关系。此外,部分学者[4]尝试利用近些年发展起来的变换光学[5]解决此类问题,通过坐标变换将复杂边界变换为规则边界,而其他方法则一般需要在变换区域填充复杂介质,最后再利用数值方法进行求解,因此可以算是一种半解析半数值的方法,虽由此降低了计算的难度,但缺点是仍不能获得解析闭式。因此,问题的关键在既能较精确地分析器件场分布,又能获得一些参量较精确的解析闭式,用以指导器件的综合设计。
针对以上问题,本文提出了一种基于曲线坐标的保角变换(CMM)方法。首先,对于复杂传输线的的几何边界,总可以通过直线逼近,建立适当的保角变换,将其变换为简单传输线的几何边界;其次,保角变换法可以得到精确的解析结果,这对于器件的综合设计具有重要意义;此外,对于传统方法较难解决的性能迥异的非常规传输线问题,采用CMM方法可以直接从场出发,省去关于电位的中间计算过程,在保证计算精度的同时,可有效节约计算资源。
1 理论模型
对于微波工程中具有复杂几何边界条件的二维传输线,分析传输线的场分布是传输线综合设计的第一步,之后再利用分析结果指导传输线的设计。
首先,利用保角变换法求解复杂几何边界条件的二维传输线,以最简单的圆同轴为例进行讨论。同轴线截面和平行板截面模型如图1所示,已知真空中圆同轴内外半径分别为a、b。该同轴线几何边界作保角变换映射为一有限长度平行线(平行板),映射关系如下
(1)
式中:(x,y)为同轴线系统的直角坐标;(u,v)为同轴线系统的曲线坐标,同时也是平行板系统中的直角坐标。
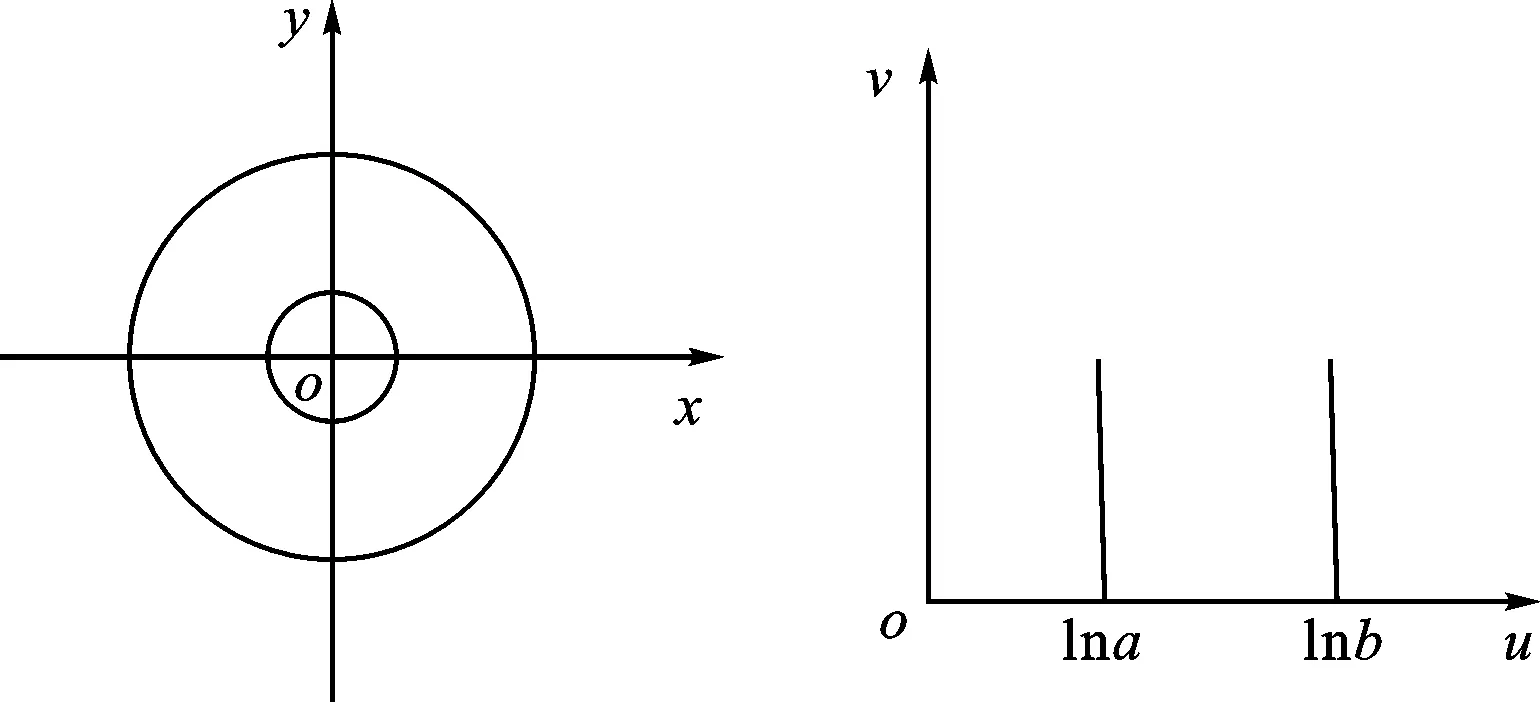
(a)同轴线截面 (b)平行板截面图1 同轴线截面和平行板截面
为了分析同轴线中的场分布,首先假设同轴线中的场在直角坐标系(x,y)中为如下形式
(2)
公式满足真空中的麦克斯韦方程,式中Ex、Ey、Bx、By为同轴线中的电场和磁场在直角坐标系(x,y)下的直角分量。
其次,为了建立同轴线与平行板中的场分布的映射关系,将上述同轴线中的场分布式(2)改写在曲线坐标系(u,v)中,此时有下式成立
(3)
式中:Eu、Ev、Bu、Bv是同轴线中的场分布在曲线坐标系下的逆变分量,与直角分量存在如下关系
(4)
最后,将同轴线中的场分布代入真空中的麦克斯韦方程,并将其表示在曲线坐标系(u,v)中,具体形式如下
(5)
式中:ρ1是电荷密度;j1是电流密度;g1/2是保角变换度规矩阵的行列式;Eu、Ev、Bu、Bv是同轴线中的场分布在曲线坐标系下的协变分量,其中,Eu和场的逆变分量Eu存在关系Eu=g1/2Eu
通过上述分析可以发现,式(5)恰为平行板中直角坐标(u,v)的场分布所满足的二维麦克斯韦方程组。因此,可以得出平行板中的场源如下
(6)
至此,在保角变换的约束下,利用曲线坐标从麦克斯韦方程出发,建立了变换前后两种传输线间的电磁映射关系,即同轴线中的场源总是可以用平行板中的场源进行表示。
2 电容的计算
对于二维均匀微波传输线而言,可以通过场的方法(场模型)进行求解分析。由于二维均匀微波传输线一般涉及横电磁场(TEM),因此可以建立更为简单有效的电路模型,其中电路参数由场分布决定。对于传输线的电路模型而言,与其传输特性紧密相关的常数如衰减常数[6]和特征阻抗[7-11]都可以利用电容求得,而电容是与传输线的尺寸相关。因此,电容对于传输线的指导设计具有重要意义。
考虑到电容定义C=Q/V,其中Q为单位长度传输线的电荷,V为传输线两导体间的电压,因此可以利用CMM方法建立单位长度同轴线与平行板间电荷、电位的数学关系,从而得出两传输线间的电容关系。
2.1 电荷的变换关系
为了求解两传输线间的电荷关系,首先考虑变换前后两传输线对应的微小体积元中电荷的关系,对于两者间对应的任意微小体积元存在数学关系dxdy=g1/2du1du2,再利用变换前后两传输线电荷密度的关系式(6)求解。可以论证:保角变换导致了传输线体积的变化和电荷密度的反比例变化,从而保证了电荷的变换相等。变换关系式如下
(7)
式中:dQ1是同轴线系统单位积元中的电荷;dQ2是平行板系统单位体积元中的电荷。
除此之外,还可以验证同轴系统中的电流连续性方程映射为平行板系统中的连续性方程,从侧面说明了映射后平行板系统中的电荷与电流之间是自洽的,没有违背基本的电荷守恒定律。在同轴线中,电流连续性方程如下
(8)
如果将式(8)用同轴系统中的曲线坐标系(u,v)表示,则有
(9)
显然,式(9)恰为平行板系统中的电流连续性方程。至此得到了保角变换前后,单位长度同轴与平行板电荷之间变换相等,同时也验证了映射后的平行板系统具有自洽性。
2.2 电位的变换关系
对于二维均匀传输线,由于其一般涉及TEM场,而此电场是梯度场,因此可以定义任意两点间的电压如下
V=∫E·dr
(10)
利用式(10),可以计算同轴线中任意两点间的电位差V1与平行板中对应两点间的电位差V2之间的关系。V1与V2的表达式如下
V1=∫Exdx+∫Eydy
(11)
V2=∫Eudu+∫Evdv
(12)
为论证V2与V1的关系,可以把V2表达式中的参量Eu、u等用同轴系统中的直角参量Ex、x等表示,并考虑到保角变换的柯西-黎曼条件,可将上式化简如下
(13)
最后,只需要利用下述雅可比行列式关系,就可化简式(13),建立起V2与V1的关系
(14)
计算可得
(15)
将式(15)代入式(13)可得
V2=∫Exdx+∫Eydy
(16)
至此,从上式可以得出结论:同轴系统中任意两点与平行板系统中对应两点的电位差保持不变。
从电容的基本定义出发,根据两传输线间的电荷和电位的变换关系可以得出:单位长度的同轴与平行板电容相等,即保角变换具有保电容性。这与之前的研究结论[12]是一致的。
对于工程实际所需要的传输线,可以从传输线参量如特征阻抗、衰减常数出发,求得传输线的电容,最后再利用电容,求得传输线相应的尺寸。
2.3 算例验证
为了验证本文CMM方法的有效性,具体计算同轴线场分布及电容值。
首先,利用式(4)建立同轴系统场的直角分量与其在(u,v)曲线坐标下的协变分量Eu、Ev之间的关系如下
(17)
其次,由于同轴线关于角度是周期的,因此在(u,v)直角平面可无限延伸,故而在平行板系统中,Eu、Ev作为平行板场的直角分量满足下式
(18)
然后,在已知平行板电场分布Eu、Ev的前提下,将式(18)代入式(17),即可得出同轴线场的直角分量Ex、Ey
(19)
(20)
则电场矢量可表示为
(21)
至此,即通过曲线坐标法,利用平行板的场分布反演出了同轴线的场分布。从上述过程可清晰看到,在平行板逐渐弯曲为同轴线过程中,平行板中的电场也在逐渐的扩散,以适应边界。可以验证,式(21)与参考文献[13]中的相应公式是一致的。
最后,利用已求得的场分布,计算同轴导体内外的电压和电荷。单位长度同轴线与平行板上电荷为
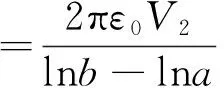
(22)
(23)
同样,利用电压定义,可求得同轴内外导体间的电压如下
(24)
式(22)~式(24)与第2节中关于电荷电压的结论一致,从而验证了本文方法的正确性。利用电容定义即可求得单位长度同轴线的电容
(25)
考虑到工程实际需求,由电容即可求得同轴线的关键参量特征阻抗
(26)
利用CMM方法计算了同轴线的场分布及电容等参量,结论与之前的理论分析一致。对于工程实际所需要的传输线,可以从其传输线参量如特征阻抗出发,求得传输线的电容,再利用电容求得传输线相应的尺寸,完成设计过程。
2.4 仿真验证
利用商业软件CST2013可仿真得出不同尺寸下同轴线的特征阻抗。设置工作频率为3 GHz,内半径a=1 mm,导体具有理想电边界,内外导体中间填充空气。表1给出了在上述仿真条件下,不同外半径时同轴特征阻抗的仿真结果与理论结果。
从表1中可以看出,在不同尺寸下,同轴特征阻抗理论值与数值仿真结果吻合得很好,从而说明了本文CMM方法的正确性。

表1 不同外半径下同轴特征阻抗
3 结 论
本文针对复杂边界条件下的二维均匀传输线中电磁场难以解析求解从而造成设计困难的问题,提出了一种基于曲线坐标的保角变换法——CMM方法,并以同轴线为例,展示了这种方法的计算过程。首先通过保角变换,建立同轴线与平行板间的数学联系;然后,利用曲线坐标建立了场源在同轴线和平行板间的映射关系,得出了同轴线的场源分布;最后,利用同轴线中的场分布建立了同轴线等效电路模型,模型中与电路传输特性相关的参量与电容紧密相关,且电容与传输线的尺寸相关,这样就形成了一个完整的分析与设计过程。本文方法相比于以电位为中间量的传统保角变换,直接从场出发,省去了关于电位的中间计算过程,在保证计算精度的同时,有效节约了计算资源。仿真结果表明,不同尺寸下同轴线特征阻抗仿真值与理论值吻合得很好,说明了CMM方法的正确性。本文方法并不局限于真空环境,也适用于各向同性介质,且有望推广到三维微波器件。
[1] DEY S, MITTRAA R. Locally conformal finite-difference time-domain (FDTD) algorithm for modeling three-dimensional perfectly conducting objects [J]. IEEE Microwave and Guided Wave Letters, 1997, 9(7): 273-275.
[2] HAMILTON L R, STALZER M A, TURLEY R S. Method of moments scattering computations using high-order basis functions [EB/OL]. [2015-03-05]. http:/ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=385149.
[3] 崔翔, 谢羲. 计算电容值的变分与互补变分法 [J]. 华北电力学院学报, 1990, 17(2): 1-6. CUI Xiang, XIE Xi. Variational and complementary variational method for calculating capacitance [J]. Journal of North China Institute of Electric Power, 1990, 17(2): 1-6.
[4] 倪中非, 黄斌科, 师振盛. 用于非规则波导传输特性分析的高效坐标变换法 [J]. 西安交通大学学报, 2014, 48(8): 18-22. NI Zhongfei, HUANG Binke, SHI Zhensheng. An efficient coordinate transformation method for propagation properties analysis of irregular waveguide [J]. Xi’an Jiaotong University, 2014, 48(8): 18-22.
[5] PENDRY J B, SCHURIG D, SMITH D R. Controlling electromagnetic fields [J]. Science, 2006, 312: 1780-1782.
[6] 梁昌洪, 崔铁军, 范小平. 采用保角变换求解一类TEM模传输线的衰减常数 [J]. 电子科学学刊, 1991, 13(5): 475-481. LIANG Changhong, CUI Tiejun, FAN Xiaoping. Conformal transformation method for attenuation constant of TEM mode transmission line [J]. Journal of Electronics, 1991, 13(5): 475-481.
[7] DUYAR M, AKAN V, YAZGAN E, et al. Analytical attenuation calculation of asymmetrical coplanar waveguide with finite-extent ground planes for coplanar, waveguide mode [J]. Microwave and Optical Technology Letters, 2007, 49(6): 2082-2087.
[8] ZHAO Ji-Xiang. Characteristic parameters for CPWS on a very thin dielectric layer [J]. Microwave and Optical Technology Letters, 2005, 45(3): 240-241.
[9] AKAN V, YAZGAN E. Quasistatic TEM characteristics of multilayer elliptical and cylindrical coplanar waveguides [J]. Microwave and Optical Technology Letters, 2004, 42(4): 317-322.
[10]SHAN Zhiyong, ZHANG Yanhua, ZHOU Xilang, et al. Analytical analysis of a rectangular shielded multilayer coupled coplanar waveguide [J]. Microwave and Optical Technology Letters, 2004, 41(5): 392-395.
[11]AKAN V, YAZGAN E. A simple formulation for quasistatic solutions of elliptical, cylindrical and asymmetrical coplanar strip lines [J]. Microwave and Optical Technology Letters, 2004, 41(1): 18-21.
[12]王福谦. 椭圆柱传输线内的TEM波及其特性阻抗 [J]. 光纤与电缆及其应用技术, 2011(5): 1-3, 11. WANG Fuqian. TEM wave and characteristic impedance of the elliptical cylinder transmission line [J]. Optical Fiber & Electric Cable, 2011(5): 1-3, 11.
[13]李宗谦, 佘京兆, 高葆薪. 微波工程基础 [M]. 北京: 清华大学出版社, 2004: 113-114.
(编辑 刘杨)
A Conformal Mapping Method Based on Curve Coordinates under Complex Electromagnetic Boundaries
ZHANG Jingsi1,MIAO Yingkai2,LIU Xiaobo1,ZHANG Anxue1
(1. School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. Puyang Vocational and Technical College, Puyang, Henan 457000, China)
A conformal mapping method (CMM) based on curve coordinates is proposed to focus on the problem that the electromagnetic field of the two-dimensional uniform microwave transmission lines with complex geometric boundary conditions is hard to be analytically solved and thus its design is difficult. The method is based on a TEM model of the cross-dimensional electromagnetic transmission line. First, the conformal mapping is used to map the complex boundary curve of the transmission line into boundary curves of a simple transmission line, and the curvilinear coordinates of the complex border transmission lines are built; Then the curvilinear coordinates are used to convert the Maxwell’s equations for the complex border transmission lines to the simple border transmission lines, and the electromagnetic mapping between the two kinds of transmission line is formed. Finally, it is verified that both the charge and the potential between two kinds of transmission lines are correspondingly equal, so that the capacitance of complex transmission line that is closely related to the transfer characteristic is obtained and can further be used to guide the design of the transmission line. Simulation results and comparisons with the traditional conformal mapping calculation method with the potential being the intermediate amount show that the CMM method starts directly from the field, eliminates the potential on the intermediate calculations, and its results agree well with theoretical calculation.
microwave transmission lines; curve coordinates; conformal mapping; Maxwell’s equations
2015-04-30。
张婧思(1992—),女,硕士生;张安学(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61471292,61331005,61471388,41404095)
时间:2015-11-27
10.7652/xjtuxb201602008
TN81
A
0253-987X(2016)02-0043-05
网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151127.2116.006.html

