“直线与圆的位置关系”教学实录与思考

金 洁●

浙江省杭州第二中学(310000)



“直线与圆的位置关系”教学实录与思考

金 洁●

浙江省杭州第二中学(310000)

教材是实施教学，实现课程目标的重要资源.为了更好地发挥教材的作用，需要有计划、有目标、有侧重，灵活有效地组织教学，拓展教学空间，这就需要对教材进行二次开发，变“教教材”为用“教材教”，从而更好地促进学生主动探究学习.笔者以“直线与圆的位置关系”课堂实录为例，反思教学中如何重视教材、挖掘教材、创造性地开发教材.

直线与圆的位置关系；教学；实录；反思

一、实际问题引入，激发学习兴趣，培养数学能力

一艘轮船在沿直线返回港口的途中，接到气象台的台风预报：台风中心位于轮船正西60km处，受影响的范围是半径长为40km的圆形区域.已知港口A位于台风中心正北45km处，如果这艘轮船不改变航线，那么它是否会受到台风的影响？(由课本引例改编)

师：若不建立直角坐标系，你能解决该问题吗？

生：利用相似三角形性质，得到相似比，进而求出台风中心到航线的距离，与台风半径进行比较，判断是否受影响.

师：引导学生建立适当的直角坐标系，取10km为单位长度，写出圆方程及航线所在直线方程，问题转化为直线与圆的位置关系.

生：方法一，圆心到直线距离与半径关系来判断；

方法二，联立方程组，通过方程根的情况来判断直线与圆交点个数.

师：通过建立直角坐标系，我们将几何问题代数化，通过代数计算来解释几何问题.

反思：笔者起初也考虑过利用作家巴金《海上日出》的视频片段作为课堂的引入，可以营造良好的教学气氛，体会数学的人文内涵.新课标的理念之一是强调“数学是有用的”，选择教材中的“台风”问题作为引入，恰好体现了这一理念，同时也能很好地体现数学在现实生活、生产中的重要价值，

其次，该问题，课本在旁批处追问“若不建立直角坐标系，你能解决该问题吗？”意在让学生体会几何问题代数化的过程.在学习了直线及圆方程的基础上，解决“台风”问题可通过建立合理的坐标系，利用坐标方法求解，这正是解析几何的核心思想方法.解析几何的初始学习阶段，强化和渗透笛卡尔的坐标法应该是必要的.意在让学生将坐标方法与欧氏几何方法做对比.

还可以将该引例做变式提问“若不改变航线，受台风影响的时间有多久？”“为避开台风，如何设计航线？”考虑到课堂的教学时间有限，可以将某些比较开放的问题延伸至课外探究.

二、学生主体探究，教师引导总结，形成新知识

师：通过刚才解决问题的过程，我们可以总结如何判断直线和圆的位置关系.

生1：利用点到直线距离公式求得弦心距，通过比较弦心距和半径的关系确定直线和圆的位置关系.

生2：联立方程组，通过对方程根的情况的判断，确定直线和圆的交点个数.

教师总结，并用图表的形式强调知识点.

师：直线和圆的三种几何关系，我们都可以通过不同程度的代数计算来刻画.

三、依据典型例题，搭建探究实践的问题阶梯

例1 (课本例题改编)已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0，判断直线l与圆的位置关系；如果相交，求它们的交点坐标及弦长.

师(追问)：你能求出弦|AB|的长吗？

师(追问)：在不求出交点坐标的情况下，能否求出弦|AB|的长呢？

师：当直线和圆相交时，我们在研究交点、弦长的过程中，使用了两种方法，能否请同学们谈谈这两种方法在解决问题时的特点吗？

生1：方法一简单，计算量也小，解决问题时应充分利用圆的几何性质.

生2：求交点坐标的方法可以不依赖图形.

师：充分利用圆的几何性质，抓住圆心与弦中点构成的直角三角形，可以简化计算过程，通过计算点到直线距离，并与半径大小作比较，将几何问题进行了代数刻画、定量分析.另一位同学将直线与圆联立方程，通过消元，方程的根即图形交点的横坐标，通过方程的意义来刻画几何问题中的交点情况.

设计意图：该例题选取课本例1，通过对例1的解决和探究，使学生进一步掌握判断位置关系的方法，获得弦长公式.在求交点坐标时需要联立方程求解，求弦长则可以利用垂径定理构造直角三角形求解，也可利用方程韦达定理求解.令学生体会坐标法的过程，学会用代数计算来解决几何问题.

例2 (课本例题改编)已知点M(-3,-3)和圆C:x2+y2+4y-21=0.

(1)若过点M的直线被圆C所截得的弦长为8，求直线l的方程.

(2)当弦被M平分时，求直线l的方程.

师：请同学点评.

生2：第一问设直线方程时没有考虑斜率不存在的情况，实际上，当x=3时也符合题意.

师：我们要注意思维的严谨，直线点斜式方程有其局限性，解决问题时不要遗漏斜率不存在的情况.

师(追问)：过M作直线与圆相交，弦长为8的弦有几条？所得弦长AB的取值范围是多少呢？何时最短？何时最长？

师：过点M最长弦及最短弦具有唯一性，除此之外，过点M弦长为定值的弦均有两条.

设计意图：例2仍选自课本，但做了改编，令符合条件的其中一条直线斜率不存在，此处设计的目的，是为了警示学生在设直线点斜式方程时常常出现遗漏的错误，同时从几何角度解释，过圆内一定点的弦，其中以定点为中点的弦最短，过定点及圆心的弦(即直径)最长，除此之外等长的弦有两条.进一步令学生体会几何直观给我们的研究明确了方向，代数定量计算常常同几何定性分析互为补充，培养数形结合的思想方法，形成严谨治学的学习态度.

师：同学们考虑若点M为圆上一点，如何求圆的切线方程？若点M为圆外一点，又如何求圆的切线方程？

例2 (变式) 已知圆C:x2+y2+4y-21=0.(1)求过点M(4,1)的圆的切线方程；(2)求过点N(5,4)的圆的切线方程.

生2：由平面几何知识可知，过圆外一点应有两条圆的切线，点N(5,4)在圆外，怎么会只有一条切线呢？

生3：在代数求解的过程中，设切线的点斜式方程有局限性，遗漏了直线斜率不存在的情况，所以过点N(5,4)的切线应为11x-60y+185=0和x=5.

师：代数计算和几何直观互为补充能令问题更为清晰明朗.在运用直线方程时要谨记各方程的局限性，避免漏解.

师：另外，可否得到一般结论？请同学们探讨过圆C:(x-a)2+(y-b)2=r2上一点P(x0,y0)的切线方程.

生1：已知圆心坐标为C(a,b)，切点P(x0,y0)，设切线上任一点Q(x,y)，由平面几何性质可知，PQ⊥PC，①当x0=a时，y=y0.

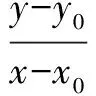
综上所述过圆C:(x-a)2+(y-b)2=r2上一点P(x0,y0)处的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.

师：第一位同学利用切线的几何性质，用坐标表达垂直关系，得到切线方程.第二位同学结合向量数量积的几何意义，通过向量的坐标运算得到动点轨迹.我们体会到了从几何到代数的过程，将几何问题代数化，用代数语言描述几何要素及其关系，进而将几何问题转化为代数问题.

接下来请同学们思考：若点P(x0,y0)为圆外一点，过点P的圆的切线有两条，则方程(x0-a)(x-a)+(y0-b)(y-b)=r2的几何意义是什么？

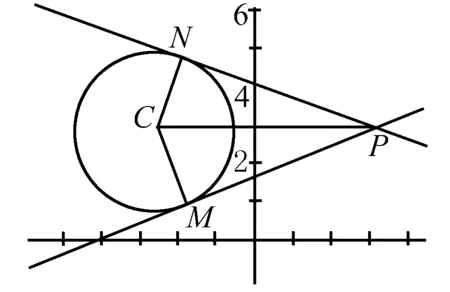
师：该问题令我们思考代数方程背后的几何意义.解析法，即通过数形结合，完成代数和几何之间的相互转化.

设计意图：对课本例2的变式设计，令问题层层递进深入.进一步探究圆的切线问题，在此过程中培养学生数形结合思想，体会一个几何对象用代数方式完全刻画，几何概念可以表示为代数的形式，几何目标可以通过代数方法来达到；反之，代数语言得到了几何解释，从而代数语言有了直观意义，从中得到启发而提出新的结论.

四、教学反思

本课的教学目标是使学生能够根据直线与圆的方程，判断直线与圆的位置关系，充分体会解析几何的核心思想——坐标法，培养数形结合思想，令学生感悟几何和代数的密不可分.“只要代数与几何分道扬镳，它们的进展就缓慢，它们的应用就狭窄.但是当这两门科学结成伴侣时，它们就互相吸取新鲜的活力，就以快速的步伐走向完善.”

教学设计充分利用教材资源，深层挖掘，由浅入深地推进课堂.著名的数学教育家波利亚曾形象地指出：“好问题同某种蘑菇有些相像，它们都成堆地生长，找到一个以后，你应当在周围找一找，很可能附近就有好几个.”由教材的基本问题出发，设计问题串，引导学生更多地参与投入到探究中，有效地理解和掌握学科知识，激发学习的好奇心及挑战欲.让学生在探究解决问题的过程中获取新知识，潜移默化地形成思想方法，培养数学化的思维方式.

在教学过程中，尊重学生的主体作用，体现教师的引导功能，激发学生自主探究，教师适时总结提升.给学生充足的思维空间，通过对话和交流引导学生独立探索、发现规律和建构知识，力求让学生达成探究性理解.总之，守本和创新是相辅相成的，教师扎根于教材的同时，发挥创造力的课堂设计才是我们追求的方向.

G632

B

1008-0333(2016)24-0004-02