“两个变量的线性相关”的教学设计与分析

李 娜●

山东烟台鲁东大学数学与统计科学学院(264000)



“两个变量的线性相关”的教学设计与分析

李 娜●

山东烟台鲁东大学数学与统计科学学院(264000)

在两个变量线性相关这堂课的教学设计中，围绕“怎样求得线性回归方程”这一问题，在教师的引导下使学生进行有目的的探究，推导求出线性回归方程，并能够在解决实际问题中得到应用.

教学设计、最小二乘思想、线性回归方程

新课标下的数学课堂，教师应采用以学生为主体，教师为主导的教学方式，不仅使学生学会知识，更重要的是理解知识，明白知识的产生和推导过程.线性相关这一概念对于学生来说比较抽象，且内容枯燥，尤其是回归直线方程的推导过程麻烦，逻辑性强，一般学生依靠自己不能够找出正确的求解方法，在这种情况下，要更好地引导学生积极地探究，让学生在探究的同时，学好知识，体会数学方法的神奇之处.

一、教材与学情分析

1.教材课题

人民教育出版社B版必修三第二章2.3.2《两个变量的线性相关》，共1课时.

2.学情分析

学生已经具备了对样本数据进行初步分析的能力，能根据两个相关变量的数据作出散点图，学生思维活跃，已初步形成对数学问题的合作探究能力.但在高中阶段，学生首次接触“最小二乘法”，容易产生认知上的困难.

3.教学目标

(3)知识与技能目标：能根据散点图直观判断变量间的线性相关关系；了解最小二乘法的思想；能根据给出的回归系数公式建立线性回归方程.

(3)过程与方法目标：经历用不同估算方法描述两个变量线性相关的过程，发展统计观念；感受最小二乘法求解回归系数的探究过程.

(3)情感态度与价值观目标：通过对最小二乘法求回归方程系数的探究过程，培养学生勤于思考、勇于探索的科学精神.

4.教学重难点

(1)教学重点：回归直线方程的概念及根据回归系数公式建立回归直线方程.

(2)教学难点：线性回归及最小二乘法求回归直线方程的思想的建立.

5.教学方法

探究式和启发式教学方法.

二、教学过程

环节1：复习旧知——方法巩固

教师在屏幕上展示以上图片，并让学生观察分析每幅图中的散点间是否存在关系.

设计意图：散点图是观察两个变量关系的直观手段，在此复习,既可以使学生复习旧知，也为本节课研究两个变量线性相关做铺垫.

环节2：创设情境——引入新课

教师在屏幕上展示这样一道情景题：下表是某小卖部6天卖出热茶的杯数与当天气温的对比表：

气温/℃261813104-1杯数202434385064

(1)将表中的数据画成散点图.(2)你能从散点图中发现温度与饮料杯数近似成什么关系吗？(3)猜测当气温为-3℃时，卖出热茶的杯数为多少？

教师先让学生自己动手画出散点图，散点图完成后，再提醒学生观察图并思考问题(2)，同时教师在屏幕上展示一组判断题：a.卖出热茶的杯数与温度没有什么关系；b.图中散点在一条直线上；c.就整体而言，散点大致分布在一条直线附近.

设计意图：通过实际情境并结合问题，引导学生思考；通过一组判断题，为接下来引入回归直线的概念做好铺垫.

环节3：探索研究——学习新知

结合以上分析，教师给出这样两个概念：

回归直线：如果散点图中点的分布从整体上看大致在一条直线附近，就称这两个变量之间具有线性相关关系，这条直线称为回归直线.

设计意图：结合引例对回归直线及回归直线方程两个概念进行讲授，便于学生对知识的理解.

教师提出这样两个问题：如何作出回归直线？回归直线应该满足哪些条件？让学生分组讨论，给出各小组意见，教师对各小组意见进行归纳总结，整理为以下三点：(1)经过散点最多的直线(2)使分布在直线两侧的散点个数相同的直线(3)使所有点到直线的距离和最小

设计意图：求回归直线方程的思路灵活，所以让学生进行小组合作，使每个学生都能参与其中，同时教师加以总结，防止思路混乱，在肯定学生探索精神的同时，正确引导学生.

接下来教师带领学生分别验证提出的三种可能性.通过分析，很明显(1)(2)两种情况不满足回归直线的条件，这里不做赘述.

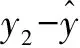
通过以上分析(计算过程繁琐，不在赘述)，从而归结出使得Q最小的最简方式，即最小二乘法.

设计意图：通过一系列的探究活动，使得学生不仅知道公式，还能理解公式是怎样推导出来的，让学生能够更好的掌握和理解回归直线.

环节4:知识运用——概念巩固

教师将问题再次回到情境问题中的第三问.

设计意图：通过对问题的解决，使学生真正的认识到线性回归方法的可用性，同时使得整堂课首尾呼应.

环节5:课堂小结——布置作业

教师以提问的方式，带领学生回顾新课内容，并布置作业.

三、总结

本节课的教学难点是回归直线方程的建立，针对此难点我设计了推导回归直线方程的三个思路，逐步引导学生探索，使学生在探索中得出结论，这样的设计比教师直接给出计算公式能更好的使学生理解，课上效果也非常理想，学生能够更好的参与课堂并获取知识.

G632

B

1008-0333(2016)24-0013-02