一道抛物线定点问题的奇妙变题及推广

江苏省兴化市第一中学 (225700)

葛新燕



一道抛物线定点问题的奇妙变题及推广

江苏省兴化市第一中学 (225700)

葛新燕

一、奇妙的变题

问题 过抛物线y2=2px的顶点O作互相垂直的直线OA,OB与抛物线相交于另两点A,B，求证：直线AB经过定点(2p,0)．

本题是一道常见的抛物线习题，以此题作为题根而编制的试题比比皆是．一种有趣的思考是：作点B关于x轴的对称点B′，那么直线AB′是否仍然经过定点呢？通过几何画板进行实验，验证了这一猜想的正确性，并发现定点为(-2p,0)．这一有趣的事实激发了笔者的探索欲望．

由于原题中OA,OB互相垂直，所以它们的斜率积为-1．相对于原题，此时直线OA,OB′有何特征呢？考察OA,OB′的斜率，发现关系并不明显．转换思维角度，从倾斜角的角度考察发现，直线OA,OB′的倾斜角之和为90°，从而斜率积为1．下面，从倾斜角和为90°这一角度叙述该变题．

定理1 过抛物线y2=2px的顶点O作直线OA,OB与抛物线相交于另两点A,B，若直线OA,OB的倾斜角之和为90°，则直线AB过定点(-2p,0)．

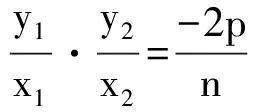
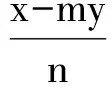
二、问题的纵向推广

定理1的条件具有极大的自由度，发展空间很大；另一方面，有力的方法不仅使原问题获得了简解，也为我们进一步研究问题打开了思路．

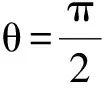
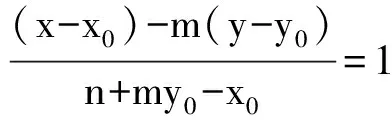
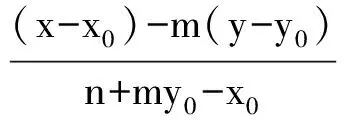
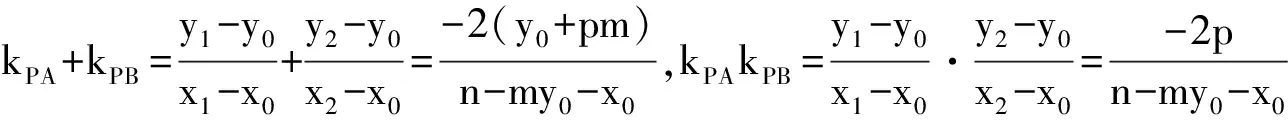
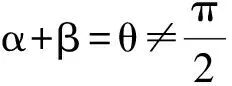
三、问题的横向推广

抛物线是圆锥曲线的一种，它和椭圆、双曲线有着割舍不断的血缘关系，因此，我们自然会思考：椭圆和双曲线中是否也存在类似的定点呢？

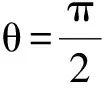
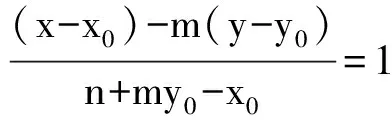
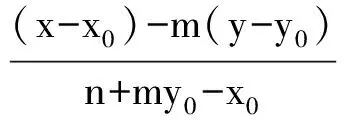
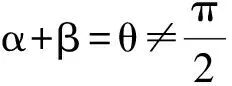
说明：当u>0,v>0,u≠v时，ux2+vy2=1表示椭圆；当uv<0时，ux2+vy2=1表示双曲线．

四、问题的统一推广

从成功的喜悦中抽出身来，回到起点，将原题和变题进行比较发现OA,OB的斜率之积分别为-1,1，都是定值，从这个角度，我们可将它们统一推广为(证明略)：

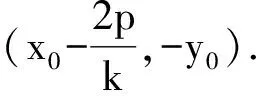
类似的，我们有：

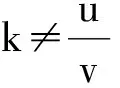
我们从一道常见的抛物线定点问题出发，由浅入深，由此及彼，动中寻静，探索发现了圆锥曲线中一组耐人寻味的定点．无序的运动中蕴藏着静态的结果，这是数学的精彩和魅力，数学之美妙着实令人如痴如醉．