换元让问题进入方程(组)，消元使问题在一个方程中

重庆市荣昌大成中学 (402460)

熊福州



换元让问题进入方程(组)，消元使问题在一个方程中

重庆市荣昌大成中学 (402460)

熊福州

文[1] 文[2]根据著名数学大师笛卡儿的方程理论(一切问题都可数学化,化归为数学问题,一切数学问题都可化归为代数问题,一切代数问题都可化归为方程问题,有了方程理论就可解决一切问题)研究后指出：数学问题的根基本质是方程的解集，最基本的数学思想方法是方程思想，换元(消元)法，即换元(设未知数,即用字母代数或式)产生方程(组),问题就自然进入方程、不等式(组),消元使问题在一个方程(不等式)中，求方程(不等式)的解集(在坐标系上就是图像)就自然解决问题(可解的话),因此，换元，消元是最基本的解题思路和方法.一切代数问题一般都应考虑列、解方程(或由方程产生的不等式(组))解决.下面以文[3]的某些例和高考题说明.

例1 求方程2x2-2xy+5y2-10x-4y+17=0的所有实数解.

解:令2a+b+c=k,得方程组

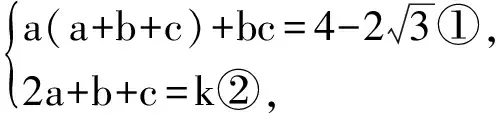
例3是2006年全国高考重庆卷理10,有相当的难度,参考解答对代数式变形能力要求较高,有技巧,却不易想到,换元为方程就好想了,解法也多了.

注:作差比较法证明不等式实质是求差函数(代数式)的值域(解集),换元为方程后就是方程(组)中求取值范围(解集).一般地,未知数的个数与方程个数相同,求取值(有限解集), 未知数的个数多于方程个数,求取值范围(无限解集).表示实数的字母(未知数，即元)进入方程(组), 取值范围(解集)就确定了(现在比较流行的说法叫“隐含条件”),消元后最终得到多个未知数的一个方程,再解出一个未知数得显函数(在高中，多为求一元显函数),求显函数的定义域和值域就自然得到了，因此，“换元让问题进入方程(组)，消元使问题在一个方程中”是最基本的解题思路.

[1]熊福州,张龙跃.数学问题的根基本质是方程的解集[J].中学数学研究(江西),2015,8.

[2]熊福州.最基本的数学思想方法——方程思想，换元法[J].河北理科教学研究,2000,4.

[3]罗增儒.数学解题引论[M].陕西师大出版社，1997,6.