利用定积分证明不等式三例

安徽省怀宁中学 (246121)

鲍翊虎



利用定积分证明不等式三例

安徽省怀宁中学 (246121)

鲍翊虎

新课程改革中，高中数学以选修方式教学了定积分，本文选用三道不等式证明类型的试题，借助定积分加以解决，旨在提升学生应用知识的能力，从而深化对定积分的理解！

一、利用定积分实现不等式的数形结合

(1)用a表示出b，c；

(2)若f(x)≥lnx在[1,+∞)上恒成立，求a的取值范围；

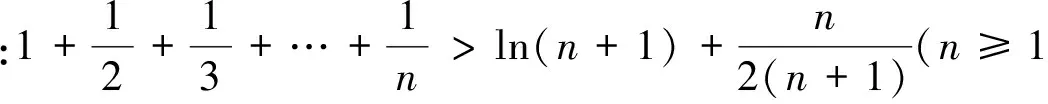
图1

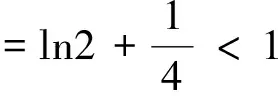
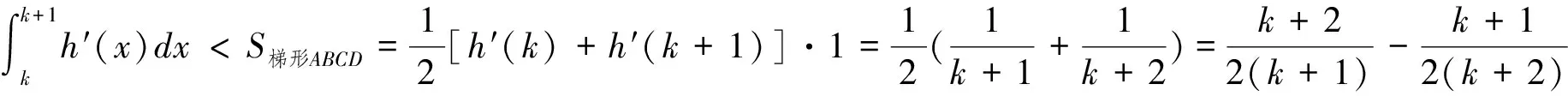
根据①和②可知，不等式对任何的n∈N*都成立.

点评：在本题的教学中，利用构造函数证明(3)时，技巧性太强，虽然体现了试题的上下联系，但是给学生的感受只是惊叹；由式子结构特点而联想到定积分，这激发了全班同学的探究热情，可见知识的交汇对学生创造性思维的培养是多么受欢迎！

二、为累和型不等式的证明提供一种新方法

例2 (2012天津理20)已知函数f(x)=x-ln(x+a)的最小值为0，其中a>0.

(1)求a的值；

(2)若对任意的x∈[0,+∞),有f(x)≤kx2成立，求实数k的最小值；

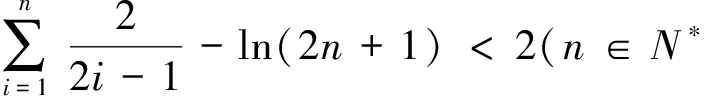
图2

(1)设函数F(x)=f(x)-h(x)，求F(x)的单调区间与极值；

图3

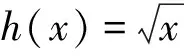
点评：例2和例3主要考查学生综合运用所学知识进行推理论证、运算求解的能力，参考答案的解答过程流畅且优美；但是，试题中代数式的和式结构若被面积化，则定积分拥有了彰显的舞台，通过计算替代逻辑推理，降低了试题的难度！