函数中含参数零点问题的求解策略

宁夏彭阳县第三中学 (756500)

杏望春



函数中含参数零点问题的求解策略

宁夏彭阳县第三中学 (756500)

杏望春

函数零点是函数单元中的重要内容，它常常与方程、不等式等知识交汇，涉及到的题型大多是求参数取值范围问题，给同学们的学习带来一定的困难.为此，我们结合具体实例给出与零点相关问题的以下几种常见的求解策略，以期对同学们的学习有所帮助.

1.把函数零点问题转化为方程根的问题

利用函数y=f(x)的零点⟺方程f(x)=0的根.把求函数零点的相关问题转化为求方程根的问题，通过方程的根所满足的条件建立不等式来解决问题.

例1 若二次函数f(x)=x2-2ax+4在区间(1,+∞)内有两个零点，求实数a的取值范围.

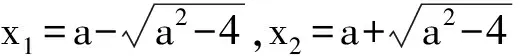
评析：若函数对应的方程的根易求得，我们可以通过解方程求出根，然后根据方程根所满足的条件建立不等式组，从而求出参数的取值范围，是解决这类问题的常用方法.

2.把函数零点问题转化为函数图像与坐标轴的交点问题

利用函数y=f(x)的零点⟺函数y=f(x)的图像与x轴交点.把函数零点的相关问题转化为图像与坐标轴的交点问题，再利用数形结合的思想方法来解决问题.

解：f′(x)=x2+(1-a)x-a=(x-a)(x+1),由f′(x)=0得x=a，x=-1.列表

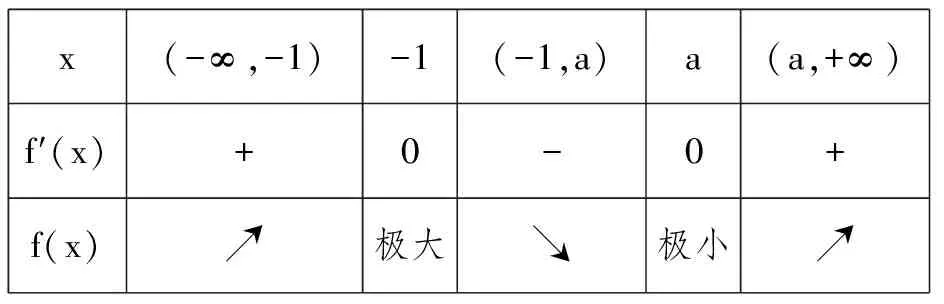
x(-∞，-1)-1(-1，a)a(a，+∞)f′(x)+0-0+f(x)↗极大↘极小↗

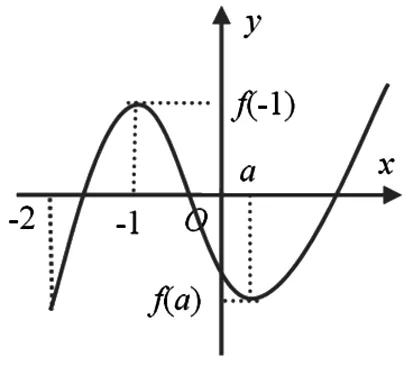
图1

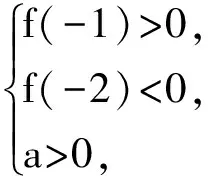
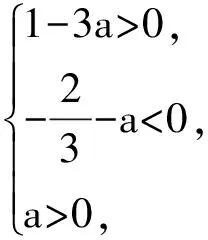
评析：利用函数的简单性质做出函数的图像，借助于图像分析零点在所给定区间上时，图像所满足的条件建立不等式组求解.通过数形结合的方法轻松解决.

3.把零点问题分离变量后转化为函数值域问题

将函数零点问题先转化为方程根的问题,然后进行变量分离，将参数分离出来转化为求函数值域问题.这种方法思路简洁，学生容易想到.

例3 已知a为实数，函数f(x)=2ax2+2x-3-a，如果函数y=f(x)在区间[-1,1]上有零点，求a的取值范围.

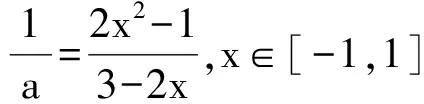
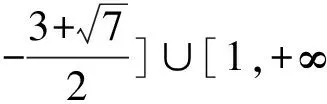
4.把函数零点问题转化为两个函数图像的交点问题

将函数零点的个数问题通过等价转化为两个函数图像的交点个数问题，再借助图像找出所满足的

条件，建立不等式或不等式组是解决与函数零点相关问题的重要策略.

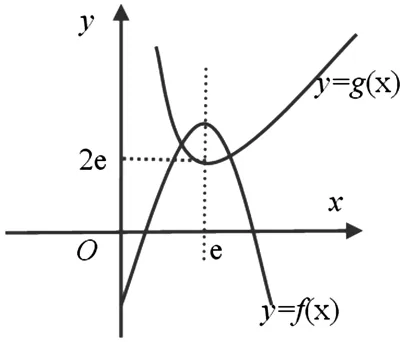
图2

解：要使h(x)=g(x)-f(x)有两个零点，只需函数y=g(x)与函数y=f(x)的图像有两个交点.由函数的性质作出函数y=g(x)的图像如图2所示.

因为f(x)=-x2+2ex+t-1=-(x-e)2+t+e2+1，所以函数y=f(x)的图像的对称轴为x=e，最大值为t+e2+1.只有当t+e2+1≥2e，即t≥-e2+2e-1时，函数y=g(x)与函数y=f(x)的图像有两个交点.故t的取值范围为[-e2+2e-1,+∞).