一个二次曲线定理的再推广
2016-12-16 08:20朱晶
数理化解题研究 2016年28期
朱 晶●
江苏省镇江中学(212017)
一个二次曲线定理的再推广
朱 晶●
江苏省镇江中学(212017)
在综合二次曲线的两个关于直线恒过定点的结论之后,将其进一步推广,得到更一般的结论.
二次曲线;定点;定值;斜率
文[1]给出了二次曲线的一个定理如下:
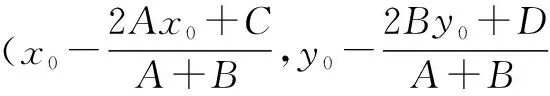
文[2]通过对圆的一个常见结论进行推广,得到如下

受文[1]、文[2]的启发,笔者想到:文[1]中的“PM⊥PN”,就是文[2]中的“C=-1”,如果将文[1]中的“PM⊥PN”改为“kPM·kPN=t(t为常数)”,直线MN是否恒过定点?通过研究,得到一个肯定的结果.


把②代入①,则二次曲线Γ在新系x′Py′中的方程为:A(x′+x0)2+B(y′+y0)2+C(x′+x0)+D(y′+y0)+E=0,
整理得Ax′2+By′2+(2Ax0+C)x′+(2By0+D)y′=0 ③.
设MN在新系x′Py′中的方程为mx′+ny′=1,代入③得Ax′2+By′2+[(2Ax0+C)x′+(2By0+D)y′](mx′+ny′)=0.
整理得: [A+(2Ax0+C)m]x′2+[B+(2By0+D)n]y′2+[(2Ax0+C)n+(2By0+D)m]x′y′=0.

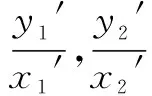
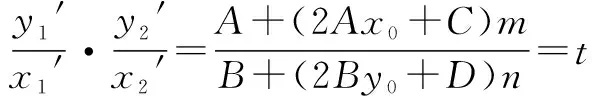
(1)当A=tB时,则由⑤得(2Ax0+C)m=(2By0+D)nt.


2.定理的三个推论
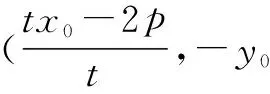

[1]沈新权.二次曲线内接直角三角形斜边过定点的一个统一结论及推广[J].数学通讯,2010(1).
[2]徐道.一个平面几何结论的解析推广[J]. 中学生数学(高中版),2010(11).
G632
B
1008-0333(2016)28-0033-01
猜你喜欢
陇东学院学报(2022年5期)2022-08-31
中学生数理化(高中版.高考数学)(2022年4期)2022-05-25
今日农业(2021年21期)2021-11-26
新世纪智能(教师)(2021年2期)2021-11-05
教育周报·教育论坛(2021年21期)2021-04-14
中学生数理化(高中版.高二数学)(2020年12期)2021-01-13
华人时刊(2020年17期)2020-12-14
华人时刊(2020年17期)2020-12-14
云南教育·中学教师(2019年12期)2019-08-13
数学学习与研究(2016年19期)2016-11-22

