机动目标当前统计模型模糊自适应算法
刘望生, 潘海鹏, 李亚安
(1.浙江理工大学 机械与自动控制学院, 浙江 杭州 310018; 2.西北工业大学 航海学院, 陕西 西安 710072)
机动目标当前统计模型模糊自适应算法
刘望生1, 潘海鹏1, 李亚安2
(1.浙江理工大学 机械与自动控制学院, 浙江 杭州 310018; 2.西北工业大学 航海学院, 陕西 西安 710072)
针对当前统计模型常规算法跟踪机动目标的缺陷,提出了当前统计模型模糊自适应算法。该算法根据规范化的量测新息及其变化率并通过模糊推理实时选取机动频率,给出了加速度方差的新息幂函数调整方法,采用加速度估计值和预测值的偏差在线更新当前加速度均值。在此基础上,结合高斯隶属函数和强跟踪算法对其权值予以修正。当前统计模型模糊自适应算法不受机动频率人为给定和最大加速度极值设置的限制,适用于不同范围和程度的机动。利用当前统计模型模糊自适应算法对阶跃机动、圆周机动、Jerk机动3种典型机动场景进行了计算机仿真,并与当前统计模型常规跟踪算法和Jerk模型自适应算法进行了比较。仿真结果表明,该算法扩大了跟踪范围,具有较好的稳态特性和瞬态特性,其跟踪精度和收敛速度优于其他两种算法。
兵器科学与技术; 当前统计模型; Jerk模型; 模糊自适应; 强跟踪; 机动目标
0 引言
机动目标跟踪是指系统模型存在突变的状态估计问题,目标机动会导致目标的动力学特性发生变化,为了从观测中最优地提取有关目标运动状态的有用信息,学者们提出了大量解决机动目标跟踪问题的方法[1-6]。这些方法大致可分为两类[7]:需要机动检测与补偿过程的单模型法和基于马尔科夫跳变的多模型法。多模型法跟踪性能受模型复杂度和模型转移概率的影响,机动检测的单模型法存在暂态误差和时间滞后问题。过程噪声自适应的单模型法主要是将目标机动看作是状态噪声方差的加入,比较典型的有Singer模型、半马尔可夫模型、Jerk模型、当前Jerk模型以及当前统计模型[8-12]。Singer模型采用零均值特性描述目标机动不合理,半马尔可夫模型需预先确定大量机动加速度均值,Jerk模型在跟踪Jerk机动时存在确定性稳态误差,当前Jerk模型在跟踪阶跃机动时收敛速度慢,容易发散。对目标机动适应能力较强的模型是当前统计模型。
当前统计模型采用非零均值和修正瑞利分布来表征机动加速度的统计特性,更符合目标实际机动,但当前统计模型常规算法对机动目标的跟踪存在以下缺陷:1)采用固定机动频率不符合机动实际;2)机动加速度极值很难预先确定,且不能自适应调整;3)当前加速度预测值作为修正瑞利分布的均值导致变加速机动时估计误差偏大。许多文献给出了机动频率α的在线调整和不同α的多模型交互,以使模型更接近目标真实机动[13-14]。文献[15]提出了加速度方差状态分量综合自适应法,机动频率的选取采用交互多模型算法自适应完成,提高了跟踪精度,但将加速度一步预测值作为当前加速度均值限制了跟踪变加速机动时的性能;文献[16]引入Jerk输入估计改进了当前统计模型的状态方程和机动加速度方差调整方法,利用改进的无迹强跟踪滤波器实现了状态协方差、状态噪声协方差和机动频率的联合自适应,但其跟踪机动目标的范围仍有限。
本文在分析当前统计模型跟踪机理的基础上,根据规范化的量测新息及其变化率,并通过模糊推理实时选取机动频率,给出了加速度方差的新息幂函数调整方法,采用加速度估计值和预测值的偏差更新当前加速度均值。在此基础上,结合高斯隶属函数和强跟踪算法对其权值予以修正,提高了当前模型跟踪弱机动时的精度,改善了跟踪突变机动的性能。仿真结果验证了本文所提算法的有效性。
1 当前统计模型常规算法
当前统计模型离散状态方程[12]为
(1)
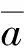
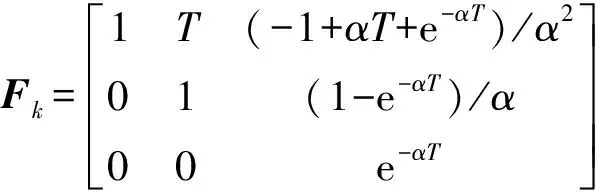
(2)

(3)

(4)
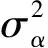
Yk=HkXk+vk,
(5)
式中:Yk为装态向量;Hk为量测矩阵;vk是零均值高斯白噪声,其方差为Rk. 则滤波过程为
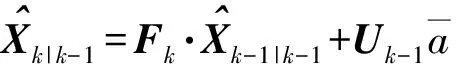
(6)
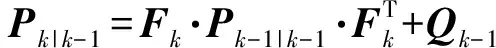
(7)

(8)

(9)
Pk|k=[I-Kk·Hk]·Pk|k-1.
(10)
机动加速度方差为
(11)
式中:amax为给定的最大加速度。该算法将当前加速度均值引入预测方程,使当前统计模型变为方差自适应的匀加速模型[17]。采用固定机动频率α跟踪机动目标存在模型失配,仅靠调节机动加速度方差很难兼顾非机动、弱机动和阶跃机动的性能,且对变加速机动跟踪效果变差。因此有必要对α实行在线调整。
2 模糊自适应算法
2.1 机动频率模糊选取
由于量测新息和量测新息的变化率能够较好地反映目标的机动强度[18],可通过量测新息及其变化率对α进行实时调节。为便于模糊推理,采用规范化的量测新息及其变化率作为模糊输入变量。假定量测向量是二维,输入变量定义[19]为
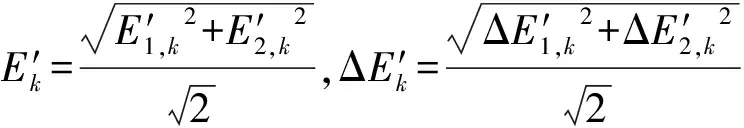
(12)
式中:E′1,k、E′2,k、ΔE′1,k、ΔE′2,k为量测向量各分量的规范化新息和新息变化率,取值范围为[-1,1];E′k、ΔE′k为综合的规范化新息和新息变化率,取值范围为[0,1]。
在文献[18]和文献[19]的基础上,本文的E′1,k和ΔE′1,k计算方法分别为
(13)
(14)

假定输入变量E′k和ΔE′k的模糊集为LP(正大)、MP(正中)、SP(正小)、ZE(零),隶属度函数采用梯形函数。输出变量为[0,1]间的比例系数μ,其模糊集为EP(正极大)、VP(正非常大)、LP(正大)、MP(正中)、SP(正小)、ZE(零),隶属度函数采用三角形函数。定义输入输出变量并进行模糊化后,可利用表1的模糊规则进行模糊推理,模糊规则由专家经验获得[20]。模糊推理机采用Mamdani方法,系统的模糊输出是通过对有效的模糊输出做最大化运算。
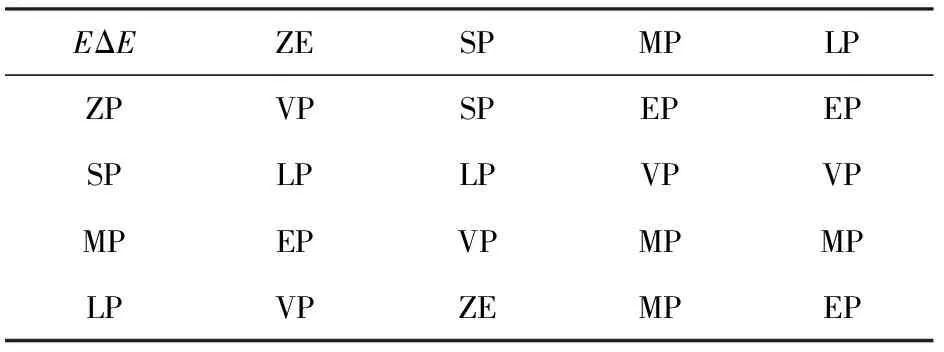
表1 模糊关系表
对给定的E′k和ΔE′k值,可以得到反映目标机动强度大小的比例系数μ,根据μ值实时调节目标的机动频率,使当前统计模型参数在弱机动和强机动之间进行切换。机动频率的调整公式为
α=αmin(1-μ)+αmaxμ,
(15)
式中:αmin为非机动和弱机动时的机动频率;αmax为强机动时的机动频率;μ为模糊推理得出的值。
2.2 机动加速度方差调整
为克服当前统计模型常规算法对加速度极值的依赖,在文献[21]的基础上,根据调整后的当前统计模型预测目标机动加速度均值,其方差采用新息幂函数表示为
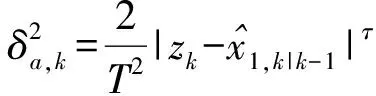
(16)
式中:τ为幂指数,在给定的噪声背景下可根据经验设定。当目标发生较大机动时,测量值与状态位置分量预测值的差值增大,采用新息幂函数能使系统以较大的方差跟踪,收敛速度快。受观测噪声的影响,新息幂函数调整法仍不能较好地跟踪弱机动,为此引入高斯隶属函数对方差进行修正,即

(17)

2.3 输入加速度更新
将目标机动看作状态噪声方差的加入存在暂态误差和时间滞后,由于目标机动的不确定性,采用加速度估计值和预测值的偏差来表示输入加速度,可以提高目标机动跟踪时的收敛速度。为了克服非机动时引入加速度的干扰,引入高斯隶属函数对输入加速度进行修正,其表达式为
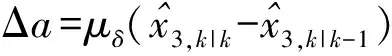
(18)
2.4 强跟踪算法
尽管采用机动频率、加速度方差和输入加速度实时调节能较好地跟踪机动目标,但当目标作阶跃机动时,其动态时延仍较大。引入强跟踪滤波算法,一方面可增强阶跃机动时的跟踪性能,另一方面可平滑弱机动时的滤波精度。设滤波残差为

(19)
则次优渐消因子近似算法[22-23]为

(20)
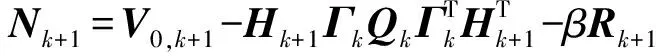
(21)
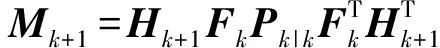
(22)
(23)
式中:Гk为噪声输入矩阵,本文取单位矩阵;0≤ρ≤1为遗忘因子,一般取ρ= 0.95;β为衰减因子,根据经验或仿真设定。此时预报协方差阵计算公式为
(24)
强跟踪滤波算法通过调整滤波增益使残差近似正交,提高了模型的鲁棒性,改善了系统跟踪目标状态突变时的性能。当目标作一般机动,输出残差方差较小,渐消因子λk+1接近1,系统保持了对目标弱机动时的跟踪精度。通过调节β可在强机动和弱机动之间做一折衷。
3 仿真实验及分析
3.1 仿真实验
为了验证当前模型模糊自适应滤波(CSMFAF)算法的有效性,本文对3种典型机动(阶跃机动、圆周机动和Jerk机动)进行了计算机仿真分析,并与当前统计模型卡尔曼滤波(CSMKF)算法和Jerk模型自适应滤波(JMAF)算法进行了比较。其中,JMAF算法采用文献[24]所述方法。仿真是在直角坐标系二维平面内进行,X和Y轴上的量测噪声是均值为0、标准偏差为100 m的高斯序列,扫描周期T=1 s,在CSMKF算法中,最大机动加速度设为amax=100 m/s2、机动频率取0.05,JMAF算法中机动频率设为0.9. 仿真次数为200次。仿真实验中的硬件平台为Intel(R) Core(TM) i7-2600 3.40 GHz处理器,8 G内存,1 T硬盘,软件平台为Windows 7操作系统,Matlab R2010a. 评价的指标分别为位置、速度和加速度的均方根误差,并对3种算法的复杂度、运行时间和平均标准位置差进行了分析。
模拟轨迹1:目标起始时作匀速运动,初速度为300 m/s,在第50~100个扫描区间作匀加速运动,加速度为50 m/s2,在第100~150个扫描区间作匀速运动,在第150~200个扫描区间再作匀加速运动,加速度为150 m/s2,在第200~250个扫描区间恢复匀速运动。仿真结果为图1~图3.
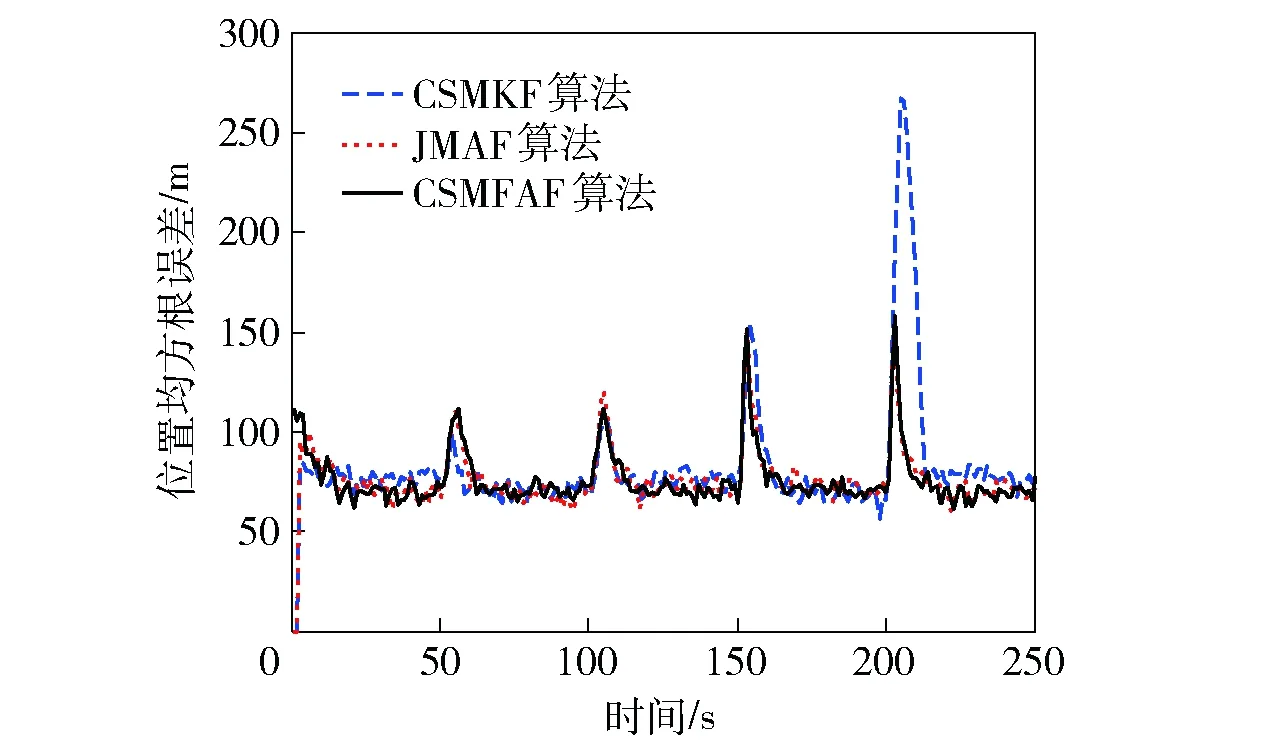
图1 阶跃机动位置均方根误差Fig.1 Root-mean-square errors of step maneuvering position
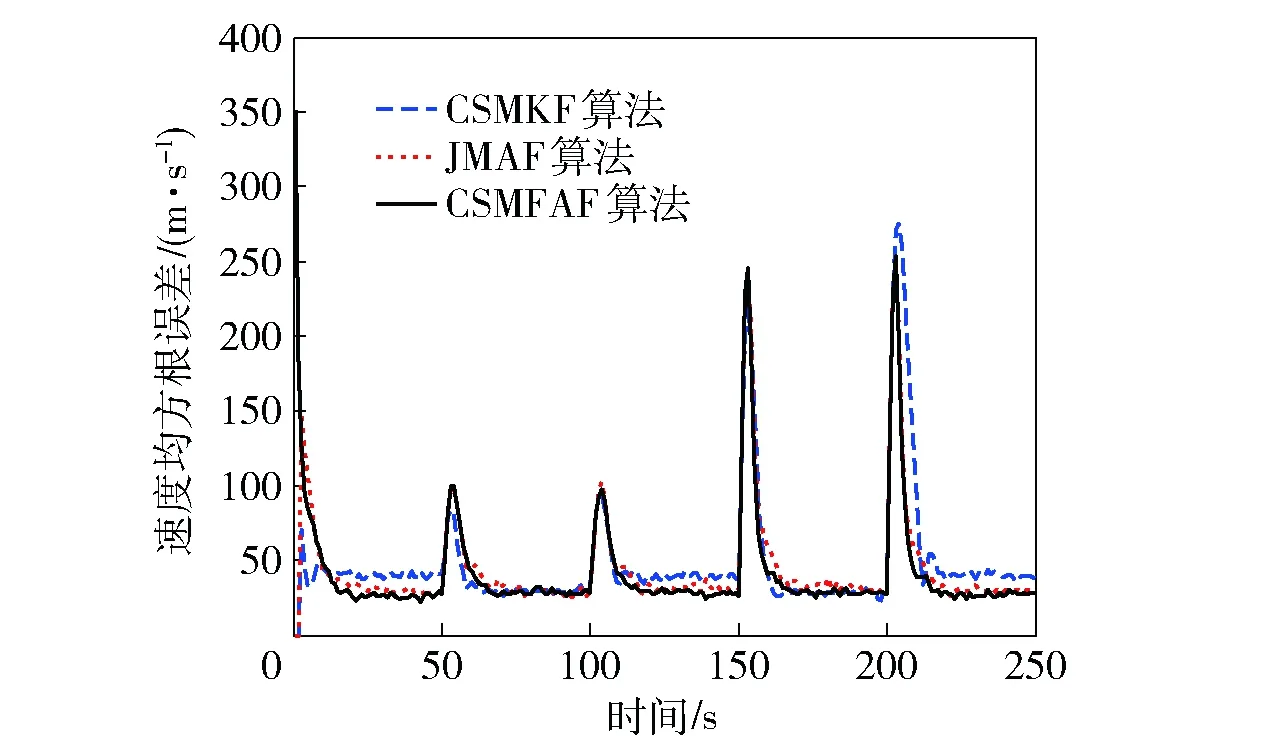
图2 阶跃机动速度均方根误差Fig.2 Root-mean-square errors of step maneuvering speed

图3 阶跃机动加速度均方根误差Fig.3 Root-mean-square errors of step maneuvering acceleration
模拟轨迹2:目标起始沿X轴方向作速度为300 m/s的匀速运动,从第20个扫描周期开始作圆机动运动,向心加速度为3 m/s2,运动半周后恢复匀速运动,30个扫描周期后再次开始作半圆周机动,向心加速度为-6 m/s2,后30个扫描区间恢复匀速运动。仿真结果为图4~图6.
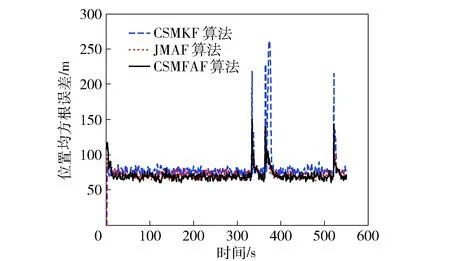
图4 圆周机动位置均方根误差Fig.4 Root-mean-square errors of circular maneuvering position
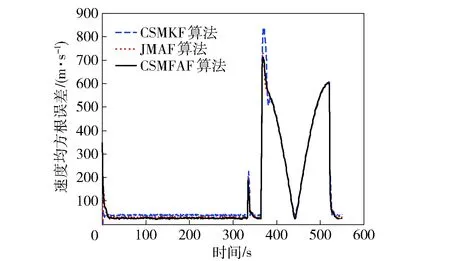
图5 圆周机动速度均方根误差Fig.5 Root-mean-square errors of circular maneuvering speed
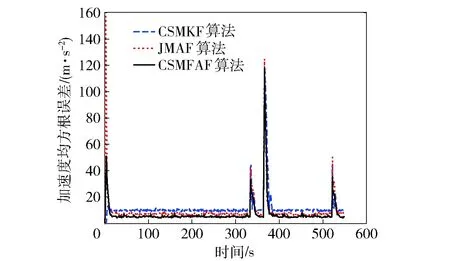
图6 圆周机动加速度均方根误差Fig.6 Root-mean-square errors of circular maneuvering acceleration
模拟轨迹3:目标起始作匀速运动,初速为300 m/s,在第30~150个扫描区间作Jerk机动,在第150~200个扫描区间再作匀速运动。加速度变化率为5 m/s3.
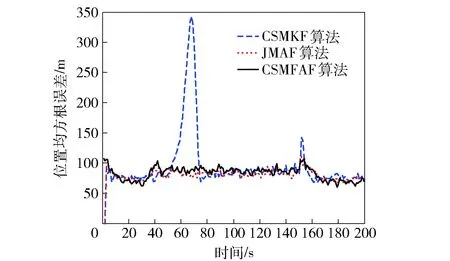
图7 Jerk机动位置均方根误差Fig.7 Root-mean-square errors of Jerk maneuvering position
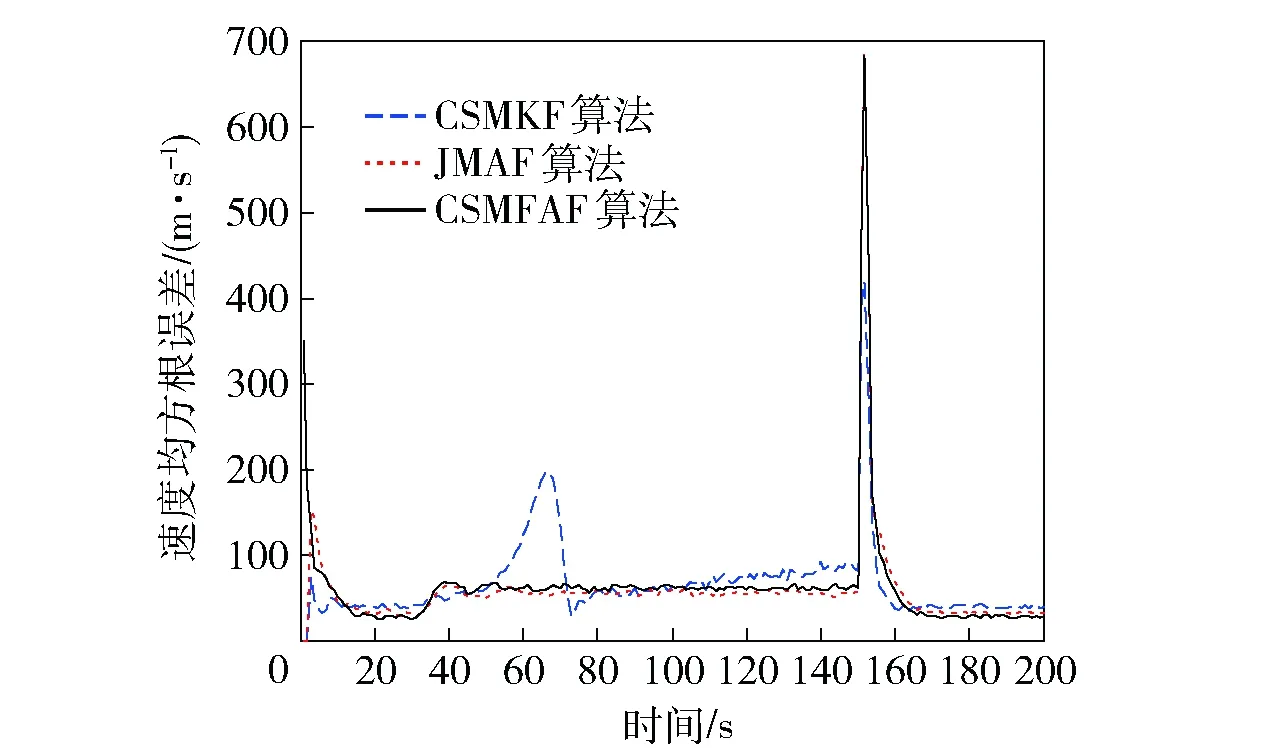
图8 Jerk机动速度均方根误差Fig.8 Root-mean-square errors of Jerk maneuvering speed
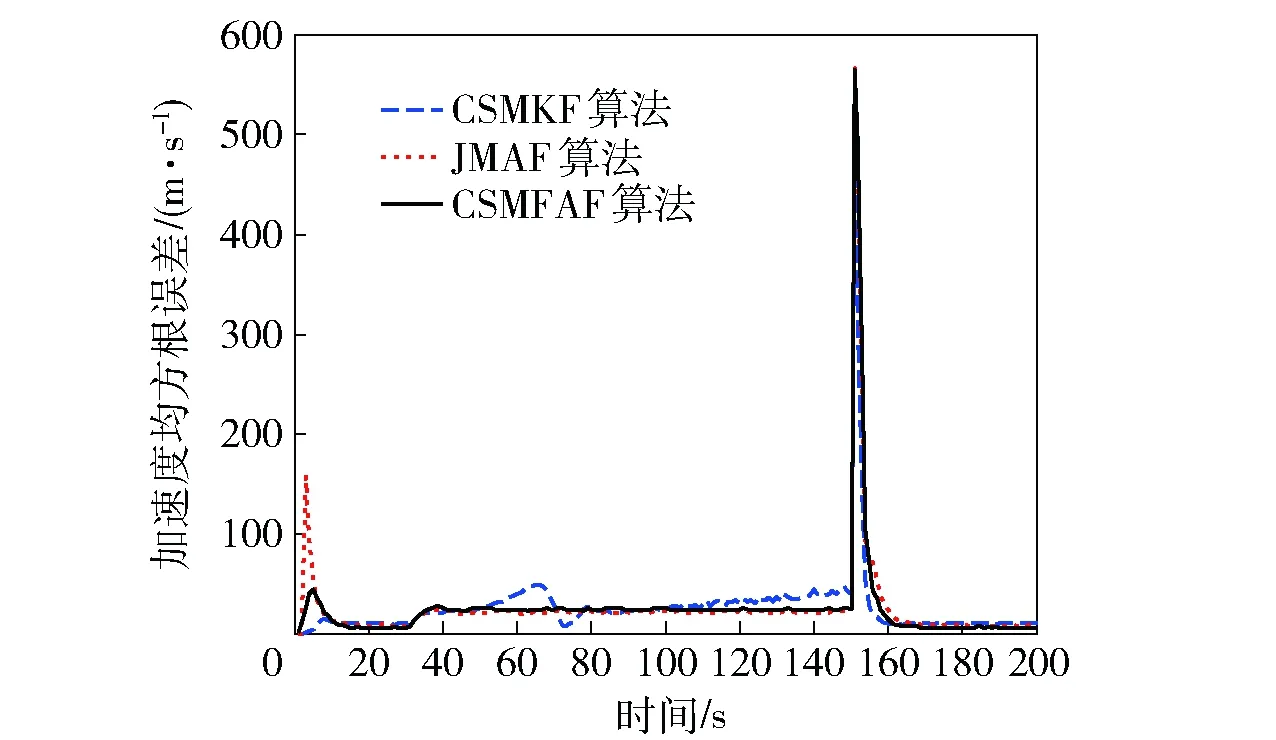
图9 Jerk机动加速度均方根误差Fig.9 Root-mean-square errors of Jerk maneuvering acceleration
3种算法空间和时间复杂度以及运行时间如表2所示,其中n为状态维数,运行时间为计算阶跃机动时250个点的单次仿真时间。不同机动条件下3种算法平均标准位置差(ANPE)[24]如表3所示。

表2 算法性能比较表
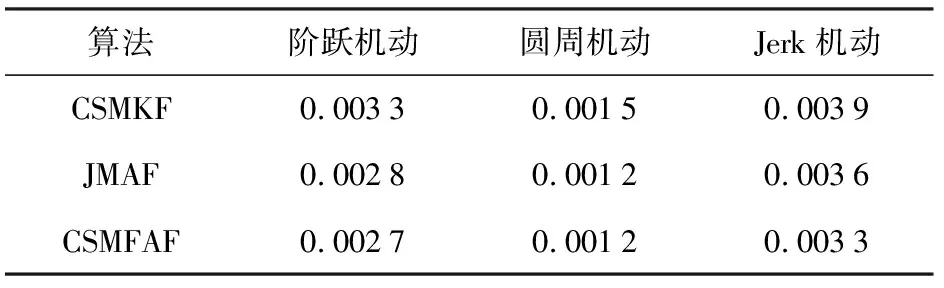
表3 平均标准位置差比较表
3.2 仿真结果及分析
从图1~图3可知:CSMKF算法跟踪第1次阶跃机动时,其峰值误差较小,随着阶跃机动加速度超过给定的最大加速度时,CSMKF算法跟踪性能明显下降,位置和速度均方根误差比其他两种算法要大,动态时延变长;JMAF算法和CSMFAF算法中由于采取了强跟踪和自适应技术,不受给定最大加速度变化率和给定最大加速度的限制,跟踪效果较好,其中在第2次强阶跃机动时,CSMFAF算法的速度和加速度分量收敛速度优于JMAF算法;在匀速和匀加速运动部分,CSMFAF算法和JMAF算法的位置跟踪误差接近,好于CSMKF算法,CSMFAF算法的速度和加速度分量跟踪精度优于其他两种算法。
从图4~图6可知:弱圆周和强圆周机动时,CSMFAF算法跟踪精度和收敛速度好于其他两种算法,说明CSMFAF算法跟踪变加速机动时性能最佳,JMAF算法跟踪性能介于CSMFAF算法和CSMKF算法之间;在两次圆周机动的突变部分,CSMFAF算法和JMAF算法的跟踪误差接近,均好于CSMKF算法。
从图7~图9可看到:Jerk机动区间,3种算法位置跟踪误差接近,JMAF算法的速度和加速度均方根误差略好于CSMFAF算法,CSMKF算法速度和加速度跟踪均方根误差呈发散趋势;在Jerk机动起始和结束时刻,CSMFAF算法和JMAF算法的位置跟踪误差优于CSMKF算法,CSMFAF算法和JMAF算法Jerk机动起始时的速度和加速度跟踪性能比CSMKF算法收敛速度快,结束时由于CSMKF算法速度和加速度分量跟踪效果呈发散趋势,CSMKF算法跟踪误差反而减小;对于较大的阶跃机动,CSMFAF算法位置峰值误差比其他两种算法小,收敛速度快。
由表1可知,3种算法时间复杂度和空间复杂度表达形式相同。CSMFAF算法由于采用模糊推理进行调整,运行时间较长。CSMKF算法由于状态维数少,运行时间最短。由表2可知,在3种典型机动条件下,CSMFAF算法ANPE优于其他两种算法,跟踪圆周机动时ANPE与JMAF算法相等。由于机动性能包括稳态性能和瞬态性能,ANPE只反映了系统跟踪某种机动过程中的平均位置标准差稳态性能。从图5和图6可看出,圆周机动时CSMFAF算法对目标的速度和加速度均方根误差优于JMAF算法。
仿真结果表明,CSMFAF算法能最大限度地利用残差中的有效信息,提高了对强阶跃机动目标的跟踪性能,改善了对弱机动和非机动目标的跟踪精度,减小了动态时延,增强了跟踪系统的鲁棒性和抗干扰能力。
4 结论
提出了当前统计模型模糊自适应算法,通过对机动频率、机动加速度方差和加速度输入的在线调节,实现了当前统计模型的全面自适应,提高了当前模型与机动模式之间的匹配程度。引入高斯隶属函数和强跟踪次优渐消因子对滤波算法进行权值修正,改善了对弱机动和非机动的跟踪精度,增强了对突变机动和变加速机动的跟踪能力。理论分析和文中仿真结果表明,与CSMKF算法和JMAF算法相比,不受机动频率人为给定和最大加速度极值设置的限制,扩大了目标跟踪的范围,不仅具有较好的稳态特性和瞬态特性,还具有较好的实用价值。
References)
[1] Li X R, Jilkov V P. Survey of maneuvering target tracking. PartⅠ: dynamic models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1334-1364.
[2] Tafti A D, Sadati N. A hybrid fuzzy adaptive tracking algorithm for maneuvering targets[C]∥IEEE International Conference on Fuzzy System. Hongkong: IEEE, 2008: 1869-1873.
[3] Naidu V, Raol J R. Performance evaluation of interacting multiple model Kalman filter[J]. IETE Journal of Education, 2008, 49(3): 95-108.
[4] Khaloozadeh H, Karsaz A. Modified input estimation technique for tracking maneuvering targets[J]. IET Proceedings-Radar, Sonar and Navigation, 2009, 3(1): 30-41.
[5] Bahari M H, Pariz N. High maneuvering target tracking using an input estimation technique associated with fuzzy forgetting factor[J]. Scientific Research and Essay, 2009, 4(10): 936-945.
[6] Yang J L, Ji H B. High maneuvering target-tracking based on strong tracking modified input estimation[J]. Scientific Research and Essays, 2010, 5(13): 1683-1689.
[7] Challa S, Morelande M R, Mušicki D, et al. 目标跟踪基本原理[M]. 周共健, 译. 北京: 国防工业出版社, 2015. Challa S, Morelande M R, Mušicki D, et al. Fundamentals of object tracking[M]. ZHOU Gong-jian,translated. Beijing: National Defense Industry Press, 2015. (in Chinese)
[8] Kim H S,Park J G,Lee D. Adaptive fuzzy IMM algorithm for uncertain target tracking[J]. International Journal of Control,Automation,and Systems,2009,7(6):1001-1008.
[9] Wang X H,Yang X Y,Qin Z,et al. Hierarchical interacting multiple model algorithm based on improved current model[J]. Journal of Systems Engineering and Electronics,2010,21(6):961-967.
[10] Mehrotra K,Mahapatra P R. A Jerk model for tracking highly maneuvering targets[J]. IEEE Transactions on Aerospace and Electronic System,1997,33(4) :1094-1105.
[11] 乔向东,王宝树,李涛,等. 一种高度机动目标的当前统计Jerk模型[J]. 西安电子科技大学学报,2002,29(4) :534-539. QIAO Xiang-dong,WANG Bao-shu,LI Tao,et al. A CS-Jerk model for tracking highly maneuvering targets[J]. Journal of Xidian University,2002,29(4) :534-539. (in Chinese)
[12] 周宏仁,敬忠良,王培德. 机动目标跟踪[M]. 北京:国防工业出版社,1991. ZHOU Hong-ren,JING Zhong-liang,WANG Pei-de. Tracking of maneuvering targets[M]. Beijing:National Defense Industry Press,1991. (in Chinese)
[13] Sheng H, Yang J S, Zeng F L, et al. Interacting multiple model tracking algorithm with modified input estimation[J]. Acta Electronica Sinica, 2009, 37(12): 2810-2814.
[14] Qu H Q, Pang L P, LIi S H. A novel interacting multiple model algorithm[J]. Signal Processing, 2009, 89(11): 2171-2177.
[15] 黄长强, 封普文, 曹林平, 等. 状态分量综合修正加速度方差的CSM算法[J]. 西北工业大学学报, 2014, 32(1): 6-11. HUANG Chang-qiang, FENG Pu-wen, CAO Lin-ping, et al. A target tracking algorithm based on current statistical model for adjusting acceleration variance of maneuver target[J]. Journal of Northwestern Polytechnical University, 2014, 32(1): 6-11. (in Chinese)
[16] 周政, 刘进忙, 谭西江. 基于Jerk输入估计的MCS模型及非线性跟踪算法[J]. 北京航空航天大学学报, 2013, 39(10): 1397-1402. ZHOU Zheng, LIU Jin-mang, TAN Xi-jiang. MCS model based on Jerk input estimation and nonlinear tracking algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(10): 1397-1402. (in Chinese)
[17] 刘宝光, 陶青长, 潘明海. 基于当前统计模型的强机动目标跟踪算法[J]. 雷达与对抗, 2012, 32(1): 28-30. LIU Bao-guang, TAO Qing-chang, PAN Ming-hai. An improved tracking algorithm based on current statistical model for highly maneuvering targets[J]. RADAR and ECM, 2012, 32(1): 28-30. (in Chinese)
[18] 袁湛, 瞿军, 董桂旭. 机动频率自适应的机动目标模糊跟踪算法[J]. 战术导弹技术, 2009, 9(2): 56-61. YUAN Zhan, QU Jun, DONG Gui-xu. A maneuvering target fuzzy tracking algorithm with maneuvering frequency adaptive[J]. Tactical Missile Technology, 2009, 9(2): 56-61. (in Chinese)
[19] 朱自谦, 胡士强. 机载雷达多目标跟踪技术[M]. 北京: 国防工业出版社, 2013. ZHU Zi-qian, HU Shi-qiang. Airborne radar multi-target tracking technology[M]. Beijing: National Defense Industry Press, 2013. (in Chinese)
[20] Chan K C C,Lee V,Leung H. Radar tracking for air surveillance in a stressful environment using a fuzzy-gain filter[J]. IEEE Transactions on Fuzzy Systems,1997,5(1):80-89.
[21] 钱广华, 李颖, 骆荣剑. 机动目标跟踪中一种机动频率和方差自适应滤波算法[J]. 雷达学报, 2013, 2(2): 257-264. QIAN Guang-hua, LI Ying, LUO Rong-jian. One maneuvering frequency and the variance adaptive filtering algorithm for maneuvering target tracking[J]. Journal of Radars, 2013, 2(2): 257-264. (in Chinese)
[22] Zhou D H,Frank P M. Strong tracking filtering of nonlinear time-varying stochastic systems with colored noise:application to parameter estimation and empirical robustness analysis[J]. International Journal of Control,1996,65(2):295-307.
[23] 范小军, 刘锋, 秦勇, 等. 基于STF的当前统计模型及自适应跟踪算法[J]. 电子学报, 2006, 34(6): 981-984. FAN Xiao-jun, LIU Feng, QIN Yong, et al. Current statistic model and adaptive tracking algorithm based on strong tracking filter[J]. Acta Electronica Sinica, 2006, 34(6): 981-984. (in Chinese)
[24] 刘望生, 李亚安, 崔琳. 高度机动目标Jerk模型及改进算法[J]. 兵工学报, 2012, 33(4): 385-389. LIU Wang-sheng, LI Ya-an, CUI Lin. A modified algorithm for high maneuvering target based on Jerk model[J]. Acta Armamentarii, 2012, 33(4): 385-389. (in Chinese)
A Fuzzy Adaptive Algorithm for Maneuvering Target Based on Current Statistical Model
LIU Wang-sheng1, PAN Hai-peng1, LI Ya-an2
(1.School of Mechanical Engineering and Automation, Zhejiang Sci-Tech University, Hangzhou 310018, Zhejiang, China; 2.School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, Shaanxi, China)
A fuzzy adaptive algorithm is proposed for the imperfections of tracking a maneuvering target using conventional algorithm based on current statistical model. Maneuvering frequency is adjusted in real time by fuzzy reasoning according to the normalized residual and its change rate. Acceleration variance is depicted using residual power function, and the mean value of current acceleration is updated by the deviation between the estimated and predicted values of acceleration. On this basis, the weight of proposed algorithm is revised by Gauss membership function and strong tracking algorithm. Fuzzy adaptive algorithm is not restricted by maneuvering frequency given manually and extreme value of maximum acceleration, which is suitable for the different ranges and degrees of maneuvering. The performance of the proposed algorithm is tested by tracking three typical maneuvering targets, such as step maneuvering, circular maneuvering, and Jerk maneuvering. Simulated results show the tracking range is expanded using the proposed algorithm compared with the conventional tracking algorithm based on current model and the adaptive algorithm based on Jerk model. The proposed algorithm has good steady-state and transient characteristics, and its tracking accuracy and convergence rate are superior to those of the other two algorithms.
ordnance science and technology; current statistical model; Jerk model; fuzzy adaptive filtering; strong tracking; maneuvering target
2016-03-17
国家自然科学基金项目(51179158); 浙江理工大学科研基金项目(1202803-Y)
刘望生(1974—), 男, 副研究员。E-mail: lwsh22@hotmail.com
TN929.3
A
1000-1093(2016)11-2037-07
10.3969/j.issn.1000-1093.2016.11.011

