面向火炮射击密集度的随机因素稳健设计
王丽群, 杨国来, 刘俊民, 葛建立
(1.南京理工大学 机械工程学院, 江苏 南京 210094;2.内蒙古北方重工业集团有限公司, 内蒙古 包头 014033)
面向火炮射击密集度的随机因素稳健设计
王丽群1, 杨国来1, 刘俊民2, 葛建立1
(1.南京理工大学 机械工程学院, 江苏 南京 210094;2.内蒙古北方重工业集团有限公司, 内蒙古 包头 014033)
为了实现对射击密集度的有效控制,解决考虑随机因素的射击密集度优化设计问题,利用基于随机模型和随机优化的稳健设计理论,提出一种指标要求导向型的随机因素参数区间计算方法。基于蒙特卡洛模拟,采用六自由度外弹道模型,利用某型大口径榴弹炮数据求解射击密集度并研究其统计特性。利用不合格概率、灵敏度指数两个稳健目标准则,构建射击密集度稳健设计随机模型。采用带精英策略非支配排序遗传算法并结合反向传播神经网络代理模型技术对稳健设计随机模型进行优化求解,确定符合指标要求的随机因素参数区间。对比分析结果表明,该方法可同时保证射击密集度指标的最优性和稳健性,对射击密集度的预测具有一定可行性。
兵器科学与技术; 射击密集度; 稳健设计; 随机因素; 多目标遗传算法; 神经网络
0 引言
射击密集度是火炮武器系统的重要战术技术指标,也是射击精度的重要组成部分。在火炮武器系统研制过程中,经常发生射击密集度达不到指标要求的情况,这主要是因为不能有效地控制影响射击密集度的设计参量。而射击密集度是一个涉及弹、炮、药、气象环境等众多因素的系统问题,弹丸起始扰动、弹药误差、气象条件等都将影响射击密集度,并且这些因素是典型的随机因素,均在一定的误差范围内随机变化。因此,找到最佳的随机参数组合,确定各随机因素的合理参数区间,可以为火炮关键结构参数优化设计以及弹药的加工提供理论参考,进而在火炮的总体设计阶段掌握影响射击密集度的设计因素,实现对射击密集度的有效控制。
目前对于火炮射击密集度的研究大多集中在以炮口扰动为目标[1-2]的发射动力学分析,而研究火炮发射全过程中随机因素较少。对于随机因素的影响分析,曹宁等[3]研究了弹丸初速、弹丸质量和弹丸偏心距等因素对车载炮射击密集度的影响,建立了影响程度逐步回归分析算法。吴宏等[4]采用均匀设计与逐步回归结合的方法分析了弹炮间隙、质量偏心、动不平衡角、发射药量、挤进压力、弹丸质量和风速对射击密集度的影响。现有对射击密集度的处理,均是采用误差合成或多次计算取均值的方法,将射击密集度这一随机模型转化为确定性模型求解,随机变量或射击密集度的随机性没有得到很好体现。同时,现有射击密集度随机因素的研究均不涉及参数优化设计,无法根据指标要求直接计算给出合适的、富有理论依据的参数区间。针对以上问题,本文从“弹丸出炮口运动散布—射击密集度”过程出发。采用基于随机模型和随机优化的稳健设计理论,先构建射击密集度随机模型,再采用带精英策略非支配排序遗传算法(NSGA-Ⅱ)并结合反向传播(BP)神经网络对随机模型进行优化求解,确定了符合指标要求的随机因素参数区间,探讨了考虑随机因素的射击密集度优化设计问题。
1 稳健设计基本思想
稳健设计的基本思想是在已知输出空间下,找出最合适的输入空间,使产品的质量特性既限定在给定的输出空间内,它的均值又与目标值的差异为最小[5-6]。对于含有随机因素的随机问题,输入空间指随机设计变量的均值μx及其容差Δx-、Δx+. 若随机设计变量服从正态分布,则输入空间为其均值μx和标准差σ. 图1展示了稳健优化设计解与一般优化设计解的区别,其中gi(i=1,2,…,n)为随机性约束函数,ai(i=1,2,…,n)为预先设定应满足的概率值。

图1 稳健设计最优解Fig.1 Optimal solution for robust design of random model
2 射击密集度稳健设计随机模型构建
2.1 随机因素的分类、选取与随机性
工程实际中,随机因素可以根据其不同特点分为可控因素和不可控因素两类。可控因素也称随机设计变量,是指在实际中可以控制均值和容差的改变减小输出特性的波动和偏差的因素。数学表示为
xT=(x1,x2,…,xn)∈(Ω,ζ,P)⊂Rn.
(1)
不可控因素也称随机参数,是指对输出特性有影响,而在实际操作中难以人为控制的因素,例如使用条件、操作人员、环境因素等。数学表示为
zT=(z1,z2,…,zk)∈(Ω,ζ,P)⊂Rk.
(2)
(1)式、(2)式中:x为n维随机设计变量;z为k维随机参数;(Ω,ζ,P)为概率空间,Ω为随机事件,ζ为事件的全体,P为事件发生的概率,表示x和z都是属于概率空间的向量。
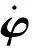
对射击密集度有影响的随机因素描述为某种概率分布近似描述其随机特性。在缺乏必要的统计试验数据时,随机设计变量假定为正态分布,并以随机因素的均值μx和标准差σx作为设计变量,根据正态分布“3σ”原则抽取随机数[7]。在本文的研究中,主要选用正态分布和随机分布两种分布类型,各随机因素的具体概率分布类型见表1.

表1 随机因素概率分布类型
2.2 射击密集度的计算与随机性分析
为了获得射击密集度的随机分布类型,以某型大口径榴弹炮数据编写射击密集度计算程序,并采用一组数据重复计算1 500次,对纵向密集度EX与横向密集度EZ进行统计分析。
表2、图2和图3的统计结果是基于蒙特卡洛法模拟的计算方法,采用六自由度外弹道模型[8],利用计算机随机抽样的方法求得的射击密集度数据统计平均值。
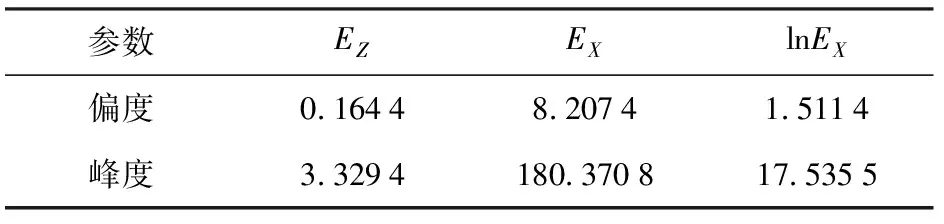
表2 数据分布统计表

图2 横向密集度EZ统计分布直方图Fig.2 Statistical distribution histogram of EZ
表2中的偏度与峰度分别指样本数据标准化变量的3阶、4阶中心矩。偏度反映分布的对称性,接近0则认为分布是对称的;峰度亦是衡量偏离正态 分布的尺度,正态分布的峰度为3. 图2、图3中的红线表示以该组射击密集度数据的均值与标准差构建的正态分布曲线。
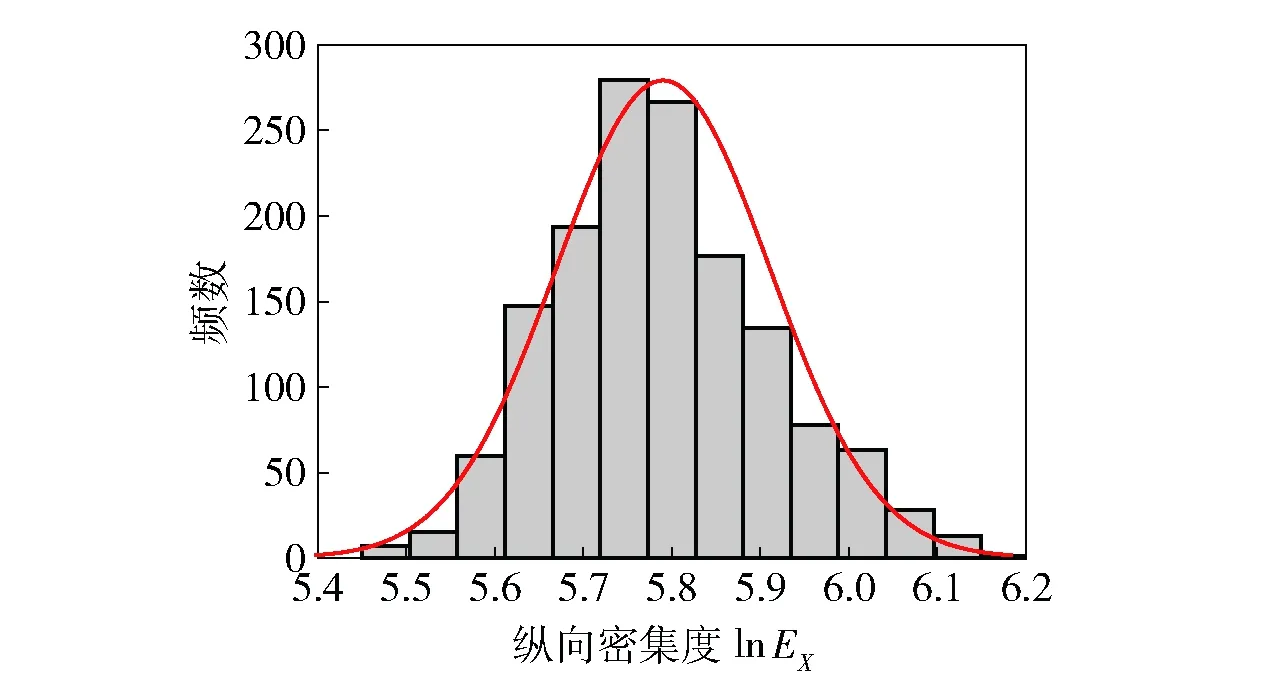
图3 纵向密集度lnEX统计分布直方图Fig.3 Statistical distribution histogram of lnEX
由表2和图2可以看出,横向密集度服从正态分布;由表2和图3可见,纵向密集度样本数据的对数近似服从正态分布,即服从对数正态分布。在确定射击密集度的分布类型后,可以通过多次重复计算求解射击密集度的分布参数(均值、方差),确定其概率密度函数并在稳健设计中使用。
2.3 射击密集度稳健设计目标准则


(3)
式中:q为指标个数。P{·}∈(0,1)的数值越小,则不合格率越小,说明输出特性越稳定。
目标准则之二是灵敏度指数SI. 由于在工程实际中,希望每一项技术特性的实际值与目标值的差异尽量小,即希望输出特性更加优质[7],因此采用灵敏度指数SI衡量输出特性的优质性,使

(4)
式中:μyj为yj的统计均值,当μyj=yoj时,SI=0.
概率P的计算方法主要有随机模拟法、数值积分法和1次2阶矩法等,本文采用数值积分法进行求解。依托某型大口径榴弹炮数据,设定纵向密集 度目标值EX=1/yX=1/350,同时设定容差ΔyX为20;设定横向密集度目标值EZ=yZ=0.6 mil,由于横向密集度一般符合指标要求,因此放大容差设定,ΔyZ为0.3 mil. 在每次稳健设计中,为了兼顾计算精度与求解速度,对一组随机设计变量重复计算100次,计算获得EX和EZ的均值μEX、μEZ与标准差σEX、σEZ,根据2.2节求得纵向密集度与横向密集度的分布类型,代入(5)式中,获得EX和EZ的概率密度函数。
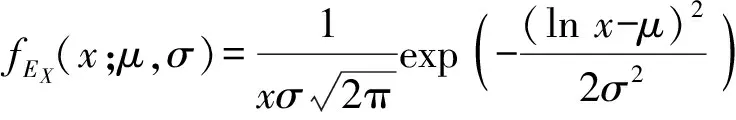
(5)
由于正态分布与对数正态分布均不可积,因此通过(6)式高斯—洛巴托积分方法,求解EX和EZ概率密集函数的4次等效积分,计算不合格概率P.

(6)
式中:xk为积分节点坐标;Ak为积分系数;n为积分所用项数。
由于积分区间不是[-1,1],因此按照(7)式先行转换积分区间。
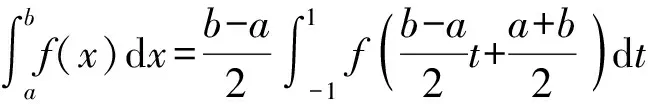

(7)
通过(4)式的定义计算灵敏度指数SI.
3 基于多目标遗传算法的随机模型优化
采用模拟搜索算法对随机模型进行优化是随机变量优化设计的一种简便有效的方法。本文采用NSGA-II多目标遗传算法对射击密集度稳健设计随机模型进行优化,即通过对设计变量的随机模拟搜索,寻找稳健设计的最优解,以确定最佳参数组合和各随机因素参数区间。NSGA-II多目标遗传方法基于Pareto最优概念,是一种启发式模拟搜索算法,其采用非支配排序过程、精英保留策略和无参数小生境操作算子[9-10],可以获得设计变量的最优解集。但由第2节可知,每次稳健设计构建随机模型的过程需要调用射击密集度计算程序进行一定数量的随机模拟,然后进行约束准则与目标准则的求解。为了保证计算精度,重复计算次数很大,产生巨大计算费用而不便用于后序优化。为了提高计算效率,采用基于代理模型的优化策略。本文的研究中选用BP神经网络,它具有良好的学习能力和非线性映射能力,一个3层的BP神经网络可以任意逼近复杂的非线性函数。
3.1 优化设计变量与优化数学模型
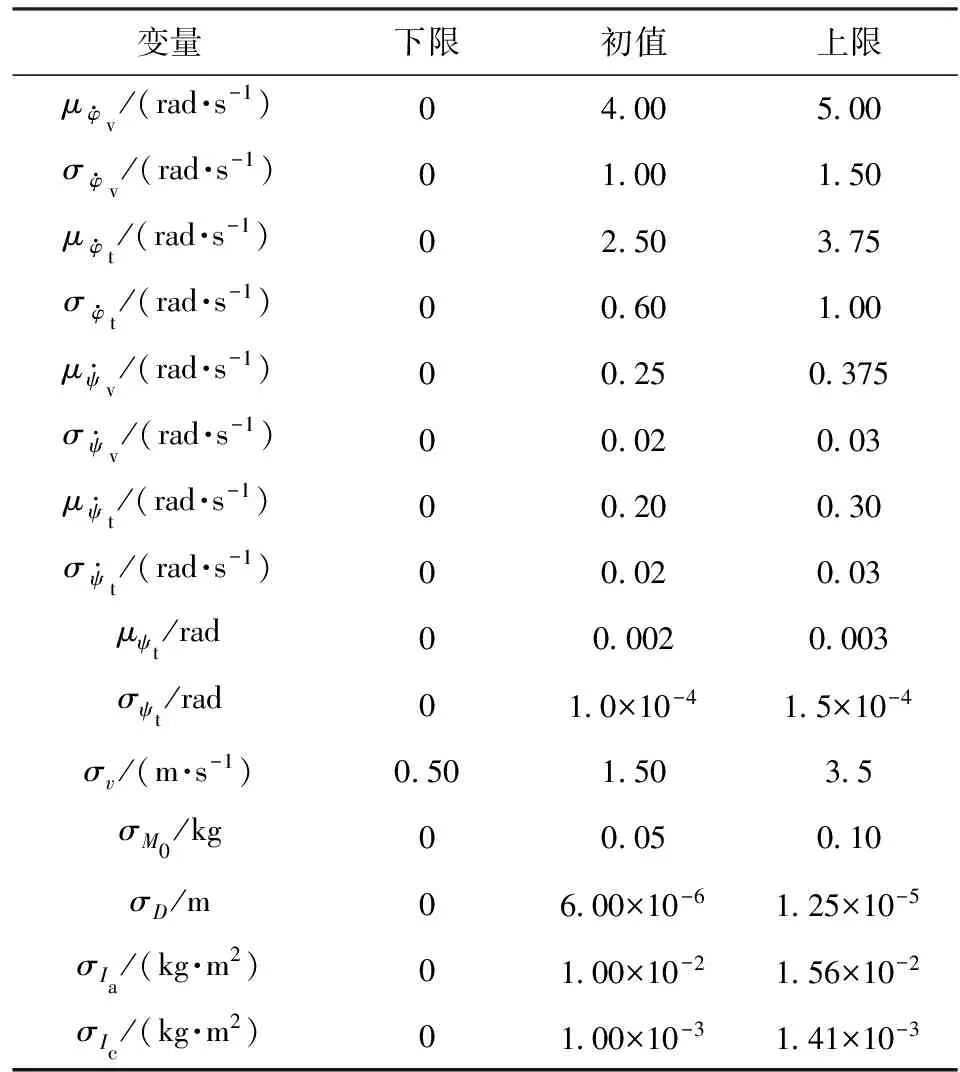
表3 随机设计变量及取值范围
基于射击密集度稳健设计随机模型,建立以弹丸起始扰动参数和弹丸结构参数误差为随机设计变量,以射击密集度指标要求为约束条件,稳健目标准则为优化目标的数学模型为

s.t.
(8)
3.2 BP神经网络代理模型构建与可信度评估
参见图4,本文构造BP神经网络代理模型经过3个步骤:首先依托某型大口径榴弹炮数据,采用最优拉丁超立方试验设计安排1 000组试验样本;然后代入射击密集度稳健设计随机模型中,得到不合格率P、灵敏度指数SI、纵向密集度均值EX、横向密集度均值EZ作为输出,获得输入到输出的训练样本;利用Matlab神经网络工具箱训练一个3层的BP神经网络。
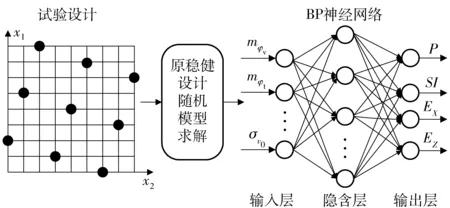
图4 BP神经网络代理模型构建过程Fig.4 Model building process of BP neural network
为了提高训练精度,在训练前进行样本数据的归一化处理,消除各设计变量量纲与量级之间的差别。输入层节点数设为15,隐含层节点数经反复试算设定为30,其传递函数采用tansig函数;输出层节点数为4,其传递函数采用purelin函数。采用精度较高的trainlm训练函数和learngdm学习函数对神经网络进行训练。
采用最优拉丁方试验设计生成100组验证样本,带入原射击密集度稳健设计随机模型中获得相应输出,计算确定性系数R2检验神经网络模型可信度。
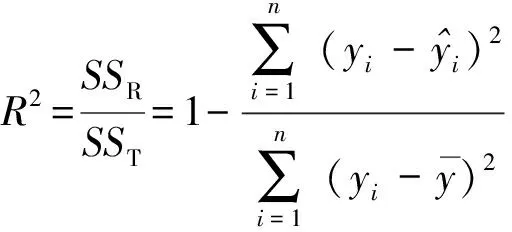
(9)


表4 神经网络可信度检验
3.3 优化结果与分析
优化计算得到随机设计变量的Pareto最优解集,优化结果的Pareto前沿如图5所示。

图5 优化结果Pareto前沿Fig.5 Pareto front
由图5可见,Pareto前沿中的设计点,稳健目标准则均得到不同程度的优化。Pareto前沿左侧的设计P较小,输出特性较为稳定;右侧的设计SI较小,输出特性更加优质;中部的设计较为折中。在Pareto前沿的左、中、右侧分别选择一组设计方案,即图5中A、B、C设计点,以使选择的方案具有代表性。带入原射击密集度稳健设计模型中进行详细的分析计算,并与采用遗传算法优化(不含稳健设计)得到的普通优化结果进行对比,计算结果见表5.

表5 不同设计的对比
由表5可知,基于随机模型与随机优化的稳健设计得到的3组优化结果虽不相同,但都可以满足预先设定的射击密集度EX=1/350、EZ=0.6 mil的指标要求。基于遗传算法未经稳健设计的普通优化结果,在均值上可以满足EX=1/350的目标,但偏离目标程度较大,这意味着无法实现精确的设计;过高的指标意味着过高的技术成本,这也不是我们所希望的;同时稳健性较差,计算结果必将不稳定。需要特别指出的是,表5中目标准则SI变化规律满足图5,目标准则P与图5有一定差异,这一方面是代理模型精度造成的,另一方面由于3组设计均满足约束条件,Pareto前沿中稳健目标准则P结果相差并不明显,约为0.005左右,这种差异是可接受的。
兼顾不合格概率P和灵敏度指数SI两个稳健目标准则,选择C设计点作为最终的设计,从而确定纵向密集度EX=1/350、横向密集度EZ=0.6 mil时各随机因素的参数区间,数据圆整后如表6所示。
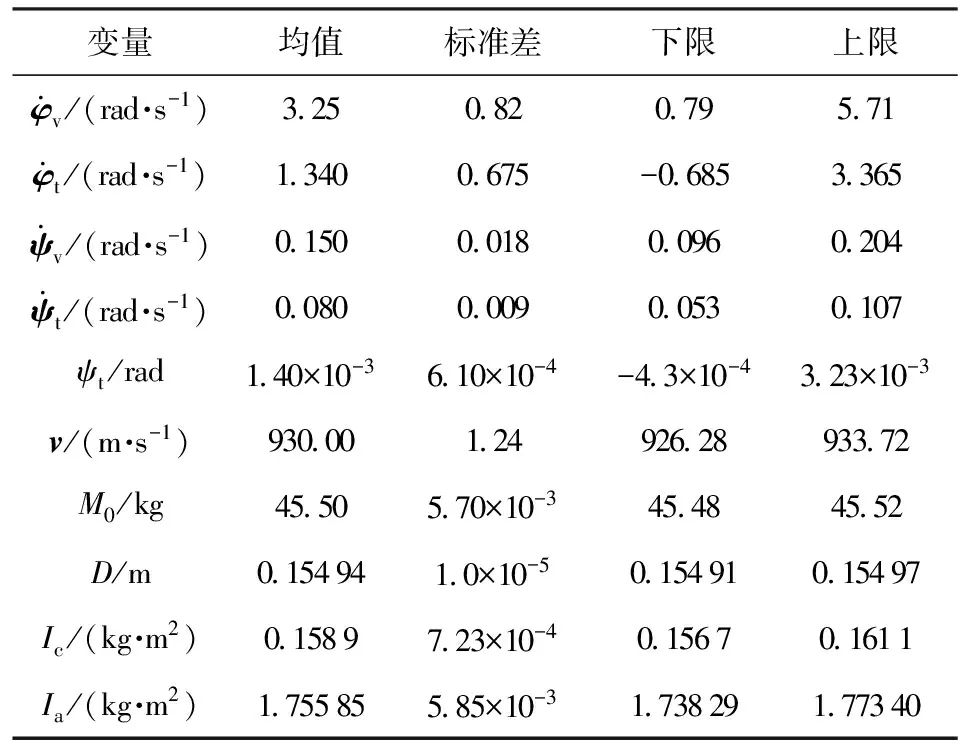
表6 随机因素参数区间优化结果
相似的,可以根据工程射击密集度指标需要,设定不同的目标,例如纵向密集度EX为1/300、1/400,采用相同的方法就可以获得不同指标下的随机因素参数区间。
4 结论
本文从“弹丸出炮口运动散布- 射击密集度”过程出发,采用基于随机模型和随机优化的稳健设计理论,探讨了考虑随机因素的射击密集度优化设计问题,以某型大口径榴弹炮为例初步验证了该方法的有效性。
目前仅研究了火炮发射过程的一个阶段,若将该方法进一步扩展到火炮关键结构参数误差,从理论上揭示其与射击密集度的传递机理及影响关系,将在总体设计阶段实现对射击密集度的有效控制。另一方面,火炮发射过程中的随机因素目前尚缺乏相关统计试验数据,未来若从试验角度揭示随机因素的分布类型,引入更加完整的气象模型与数据,计算结果将更加准确。
References)
[1] 梁传建, 杨国来, 王晓锋. 基于神经网络和遗传算法的火炮结构动力学优化[J]. 兵工学报, 2015, 36(5): 789-795. LIANG Chuan-jian, YANG Guo-lai, WANG Xiao-feng. Structural dynamics optimization of gun based on neural networks and genetic algorithms[J]. Acta Armamentarii, 2015, 36(5): 789-795. (in Chinese)
[2] 谢润, 杨国来. 自行高炮行进间射击炮口响应特性研究[J]. 兵工学报, 2014, 35(8): 1158-1163. XIE Run, YANG Guo-lai. Research on response characteristics of muzzle for self-propelled antiaircraft gun firing on the move[J]. Acta Armamentarii, 2014, 35(8): 1158-1163. (in Chinese)
[3] 曹宁, 王晓锋, 徐亚栋, 等. 基于逐步回归法的车载炮射击精度影响因素分析[J]. 南京理工大学学报, 2013, 37(4): 557-560. CAO Ning, WANG Xiao-feng, XU Ya-Dong, et al. Evaluation of influencing factors on firing accuracy of wheeled artillery based on stepwise regression analysis[J]. Journal of Nanjing University of Science and Technology, 2013, 37(4): 557-560. (in Chinese)
[4] 吴宏, 赵有守. 随机因素对弹丸射击精度影响的分析方法[J]. 弹箭与制导学报, 2001, 21(3): 56-59. WU Hong, ZHAO You-shou. A method to study fire precision of projectile effected by random factors[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2001, 21 (3): 56-59. (in Chinese)
[5] 申立娟, 杨军, 赵宇. 基于方差传递模型的飞机蒙皮拉形工艺稳健设计[J]. 机械工程学报, 2011, 47(1): 145-151. SHEN Li-juan, YANG Jun, ZHAO Yu. Robust design of aircraft skin stretch forming process based on transmitted variance model[J]. Journal of Mechanical Engineering, 2011, 47(1): 145-151. (in Chinese)
[6] Huang B Q, Du X P. Analytical robustness assessment for robust design[J]. Structural and Multidisciplinary Optimization, 2007, 34(2): 123-137.
[7] 陈立周. 稳健设计[M]. 北京: 机械工业出版社, 2000:255-263. CHEN Li-zhou. Robust design[M]. Beijing: China Machine Press, 2000: 255-263. (in Chinese)
[8] 郭锡福. 远程火炮武器系统射击精度分析[M]. 北京: 国防工业出版社, 2004: 38-60. GUO Xi-fu. Firing accuracy analysis for long range gun weapon systems[M]. Beijing: National Defense Industry Press, 2004: 38-60. (in Chinese)
[9] 蔡云骧, 周志勇, 徐小倩, 等. 一种基于精英策略非支配排序遗传算法-Ⅱ的多层吸波涂层结构设计方法[J].兵工学报, 2015, 36(8): 1574-1579. CAI Yun-xiang, ZHOU Zhi-yong, XU Xiao-qian, et al. A design method for multilayered microwave absorbing coating structure based on NSGA-II[J]. Acta Armamentarii, 2015, 36(8): 1574-1579. (in Chinese)
[10] 钱辉仲, 顾克秋, 彭迪, 等. 基于NSGA-II算法的超轻型火炮摇架多目标优化设计[J]. 机械设计, 2012, 29(6): 36-39. QIAN Hui-zhong, GU Ke-qiu, PENG Di, et al. Multi- objective optimization design of ultralightweight artillery cradle based on NSGA-II algorithm[J]. Journal of Machine Design, 2012, 29(6): 36-39. (in Chinese)
Robust Design of Random Factors on Gun Firing Dispersion
WANG Li-qun1, YANG Guo-lai1, LIU Jun-min2, GE Jian-li1
(1.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China; 2.Inner Mongolia North Heavy Industries Group Co., Ltd.,Baotou 014033,Inner Mongolia,China)
To study the effective ways to improve the firing dispersion and solve its optimal design problem considering random factors, a calculation method of parameters interval oriented by the predefined indicators is proposed by using robust design theory based on random model and random optimization. A large caliber howitzer data is used to calculate firing dispersion based on Monte Carlo simulation and six degrees of freedom exterior ballistics model, and the statistical properties of firing dispersion are analyzed. A random model of robust design is built by calculating the objective criteria of robust design including unqualified probability and sensitivity index. Based on multi-objective genetic algorithm (NSGA-II) and BP neural network, the random model is optimized to determine the parameters interval of random factors which meet the requirements. The analysis results show that the proposed method can ensure the optimality and robustness of firing dispersion, and is feasible for the prediction of firing dispersion.
ordnance science and technology; firing dispersion; robust design; random factor; multi-objective genetic algorithm; neural network
2016-05-13
国家“973”计划项目(6132490303);国家自然科学基金项目(11572158);中央高校基本科研业务费专项资金项目(30915118825)
王丽群(1992—),男,博士研究生。E-mail:lqwangnjust101@163.com; 杨国来(1968—),男,教授,博士生导师。E-mail:yyanggl@mail.njust.edu.cn
TJ301
A
1000-1093(2016)11-1983-06
10.3969/j.issn.1000-1093.2016.11.003

