带零吸收项的变步长l0范数归一化最小均方误差算法
管四海, 李智, 黄辉, 王哲
(1.西安电子科技大学 机电工程学院, 陕西 西安 710071; 2. 西安电子科技大学 电子工程学院, 陕西 西安 710071; 3.西安航天动力测控技术研究所, 陕西 西安 710025)
带零吸收项的变步长l0范数归一化最小均方误差算法
管四海1, 李智1, 黄辉2, 王哲3
(1.西安电子科技大学 机电工程学院, 陕西 西安 710071; 2. 西安电子科技大学 电子工程学院, 陕西 西安 710071; 3.西安航天动力测控技术研究所, 陕西 西安 710025)
针对稀疏系统的识别问题,提出一种带零吸收项的变步长l0范数约束归一化最小均方误差 (l0-NLMS)算法。在此改进的l0-NLMS算法中,通过箕舌函数来调整步长的变化,理论推导了此l0-NLMS算法在均值和均方差下的收敛条件以及均方误差和均方偏移量的表达式。设计实验分别比较在不同输入信号时算法的步长和稳态偏移量的变化,通过仿真验证该算法在识别稀疏信道模型上是有效的。分析结果表明:当处于相对高的信噪比、低的信噪比、输入不相关信号和输入相关信号时,该算法具有较快的收敛速度,能很好地进行稀疏系统的模型识别。
信息处理技术; 稀疏系统;l0范数约束归一化最小均方误差算法; 变步长; 系统噪声; 箕舌函数
0 引言
最小均方误差(LMS)算法简单易行,故在系统识别、噪声去除以及信道估计等方面已得到广泛的应用[1]。虽然自适应信道估计(ACE)能有效地估计稀疏信道[2-3],但步长决定ACE的性能,包括算法的收敛速度、计算量等[4]。步长较大时自适应算法具有较快的收敛速度,但同时会带来很大的最小均方误差(MSE),甚至使得算法无法收敛。虽然小的步长会降低MSE,但随之会降低收敛速度,故在实际中希望在开始阶段选择大的步长,使自适应算法有较快的速度去收敛;当自适应算法趋于稳定时,选较小的步长,使其具有较小的MSE. 显然,固定步长的算法不能很好均衡收敛速度和稳态误差二者的矛盾,因此很多学者从变步长的角度研究LMS算法[5-16]。文献[5]提出变步长LMS(VSSLMS)算法,尽管VSSLMS算法能获得较小的稳态误差,但是权系数调整步长在更新时易受噪声影响。针对此问题,文献[6]提出一种解决方法,但在环境突变时此方法的跟踪性能较差。文献[8]提出函数控制的变步长LMS(FCVSSLMS)算法,它能确保在大多时间内算法具有大的收敛速度。稀疏系统不同于一般系统,在很多实际场景中假设系统的系数大多数为0或接近于0[2,9],故一旦一般的LMS算法应用到稀疏系统时,这些算法效果不佳。文献[7]提出更稳健的变步长LMS(MRVSSLMS)算法,可有效解决文献[4]存在的问题。但若应用的系统是稀疏系统,此时算法的收敛性能会变坏。文献[17]在Gu等[10]提出零吸收项的LMS(ZALMS)算法的基础上,给出了改进的零范数约束LMS(l0_LMS)算法,但此算法中误差也易受噪声干扰且权系数调整步长因子还待修正。针对此,文献[18]提出一种改进的l0_LMS算法。Chen等[11]基于文献[10]提出了再加权的ZALMS(RZALMS)算法,然而在RZALMS算法中对零吸引因子的选择不灵活。针对此问题,文献[19]提出了一种改进的RZALMS算法。为克服l0和l1范数约束的最小均方算法在不同信道稀疏程度下对稀疏信道估计中出现的收敛性能起伏较大等缺点,文献[20]提出一种新的似p范数约束的最小均方算法,能很好地估计水声信道[3]。文献[10]在FCVSSLMS 算法基础上提出一种新的算法,但是在更新步长时系统噪声的影响是个亟需解决的问题。为了消除系统噪声在补偿调整时的影响,文献[13]在文献[14]基础上提出改进的变步长NLMS(IVF-NLMS)算法,但当系统稀疏度降低时算法性能降低。针对此问题,文献[12]提出一种算法,然而针对输入为相关信号,如何提高算法收敛速度和在识别稀疏系统时的抗噪声性能,有待进一步改进,且算法的稳定性易受输入信号的影响。
综上分析,本文提出一个改进的l0范数约束NLMS算法,该算法的步长由箕舌函数控制更新。分析结果表明:在不同的信噪比以及不相关或相关的输入信号下,本文算法有较快的收敛速度和识别性能。
1 本文算法及分析
1.1 算法阐述
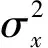
d(n)=XT(n)Wo+ζ(n),
(1)
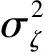
标准LMS算法的代价函数表示为
W(n)=arg minJ(W(n))=arg min|e(n)|2,
(2)
e(n)=d(n)-XT(n)W(n).
(3)
在原J(W(n))上附加一个l0约束项,形如(4)式:
J(W(n))=|d(n)-XT(n)W(n)|2+
γ(n)‖W(n)‖0,
γ(n)=λμ(n),
(4)
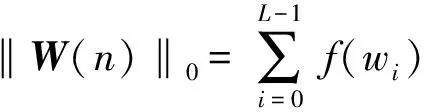
(5)
(6)
式中:γ(n)>0是权衡约束项‖W(n)‖0和|d(n)-XT(n)W(n)|2;μ(n)为步长;λ为均衡量,用于均衡收敛速度和稳态误差二者之间的矛盾。
用梯度法解(2)式,对J(W(n))求梯度得[10]
γ(n)fλ(W(n)),
(7)
(8)
因此可得系统系数的更新求解式:
γ(n)fλ(W(n)),
(9)
式中:δ为很小的正数,确保(9)式成立,即防止XT(n)X(n)=0.
为了动态调整μ(n),本文采用一个基于箕舌函数[15-16]的变量来动态改变步长μ(n):

(10)
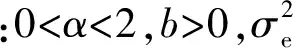
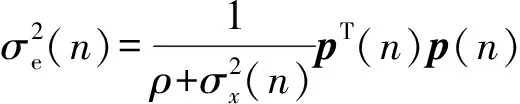
(11)
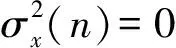
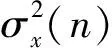
(12)
式中:1-1/(2L)≤χ<1[21]。
故综上所述,(3)式、(9)式、(10)式、(11)式、(12)式就构成了本文提出的改进带零吸收项的l0-NLMS算法。
1.2 算法性能分析
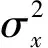
把z(n)=W(n)-Wo代入(9)式,可得
γ(n)fλ(W(n))-Wo.
(13)
把(3)式代入(13)式,得z(n+1)的递推表达式:
z(n+1)=z(n)+
γ(n)fλ(W(n)).
(14)
把(1)式代入(14)式,得
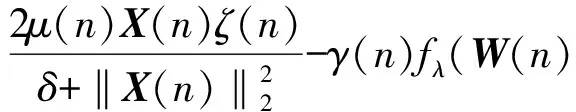
(15)
1.2.1 均值收敛
可用(15)式得到所提算法均值意义下的收敛性能,对(15)式两端取期望,得
E[z(n)]-λE[μ(n)fλ(W(n))].
(16)
设λmax是R的最大的特征值,显然λmax≤tr(R)。tr(·)表示求迹运算。因此提出的算法在均值意义下收敛的条件为
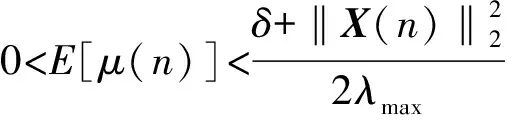
(17)
当n→∞时,
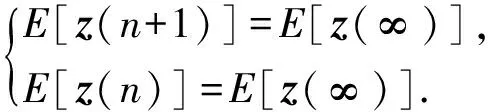
(18)
把(18)式代入(16)式,得

(19)
结合(8)式与假设条件化简(19)式,得
E[z(∞)]=
(20)
把(20)式代入z(n)=W(n)-Wo,可得在稳态时系数均值的表达式:
E[W(∞)]=
(21)
1.2.2 稳态均方偏移量
本节中将给出本文所提出稳态均方偏移量(MSD)算法。定义
MSD(n)=E[‖z(n)‖2],
(22)
基于(15)式,可得
‖z(n+1)‖2=zT(n+1)z(n+1)=
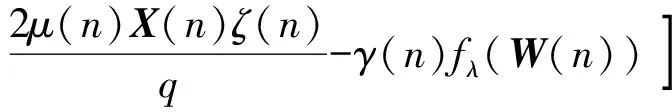
(23)
对(23)式等号两端取期望,化简可得
E[zT(n)fλ(W(n))]+λ2E[μ2(n)]·
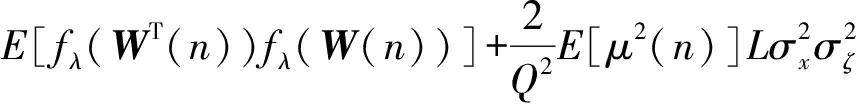
(24)

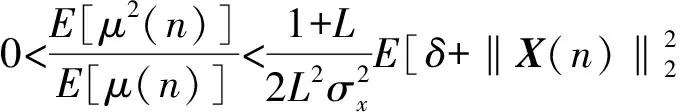
(25)
当n→∞时,得
fλ(W(∞))=
(26)
此时(24)式表示为
MSD(∞)=
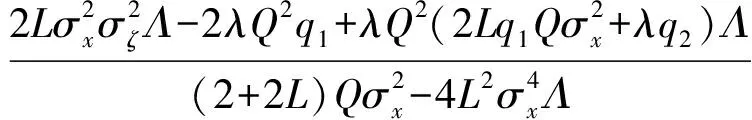
(27)
式中:
(28)
结合(8)式、(26)式、(27)式和(28)式,可得提出算法的MSD(∞)。
1.2.3 稳态MSE
在本节中,将给出本文所提算法稳态时的MSE. 结合(1)式和(2)式,得
e(n)=ζ(n)-XT(n)z(n).
(29)
定义MSE表示为MSE(n)=E[e2(n)],则
MSE(n)=E[ζ2(n)]+E[zT(n)X(n)XT(n)z(n)]=
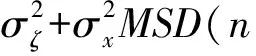
(30)
结合(8)式和(30)式,可得到所提出算法的稳态MSE:
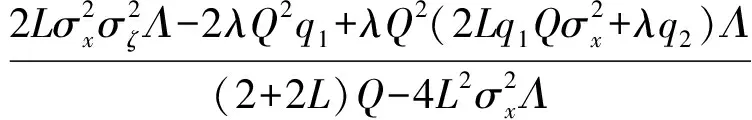
(31)
求解(28)式和(31)式,需要求解Λ=E[μ2(∞)]/E[μ(∞)]. 由(10)式得
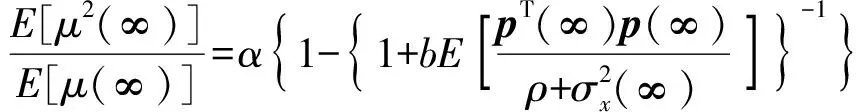
(32)
由(12)式得
E[pT(n)p(n)]=χ2E[pT(0)p(0)]+
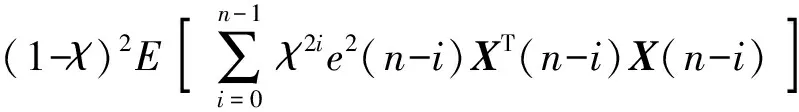
(33)
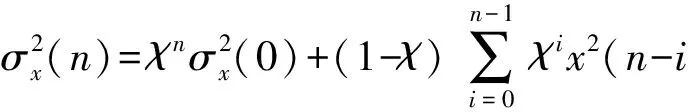
(34)
结合(32)式~(34)式,可得
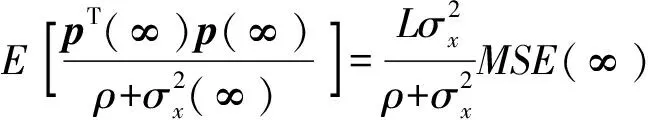
(35)
把(35)式代入(32)式即可得Λ.
2 算法性能仿真分析
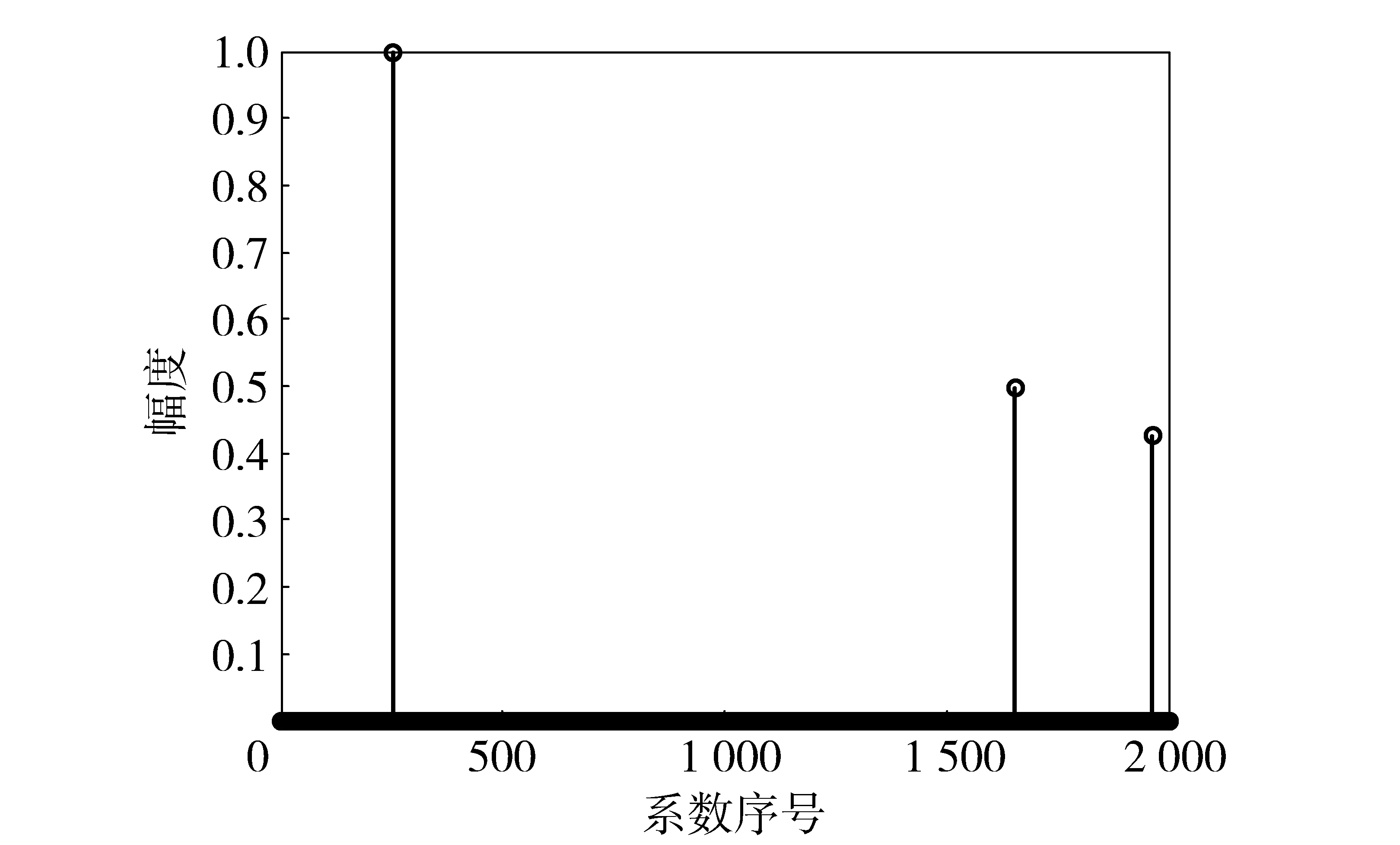
图1 稀疏系统的脉冲响应Fig.1 Impulse response of sparse system
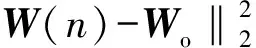
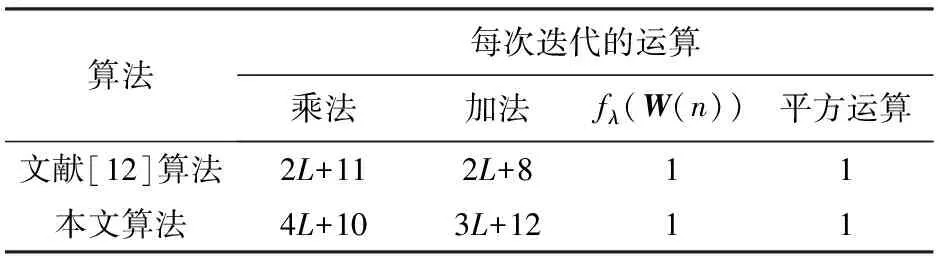
表1 算法复杂度比较
从表1可知,本文提出算法计算复杂度有所提高,是因为提出的算法中需要估计输入信号的方差以及系统参数迭代运算中的归一化运算。
实验1 此实验中各参数的设置见表2,仿真结果见图2. 系统输入不相关信号,且SNR=20 dB. 图2(a)和图2(b)分别表示μ和MSD的比较曲线。
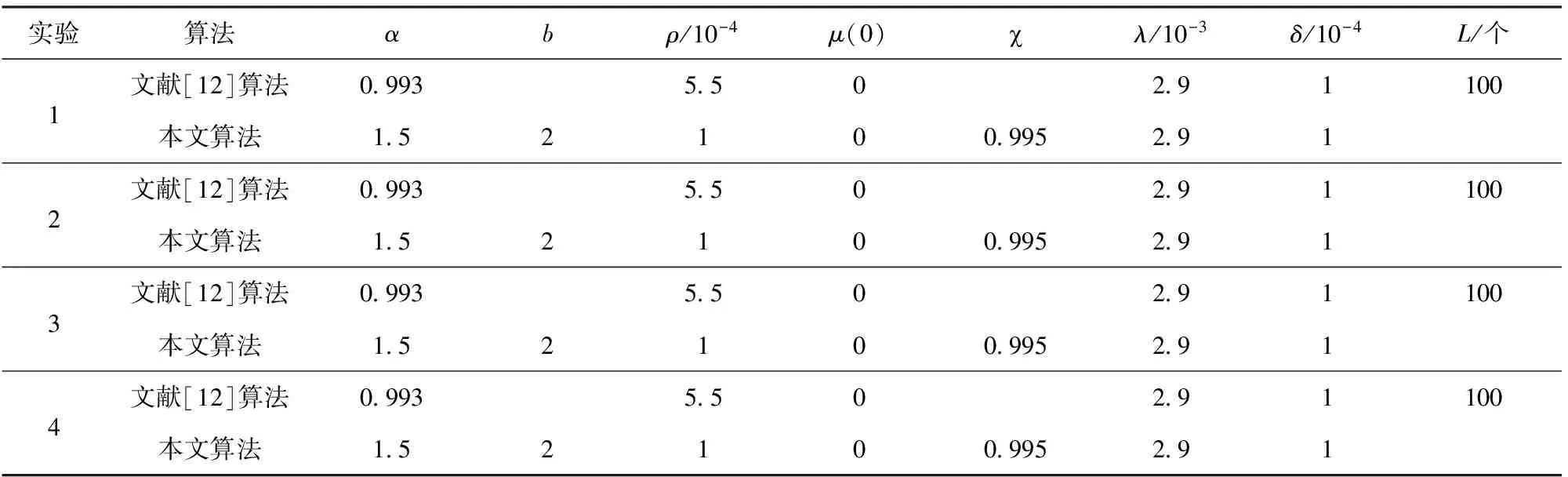
表2 实验中各参数的设定
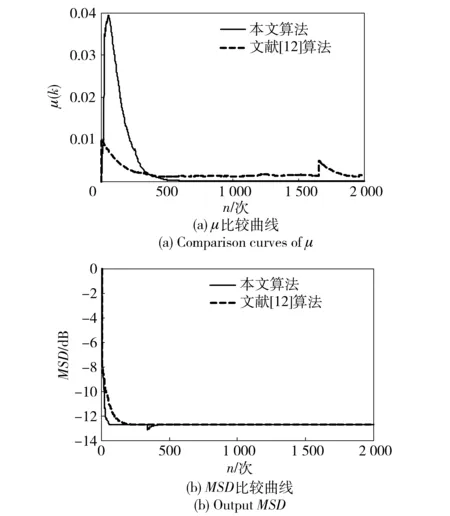
图2 μ和MSD的各自比较曲线Fig.2 Output MSD and comparison curves of μ
实验2 此实验中各参数的设置见表2,仿真结果见图3. 系统输入不相关信号,且SNR=3 dB. 图3(a)和图3(b)分别表示μ和MSD的比较曲线。
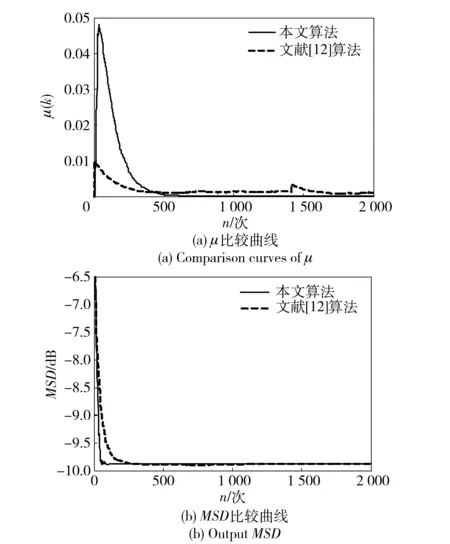
图3 μ和MSD的各自比较曲线Fig.3 Output MSD and comparison curves of μ
实验3 此实验中各参数的设置见表2,仿真结果见图4. 系统输入相关系数为0.5的相关信号,且SNR=20 dB. 图4(a)和图4(b)分别表示μ和MSD的比较曲线。
实验4 此实验中各参数的设置见表2,仿真结果见图5. 系统输入相关系数为0.5的相关信号,且SNR=3 dB. 图5(a)和图5(b)分别表示μ和MSD的比较曲线。
从实验结果图2与图4的比较或是图3与图5的相比可知:当处于相同信噪比时,输入相关信号或不相关信号,相比文献[12]提出的算法,本文提出的算法在收敛初期步长较大,具有较快的收敛速度;在稳态时步长值较小,因此有低稳态误差。
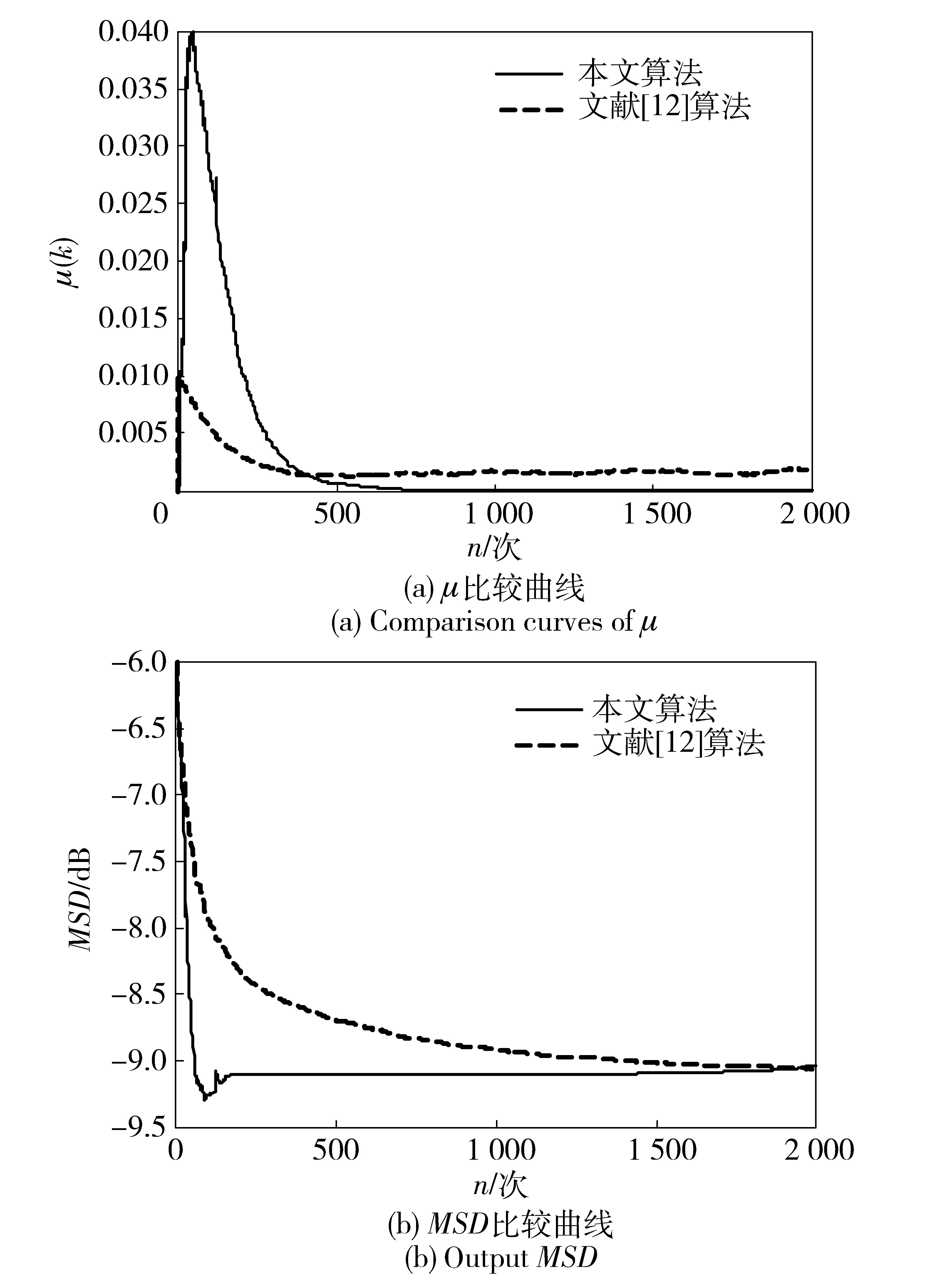
图4 μ和MSD的各自比较曲线Fig.4 Output MSD and comparison curves of μ
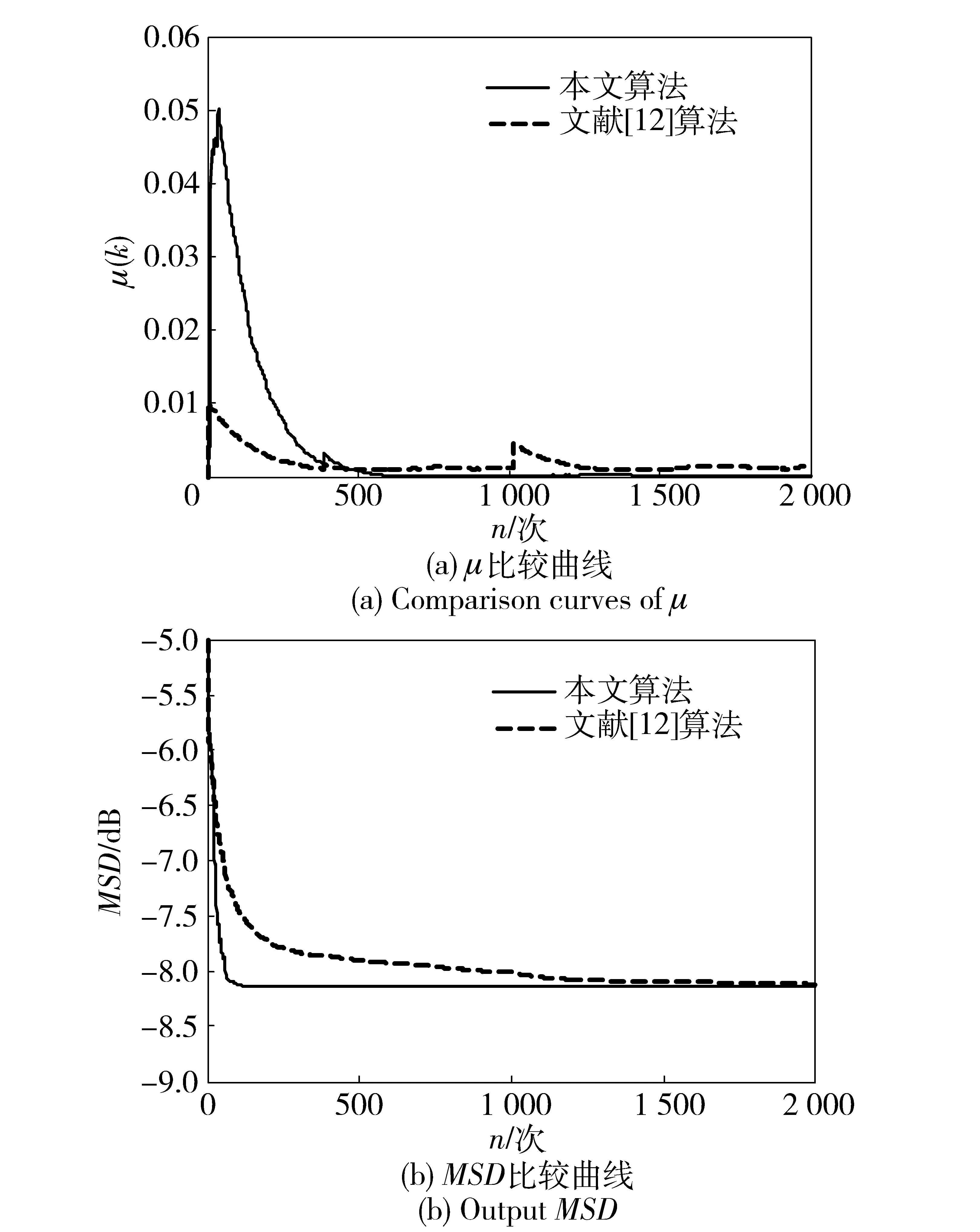
图5 μ和MSD的各自比较曲线Fig.5 Output MSD and comparison curves of μ
从实验结果图2与图3的比较或是图4与图5的相比可知:当输入相关信号或不相关信号时,不论是高SNR还是低SNR,相比文献[12]提出的算法,本文提出的算法在收敛初期步长较大,具有较快的收敛速度;在稳态时步长值较小,因此有低稳态误差。
总之,不论输入信号相关与否还是信噪比的高低,本文提出的算法收敛速度较快,稳态性能好,进而能有效地识别稀疏系统。
3 结论
为能降低在l0-NLMS算法中系统的噪声影响,并提高其收敛速度,且降低输入信号的影响,本文给出一种带零吸收项的l0-NLMS算法。相比文献[12]提出的算法,本文所提出的算法具有良好的抗噪声性能。此外,应用于识别稀疏系统的实验仿真结果表明:输入相关信号或不相关信号时,本文提出的算法都具有快的收敛速度和低的稳态误差;同时,此实验仿真结果也表明:当输入高信噪比或低信噪比的信号时,本文提出的算法同样保持好的收敛性能和好的稳态性能。总之,本文提出带零吸收项的l0-NLMS算法在收敛速度与抗系统噪声方面都具有良好的性能,且降低了输入信号的影响,在稀疏信道的识别方面具有很大的实用前景。
References)
[1] Diniz P S R. Adaptive filtering [M]. 4th ed. Boston, MA, US: Springer, 2013.
[2] Yoo J W, Shin J W, Park P G. An improved NLMS algorithm in sparse systems against noisy input signals[J]. IEEE Transactions on Circuits and Systems II-Express Briefs, 2015, 62(3):271-275.
[3] 伍飞云, 周跃海, 童峰, 等. 可适应稀疏度变化的非均匀范数约束水声信道估计算[J]. 兵工学报, 2014, 35(9):1503-1509. WU Fei-yun, ZHOU Yue-hai, TONG Feng, et al. Non-uniform norm constraint estimation algorithm for underwater acoustic channels at the presence of varying sparsity[J]. Acta Armamentarii, 2014, 35(9):1503-1509. (in Chinese)
[4] Nunoo S, Ngah R, Chude-Okonkwo U A K. Performance of LMS, NLMS and LMF algorithms in tracking time-varying UWB channels[C]∥IEEE International Conference on Signal and Image Processing Applications. Melaka: IEEE, 2013:312-316.
[5] Kwong R H. A variable step-size LMS algorithm[J]. IEEE Transactions on Signal Processing, 1992, 40(7):1633-1641.
[6] Aboulnasr T, Mayyas K. A robust variable step-size LMS type algorithm: analysis and simulations[J]. IEEE Transactions on Signal Processing, 1997, 45(3):631-639.
[7] Zhao S, Man Z, Khoo S, et al. Variable step-size LMS algorithm with a quotient form[J]. Signal Processing, 2009, 89(1):67-76.
[8] Li M, Li L P, Tai H M. Variable step size LMS algorithm based on function control[J]. Circuits Systems & Signal Processing, 2013, 32(6):3121-3130.
[9] Taheri O, Vorobyov S A. Reweightedl1-norm penalized LMS for sparse channel estimation and its analysis[J]. Signal Processing, 2014, 104(6):70-79.
[10] Gu Y T, Jin J, Mei S L.l0norm constraint LMS algorithm for sparse system identification[J]. IEEE Signal Processing Letters, 2009, 16(9): 774-777.
[11] Chen Y, Gu Y, Hero A O. Sparse LMS for system identification[C]∥IEEE International Conference on Acoustics, Speech, & Signal Processing. Taipei: IEEE, 2009:3125-3128.
[12] Turan C, Salman M S. Zero-attracting function controlled VSSLMS algorithm with analysis[J]. Circuits Systems and Signal Processing, 2015, 34(9): 3071-3080.
[13] Yu Y, Zhao H. An improved variable step-size NLMS algorithm based on a versiera function[C]∥IEEE International Conference on Signal Processing, Communication and Computing. Kunming, China: IEEE, 2013.
[14] Huang H, Lee J. A new variable step-size NLMS algorithm and its performance analysis [J]. IEEE Transactions on Signal Processing, 2012, 60(4):2055-2060.
[15] 徐洋, 徐松涛, 马健, 等. 基于Sigmoid二次型隶属度函数的改进LMS算法[J]. 中南大学学报:自然科学版, 2014, 45(10):3470-3476. XU Yang, XU Song-tao, MA Jian, et al. Improved LMS algorithm based on Sigmoid quadratic membership function[J]. Journal of Central South University: Science and Technology, 2014, 45(10):3470-3476.(in Chinese)
[16] Wang Y L, Tian X L. A modified speech enhancement algorithm for electronic cochlear implant and its digital signal processing realization[J]. Journal of Biomedical Engineering, 2014, 31(4):742-746,754.
[17] 曲庆, 金坚, 谷源涛. 用于稀疏系统辨识的改进l0_LMS算法[J]. 电子与信息学报, 2011, 33(3):604-609. QU Qing, JIN Jian, GU Yuan-tao. An improvedl0-LMS algorithm for sparse system identification[J]. Journal of Electronics and Information Technology, 2011, 33(3):604-609.(in Chinese)
[18] 管四海, 李智. 改进的l0范数LMS算法与分析[J]. 北京邮电大学学报, 2015, 38(4):81-85. GUAN Si-hai, LI Zhi. A modifiedl0_LMS algorithm and its performance analysis[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(4):81-85.(in Chinese)
[19] 万涛, 刘遵雄, 王树成. 用于稀疏系统辨识的改进惩罚LMS算法研究[J]. 华东交通大学学报, 2013, 30(6):62-66. WAN Tao, LIU Zun-xiong, WANG Shu-cheng. The improvement of LMS algorithm for sparse system identification[J]. Journal of East China Jiaotong University, 2013, 30(6):62-66.(in Chinese)
[20] 伍飞云, 周跃海, 童峰. 引入梯度导引似p范数约束的稀疏信道估计算法[J]. 通信学报, 2014, 35(7):172-177. WU Fei-yun, ZHOU Yue-hai, TONG Feng. Estimation algorithm for sparse channels with gradient guidedp-norm like constraints[J]. Journal on Communications, 2014, 35(7):172-177.(in Chinese)
[21] Benesty J, Rey H, Vega L R, et al. A nonparametric VSS NLMS algorithm[J]. IEEE Signal Processing Letters, 2006, 13(10):581-584.
Modified Zero-Attractingl0-NLMS Algorithm
GUAN Si-hai1, LI Zhi1, HUANG Hui2, WANG Zhe3
(1.School of Mechano-Electronic Engineering, Xidian University, Xi’an 710071, Shaanxi, China; 2.School of Electronic Engineering, Xidian University, Xi’an 710071, Shaanxi, China; 3.Xi’an Aerospace Power Measurement and Control Technology Institute, Xi’an 710025, Shaanxi, China)
A new zero-attracting variable step sizel0-NLMS algorithm is proposed for recognition of sparse system. Step size ofl0-NLMS algorithm is changed by the versiera function. The convergence and convergence conditions, and the mean square error (MSE) and mean square deviation (MSD) of the proposed algorithm are derived. Simulation experiments with different signal-to-noise ratios (SNR) and different levels of autocorrelation of input signal are performed to compare the step size and MSD. The experimental simulation results show that the proposed algorithm can achieve faster convergence rate and good performance of pattern recognition even when the input signal is correlated, and can identify the sparse systems effectively.
information processing technology; sparse system;l0-NLMS algorithm; variable step size; system noise; versiera function
2016-01-06
国家自然科学基金项目(61074120);高等学校博士学科点专项科研基金项目(2011020311004)
管四海(1990—),男,博士研究生。E-mail:gcihey@sina.cn; 李智 (1961—),男,教授,博士生导师。E-mail:zhli@xidian.edu.cn
TN911.72
A
1000-1093(2016)11-2170-07
10.3969/j.issn.1000-1093.2016.11.027

