综合优先级规划下的相控阵雷达自适应调度方法

张浩为， 谢军伟， 盛川

(空军工程大学 防空反导学院， 陕西 西安 710051)



综合优先级规划下的相控阵雷达自适应调度方法

张浩为， 谢军伟， 盛川

(空军工程大学 防空反导学院， 陕西 西安 710051)

对时间资源的合理分配是相控阵雷达发挥自身优势的关键，提出一种考虑目标威胁度的相控阵雷达调度算法。根据目标信息构建非线性目标威胁度量化模型，并通过设计二维优先级表，将目标威胁度与雷达任务的截止期相结合，共同进行综合优先级规划；在性能评估环节，提出执行威胁率的概念，以反映调度算法对重要任务的执行情况。仿真结果表明，当跟踪目标数量饱和时，相比于原有的高工作方式优先级优先算法，改进后的算法有效减少了任务的截止期错失率，提升了时间利用率和执行威胁率。

兵器科学与技术； 相控阵雷达； 自适应调度； 综合优先级； 目标威胁度

0 引言

相控阵雷达具有良好的波束捷变和波形自适应能力，可以同时完成搜索和跟踪等多种任务，相较于传统机械扫描雷达而言优势明显。这种优势的发挥正是基于相控阵雷达对时间资源的合理分配：利用时间分割原理，对各个时间段分配特定的任务，以达到对硬件资源综合、高效利用的目的。因此，研究如何在时间资源有限[1]的约束下，实现任务的最优分配，对发挥相控阵雷达的自身优势有着重要意义。

相控阵雷达调度模块决定着任务分配，可分为两大部分：任务优先级规划和调度策略的选择。传统的优先级规划算法中，事先根据不同种类的任务赋予其不同的优先级，并且在调度过程中固定不变，自适应能力差。随着截止期最早最优先算法[2-3](EDF)的引入，雷达性能得到提高。现今的任务优先级规划中，常常考虑任务的多种属性，得到综合优先级序列。文献[4-5]提出了工作方式优先级加截止期(HPEDF)的调度算法：将任务的截止期和工作方式两种因素映射到同一层面，以计算任务综合优先级。文献[6-7]仿真证明了HPEDF算法调度性能优于着重考虑单一因素的算法。文献[8]借鉴HPEDF算法的思想，综合可用资源等多种因素进行调度，取得了较好效果。文献[9-11]利用了目标的单属性因素来划分雷达任务的综合优先级，但线性加权网络难以反映多种目标属性对雷达威胁的非线性变化。相控阵雷达的调度策略可分为模板法和自适应方法。其中，自适应方法能够最大程度上发挥相控阵雷达的综合优势。文献[12-13]提出并研究了在自适应调度中加入时间窗的方法，可将波束驻留的实际执行时刻在期望执行时刻的时间窗范围内前后移动，提高了任务调度的成功率。文献[14-17]利用脉冲交错技术，进一步提升了雷达对时间资源的利用率。文献[18-19]提出了基于收益的调度算法，通过构建收益函数及约束条件，运用启发式方法进行求解。但上述算法均存在有以下缺陷：一是未充分利用目标的先验信息；二是雷达任务仍属于人为划分工作方式优先级的范畴，由此来评定实现价值率的高低，受主观因素的影响较大。

为此，提出一种基于综合优先级的相控阵雷达自适应调度方法。充分利用目标信息建立非线性的目标威胁度模型，将目标威胁度与雷达任务的优先等级相联系，以避免人为划分的影响；通过设计二维动态优先级表，综合目标威胁度与任务截止期共同确定任务的优先等级；提出执行威胁率的概念，替换已往实现价值率的指标，以反映调度算法对重要任务的执行情况；进行仿真实验，证明本文算法的有效性。

1 目标威胁模型

影响目标威胁度的因素众多，现主要考虑以下几点：目标类型威胁，目标的运动属性威胁，即目标与雷达距离、目标速度、目标航向和目标高度威胁。由于多个目标属性因素对雷达的威胁是非线性的，对目标威胁度进行如下量化计算：

1) 定义目标径向距离威胁函数：

(1)

式中：R为目标与雷达的径向距离；Rgmax为雷达制导导弹杀伤远界；Rdmax为雷达最远探测距离；s为常系数。其中，s值越小，威胁函数曲线随距离的增大下降得越为缓慢。考虑到目标处于雷达最远探测距离之外时，威胁较小，一般取s≥0.5. (1)式表明，目标距雷达越近，威胁度越大，在临近导弹杀伤远界时，威胁度迅速增大。

2) 考虑目标低速时威胁较小，当速度超出一定值时，威胁迅速上升，定义“S”形速度威胁函数：

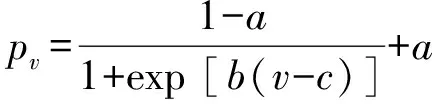
(2)

式中：v为目标速度值；a表示目标速度低于雷达跟踪下限时的威胁大小，可由专家确定；b为控制函数曲率的常系数，当取b>1时，速度威胁函数曲线基本呈阶梯状分布；c为控制曲线两个拐点的常系数。其中，c值越大，曲线拐点对应的速度值越大。

3) 定义目标指向雷达水平方向失量与目标速度失量之间的夹角为目标航向角θ. 当θ=0°时，目标径直飞向我方，对雷达威胁最大；当θ=180°时，目标径直飞离我方，威胁度最小。则目标角度威胁函数[20]为

pθ=exp (-dθ)，

(3)

式中：d为控制航向威胁函数的常系数。其中，d值越大，函数拐点对应θ值越小，曲线下降越剧烈。当d≥0.05时，曲线基本呈“L”形分布，故一般取d(0,0.05)；θ[0°,180°]。

4) 考虑目标低空突防的威胁，定义高度威胁函数[21]为

(4)

式中：h为目标高度；e为常系数，其值越大，函数减小越快，一般取e[0.01,0.05]；H为临界高度，可由专家确定。

5) 目标类型[22]中，考虑以下5种典型情况：战术导弹、战斗机、轰炸机、直升机和干扰机，定义目标类型威胁值为pT，可由专家确定。

基于上述函数，构造目标威胁度函数：

pt=pT(λ1pR+λ2pv+λ3pθ+λ4ph)，

(5)

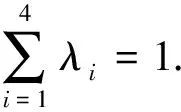
2 雷达任务建模

典型的相控阵雷达任务可分为4类：确认、跟踪、失跟处理和搜索。任务的请求顺序一般为：搜索—确认—跟踪(—失跟处理—跟踪维持)。跟踪任务可具体分为精密跟踪、普通跟踪和监视3种。当确认目标存在后，雷达将依据目标的威胁程度划分跟踪方式：目标威胁度由高到低依次对应精密跟踪、普通跟踪和监视任务。第j个任务模型可表示为

Tj={Pj,taj,tdwj,twj,tdj,Δtj,Numj,Inj}，

(6)

式中：Pj为任务的工作方式；taj为任务的请求执行时刻；tdwj为任务驻留时间；twj为时间窗；tdj为任务截止期；Δtj为任务间的采样间隔；Numj为任务执行次数；Inj为目标信息。各驻留任务间的请求执行时刻可表示为

taj=te(j-1)+Δtj，

(7)

式中：te(j-1)为上一次任务成功执行时刻。任务的截止期可表示为

tdj=taj+twj.

(8)

目标信息In可详细表示为

In={TY,R,v,θ,h,pt}，

(9)

式中：TY代表目标类型。(9)式中变量均满足(5)式。

3 改进算法描述

3.1 综合优先级规划

任务调度的基本原则如下：1) 重要性原则，即重要的任务优先调度；2) 紧急性原则，即紧急的任务优先调度[18]。在此，将目标威胁度视做任务价值，通过设计二维动态优先级表，将目标威胁度与任务截止期映射到同一层面：即在一个调度间隔内，将所有请求任务分别按照目标威胁度ptj由大到小和截止期dj由小到大进行排序，记第j个任务在两个序列中的位置分别为m、n，构建综合优先级函数：

pj=[f×(m-1-g)+2×n-2]×(m+g)/2+m，

(10)

式中：f为倾向目标威胁度的加权系数；g为(n-2)/f向0取整。其中，pj值越小，任务优先等级越高。为设计简单，一般取f为1～5. 图1(a)和图1(b)分别给出了f=1与f=2时的优先级表设计方案。当取f→∞时，任务的综合优先级主要由目标威胁度确定。当目标威胁度相同时，截止期越小，任务的优先等级越高。

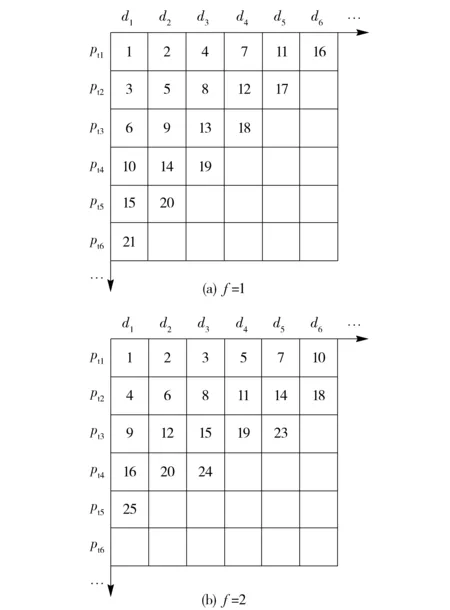
图1 优先级表设计Fig.1 Design of priority table

通过动态二维优先级表，可以将雷达任务中包含的目标威胁度与任务本身的截止期相结合，来确定任务的优先等级。这不仅消除了两者量纲上的差异，而且保证了每一个任务对应优先级的唯一性[23]。

3.2 调度策略

为对时间资源进行充分利用，借鉴时间指针调度算法[4]的思想，在一个调度间隔内，按综合优先级大小依次安排请求任务，具体步骤如下：

1) 获取该调度间隔的初始参数：申请队列长度Nr、时间指针tP和调度间隔结束时间te，令i=0；

2) 设申请任务队列中共有M个截止期小于tP的任务，将它们删除，则i=i+M；

3) 从申请任务队列中取出最早可执行时间小于等于tP的任务，按照(10)式计算它们的综合优先级，选出具有最大优先级的任务T；

4) 若剩余时间满足任务执行条件，将任务T送入执行链表，更新参数tP=tP+tdw，并将任务T从申请队列中删除，令i=i+1；反之，送入延时任务队列，转步骤6；

5) 当tP≥te或i≥Nr时，转到步骤6；反之，转到步骤2；

6) 遍历剩余请求任务，若满足延时任务条件，则送入延时任务队列，更新参数taj=te，twj=twj-(te-taj)；反之，送入删除队列；

7) 调度间隔结束，得到执行链表、延时任务链表、删除链表和参数tP.

调度流程如图2所示。

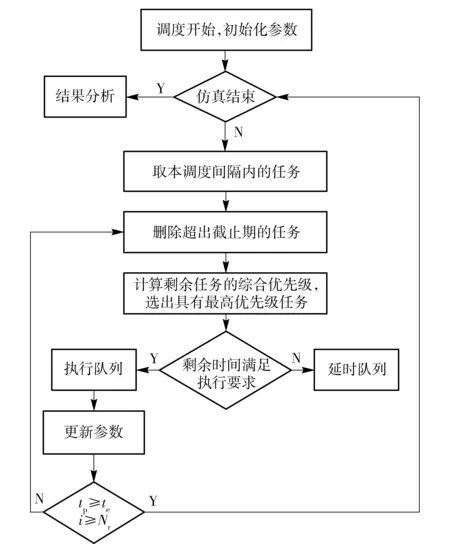
图2 调度算法流程Fig.2 Flow chart of scheduling algorithm

4 评估指标

评判调度算法的性能优劣，需要以下指标：

1) 调度成功率[6](SSR)：即成功调度的任务数量与请求调度的任务数量之比，如(11)式所示：

SSR=Ns/Ntot，

(11)

式中：Ns为成功调度的任务总数；Ntot为请求调度的任务总数。

2) 截止期错失率 (DMR)：未成功调度的任务数量与请求调度的任务数量的比值[6]，常用作反映调度算法对各类任务的调度性能。第j类任务的DMR可表示为

DMRj=Nlj/Ntotj，

(12)

式中：Nlj为第j类任务的丢失数量；Ntotj为第j类任务的请求总数。

3) 时间利用率(TUR)：即成功执行的所有任务所用时间与可用时间的比值，可表示为

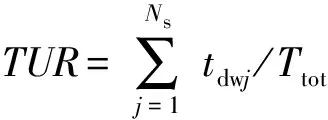
(13)

式中：Ttot为总的可用时间。在调度过程中，算法应充分利用时间资源对任务进行调度，因此，时间利用率越高，算法性能越佳。

4) 由于任务的重要性是随目标威胁程度而变化的，并不依赖于人为划分，因此，本文引入执行威胁率(TRE)的概念，代替原有的实现价值率[6]，用以反映调度算法对重要任务的调度性能。执行威胁率即为调度成功的任务所具有的目标威胁度总和与请求任务目标威胁度总和之比，公式为

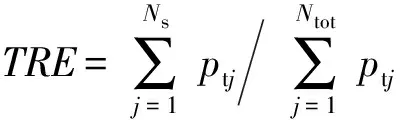
(14)

从(14)式可以看出，调度过程中，应优先考虑对具有高威胁度目标属性的任务进行调度，因此，执行威胁率越高，算法的性能越佳。

5 仿真实验

5.1 参数设定

目标威胁模型中，取s=3；Rgmax=100 km；Rdmax=250 km；a=0.15；b=0.05；c=200；d=0.01；e=0.03；H=0.5 km. 运用层次分析法确定目标威胁度模型中的各个权重值。仿真中，对比本文算法和传统算法：HPEDF 算法[5]和高工作方式优先级优先 (HPF) 算法[3]。调度间隔(SI)取50 ms，参数设置[19]如表1所示。

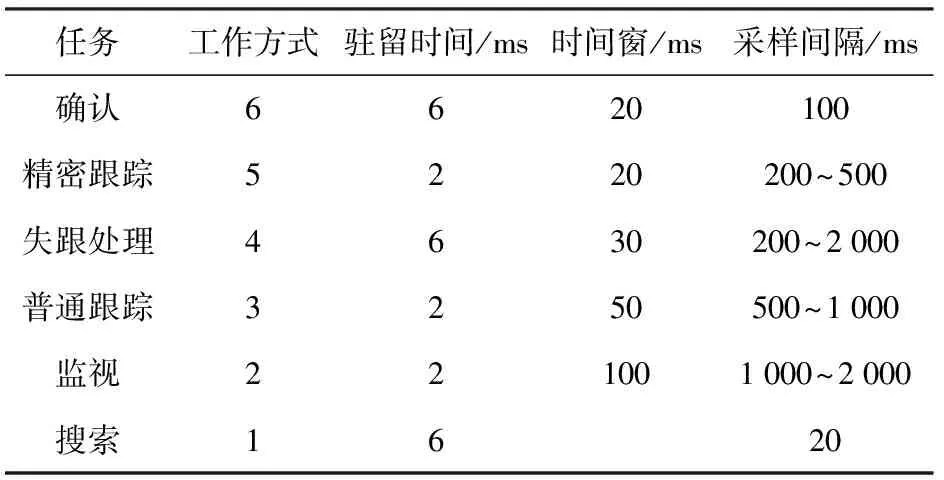
表1 任务参数表

仿真中，由场景发生器在雷达搜索扇区内产生第1节所考虑的5种随机目标，当目标进入雷达探测范围后，以一定概率被搜索到。目标的各类参数随机产生，且均匀速向雷达运动。雷达采用跟踪加搜索的工作方式，当对某批目标的跟踪次数小或等于2次时，若跟踪任务被删除，则不产生失跟处理请求；当雷达对某目标的稳定跟踪任务(跟踪次数大于3次)数据率达不到要求时，则产生失跟处理请求。仿真时长为50 s (1 000个调度间隔)，雷达跟踪目标数0～80批，精密跟踪、普通跟踪和监视目标数之比为2∶3∶5，每增加10批进行100次仿真实验，结果取平均值，统计如图3所示。

5.2 结果分析

图3(a)为3种算法的调度成功率对比，图3(b)、图3(c)分别为3种算法的跟踪任务截止期错失率对比和搜索任务截止期错失率对比。从图3(a)～图3(c)中可以看出，HPF算法在目标数量达到40批时已经开始丢失搜索任务，导致调度成功率降低；而本文算法和HPEDF算法在目标数量达到50批时才开始丢失搜索任务，导致调度成功率下降。在传统算法中，任务的重要性均由人为划分，并且在调度过程中固定不变，因此传统算法中任务的综合优先级的变化主要由任务的截止期决定；而本文算法通过目标威胁模型和动态优先级表，将任务的重要性和紧迫性同时置于动态优先级中，因此，可以调度更加重要和紧急的任务。当目标数量超过50批时，相比于传统算法，本文算法的跟踪任务截止期错失率和搜索任务截止期错失率上升得更为缓慢。

图3(d)为3种算法的时间利用率对比，从中可以看出，HPF算法对时间的利用率最低；当雷达跟踪目标数目达到饱和时，本文算法和HPEDF算法均对时间资源进行了充分利用。图3(e)为3种算法的执行威胁率对比，结合图3(b)、图3(c)可以看出，在传统算法中，搜索任务被固定于最低优先级，过载情况下将被最先删除，因而搜索任务截止期错失率呈直线上升趋势 (在跟踪80批目标时，传统算法的搜索任务截止期错失率均达到1)；而本文算法中，搜索任务具有动态优先级，甚至可以抢占跟踪任务，因此，搜索任务截止期错失率呈缓慢上升趋势，维持了较好地搜索和发现性能。在跟踪目标数量饱和的情况下，进一步增加跟踪目标数量，将导致失跟处理任务迅速增加。传统算法将失跟处理任务固定于第4工作方式优先级，使得其大部分被成功调度。但失跟处理任务的成功调度将使得搜索任务的截止期错失率进一步加剧。而本文算法中，任务的重要性由目标的威胁度来判定，因此，在过载情况下，可以舍弃低威胁目标的失跟处理任务和确认任务，以 维持对高威胁目标的跟踪性能，从而取得了更高的执行威胁率。当目标数目达到饱和时，相比于HPF算法，本文算法的跟踪任务截止期错失率减少了33%，搜索任务截止期错失率减少了44%，执行威胁率提升了45%.

图3 调度性能对比Fig.3 Comparison of performance indexes

改变目标威胁模型中的常系数，进一步进行仿真实验，发现3种算法在性能评估指标间的差异与图3基本一致。由于目标威胁模型只是用来区分目标威胁程度，以作为雷达划分精密跟踪、普通跟踪或监视任务的依据，与调度算法本身并无太大关系，所以改变目标威胁模型中的常系数后，对调度成功率无影响，而对于性能评估指标中的执行威胁率产生一定影响。这也证明了仿真结果的可靠性。

6 结论

针对相控阵雷达中时间资源的分配问题，利用目标信息构建了目标威胁度模型。通过设计优先级表，构建了基于目标威胁度和任务截止期的综合优先级函数。在此基础上，给出了新算法的详细流程。通过与已有算法进行对比，验证了改进算法的有效性。结果表明，相比于传统算法，改进算法有效降低了搜索和跟踪任务的截止期错失率，提升了时间利用率和执行威胁率。

随着计算机技术和微波天线技术的发展，计算机资源和能量资源对相控阵雷达性能发挥的制约将逐渐弱化，因此文章在考虑资源管理时，仅考虑了最主要因素——时间资源的约束及分配，未对能量和计算机资源过多加以考虑。

References)

[1] Zhang B Y, Li S H, Yan W, et al. An efficient scheduling method for phased array radars with limited time resources[C]∥Proceedings of the IET International Radar Conference. Guilin: IET, 2009: 1-4.

[2] Liu C L, Layland J.W. Scheduling algorithms for multiprogramming in a hard real-time environment[J]. Journal of the ACM, 1973, 20(1): 46-61.

[3] Miranda S L C, Baker C J, Woodbridge K, et al. Comparison of scheduling algorithms for multifunction radar[J]. IET Radar Sonar & Navigation, 2007, 1(6):414-424.

[4] 卢建斌, 胡卫东, 郁文贤. 多功能相控阵雷达实时任务调度研究[J]. 电子学报, 2006, 34(4): 732-736. LU Jian-bin, HU Wei-dong, YU Wen-xian. Research on real-time scheduling algorithm for multifunction phased array radar[J]. Acta Electronica Sinica, 2006, 34(4): 732-736. (in Chinese)

[5] Lu J B, Xiao H, Xi Z M, et al. Multifunction phased array radar resource management: real-time scheduling algorithm[J]. Journal of Computational Information Systems, 2011, 7(2):385-393.

[6] Lu J B, Xiao H, Xi Z M, et al. Phased array radar resource management: task scheduling and performance evaluation[J]. Journal of Computational Information Systems, 2013, 9(3): 1131-1138.

[7] 卢建斌. 相控阵雷达资源优化管理的理论与方法[D]. 长沙:国防科学技术大学, 2007. LU Jian-bin. Theory and method resource optimization and management for phased array radars[D]. Changsha: National University of Defense Technology, 2007. (in Chinese)

[8] 郑世友, 郑瑶. 基于任务综合规划的相控阵自适应调度方法[J]. 计算机仿真, 2013, 30(7): 11-16. ZHENG Shi-you, ZHENG Yao. Adaptive task scheduling algorithm based on synthesizing programming for phased array radar[J]. Computer Simulation, 2013, 30(7):11-16. (in Chinese)

[9] 卢建斌, 胡卫东, 郁文贤. 多功能相控阵雷达实时驻留的自适应调度算法[J]. 系统工程与电子技术, 2005, 27(12): 1981-1984. LU Jian-bin, HU Wei-dong, YU Wen-xian. Adaptive scheduling algorithm for real-time dwells in multifunction phased array radars[J]. Systems Engineering and Electronics, 2005, 27(12): 1981-1984. (in Chinese)

[10] 赵宇, 李建勋, 曹兰英, 等. 基于二次规划的相控阵雷达任务自适应调度算法[J]. 系统工程与电子技术, 2012, 34(4): 698-703. ZHAO Yu, LI Jian-xun, CAO Lan-ying, et al. Adaptive scheduling algorithm based on quadratic programming for multifunction phased array radars[J]. Systems Engineering and Electronics, 2012, 34(4): 698-703. (in Chinese)

[11] 陈大伟. 相控阵雷达自适应调度算法研究[D]. 成都: 电子科技大学, 2011. CHEN Da-wei. The research on adaptive scheduling algorithm for phased array radar[D]. Chengdu: University of Electronic Science and Technology of China, 2011. (in Chinese)

[12] Huizing A G, Bloemen A F. An efficient scheduling algorithm for a multifunction radar[C]∥Proceedings of the IEEE International Symposium on Phased Array Systems and Technology. Boston, MA: IEEE, 1996: 359-364.

[13] Jang D S, Choi H L, Roh J E. A time-window-based task scheduling approach for multifunction phased array radars[C]∥Proceedings of the International Conference on control, Automation and Systems. Gyeonggi-do, Korea: IEEE, 2011: 1-6.

[14] Cheng T, He Z S, Li H Y. Adaptive dwell scheduling for digital array radar based on online pulse interleaving[J]. Chinese Journal of Electronics, 2009, 18(3):574-578.

[15] Cheng T, He Z S, Tang T. Novel radar dwell scheduling algorithm based on pulse interleaving[J]. Journal of Systems Engineering and Electronics, 2009, 20(2): 247-253.

[16] 唐婷, 何子述, 程婷. 一种基于模板法的自适应雷达驻留调度算法[J]. 信号处理, 2010, 26(7): 998-1002. TANG Ting, HE Zi-shu, CHENG Ting. A template-based adaptive radar dwell scheduling algorithm[J]. Signal Processing, 2010, 26(7): 998-1002. (in Chinese)

[17] Mir H, Guitouni A. Variable dwell time task scheduling for multifunction radar[J]. IEEE Transactions on Automation Science and Engineering, 2014, 11(2): 463-472.

[18] Cheng T, He Z S, Tang T. Dwell scheduling algorithm for multifunction phased array radars based on the scheduling gain[J]. Journal of Systems Engineering and Electronics, 2008, 19(3):479-485.

[19] Chen J, Tian Z, Wang L, et al. Adaptive simultaneous multi-beam dwell scheduling algorithm for multifunction phased array radars[J]. Journal of Information and Computational Science, 2011, 8(14): 3051-3061.

[20] 严世华, 刘华, 涂同飞. 一种红外多目标威胁度排序方法[J]. 火力与指挥控制, 2014, 39(6): 22-24. YAN Shi-hua, LIU Hua, TU Tong-fei. A threat sequencing method for aerial infrared muti-target[J]. Fire Control and Command Control, 2014, 39(6): 22-24. (in Chinese)

[21] 文飞, 吕艳, 段刚, 等. 空空威胁评估在综合辅助决策系统中的应用研究[J]. 系统仿真学报, 2009, 21(12), 3734-3737. WEN Fei, LYU Yan, DUAN Gang, et al. Application study of air-air threat assessment in synthetic decision aiding system[J]. Journal of System Simulation, 2009, 21(12): 3734-3737. (in Chinese)

[22] 史小斌, 顾红, 苏卫民, 等. 地面侦察雷达目标威胁度评估方法研究[J]. 兵工学报, 2015, 36(6): 1128-1135. SHI Xiao-bin, GU Hong, SU Wei-min, et al. Study of target threat assessment for ground surveillance radar[J]. Acta Armamentarii, 2015, 36(6): 1128-1135. (in Chinese)

[23] 王永炎, 王强, 王宏安, 等. 基于优先级表的实时调度算法及其实现[J]. 软件学报, 2004, 15(3): 360-370. WANG Yong-yan, WANG Qiang, WANG Hong-an, et al. A real-time scheduling algorithm based on priority table and its implementation[J]. Journal of Software, 2004, 15(3): 360-370. (in Chinese)

Adaptive Scheduling Algorithm over Comprehensive Priority for Phased Array Radar

ZHANG Hao-wei, XIE Jun-wei, SHENG Chuan

(Air and missile Defense College, Air Force Engineering University, Xi’an 710051, Shaanxi, China)

The high efficient time resource allocation in the phased array radar is the key to optimize its superiorities. A novel scheduling algorithm is proposed, which considers the threat level of targets. The nonlinear quantitative model of target threat level and the task deadline are mapped to the same layer to calculate the task comprehensive priority by designing the two-dimensional priority table. In the performance evaluation of the algorithm, the conception of executive threat rate is presented to reflect the execution of scheduling algorithm on the important tasks. The simulated results show that the proposed algorithm effectively decreases the deadline missing ratio of tasks, and improves the time utilization ratio and the executive threat rate compared with the previous high efficient priority algorithm in the saturated tracking task situation.

ordnance science and technology; phased array radar; adaptive scheduling; comprehensive priority; target threat level

2015-10-14

张浩为(1992—)，男，硕士研究生。E-mail:zhw_xhzf@163.com； 谢军伟(1970—)，男，教授，博士生导师。E-mail:xjw_xjw_123@163.com

TN954+.2

A

1000-1093(2016)11-2163-07

10.3969/j.issn.1000-1093.2016.11.026