基于改进型多目标粒子群优化算法的武器-目标分配
夏维, 刘新学, 范阳涛, 元锋刚
(1.火箭军工程大学 初级指挥学院, 陕西 西安 710025;2.91033部队, 山东 青岛 266034)
基于改进型多目标粒子群优化算法的武器-目标分配
夏维1, 刘新学1, 范阳涛1, 元锋刚2
(1.火箭军工程大学 初级指挥学院, 陕西 西安 710025;2.91033部队, 山东 青岛 266034)
在作战中武器- 目标分配(WTA)问题包含众多的变量,是典型的非确定性多项式完全问题。针对毁伤效能最大和用弹量最少两个目标函数,建立了基于改进型多目标粒子群优化(MOPSO-Ⅱ)算法的WTA模型。由于粒子群优化算法存在“维数灾难”瓶颈,应用了变量随机分解策略和合作协同进化框架,按照带精英策略的非支配排序遗传(NSGA-Ⅱ)算法中的排序方法对粒子群编码数据进行非支配排序。通过实例仿真分析,结果表明MOPSO-Ⅱ算法比NSGA-Ⅱ算法具有更好的求解精度与运行效率,能够获得满意的分配结果,且计算快速有效,比较适合较大规模的WTA问题实时求解。
兵器科学与技术; 多目标优化; 粒子群优化; 火力分配; Pareto集; 武器- 目标分配
0 引言
武器- 目标分配(WTA)问题,历来是作战指挥辅助决策研究中的核心内容之一,其解空间随着武器数目和目标总数的增加而呈指数级递增,是多参数、多约束的离散非确定性多项式(NP)完全问题[1]。WTA的核心思想是如何设计采用高效且健壮的算法,把具有不同杀伤力和价值成本的武器合理分配到不同的射击目标上,以构成整体优化的火力打击体系,使得作战效能最大。目前用于求解WTA问题的常用算法有遗传算法[2-3]、粒子群优化算法[4-9]、蚁群算法[10]、量子算法[11]、人工免疫算法[12]等,还有的采用算法的混合优化策略,如贪心算法与遗传算法结合[13]、禁忌搜索与微粒群优化结合[14]、蚁群算法与模拟退火算法结合[15-16]等。这些方法在提供了一种新思路的同时大都能够获得满意解,但都不同程度地存在着如下缺陷:易早熟、进化速度慢或者算法设计实现困难;绝大多数都针对的是某一时刻一种武器对应一批目标的作战背景,距离实战的标准要求甚远;算例中武器和目标的规模通常较小,面对规模较大、变量众多的WTA问题则比较束手无策。
本文在传统WTA问题追求最大作战效能的同时,新增“耗弹量最少”这一目标函数,将单目标优化问题转化为多目标优化,从而使得算法研究在未来作战中具有更加积极的现实意义。为解决传统多目标粒子群优化(MOPSO)算法中因“维数灾难”所导致的优化性能降低的问题,本文根据Potter等[17]提出的“分而治之”策略,提出一种新的改进型多目标粒子群优化(MOPSO-Ⅱ)算法,构造了有效表达武器- 目标分配的粒子编码、解码方案,并通过引入变量随机分解策略和合作协同框架,将大规模的变量问题分解到若干个维度适中的变量组——子种群当中,之后通过子种群之间的合作协同来实现对整个问题的求解,极大地提高了算法的求解效率,最后还通过仿真实例对比测试,验证了改进算法的快速性和精确性。
1 理论基础
1.1 WTA数学模型与数学性质
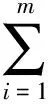

(1)
式中:xij表示第i类导弹对第j个目标分配的火力单元个数。第i类型号的每枚导弹对第j个目标的杀伤概率为eij,且0≤eij≤1,i=1,2,…,m,j=1,2,…,n,则杀伤概率矩阵为
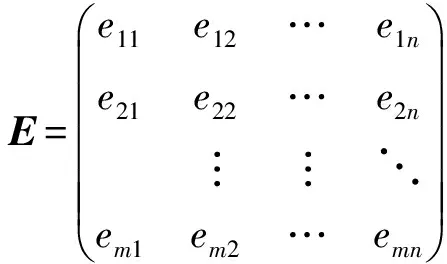
(2)
约束条件为:
1)第i类型号最多可以发射ci枚导弹,即
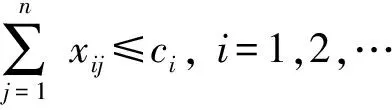
2)进攻方对目标Tj最多可使用sj枚导弹,即
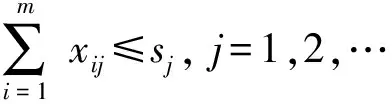
3)总分配导弹数目必须小于等于全部型号导弹所拥有的总数,即
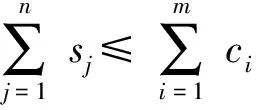
1.2 多目标优化与Pareto集
多目标优化问题的最优解通常称为Pareto最优解,如果用函数f来定义多目标优化问题,且函数把m维的决策变量X映射到n维的目标向量Y上,则该多目标优化问题的数学描述为
(3)
式中:X=(x1,x2,…,xm)由m个决策变量xi构成;Y由n个需要同时优化的目标函数fi(X)构成;约束条件g(X)由r个等式或不等式gi(X)≤0构成。则由多目标优化问题(3)式可引出如下定义:
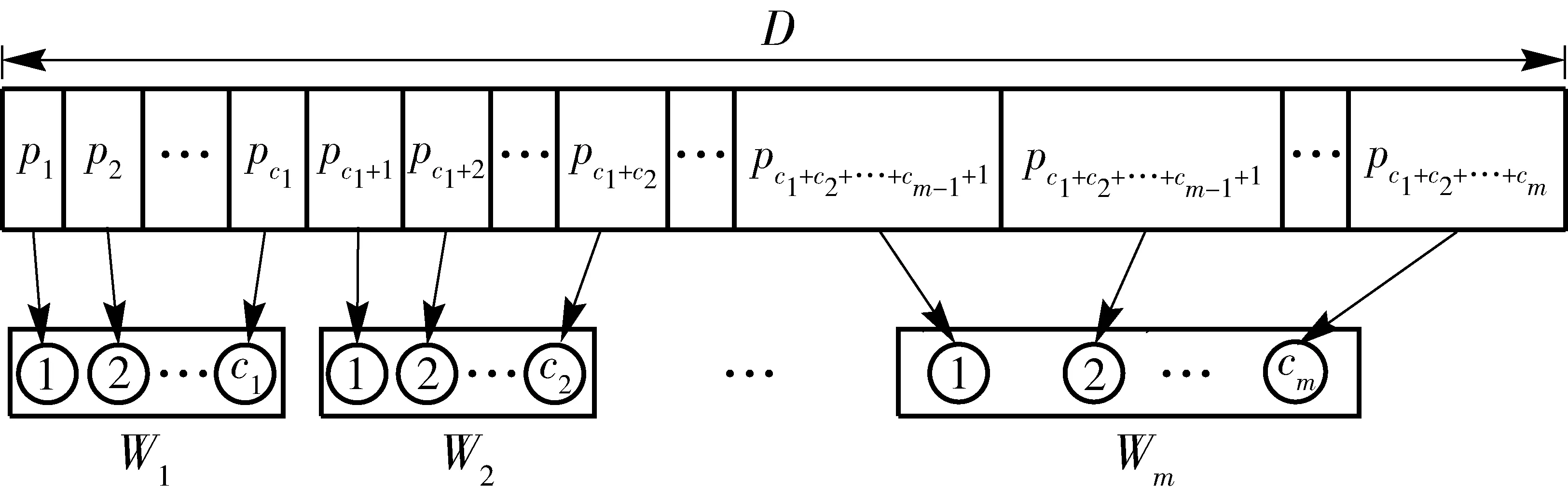
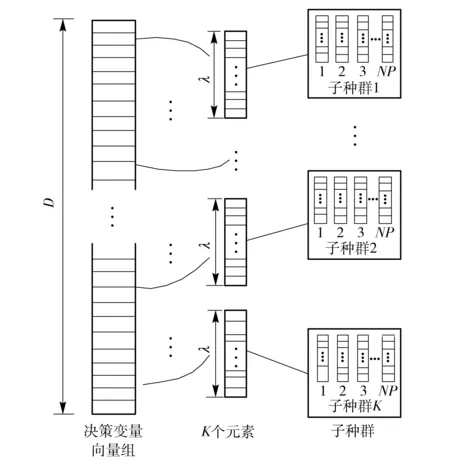
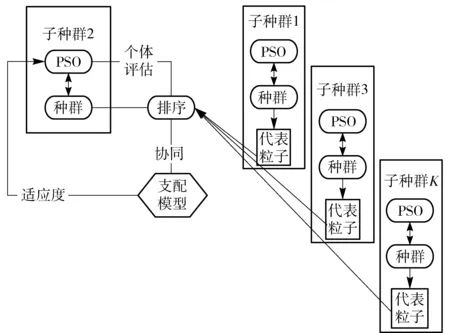
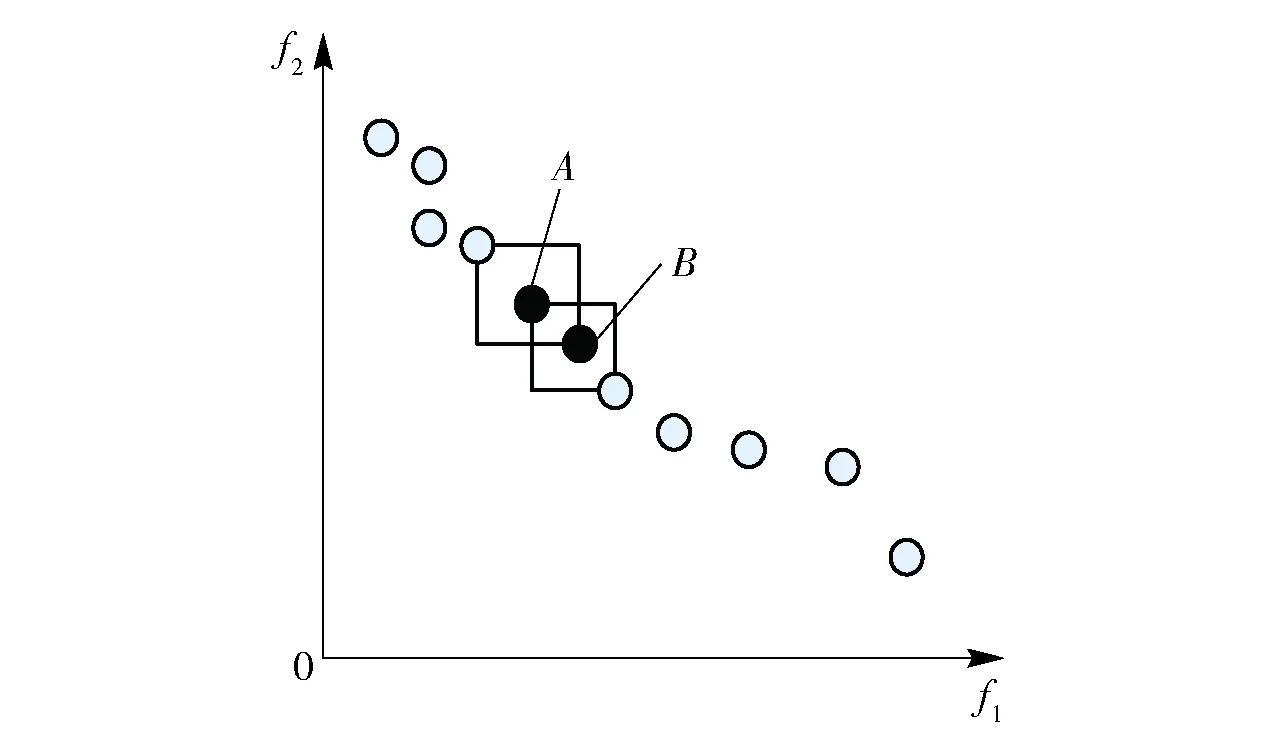
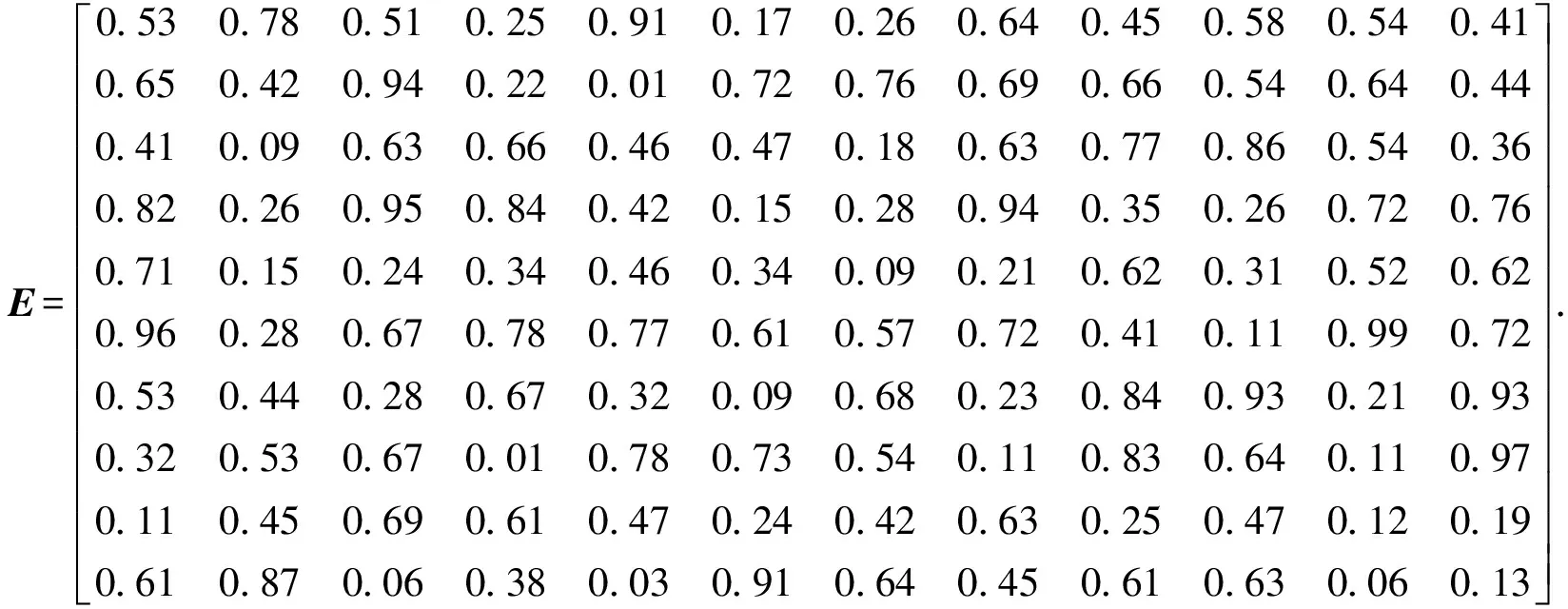
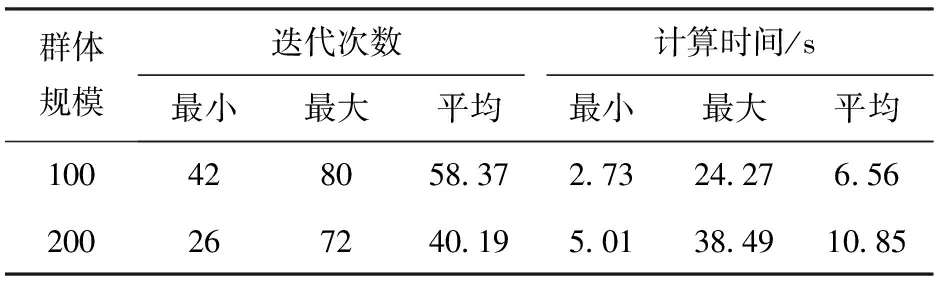
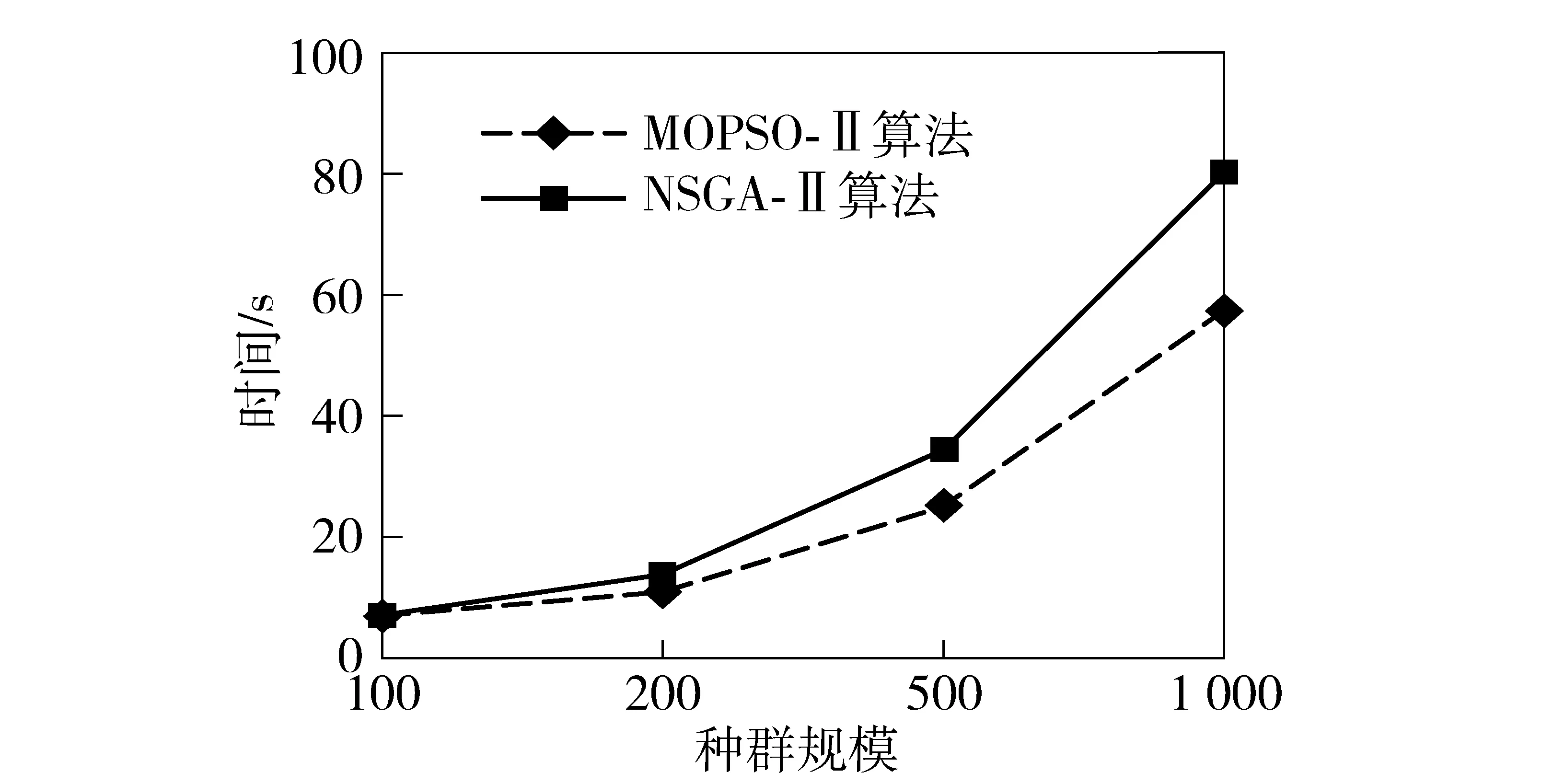
定义1 Pareto支配。设f:Rm→Rk,x1,x2∈Ω⊆Rm,称解x1支配解x2当且仅当f(x1)部分地优于f(x2),即∀i∈{1,2,…,k},fi(x1)≤fi(x2)∧∃i∈{1,2,…,k},fi(x1) 定义2 Pareto最优解。解x*∈Ω称之为解集合Ω的Pareto优化解当且仅当集合{x|x≼x*,x∈Ω}=∅. 定义3 Pareto最优解集,即所有Pareto最优解组成的集合。对于给定的多目标优化问题,设其定义域为Ω,则其Pareto最优集X*定义为:X*={x*|∃x∈Ω∶xx*}. 多目标WTA问题优化中,各目标之间往往互相冲突且计算困难,在规模较大的情况下,寻求使各目标同时达到最优的绝对最优解是不现实的,只能获得满意解,也即Pareto解,并且它不是唯一的。 1.3 多目标优化模型 WTA多目标优化模型具有毁伤效能指标最大和用弹量最少两个目标函数。 用一定数量的第i类型号导弹攻击第j个目标的杀伤概率可表示为 Pij=1-(1-eij)xij. (4) 则所有的m种型号导弹对目标j的毁伤概率Pj为 (5) (6) 为便于多目标计算,取目标函数f1=1-f最小来表示对敌毁伤期望f最大。 决策方案中,使用的导弹数目为 (7) 根据目标函数f1、f2和火力分配原则所构成的约束条件,建立WTA多目标规划数学模型为 (8) 1.4 MOPSO算法 粒子群优化(PSO)算法是由Kennedy等[20]于1995年提出的一种新型智能优化算法,源于对鸟群觅食行为中相互协作的研究,是一种大范畴群体智能算法。PSO算法利用粒子的个体认知和社会交互引导群体收敛到潜在的全局最优区域。假设D维解空间存在N个粒子,基本的PSO算法可表示为 vid(t+1)=ωvid(t)+C1r1(pid-xid(t))+ C2r2(pgd-xid(t)), (9) xid(t+1)=xid(t)+vid(t+1), (10) 式中:vid为粒子的速度向量;xid为当前粒子的位置;pid为粒子本身所找到的最优解pb;pgd为整个种群目前找到的最优解gb;r1与r2是介于[0,1]间的随机数;ω、C1和C2分别为控制这3部分内容的学习因子,ω又叫惯性权重,正常数C1和C2被称为加速因子。 1.5 合作协同进化框架 图1 合作协同进化中的变量分解示意图Fig.1 Schematic diagram of variable decomposition in cooperative co-evolution frame 为解决现实作战中因大规模变量所导致的“维数灾难”问题,MOPSO-II算法根据“分而治之”的策略,通过引入变量随机分解策略和合作协同框架,将大规模的变量随机分解成若干个维度适中的变量组——子种群,并通过子种群之间的合作协同来求解WTA问题。 2.1 粒子编码与解码 由于MOPSO算法研究的是具有连续变量的数值优化问题,无法直接用于求解WTA多目标规划这一非线性组合优化决策问题,因此,首先需要把解空间上的向量编码成类似遗传算法中基因的形式。 所采用的编码方式不仅要能表示问题的解,还应尽量满足WTA多目标规划模型中所设定的约束条件,为此本文考虑设计了如图2所示的编码结构方案。图2中,武器系统包含有m种型号的导弹,其中第i种型号导弹有ci枚,本文里的编码方案用长为c1+c2+…+cm的整数串来表示一个粒子;其中p1,p2,…,pc1代表第1个武器系统W1所拥有的c1个导弹武器分配方案,pc1+1,pc1+2,…,pc1+c2代表第2个武器系统W2所拥有的c2个导弹武器分配方案,则pc1+c2+…+cm-1+1,pc1+c2+…+cm-1+2,…,pc1+c2+…+cm代表第m个武器系统Wm所拥有的cm个导弹武器分配方案。记粒子的维数为D,也即c1+c2+…+cm=D. 图2 MOPSO-II算法编码结构图Fig.2 Coding structure chart of MOPSO-Ⅱ algorithm 假设WTA火力分配问题中有T1,T2,…,Tn共n个打击目标,故在粒子编码p1,p2,…,pn过程中,每一维的pi取值均限定为0~n的整数,即pi∈[0,n]. 如pi=k,则表示pi所对应的型号导弹分配给了目标Tk,如pi=0,则代表pi所对应的型号导弹本轮没有分配。 由此可知,本文所采用编码方式能够满足(8)式中的约束条件1和条件3. 而约束条件2却并不一定满足,即上述编码方式有可能出现攻击方对拟打击的目标Tj使用导弹数目多于sj的情况。因此在对编码进行初始化和MOPSO-II算法操作产生新粒子时,应检查新粒子是否符合约束条件2,若不满足还需重新初始化粒子直至约束条件2成立为止。 解码时,从左至右依次扫描整个编码。扫描至pk时,首先得到pk所对应的导弹型号i,接着检查pk取值,若pk=0则说明pk所对应型号的导弹没有分配给任何目标;若pk=j则说明pk对应型号的导弹被分配给了第j个目标。 2.2 变量随机分解策略 尽管早期已有合作协同框架的思想,且在解决大规模独立变量方面具有良好的效果,但是当变量之间不再相互独立而是有所联系时,仍然沿用原有框架进行优化的效果变得不再理想。其主要原因是多目标优化问题中,大规模的变量之间往往存在内嵌关联,简单机械地进行变量分解会丢失大量重要的内嵌关联信息,导致优化效果低下。本文采用变量随机分解策略,将D维决策向量组随机分配到K个子元素中,以增加关联变量分到同一组的概率,每个子元素的维度为λ,且满足D=λK,K个子元素均被设成含有NP个粒子的子种群,具体分解过程如图3所示。 图3 变量随机分解过程图Fig.3 Process chart of variable random decomposition 2.3 适应度评价 MOPSO算法在优化武器- 目标分配问题时,需要通过适应度来评价各子种群中单个粒子当前位置的优劣。本文在优化过程中,按照“导弹打击目标的失败概率与粒子适应度呈反比”的思想,以攻击方打击所有目标的失败概率加权和最小为目标,相应的适应度函数为 (11) 式中:向量p*为一个完整的编码方案;qij代表i型导弹攻击目标j的成功概率,qij的值由C3I系统提供。计算适应度函数时,首先对p*进行解码,得到分配方案矩阵,然后利用(11)式对单个粒子的适应度进行计算。 2.4 算法框架描述 首先评估各子种群的适应度,为区分单个粒子适应度函数,定义b(j,z)为子种群适应度函数: (12) 将得到的适应度代入(8)式,可得到目标函数f1(b(j,z))、f2(b(j,z)),首先把编码粒子群随机分解成K个子种群,并按照带精英策略的非支配排序遗传算法(NSGA-II)中的排序方法对子种群各粒子进行非支配排序,随机选择非支配排序等级最高粒子中的一个作为子种群j的最优位置。以子种群2为例,种群间的协同进化过程如图4所示。分别用MOPSO算法从1到K对子种群进行优化,将所求出的各子种群的解进行非支配排序,若满足终止条件,则将各个子种群的最优非支配解作为最终输出结果。若终止条件不满足,则将父代子种群的最优非支配解集保留并转入下一轮迭代。 图4 子种群间的协同示意图Fig.4 Schematic diagram of cooperation between subgroups 为避免算法陷入“局部最优”问题,本文采用经典算法NSGA-II中的拥挤距离排序法,并与一个变异操作算子共同维护外部种群中解的分布。一个粒子的拥挤距离为与其相邻的两个粒子在每个子目标上的距离之和,其值越大说明解集越分散、密度越小、多样性更好。如图5中所示的A、B两点的拥挤距离值为与之对应的矩形长、宽之和,且A点的拥挤距离明显大于B点,说明相较于点B来说,A点周围的解比较稀疏,对外部种群多样性的维持也更为重要,若要在两点之间有所选择,应选择裁掉点B. 图5 基于拥挤距离的多样性策略原理Fig.5 Multifarious tactical principle based on crowding distance 基于上述拥挤距离,若以下两个条件有任何一个满足,便对外部种群进行更新操作:1)内部种群产生的新粒子支配外部种群中的某个或某些粒子;2)外部种群中的粒子数已达到最大容量Nmax. 对外部种群进行更新操作的具体步骤为: 1) 依据目标函数值降序排列所有粒子。 2) 利用(13)式计算每个粒子的拥挤距离: Cd= (13) 式中:n表示目标函数个数;xp与xn为粒子xd的前后两个粒子。 3) 给边界上的两个粒子分配最大的拥挤距离,以保留这两个解,利用边界点强化粒子群搜索的全局性。 4) 判断外部种群规模。若当前外部种群未满,直接添加新的非支配粒子,并删除外部种群中被支配的粒子;若外部种群已满,选择拥挤距离最小的个体进行替代。 2.5 算法流程 MOPSO-II优化算法的流程图如图6所示,具体步骤如下: 1) 初始化D维变量及参数。每个子种群的粒子个数为NP,根据粒子编码方案初始化粒子的位置和速度,计算粒子的适应度值,对粒子进行非支配排序,随机选择非支配等级最高的粒子中的一个作为Gbest,设定最大周期CycleMax,子种群数量NumespMax,种群最大迭代次数GenMax; 2)Cycle=1,周期开始执行,将D维变量随机分成NumespMax个子种群,每个子种群粒子个数为NP; 3)Numesp=1,对第1个子种群进行迭代处理; 4)Gen=1,对子种群进行迭代,以粒子当前位置为个体最优位置,步骤1中的Gbest为全局最优位置,按照(7)式和(8)式更新种群中粒子的速度和位置,用(13)式评价粒子的适应度,按照NSGA-II中的拥挤距离排序法对各粒子进行非支配排序,随机选出非支配等级最高中的一个粒子作为Gbest,更新个体最优和全局最优,进入下一轮的迭代,Gen=Gen+1; 5) 当Gen=GenMax满足时,进行外部种群维护,即Numesp=Numesp+1,跳入下一个子种群处理。在下一个子种群处理过程中,将上一个子种群中得到的Gbest作为全局最优进行更新,其他操作同步骤4; 6) 当Numesp=NumespMax时,重新进行变量随机分解,重复执行步骤3~步骤5; 7) 通常情况下,当Cycle=CycleMax成立时便输出结果,程序结束。 2.6 算法时间复杂度分析 假定优化问题的目标数目为M,划分的子种群数目为S,子种群的粒子规模为N,外部种群规模为N′,则由文献[21-22]可知NSGA-II算法的时间复杂度为O(MS2N2)。MOPSO-II算法的时间复杂度可估计如下: 1) 生成初始粒子群体的时间为O(SN),粒子飞行速度的初始化时间为O(SN),粒子历史最优位置的初始化时间为O(N),按照初始值计算种群中粒子适应度的时间为O(MN),对粒子进行非支配排序的时间为O(SNlnN),为外部种群中的粒子赋予生存期值的时间为O(N′),因此初始化过程总的时间复杂度为O(SNlnN)。 2) 计算子种群中粒子适应度的时间为O(MN),更新粒子历史最优位置的时间亦为O(MN),从外部种群中随机选择全局最优解所需时间为O(MN′),按照NSGA-II算法中的非支配排序方法排序粒子的时间复杂度为O(MN2),执行变异操作的时间复杂度为O(N),选择非支配粒子加入外部种群,并对其进行维护的时间复杂度为O(MNlnN),子种群迭代过程的时间复杂度为O(MN)+O(MN)+O(MN′)+O(MN2)+O(N)+O(MNlnN)=O(MN2),因此,种群的时间复杂度为O(MSN2)。 3) 输出外部种群中所有解个体的时间为O(N′)。因此,MOPSO-II算法的时间复杂度应为O(SNlnN)+O(MSN2)+O(N′)=O(MSN2). 由此可见,相比于NSGA-II算法的时间复杂度O(MS2N2)来说,MOPSO-Ⅱ算法的要小。 为了验证本文所使用的MOPSO-II算法求解多平台WTA问题的有效性及性能,在Intel(R)Core(TM)2 Duo CPU E8600,2.0 GB RAM,Windows XP实验平台上,在Matlab 7.12.0实验环境下进行仿真计算。 假设进攻方有10种不同型号的导弹,需要同时对12个不同类型的目标进行火力打击,战局假设数据如表1所示。 目标的重要度系数和每种型号导弹对各目标的毁伤概率分别由如下威胁系数矩阵和杀伤概率矩阵给出。 表1 战局假设数据 W=[0.12 0.08 0.13 0.14 0.11 0.01 0.06 0.10 0.05 0.04 0.07 0.09], MOPSO-II算法中设置控制参数如下:惯性权重ω=0.9,学习因子C1=C2=2,种群规模的大小为100、200,算法终止的条件为最大迭代次数200,变异概率为0.1,分组大小为50. 程序独立运行20次得到的结果如表2所示。 表2 算法统计结果 MOPSO-II算法和NSGA-II算法求解该实战问题仿真运行时间及仿真结果分别如图7~图9所示。 图7 两种算法运行时间对比图Fig.7 Comparison of running times of two algorithms 图8 NSGA-II算法仿真图Fig.8 Simulation of NSGA-II algorithm 图9 MOPSO-II算法仿真图Fig.9 Simulation of MOPSO-II algorithm 由图7可知,在种群规模较小时,两种算法所花费的运行时间差别不大,但是随着规模的增加,MOPSO-Ⅱ算法的运行效率更高,时间花费更少。当种群规模为300,迭代为200时,仿真结果如图8和图9所示,图中的每个解均代表一种分配方案。例如:f2=19,1-f1=0.14时,其染色体所对应的编码方案为[2 8 1 7 3 9 6 9 6 10 9 10 2 3 6 5 8],导弹与目标分配如表3所示。 由图8和图9可知,两种算法均体现了增加导弹数量对打击目标毁伤效能的影响,都能为决策者提供可靠依据,但图9中的Pareto前沿分布性和收敛性更好,尤其是当0.65 表3 目标分配方案 针对作战中武器- 目标火力分配问题包含众多变量的实际,本文将遗传算法、PSO算法和Pareto集多目标优化算法结合在一起,提出了基于大规模变量随机分解的MOPSO-Ⅱ化算法,并建立了基于毁伤效能最大和用弹量最少两个目标函数的火力分配模型。按照“分而治之”的策略在算法中引入变量随机分解策略和合作协调进化框架,有效克服了传统单目标优化算法效率低下获取权重不易、PSO算法存在“维数灾难”的缺点,实例仿真结果表明MOPSO-Ⅱ算法比NSGA-Ⅱ算法具有更好的求解精度与运行效率,能够获得满意的分配结果且计算快速有效,比较适合较大规模的复杂WTA问题实时求解,但在简化模型结构和避免陷入局部最优方面还有待进一步深入研究。 References) [1] Lloyd S P, W H S. Weapon allocations is NP-complete[C]∥IEEE Summer Conference on simulation. Reno, Nevada: IEEE, 1986:88-95. [2] 许建中. 基于遗传算法的武器目标分配模糊多目标规划[J]. 军事运筹与系统工程, 2010, 24(3):70-74. XU Jian-zhong. Weapon-target assignment with fuzzy multi-objective ranking genetic algorithm[J]. Military Operation Research and System Engineering, 2010, 24(3):70-74.(in Chinese) [3] 袁形形. 遗传多目标优化算法的研究[D]. 北京:中国地质大学, 2010. YUAN Xing-xing. Research of multi-objective evolutionary algorithms[D]. Beijing: China University of Geosciences,2010.(in Chinese) [4] 曲在滨, 刘彦君, 徐晓飞. 用离散粒子群优化算法求解WTA问题[J]. 哈尔滨工业大学学报, 2011, 43 (3):67-69,101. QU Zai-bin, LIU Yan-jun, XU Xiao-fei. Discrete particle swarm optimization for solving WTA problem[J]. Journal of Harbin Institute of Technology, 2011, 43(3):67-69,101.(in Chinese) [5] 肖嵘, 赵成旺, 王护利, 等. 多群协同PSO优化算法的WTA问题求解[J]. 计算机仿真, 2010, 27(9): 12-14, 28. XIAO Rong, ZHAO Cheng-wang, WANG Hu-li, et al. Multi swarms cooperative particle swarm optimization for solving WTA problem[J] Computer Simulation, 2010, 27(9): 12-14,28.(in Chinese) [6] 刘慧慧. 基于多种群协同的多目标粒子群优化算法研究[D]. 南京:南京邮电大学, 2014. LIU Hui-hui. Study on multi-populations for multi-objective optimization PSO algorithm and its application [D]. Nanjing: Nanjing University of Posts and Tele-communications, 2014.(in Chinese) [7] 谢承旺, 李凯, 徐君, 等. 一种改进型多目标粒子群优化算法MOPSO-Ⅱ[J]. 武汉大学学报:理学版, 2014, 60(2):144-150. XIE Cheng-wang, LI Kai, XU Jun, et al. An Improved multi-objective particle swarm optimization algorithm MOPSO-Ⅱ[J]. Journal of Wuhan University: Natural Science Edition, 2014, 60(2):144-150.(in Chinese) [8] Hu X, Eberhart R. Multi-objective optimization using dynamic neighborhood particle swarm optimization[DB/OL]. [2013-02-09]. http:∥www.swarmintelli gence.org/papers/CEC2002 Multi-objective.pdf. [9] Clello C C, Pulido G T, Lechunga M S. Handling multiple objectives with particle swarm optimization [J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3):256-279. [10] 崔莉莉. 基于蚁群算法的武器- 目标分配问题研究[D]. 上海:上海交通大学, 2011. CUI Li-li. Ant colony algorithm for solving the weapon-target assignment problem[D]. Shanghai:Shanghai Jiao Tong University, 2011. (in Chinese) [11] 张毅, 杨秀霞, 周绍磊. 基于量子分布估计算法的火力分配问题研究[J]. 电光与控制, 2013, 20(12):18-21. ZHANG Yi, YANG Xiu-xia, ZHOU Shao-lei. Fire assignment based on quantum-inspired estimation of distribution algorithm[J]. Electronics Optics & Control, 2013, 20(12):18-21.(in Chinese) [12] 阮旻智, 李庆民, 刘天华. 编队防空火力分配建模及其优化方法研究[J]. 兵工学报, 2010, 31(11):1525-1529. RUAN Min-zhi, LI Qing-min, LIU Tian-hua. Modeling and optimization on fleet antiaircraft firepower allocation[J]. Acta Armammentarii, 2010, 31(11):1525-1529.(in Chinese) [13] 张海兵, 徐诚, 李世永. 贪心遗传算法及其在武器目标分配问题中的应用[J]. 弹道学报, 2007, 19(2):40-43. ZHANG Hai-bing, XU Cheng, LI Shi-yong. GGA and its application to weapon target assignment[J]. Journal of Ballistics, 2007,19(2): 40-43.(in Chinese) [14] 丁铸, 马大为, 于存贵, 等. 基于禁忌搜索与微粒群优化算法的混合优化策略算法在目标分配问题上的应用[J]. 兵工学报, 2007, 28(9):1127-1131. DING Zhu, MA Da-wei, YU Cun-gui, et al. Application of hybrid optimization strategy algorithm based on tabu search and particle swarm optimization algorithms for weapon- target assignment problems[J]. Acta Armamment-arii, 2007, 28(9):1127-1131.(in Chinese) [15] 麻士东, 龚光红, 韩亮, 等. 目标分配的蚁群- 模拟退火算法及其改进[J]. 系统工程与电子技术, 2011, 33 (5):1182-1186. MA Shi-dong, GONG Guang-hong, HAN Liang, et al. Hybrid strategy with ant colony and simulated annealing algorithm and its improvement in target assignment[J]. Systems Engineering and Electronics, 2011, 33(5):1182-1186.(in Chinese) [16] 郭业才, 张苗青. 基于混合蛙跳算法的多模盲均横算法[J]. 兵工学报, 2015, 36(7):1280-1287. GUO Ye-cai, ZHANG Miao-qing. A multi-modulus blind equalization algorithm based on shuffled frog leaping algorithm of hybrid optimization[J]. Acta Armammentarii, 2015, 36(7):1280-1287.(in Chinese) [17] Potter M A, De Jong K A. A cooperative co-evolutionary approach to function optimization, parallel problem solving from nature, PPSN III[J]. Lecture Notes in Computer Science, 1994, 866: 249-257. [18] Kennedy J, Eberhart R. Particle swarm optimization[C]∥1995 IEEE International Conference on Neural Networks. Piscataway, NJ, US:IEEE, 1995:1942- 1948. [19] Li X, Yao X. Cooperatively coevolving particle swarms for large scale optimization[J]. IEEE Transactions on Evolutionary Computation, 2012, 16(2):271-289. [20] Antonio L M, Coello C. Use of cooperative co-evolution for solving large scale multi-objective optimization problems[C] ∥2013 IEEE Congress on Evolutionary Computation. Cancun, Mexico:IEEE, 2013: 2758-2765. [21] Deb K, Pratab A, Agarwal S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ [J]. IEEE Transactions on Evolutionary Computation, 2002, 4(6):182-197. [22] Ahuja R K, Kumar A, Jha K C, et al. Exact and heuristic algorithms for the weapon-target assignment problem[J]. Operations Research, 2007, 55(6):1136-1146. Weapon-target Assignment with an Improved Multi-objective Particle Swarm Optimization Algorithm XIA Wei1, LIU Xin-xue1, FAN Yang-tao1, YUAN Feng-gang2 (1.Elementary Command College, Rocket Force University of Engineering, Xi’an 710025, Shaanxi, China; 2.Unit 91033 of PLA, Qingdao 266034, Shandong, China) Weapon-target assignment (WTA) with numerous variables in modern campaign is a typical non-deterministic polynomial (NP) complete problem. An optimization model based on improved multi-objective swarm optimization algorithm (MOPSO-II) is established to solve the objective functions of maximum damage probability and minimum ammunition consumption. Since “curse of dimensionality” occurs in the objective swarm optimization algorithm (PSO), the random variable decomposition strategy and cooperative co-evolution evolutionary frame are used for variable decomposition, and also all swarms are composited by using the non-dominated set algorithm in NSGA-II. The simulated results show that MOPSO-II is quicker and more effective than NSGA-II, and can give good WTA quickly, especially when the scale of WTA problem is large. ordnance science and technology; multi-objective optimization; particle swarm optimization; firepower distribution; Pareto set; weapon-target assignment 2016-01-07 国家自然科学基金青年基金项目(61304001) 夏维(1982—),男,博士研究生。E-mail:xiawei66@163.com; 刘新学(1964—),男,教授,博士生导师。E-mail:liyax@sina.com E920.8 A 1000-1093(2016)11-2085-09 10.3969/j.issn.1000-1093.2016.11.017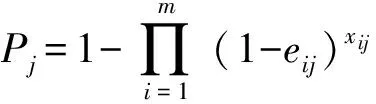
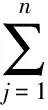
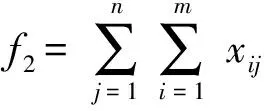
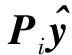

2 MOPSO-Ⅱ算法
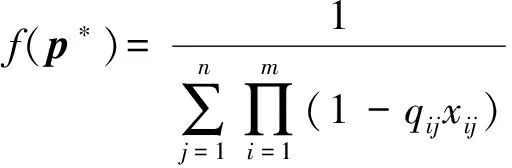
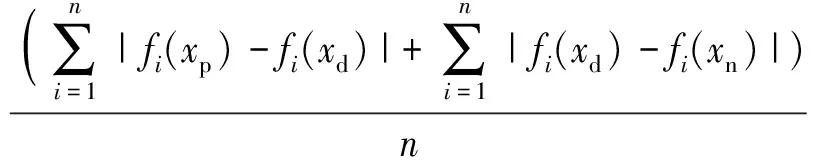
3 仿真及算例分析

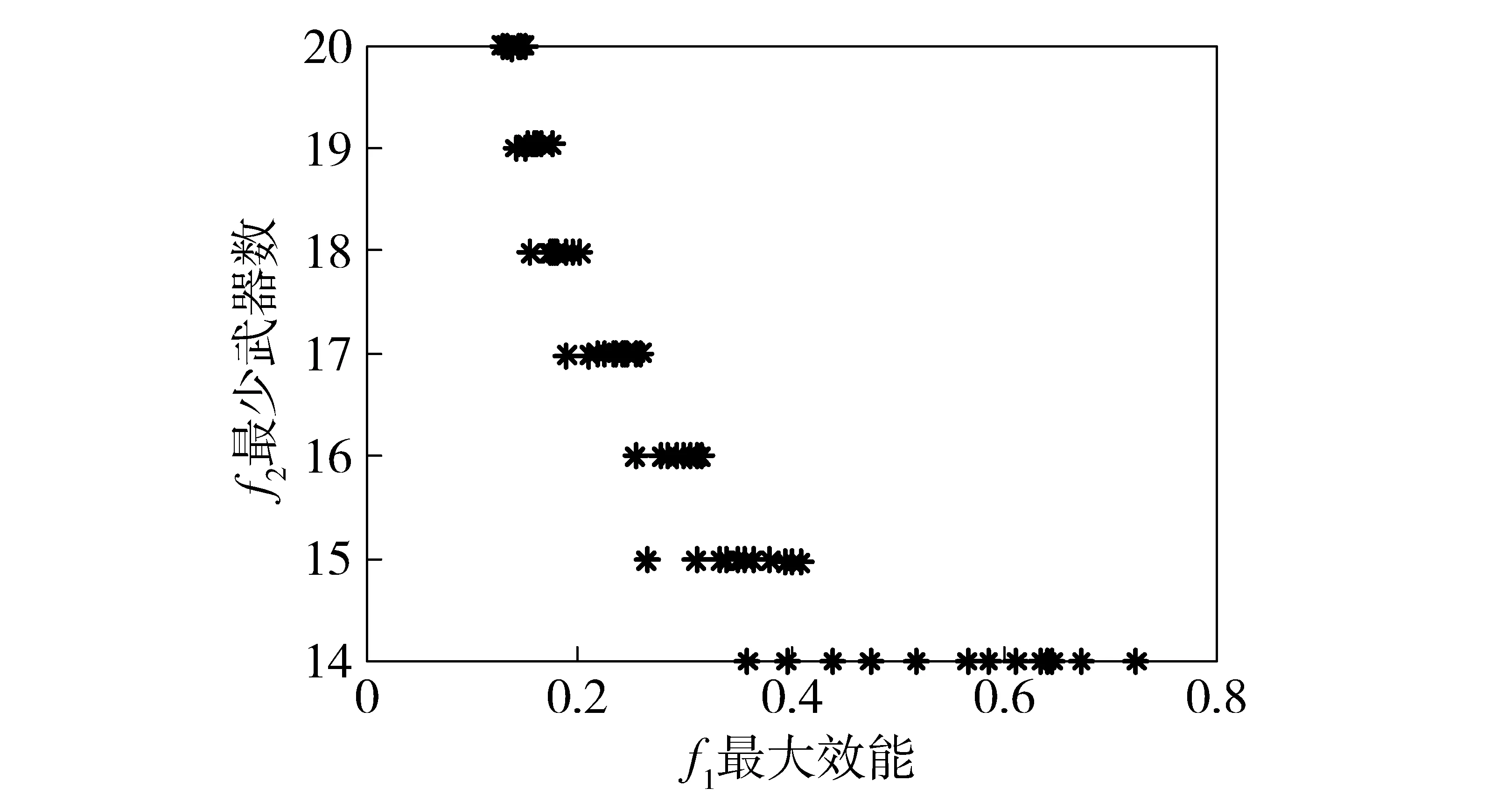
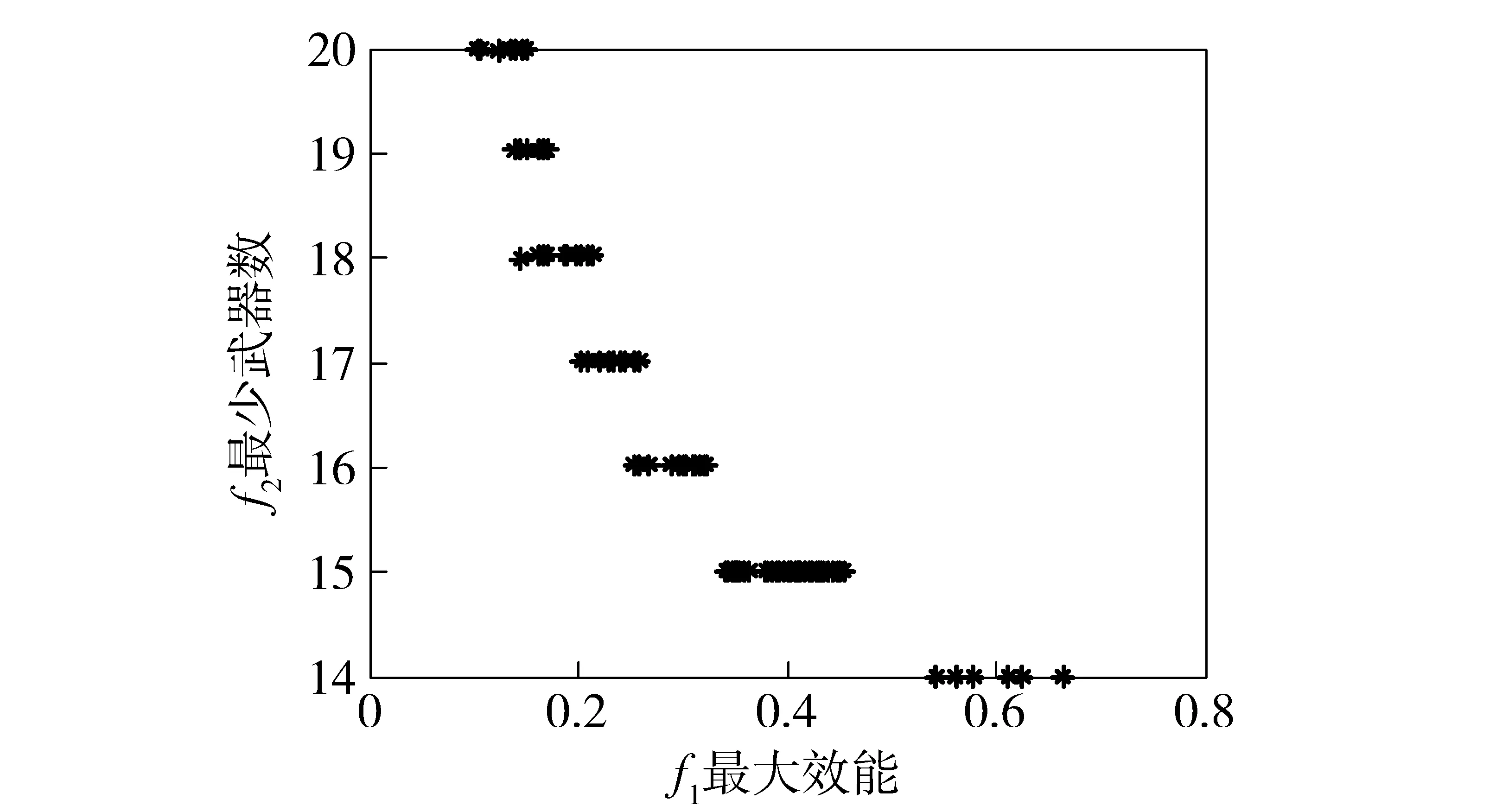
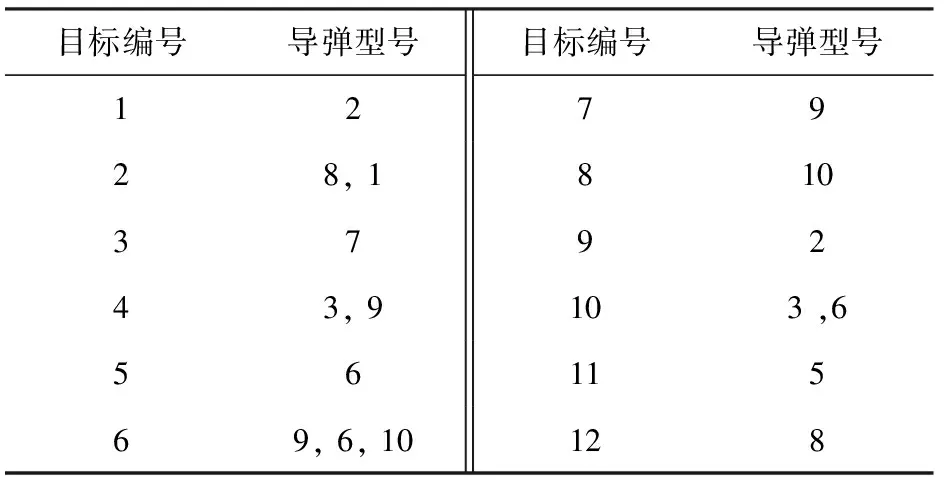
4 结论

