某大口径火炮系列杀爆弹地面密集度影响因素回归分析

朱乐乐，王雨时，刘锦春

(1.南京理工大学 机械工程学院， 南京 210094； 2.兵器工业第一二三厂，黑龙江 齐齐哈尔 161000)

杀爆弹即杀伤爆破弹，简称榴弹，是现代战争中应用最为广泛的一种炮兵弹药，它既可以有效杀伤敌方有生力量，又能摧毁敌方防御工事。射击精度是杀爆弹的重要战术技术指标，包括地面密集度和射击准确度两方面。地面密集度反映了在相同射击条件下弹着点对于平均弹着点的密集程度，通常用中间误差或中间误差与射程的比值表示。地面密集度分为纵向密集度和横向密集度[5]；射击准确度用来表征射弹的平均弹着点相对瞄准点或目标的偏差，由武器系统自身的特性决定，可通过弹道修正理论修正。射击密集度是射击准确度的基础。目前，杀爆弹的射击精度研究主要集中在如何提高地面密集度方面。文献[1]利用均匀设计的方法，通过回归分析研究随机因素对弹丸地面密集度的影响，得到了地面密集度的主要影响因素及其影响程度。文献[2]对影响射击精度的各种射击环境参数进行分析，研究了计算机仿真射击精度的方法。文献[3]基于仿真火炮发射全过程从而预测立靶散布的基本原理，研制出了某自行高炮车炮系统地面密集度预测软件。文献[4]以某车载炮密集度性能实弹射击试验数据为基础，采用逐步回归分析法研究了初速、弹丸质量和偏心距等因素对车载炮射击密集度的影响。结果表明，影响纵向射程的主要因素是初速，而影响横向侧偏的主要因素是弹重。文献[5]综述了中大口径火炮地面密集度研究现状，总结了火炮地面密集度的研究方法和进展。文献[6]运用最优拉丁超立方试验方法进行了地面密集度灵敏度计算，通过回归分析与方差分析获得了影响地面密集度的主要因素，以及各随机因素对地面密集度的影响规律。

进行靶场实弹射击时，常出现地面密集度不理想的情况。若能通过多元回归分析，对可能影响地面密集度的因素进行研究，找出影响弹丸地面密集度的主要因素，并进行控制，就可以达到提高弹丸地面密集度的目的。SPSS(statistical product and service solutions)是当今流行的数据分析软件之一，专业化程度很高，可用于统计学分析运算、数据挖掘和预测分析等。本文利用SPSS软件对某大口径火炮所配两种类型杀爆弹(即枣核底凹杀爆弹、圆柱底凹杀爆弹)靶场射击试验数据进行多元线性回归分析，分别建立关于横向密集度和纵向密集度的回归方程，并进一步分析各影响因素对地面密集度的影响程度(权重)。分析结果可为该系列杀爆弹的地面密集度评价、质量监控和改进设计等提供参考。

1 逐步回归算法

多元线性回归法是一种在线性相关的前提下，分析两种及两种以上自变量和因变量的数量关系的方法。多元线性回归模型一般为：

y=b+b1x1+b2x2+…+bnxn

(1)

式(1)中：y为因变量；x1、x2、…、xn为自变量；b为常数项，b1、b2、…、bn为偏回归系数。

逐步回归法是多元回归分析中的一种常用算法，可以在多因素综合作用情况下，分析众多因素中各因素对因变量的影响程度。该方法常用来分析众多因素中无法确定究竟是哪些因素对因变量有影响的情况，在数据分析中应用广泛。其最大特点是在引入或剔除一个变量时都要进行F检验。具体流程为根据向前选择法则引入自变量，然后根据向后剔除法则将回归方程中F检验概率最小且符合剔除条件的自变量剔除，重复进行上述引入和剔除过程直到回归方程外的自变量均不符合引入条件、回归方程中的变量均不符合剔除条件[7]。

2 某大口径火炮所配两种杀爆弹地面密集度影响因素回归分析

2.1 枣核底凹杀爆弹地面密集度影响因素回归分析

表1列出了6组(每组7发)某大口径火炮枣核底凹杀爆弹地面密集度试验的试验条件数据和地面密集度数值。对可能影响地面密集度的试验条件因素编号如下：弹丸平均质量X1、质量极差X2、质量均方差X3、平均质心位置X4、质心位置极差X5、质心位置均方差X6、平均偏心距X7、偏心距极差X8、偏心距均方差X9、平均极转动惯量X10、极转动惯量极差X11、极转动惯量均方差X12、平均赤道转动惯量X13、赤道转动惯量极差X14、赤道转动惯量均方差X15、平均赤极比X16、赤极比极差X17、赤极比均方差X18、初速X19、初速或然误差X20、射程X21。下面应用多元回归算法分别研究该型杀爆弹横向密集度和纵向密集度的主要影响因素。

表1 某大口径火炮枣核底凹杀爆弹地面密集度试验数据

续表1 某大口径火炮枣核底凹杀爆弹地面密集度试验数据

1) 纵向密集度Ex/X影响因素回归分析

由于进行多元线性回归分析的前提是变量间需线性相关，由此，首先对表1中的数据进行相关分析，得到纵向密集度Ex/X与各影响因素的线性相关系数。表2仅列出了与纵向密集度Ex/X的线性相关系数绝对值大于0.3的影响因素，在后面分析中不再考虑线性相关系数绝对值小于0.3的影响因素。

以表2中的各因素为自变量，纵向密集度Ex/X为因变量进行逐步回归分析。令纵向密集度Ex/X为y1，引入和剔除变量过程F检验标准默认分别取0.05和0.1时，没有变量进入回归方程。此时，可将F检验标准的标准放宽到0.1，得到的回归方程为：

y1=0.689-0.015X1

(2)

可见，该方程中仅有弹丸平均质量一个自变量。说明在众多影响因素中，该型弹丸纵向密集度Ex/X只与弹丸平均质量有关，且二者是负相关。因此，适当增大弹丸质量可提高其纵向密集度。

2) 横向密集度Ez影响因素回归分析

对表1数据进行相关分析，得到横向密集度Ez与各因素的线性相关系数。表3中列出了与横向密集度Ez相关系数绝对值大于0.3的影响因素。

表2 某大口径火炮枣核底凹杀爆弹地面密集度各影响因素与Ex/X的线性相关系数

表3 某大口径火炮枣核底凹杀爆弹地面密集度各影响因素与Ez的线性相关系数

以表3中的各因素为自变量，横向密集度Ez为因变量进行线性回归分析。令横向密集度Ez为y2，当引入和剔除变量过程F检验标准分别取0.05和0.1时，得到的回归方程为：

y2=-0.013+1.61X6

(3)

由式(3)可知，某大口径火炮枣核底凹杀爆弹横向密集度Ez主要弹丸质心位置均方差有关，且二者呈正相关。因此，可以通过控制弹丸质心位置散布的方法提高该型弹丸的横向密集度。

2.2 圆柱底凹杀爆弹地面密集度影响因素回归分析

某大口径火炮圆柱底凹杀爆弹的靶场试验条件数据和试验结果如表4、表5所示。共进行7组试验(每组7发)。表4中变量的编号与前面相同。下面使用SPSS软件分别对该型杀爆弹横向密集度和纵向密集度的主要影响因素进行回归分析。

对表4、表5中的数据进行相关分析，得到该圆柱底凹杀爆弹纵向密集度Ex/X、横向密集度Ez与各因素的线性相关系数。表6和表7分别列出了相关系数绝对值大于0.3的影响因素。

以表6中的各因素为自变量，纵向密集度Ex/X为因变量进行线性回归分析。令纵向密集度Ex/X为y3。当引入和剔除变量过程F检验标准分别取取0.05和0.1时，没有变量符合引入标准。此时，可将引入变量时F检验的标准增加到0.1。得到的回归方程如下：

y3=-0.365+0.001X4

(4)

由式(4)可知，影响某大口径火炮圆柱底凹杀爆弹纵向密集度Ex/X的主要因素为平均质心位置。因此，可以通过降低弹丸质心位置来提高该型弹丸的纵向密集度。

再以表7中的各因素为自变量，横向密集度Ez为因变量进行线性回归分析。令横向密集度Ez为y4。当引入和剔除变量过程F检验标准分别取0.05和0.1时，仍没有变量符合引入的标准。将引入变量时F检验的标准增大到0.1后，得到的多元线性回归方程为：

y4=-50.298+28.312X13

(5)

可见，影响某大口径火炮圆柱底凹杀爆弹横向密集度Ez的主要因素为平均赤道转动惯量。赤道转动惯量越小，越有利于提高其横向密集度。

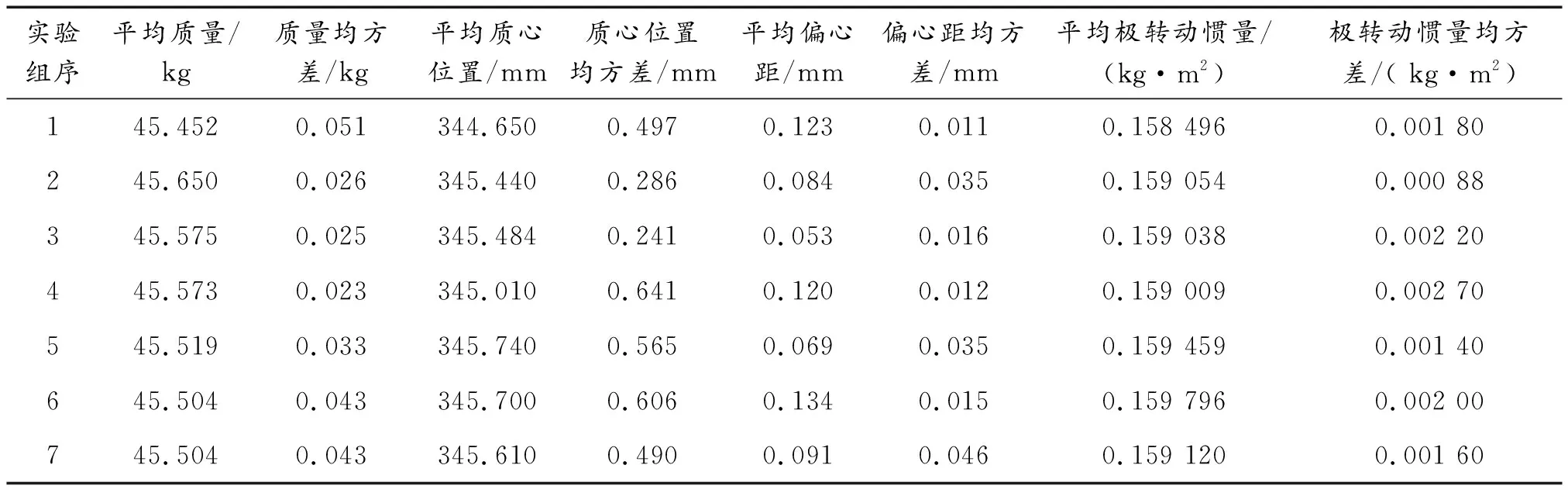
表4 某大口径火炮圆柱底凹杀爆弹地面密集度试验数据之一

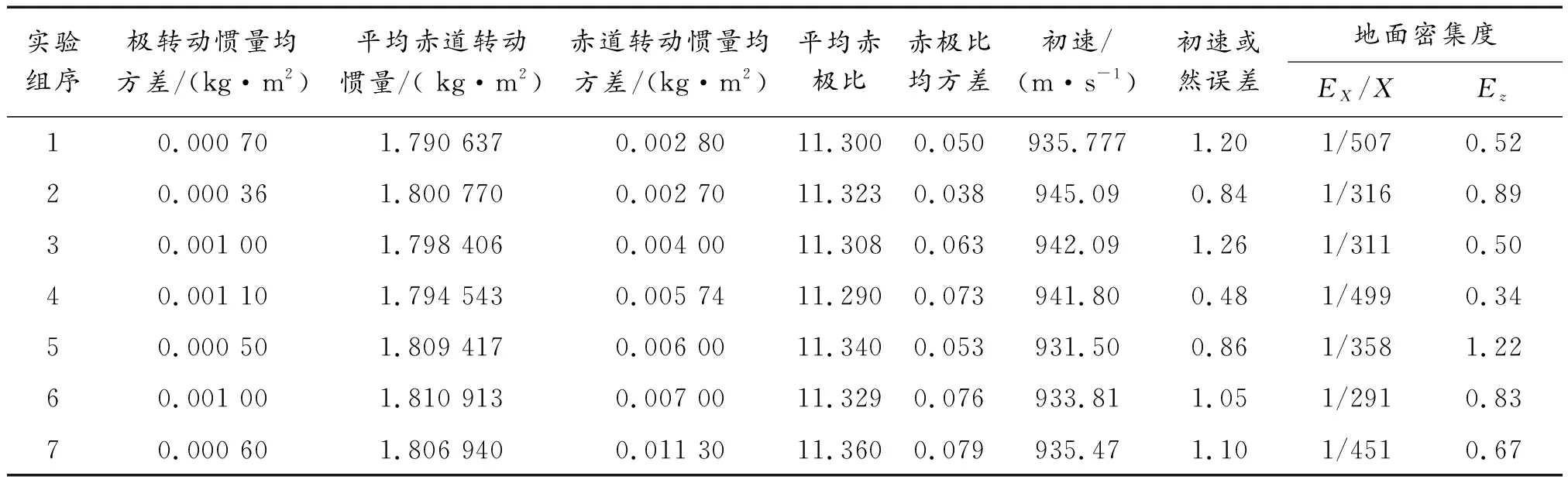
表5 某大口径火炮圆柱底凹杀爆弹地面密集度试验数据之二

表6 某大口径火炮圆柱底凹杀爆弹地面密集度各影响因素与Ex/X的线性相关系数

表7 某大口径火炮圆柱底凹杀爆弹地面密集度各影响因素与Ez的线性相关系数

3 结论

在相同的发射条件下，某大口径火炮所配两种不同类型杀爆弹地面密集度的主要影响因素各不相同。影响枣核底凹杀爆弹纵向密集度的主要因素是平均弹丸质量，影响其横向密集度的主要因素为弹丸质心位置均方差。因此，可以通过增大弹丸质量并减小弹丸质心位置散布的方法提高该型弹丸地面密集度。圆柱底凹杀爆弹纵向密集度主要与平均质心位置有关，横向密集度主要与平均赤道转动惯量有关。可通过降低弹丸质心位置和减小赤道转动惯量来提高该型杀爆弹的地面密集度。可见，两种类型杀爆弹的地面密集度都与弹丸的质量属性有很大关系。上述分析结果可为该系列杀爆弹的地面密集度评价、质量监控和改进设计等提供参考。