例说科学精神

彭翕成刘玉琴

例说科学精神

彭翕成刘玉琴

一、什么是科学精神？

这两年，核心素养一词十分火热。每个学科根据学科特点，建立了自己的一套体系。譬如数学学科，很多文章都大谈6个关键词：数学抽象、直观想象、逻辑推理、数学运算、数学建模、数据分析，却忽视了一个基本事实，各学科的核心素养是建立在《中国学生发展核心素养》这一总纲的基础上。

学生发展核心素养，是指学生应具备的、能够适应终身发展和社会发展需要的必备品格与关键能力，综合表现为9大素养，具体为社会责任、国家认同、国际理解、人文底蕴、科学精神、审美情趣、身心健康、学会学习、实践创新。

这9大素养看起来有点抽象，但都有具体的解释，有兴趣的读者可上网搜索。其中科学精神是指个体在学习、理解、运用科学知识和技能等方面表现出的价值标准、思维方式和行为规范，包括三个方面：

一是崇尚真知。重点是学习科学技术知识和成果，掌握基本的科学方法，有真理面前人人平等的意识等。

二是理性思维。重点是尊重事实和证据，有实证意识和严谨的求知态度；理性务实，逻辑清晰，能运用科学的思维方式认识事物、解决问题、规范行为等。

三是勇于探究。重点是有百折不挠的探索精神，能够提出问题、形成假设，并通过科学方法检验求证、得出结论等。

而在实践创新中也有一条：批判质疑。重点是具有好奇心和想象力，敢于质疑；善于提出新观点、新方法、新设想，并进行理性分析，做出独立判断等。

二、为何要如此凸显科学精神？

为何《中国学生发展核心素养》要如此凸显科学精神？一方面是由于科学精神本身重要，另一方面则是由于我们这些年的教育教学实在太缺这个了。

儒家传统思想使得国人的性格谨慎、保守,也形成了从众文化。“人随大群不挨罚”“枪打出头鸟”等俗语是人们从众思想的体现。在这样的思想的影响下，人们很难发表自己的不同意见。

在家庭教育中，绝大多数家长都希望孩子“听话”。当孩子的行为与父母的想法一致时，孩子会得到精神和物质上的奖励，否则就会受到一定的惩罚。

在学校教育中，老师处于主体地位。学生如果对老师所授知识产生怀疑，就会被认为是挑战权威，多数时候不会被老师喜欢。在当前教育环境下，“题海战术”的训练使得学生在遇到问题时往往程式化、固定化思考，缺乏个性化的思考与变通。

相对于学生对课本知识的良好掌握来说，目前学生独立思考、发现问题、自我探究、创新意识等方面相对薄弱。这都可以归于科学精神这一块。既然认识到缺乏，就需要好好地补。

培养学生的科学精神是一个长期的教学目标，教育工作者需要不断学习和探讨。笔者认为，只要教师加以重视，选取合适的教学案例，采用探究的眼光、开放的心态，无需另外增加课时专门培养学生的科学精神，在日常教学中完全可以逐步渗透。

三、通过案例理解科学精神。

如果给出下面的三角形，问：下一行应该填什么？想必很多人都会填写1 4 6 4 1，因为规律很明显，不就是杨辉三角么？

而有3个外国中学生给出了不同的答案：1 4 5 4 1，他们的文章《The Rascal Triangle》发表在2010年的《THE COLLEGE MATHEMATICS JOURNAL》。

文章先是设计了一个教学场景（3个作者不是一所学校的），老师很不满意他们给出的答案1 4 5 4 1，告诉他们3+3应该等于6，而不是等于5。

学生解释：我们定义的规则有所不同，除了每行两端都为1之外，其余每个数都等于肩上两数相乘，再加1，然后除以头顶上（即再上一行对应位置上）的数，譬如第5行的

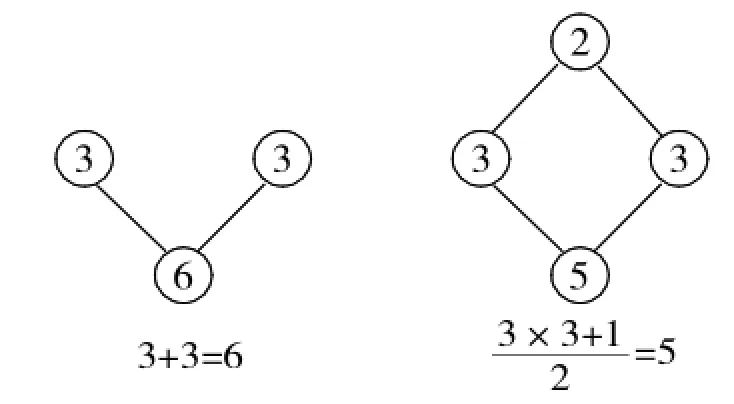
老师提出疑问，所给规则最后用到除法，那能否保证生成的数阵中每一个数都是整数？如果是杨辉三角，那就简单，整数相加总是整数。而若所得不是整数，则这样的定义规则显然是不完美的。

学生给出了巧妙的证明。将数阵旋转45°，得

这样一来，数阵中的每一个位置对应哪个数就更好表述了。行数列数都从0开始，则第m行第n列的数是mn+1，第m行为：1，m+1，2m+1，…，nm+1。

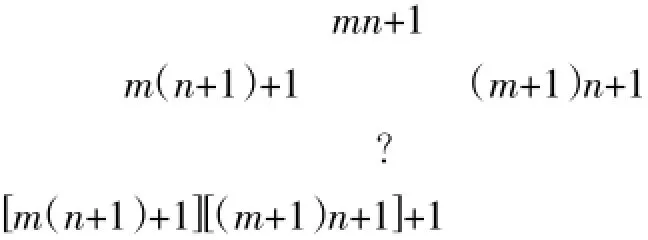
上式除以mn+1，所得（m+1）（n+1）+1正好是第m+1行第n+1列的数。根据数学归纳法可知所有数都是整数。

作为老师，看到学生能有这样的创新，心里自然是高兴的。但可能也会有点担心，要是考试出这样的题目怎么办呢？对这种所谓的数字规律题，相关主管部门要引起重视为好。要么取消这种题目，要么将之作为主观题，只要考生写出自己认为的规律，能够自圆其说，都要视情况给分。

有人去微软公司面试，面试官提出了这样的问题：有一个直角三角形，斜边长10cm，从顶点向斜边作垂线，垂线长6cm（如右图），求直角三角形的面积。

后来这道题被媒体报道，广泛传播，绝大多数网友在第一时间都没看出其中的问题，认为这题真简单，不就是底乘高的一半么？

事实上此题的正确答案是，符合题意的三角形不存在，直角三角形斜边上的高的长度应该不超过斜边的一半，如果作出以AC为直径的圆，以及AC中点O（即圆心）就更清楚了。这提醒我们考试时不能总默认为题目都是对的，有时考的就是大家的挑错能力。

圆周率永远不尽的神话，已被加拿大一名年仅17岁的少年天才打破了。在一则标题为《圆周率并非无穷无尽》的消息中说，“加拿大少年天才伯西瓦在今年6月运用电子邮件与世界上的25台超级电脑连接，利用二进位算法，发现了圆周率第5兆位的小数是零。也就是说，如果按十进位来算，圆周率的第1兆2千5百亿位数应是它的尽头”。这表明圆周率是可以除尽的。消息中还称，“在去年9月，法国人贝拉尔已把π算到第1兆（106）位小数，并由此创下了世界纪录”。

1999年，首都师范大学的学科教学论研究生入学考试选用上述素材（摘自1998年的《科技日报》）出了一道开放性题：请你用数学教育理论对上述报道进行分析，谈谈自己的看法。

有人可能会说：研究生考试考这个？这么简单的送分题！初中生都知道圆周率是无理数啊，怎么可能除尽？

答题结果让人大跌眼镜。19份答卷中，只有4份答卷指出“这则报道是荒谬的，‘圆周率是无理数’是科学真理，计算机不可能把它除尽”。有2份答卷表示担心：“如果圆周率是有理数，以后中学有理数怎么教？”其余13份答卷则大谈“在未来的信息社会，技术进步使什么奇迹都可以创造出来。圆周率是有理数，这是科学进步的标志。人们要更新观念，才能跟上时代的步伐”。这13份答卷表明这些学生既缺乏批判精神，也缺乏实事求是、坚持真理的勇气。

按理说，1999年报考首都师大研究生的考生水平应该还可以。因为当时研究生招生人数少，录取率低，考研的还是大学生中的优秀者。最大的可能是：1999年，中国电脑普及率很低，大家都觉得电脑非常先进神秘，加上提及加拿大、法国、世界纪录、25台超级电脑这些高大上的词，考生都不敢去质疑。如果去掉这些华丽包装，简单出一道判断题：圆周率是有理数。我武断地说一句，这19位考研学生会百分之百打×。这也就是说，一些外在包装将一个原本很容易判别的命题变得难以判别。

网络上流传这样一个通货膨胀的数学解释：1元=1分。

证明：1元=100分=10分×10分=0.1元×0.1元=0.01元=1分。

上述推导显然存在错误。众所周知，1元=100分=10分×10。

造成错误的原因是忽视了单位的计算。在数学教学当中，计算过程中是不写单位的，只是在计算结束后直接加上单位。教学中对单位运算的忽视，导致一些网友明知上述推导有误，但说不清楚错在哪。

边长为1米的正方形的面积为1平方米，如何计算得到呢？

正方形面积等于边长乘以边长，即1米×1米=（1×1）（米×米）=1平方米。

从这个例子看出，单位也是要参与运算的。

譬如，知道1米=10分米，就可以推导1平方米=1米×1米=10分米×10分米=（10×10）（分米×分米）=100平方分米。这样平方米和平方分米之间的换算就比较清楚，无需死记硬背。

量纲是个物理概念，在数学中出现较少。事实上，我们从小就开始接触了，上述推导就隐藏量纲分析的思想。

量纲是代表物理量性质的符号，是物理量广义的度量。任何一个物理量，不论选取什么度量单位，都具有相同的量纲。例如尺子的长度，不论用米还是厘米，都代表长度的单位，具有相同的量纲。

数学除了演绎推理，大胆猜测也很重要。猜测要讲究技巧和方法，量纲分析就是需要掌握的一个基本方法。下面来看两道看似风马牛不相及的题目。

一艘船上有45只牛，32只羊，那么船长几岁？

这道题流传很广。很多人利用45和32这两个数拼凑出各种各样稀奇古怪的结果。

直角△ABC中，E是斜边AB上一点，AE=a米，EB=b米，四边形DEFC是正方形，求阴影部分的面积。

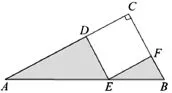
从不同中看出相同，不大容易。这两题有两大相同：一是可以从量纲角度，从条件到结论进行推理；二是题目只有两个已知数据，能变化的可能性有限。

船长的年龄问题，学生给出最多的答案是45+32=77。小学生在只学了加减乘除的情况下，这可能是相对合理的答案了。暂且不管牛和羊是否可以这样相加，就算是加上了所得单位也是“只”，不是“岁”。从小学到大学，甚至到研究生，我们都从未听闻过从“只”这个单位推理到“岁”这个单位。答案要正确，除了数字要对得上，还要求量纲也要对得上。量纲对不上，则可认为答案也是错误的。

已知AE和EB长度单位是米，所求面积的单位自然就是平方米。如何得到平方米，两个数据相加、相减所得单位还是米，两个数据相除的话单位会被消去，自然是不行的。最容易想到的就是两个数据相乘。从量纲角度看，是符合的。两线段相乘，几何意义就是以这两条线段为边作长方形的面积。考虑a=b这种特殊情形，那么可猜测所求阴影部分的面积应该是平方米。

上述分析也提醒我们，可考虑绕E为中心将△BEF旋转90°。这样可以得到一种比较可行的解法而不是猜想。要提醒注意的是，需要证明旋转后的点B刚好落在AC上。

网上有文章专门分析这一问题。在文章《为什么人民币没有3元？》中有这样一段：

货币面值是依据数学的组合原理设计的。在数字1到10里，有重要数和非重要数之分，1，2，5，10就是重要数，用这几个数能以最少的加减运算得到另外一些数。如1+2=3，2+2=4，1+5=6，2+5=7，10-2 =8，10-1=9，其余的就是非重要数。而如果将4个重要数中的任意一个用非重要数代替，就出现有的数要相加或相减两次才能得到，比较繁琐。

这段分析看起来像那么回事，但经不起推敲。假设用1，3，5代替1，2，5会出现什么情况，真的会更麻烦么？此处不考虑10，因为10，20，50可看作10倍后的1，2，5。同理适用于1角，2角，5角。

用1，2，5表示1～9，最少需要17张人民币。表示1需要1张，表示2需要1张，表示3需要2张，表示4需要2张，表示5需要1张，表示6需要2张，表示7需要2张，表示8需要3张，表示9需要3张。

用1，3，5表示1～9，最少需要17张人民币。表示1需要1张，表示2需要2张，表示3需要1张，表示4需要2张，表示5需要1张，表示6需要2张，表示7需要3张，表示8需要2张，表示9需要3张。

以上只考虑加法，如果加上10，且考虑减法，3也不比2差，请看：2=1+1，4=3+1，6=5+1，7=10-3，8=5+3，9=10-1。所以认为2比3更重要，从而没有3元币值这一说法是站不住脚的。

1，2，5中，1是最基本的数，如果没有1，就难以谈其他。至于5，从数学上讲不如1重要，只是人的手指是5个，习惯用十进制，所以5相对重要。至于2，实在看不出哪里比3重要。

在中国古代或是其他国家也都有使用3元币值的。中国第二套人民币中有3元币值，后来取消了，是有历史原因的。之所以有3元币值，是因为当时苏联有3元币值，中国向苏联学习。后来中苏关系破裂，1964年，苏联利用手中的印版继续印刷3元币值，扰乱中国金融秩序。所以中国从此停止使用3元币值。

不只一次看到这篇文章：

如果令A，B，C，D……X，Y，Z这26个英文字母，分别等于1，2，3，4……24，25，26这26个数值，那么如何才能得到圆满的100分呢？

HARD WORK（努力工作）：H+A+R+D+W+O+R +K=8+1+18+4+23+15+18+11=98；

KNOWLEDGE（知识）：K+N+O+W+L+E+D+G+E =11+14+15+23+12+5+4+7+5=96；

LOVE（爱情）：L+O+V+E=12+15+22+5=54；

LUCK（好运）：L+U+C+K=47。

这些我们通常非常看重的东西都不是最圆满的，虽然它们非常重要，那么，什么能使生活变得圆满？

是MONEY（金钱）吗？不！M+O+N+E+Y=13+15 +14+5+25=72。

是LEADERSHIP（领导能力）吗？不！L+E+A+D+E +R+S+H+I+P=12+5+1+4+5+18+19+8+9+16=97。

那么，究竟什么能使生活变得圆满呢？是ATTITUDE（态度），A+T+T+I+T+U+D+E=1+20+20+9 +20+21+4+5=100。

正是我们对待生活的态度，能够使我们的生活达到100分的圆满。你用什么态度去看待世界，你就会得到什么样的世界。

第一次看到这篇文章，我就觉得十分可笑。后来看到很多报刊发表类似的文章，很多网友也转发，心里很纳闷，这玩意还真有人信。这个文章有没有道理呢？

大胆猜测一下，始作俑者是从“态度决定一切”这句话出发，无意中发现规律：A+T+T+I+T+U+D+E= 1+20+20+9+20+21+4+5=100，于是从结果出发去做假设。至于将HARD WORK、KNOWLEDGE、LOVE、LUCK这些词拿来比较，只不过做做样子罢了。

设26个字母对应26个数字，当然可以。从数学角度来看，我们可以提出任何的假设，并基于这些假设进行推理，问题是得到100之后，将100和圆满等同起来，就有偷换概念的嫌疑。就算100=圆满，英文单词数以万计，那么真的只有态度（ATTITUDE）能打100分吗？

尝试一下创新（innovate），9+14+14+15+22+1+20 +5=100。

尝试一下研究员（researcher），18+5+19+5+1+18 +3+8+5+18=100。

尝试一下inflation，9+14+6+12+1+20+9+15+14 =100。这个词意思很多，如膨胀、通货膨胀、夸张、自命不凡。

如果我们使用计算机编程查找，相信还可以找到更多可以得满分的词，这些词都是圆满的么？从常识来看，除去较短和较长的单词，多数单词由5到10个字母组成，那么这些加数凑成100的可能性是比较大的，很难说是唯一的。人生会遇到种种困难，很多时候并不仅靠着乐观的态度就能度过的，还需要其他，譬如努力学习，努力工作，有时还要靠点运气。网络上，心灵鸡汤式的文章多矣。这些鸡汤式文章充满知识、智慧和感情，温暖人心，充满正能量。偶尔读之无妨，若盲目迷信，沉溺其中，则难免有害。

填空题：哈佛大学的校训是______。

说实话，我答不上来。我除了知道哈佛大学是美国名校之外，其余几乎没有什么认知。譬如它在美国哪个州，有哪些优势学科，校友中得了多少次诺贝尔奖，出了多少位美国总统……我一概不知。

但此时，你若出一道判断题：

哈佛大学校友有得过诺贝尔奖的。（）

我会打√，虽然我也说不出是谁得了。如果给点时间去查资料，我会更有把握一些。但即使不查资料，我也会打√。虽然这种直觉有时也会犯错。

再出一道判断题：

哈佛大学的校训：此刻打盹，你将做梦，而此刻学习，你将圆梦。（）

我会打×。即使我不知道哈佛大学的校训是什么，但设身处地地想，我若是一所学校的校长，哪怕只是一所乡村小学的，我也不会将这句话作为校训。道理很简单，把这句话作为校训，让人感觉这所学校的学生很喜欢睡觉。如果学生上课打盹，老师叫醒他，来这么一句，我会觉得这个老师很有水平。但将之作为校训，实在不妥。这是常识！

以我们学生时代的考试经验，计算题比填空题难，因为计算题不仅要结果，还要过程；填空题比选择题难，因为填空题没有备选答案；选择题比判断题难，因为选择题有4个选项。所以关于哈佛大学的校训，我即使答不对填空题，我对答对判断题还是有信心的。因为判断题难度低啊！

我们每天都要接收很多信息。是不加思考、全盘吸收，还是斟酌考量、批判继承？如果是后者，虽然会花点时间，但对事物的认识肯定更加清楚。关键是你有没有批判的意识。

问答题：简述哈佛大学的校训。

拉丁文：Amicus Plato,Amicus Aristotle,Sed Magis AmicusVERITAS.

英文：Let Plato be your friend,and Aristotle,but more let your friend be truth.

中文：与柏拉图为友，与亚里士多德为友，更要与真理为友。

哈佛大学的校徽为传统盾形，寓意坚守、捍卫；底色为哈佛标准色绯红。主体部分以三本书为背景，两本面向上，一本面向下，象征着理性与启示之间的动力关系。上面的两本书上分别刻有VE和RI两组字母，与下面一本书共同构成校训中的VERITAS，VERITAS在拉丁文中即真理。

（作者单位：华中师范大学国家数字化学习工程技术研究中心《湖北教育》编辑部）