不同流速对鲫鱼推进效率影响的数值研究

龚万阳，诸葛亦斯，刘德富

（1.三峡大学 水利与环境学院，湖北 宜昌 443002；2.中国水利水电科学研究院 水环境研究所，北京 100038）

不同流速对鲫鱼推进效率影响的数值研究

龚万阳1，诸葛亦斯2，刘德富1

（1.三峡大学 水利与环境学院，湖北 宜昌 443002；2.中国水利水电科学研究院 水环境研究所，北京 100038）

鱼类趋流性的试验和鱼类游动的数值模拟是当前研究的两个热点，大多数鱼类不仅有趋流特性而且还能高效节能的向前推进，开展鱼类趋流性与推进效率关系的研究既能完善鱼类推进机理理论，也能在鱼道设计时提高其过鱼效率。本文以鲫鱼在不同恒定流速中的实测游泳数据为依据，利用计算流体力学软件flow-3d对鱼类波状摆动进行数值模拟，建立鲫鱼游动的数值计算模型，研究在不同流速下鲫鱼完成一个运动周期后所对应的推进效率。结果表明，随着流速的增大鱼的推进效率呈现出先增大后减小的变化趋势，当流速条件为0.5m/s时对应的鱼类推进效率值最大，也是推进效率随流速变化的转折点。该研究获得了鲫鱼在顶流运动状态下鱼类推进效率与流速条件之间的相关关系。

流速；数值模拟；推进效率

1 研究背景

鱼类为适应环境在长期的自然进化过程中形成趋流行为，具体表现为鱼类感应到流速后产生相应的游泳行为，鱼类游泳行为与水力学环境的关系一直是鱼类行为学［1-2］（Fish Ethology）研究内容之一。在鱼类趋流性的研究中，目前集中于均匀流场下鱼类游泳行为与流速关系的研究，现已经取得了显著成果［3］，积累了水流因子与鱼类游泳状态以及几个关键游泳参数之间关系的研究［4-5］资料。这些研究成果大部分采用的是水槽试验法，但是由于水槽试验方法本身的局限性和测量仪器本身的限制导致某些水力学指标值不易获得。目前国内外进行生态水力学研究时通常采用数值计算的方法来获取试验仪器无法测量的水力学指标值，其中董志勇等［6］和曹庆磊等［7］通过数值计算获得了同侧和异侧竖缝鱼道模型中流速和紊动能的分布形态。但是在鱼类游泳运动方面数值模拟计算的研究成果并不多，特别是与生态学相关的研究内容更少。

采用数值模拟的方法进行鱼类游泳运动研究仅在舰船和仿生等相关领域［8］中有所涉及。Liu等［9］利用蝌蚪模型分析三维波状游动模式的水动力和推进机理，得出了鱼类波状运动与喷流推进的关系。Borazjani等［10］对鯵科运动模式进行数值模拟，结果表明水流形态对鯵科类游动的水动力性能有重要影响，丛文超［11］针对波状摆动模式进行的数值模拟，结果表明鱼体运动频率对鱼类推进性能也有影响。前人的研究局限于鱼体运动模式与鱼类推进性能的关系，缺乏不同流速中鱼类实际游泳运动节律方面的考虑。本文为探究不同恒定均匀流速环境中，鱼类游泳运动的推进效率与水流流速之间的关系，以试验实测鲫鱼运动节律为依据，建立鱼体鯵科运动模式下的二维几何运动模型来模拟在不同均匀流场中鱼体运动对水流的作用，获得相应的水力学指标值和鱼类运动指标值，采用相关的公式计算推出流速条件-鱼类运动节律-推进效率之间的关系。揭示鱼类对于不同水流流速条件的响应关系。

2 试验实测

试验以鲫鱼为研究对象，主要由于鲫鱼几乎遍布我国的各地的江河湖泊等大小水体中，鲫鱼对水流的适应性强，遇流即行，无流即止。自然界中鱼类普遍采用鯵科模式向前推进，鲫鱼的游泳方式是典型的鯵科游泳模式，而且在水槽试验中鲫鱼的游泳行为易于观测。在0.2m/s及以下流速，鲫鱼的游泳行为并不明显，而流速大于1.2m/s后，鱼的顶流时间太短，综合考虑试验条件限制以及水流流态等因素的影响，故试验流速范围定为0.3～1.2m/s。试验采用断面沿程不变的环形水槽为试验装置（见图1），电动机提供动力，带动转桨推动水流，通过调节电动机功率来调节水流流速，使得环形水槽装置试验区内的流速分别达到0.3～1.2m/s共10个固定流速。

试验过程中环形水槽中水体的日平均温度维持在20℃左右，溶解氧为7.0 mg/L左右。在每个恒定流速下进行适量的放鱼试验，共10个流速组，每组放鱼100次，每次放鱼一条。试验鱼体长为21± 2 cm，记录每个试验流速下每条鱼的运动节律，主要包括尾鳍的摆动频率、摆尾幅度和转角值。然后对每个流速组内所有鱼的运动节律统计后取平均，得到每个流速对应下鱼的运动节律值（见表1）。

图1 矩形断面环形试验装置平面图（单位：mm）

表1 不同流速下对应的鲫鱼摆尾频率、摆尾幅度和转角平均值

实际观测过程中鱼类趋流行为的具体表现形式为顶流向前，鱼通过调整身体运动姿势以某种特定的运动节奏摆动尾鳍向前推进。以往的鱼类趋流性研究中常常以鱼类游动过程中的顶流时间和趋流率作为数理统计指标，本研究以顶流过程中鱼的摆尾频率和摆尾幅度为统计指标。根据试验统计结果可知鱼类在顶流前行的过程中，不同流速条件下对应不相同的运动节律，总体上表现为随着流速条件的增大，鱼类运动的摆尾幅度和摆尾频率与流速呈现出正相关变化趋势。即水流流速越大，鱼的游泳运动越剧烈，对周围水体的作用越强。

3 数值模拟

有关研究表明鱼在游动过程中，鱼尾迹区域会出现一连串涡街，每个漩涡的转动方向恰好与卡门涡街相反，涡街产生的诱导速度的方向也与卡门涡街相反，被称为反卡门涡街。鱼在游动过程中，尾鳍上摆会在尾部下表面形成一个逆时针方向旋转的尾涡，当尾鳍摆动达到最大摆幅处，并迅速地回摆使得尾涡向后脱落出去。同上摆的过程相似，下摆时形成一个顺时针方向旋转的尾涡并在回摆时脱落出去。鱼尾反复摆动会在尾鳍后形成一连串交错排列、旋向相反的离散涡［12］，两列涡之间就形成向后的射流，产生游动的主要推进力［13］。

3.1 尾鳍运动模型建立 采用与鱼体相似的NACA0012翼型作为基本模型，各运动状态模拟形成如下：摆幅参数A的正弦规律变化实现了物理模型中鱼体尾部按实测运动规律进行摆动［14］。这样就满足了物理模型为柔性变形的要求，而且这一运动模型基本符合鱼类鯵科游泳方式［15］。其中鱼体相应的运动参数为实验实测的运动参数值，与鱼体模型中的参数符号相一致，具体输入值可见表1。

如图2所示，鱼在游动过程中，尾鳍的运动可以被分解为3个分运动的合成，沿X（负）方向的平动，沿Y方向的往复运动，以及绕Z轴的摆动。其中，沿X方向和Y方向上的运动叠加后使得尾鳍在XY平面上的轨迹为正弦曲线。尾鳍沿Y方向的平动的位移可表示为：

式中：ω为频率，rad/s；Am为鱼摆动幅度的最大绝对值。绕Z轴摆动的角位移可表示为：

式中：θmax为摆尾幅度最大的时候对应的摆尾角度；Δt为摆动落后于平动的时间。

3.2 尾鳍动力学特性分析 尾鳍在水中运动时，尾鳍对周围的水体会有力的作用，在数值模拟的过程中，flow-3d可直接返回流场值和尾鳍所受推进力，侧向力以及转矩值。由此可以计算出鱼在推进过程中有用功的大小以及总功的大小，进而推求出鱼在游泳运动过程中鱼本身推进效率的大小［16］。

从广义上讲，效率为有用功率和总功率之比，由于有用功和总功均随时间变化而变化，即推进效率可表示为：η=PX/P总，PX即为推进力功率；P总即为尾鳍的总功率，其中包括3个部分：

推进力功率：

式中：FX为推进力；UX为X方向上鱼的游泳速度。侧向力功率：

式中：FY为侧向推进力；UY为侧向平动速度。

转矩功率：

式中：T为转动力矩；θ为绕Z轴摆动的角位移。

由于在游动过程中，速度以及对应的力均在不断的变化，因而所对应的功率也随时间不断的变化，故计算时取其平均值，鱼的平均推进效率可表示为：

3.3 二维几何建模 基于鲫鱼本身的体型相对较小的特点，以及鲫鱼运动时对水体垂向上的作用相对较为均匀，可采用二维模型。对尾鳍摆动的水动力分析采用重整化群（Renormalization Group，RNG）方法，数值离散方法采用有限差分法（Finite Difference Method，FDM）流场区域为（1000×375）mm，鱼体全长210 mm，尾鳍长度63 mm，最大厚度16 mm，尾鳍两侧面呈流线型，根据鲹科鱼类尾鳍的特点［17］，转动轴位于距离后端约三分之一总长处，外围矩形边框是墙体边界，考虑到鱼在模拟计算中运动前进，本次模拟采用正方形动网格（边长为5 mm）对计算区域进行划分，共计299 980个，如图3所示。

图2 鲫鱼模型运动

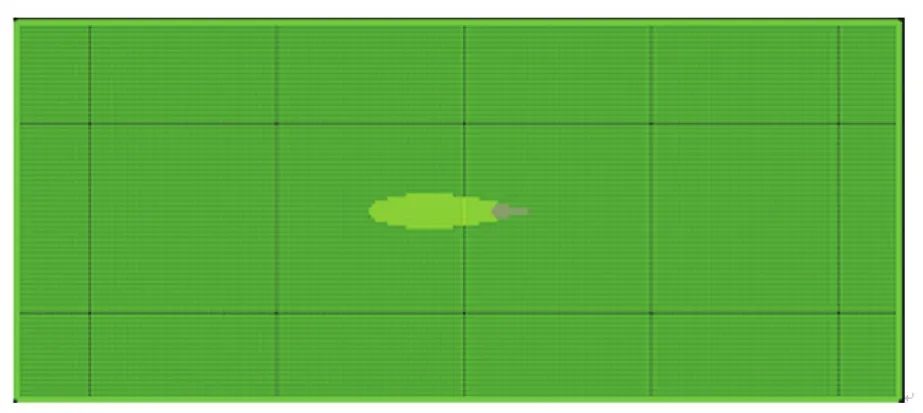
图3 鲫鱼流场建模及网格划分

3.4 控制方程和数值格式 控制方程的求解基于有限体积法，考虑黏性以及不可压缩流动，建立如下水流连续方程和水流动量方程。

水流连续方程：

水流动量方程：

式中：H=h+z，h为水头，z为水深；u、v分别表示X，Y方向的流速；Nx、Ny分别表示X、Y方向的紊黏系数；f为科氏力。

3.5 边界条件的设定及初始化 图3中，计算时鱼体表面设定为物面无滑移，流场左边界定义为流速入口（Specified velocity），右边界为出口边界（Outflow），上下边界为对称边界（Symmetry）。利用flow-3d中的动网格技术对网格进行定义，用运动控制模块选项设定尾鳍的运动参数，使得鱼体及尾鳍运动满足要求。

3.6 模型率定 实验实测可获得一个周期内鱼游泳的绝对距离值为S测，经数值模拟计算可得鱼在一个周期内鱼游泳的绝对距离值为S模。不同流速下对应的S测和S模值可见图4。S测和S模的变化趋势一致，而且不同流速对应下的S测和S模相近。说明数值模拟是准确的、鱼的运动模型是合适的。该数值模拟能够很好的反应鱼在流场中的运动情况。

图4 不同流速下对应的S测和S模值

4 数值计算结果及分析

鱼依靠尾鳍的摆动获得向前的推力克服水流阻力向前运动，流速越大对鱼向前运动造成的阻力越大，所需要的推进力也就越大。鱼通过调节自身的游泳运动状态可以获得较大的推进力，但是鱼在调节自身游泳运动状态获得较大推进力的同时侧向力也随着变大，而侧向力对鱼向前运动的作用不大，单纯的用推进力大小来表征鱼对于不同流速的相关关系并不全面，为了能够更加全面的反映流速与鱼的游泳行为关系，用推进效率来表征流速与鱼游泳运动之间的相关关系更加合适［18］。

许多学者对鱼的推进效率和鱼的游泳状态做了大量研究，并得到了鱼的推进效率和鱼的运动时间、转动攻角以及斯特哈尔数（St）之间的相关关系［16］，相应的成果也表明鱼的游泳推进效率确实与鱼的运动状态有关，通过数值模拟所获得的水力学指标值更接近试验中的实际值，根据公式计算出相应的功率，综合了推进力功率、侧向力功率和转矩功率后所得到的推进效率值，能更好的体现出鱼对于各个恒定流速的响应。

数值模拟计算中采用了与试验实测相同的流速，以及试验流速范围从0.3～1.2m/s，10个流速组中各个恒定试验流速下对应的鲫鱼摆尾频率和摆尾幅度值，在此条件下从计算软件中获取计算公式中所需的压力值和流场速度值，再根据计算公式计算出鱼运动的推进效率，计算结果见表2，根据计算结果绘制图5，流速范围为0.3～1.2m/s时，鱼的推进效率分布从总体上呈现逐渐减小的趋势，但是局部上分布表现为相对集中，流速从0.3～0.5m/s和0.6～0.9m/s，对应下的推进效率的变化幅度相对较小，当流速从1.0～1.2 m/s时，对应的推进效率变小的幅度明显，在流速为1.2 m/s时，鱼的推进效率达到最小，这一结果表明鱼在较小的流速下所需顶流前行的推力较小，然而推进效率却比较高，但是在较大的流速环境中，鱼为了克服较大的流速障碍需要较大的顶流推力，但是在获得较大推力来克服流速的同时，其推进效率往往会降低。

表2 不同流速下对应的推进效率（η）值

图5 不同流速下对应的推进效率值

鱼在不同流速环境中以不同的游泳状态向前推进，针对其推进效率与流速之间的变化关系，对推进效率值进行拟合可得推进效率关于流速的二次曲线多项式：

对拟合曲线分析可知，当流速从0.3～0.5m/s时，推进效率先缓慢变大，然后流速从0.6～0.8m/s时，推进效率随后缓慢减小，当流速大于0.8m/s后，推进效率随着流速的增加呈现出快速减小的趋势，推进效率随着流速的变化表现为鱼对流速存在某种响应关系，这种关系用拟合曲线正好能够给出定量的描述。大量的试验表明鱼对于不同流速的刺激做出的反应正好与这种变化规律相似，当流速为0.3～1.2m/s时，用推进效率来表征鱼对流速的刺激所作出的反应是合理的。

5 总结与展望

本次是以鲫鱼为试验对象，根据实测不同均匀流速组下每组鲫鱼的运动节律为依据，合理转化为数值模拟中鱼模型的运动参数值，区别于以往研究中仅仅改变其中一个或某几个变量而是以实际情况为准，数值模型能真实合理的反映鲫鱼在稳定均匀流速场中的运动情况，获得对应的压力值和流速值后，并根据公式计算推求出推进效率值。以推进效率作为鱼对流速响应的重要分析指标，当流速从0.3～0.5m/s，推进效率上升，当流速从0.6～1.2m/s，推进效率下降。推进效率总体上呈现先变大后变小的趋势。因为鱼对水体的扰动作用，水体反作用于鱼体使其产生推进力，对推进效率作关于流速的线性拟合可得二次抛物曲线，流速0.5 m/s对应的推进效率值为其规律性变化的转折点，对应的推进效率达到最大。

本文以实际放鱼试验所得资料为依据，以NACA0012翼型作为基本模型，并对鱼体运动形态进行合理的简化，经模拟获得鱼体经过一个运动周期后对水体的作用情况，根据获得的数值经计算得到鱼的推进效率值，得出鱼类推进效率对于流速呈现先增大后减小的变化规律，这一规律与鱼对流速的偏好特性相似。本次研究针对的是均匀流场条件下鲫鱼的推进效率与流速的关系，然而在天然河流、湖泊中和鱼道设施内，水流流速条件复杂多变而且不均匀，不同鱼类的推进力和推进效率也将有所不同，深入研究复杂流场环境对鱼类推进效率的影响，能进一步丰富鱼类推进机理，也能好的指导鱼道设施建设。

［1］ 何大仁，蔡厚才.鱼类行为学［M］.厦门：厦门大学出版社，1998.

［2］ 黄晓荣，庄平.鱼类行为学研究现状及其在实践中的应用［J］.淡水渔业，2002，32（6）：53-56.

［3］ Castro-Santos T.Optimal swim speeds for traversing velocity barriers：an analysis of volitional high-speed swimming behavior of migratory fishes［J］.Journal of Experimental Biology，2005，208（3）：421-432．

［4］ 宋波澜，林小涛，王伟军，等.不同流速下红鳍银鲫趋流行为与耗氧率的变化［J］.动物学报，2008，54（4）：686-694.

［5］ Merino G E，Piedrahita R H，Conklin D E.Effect of water velocity on the growth of California halibut（Paralichthys californicus）juveniles［J］.Aquaculture，2007，271：206-215.

［6］ 董志勇，冯玉平，Ervine A.同侧竖缝式鱼道水力特性及放鱼试验研究［J］.水力发电学报，2008，27（6）：126-130．

［7］ 曹庆磊，杨文俊，陈辉.异侧竖缝式鱼道水力特性试验研究［J］.河海大学学报：自然科学版，2010，38（6）：698-703．

［8］ 王亮，王明，付强.串列仿生鱼自主游动的数值模拟研究［J］.计算力学学报，2013：727-732，748.

［9］ Liu H，Kawachi K.A numerical study of undulatory swimming［J］.Journal of Computational Physics，1999，155（2）：223-247．

［10］ Borazjani Isotiropoulos F.Numerical investigation of the hydrodynamics of carangiform of swimming in the transitional and inertial flow regimes［J］.Journal of Experimental Biology，2008，211：1541-1558．

［11］ 丛文超，王志东，李力军.波状摆动式鱼类的推进性能研究［J］.中国舰船研究，2010，5（4）：1-5.

［12］ Chen Z，Doi Y.Numerical study on relaminariantion in fish-like locomotion［J］.Journal of the Society of Naval Architects of Japan，2002，191：9-16.

［13］ 焦予秦，乔志德.有侧壁干扰的机翼半模型风洞实验的N-S方程数值模拟［J］.航空学报，2001，22（2）：140-143.

［14］ 乔晓冬，焦予秦.鱼类游动的N-S方程数值模拟［J］.科学技术与工程，2007，7（8）：1536-1540.

［15］ 曹庆明.鱼类游动的水动力学研究综述［C］//第二十一届全国水动力学研讨会暨第八届全国水动力学学术会议暨两岸船舶与海洋工程水动力学研讨会.济南，2008.

［16］ 韩路辉，陈维山，刘军考，等.基于FLUENT的摆动尾鳍水动力特性研究［J］.机械设计与制造，2010（5）：204-206.

［17］ YAN Hui，SU Yu-min，YANG Liang.Experimentation of fish swimming based on tracking locomotion locus［J］. Journal of Bionic Engineering，2008，5（3）：258-263.

［18］ Hover F S，Haugsdalφ，Triantafyllou M S.Effect of angle of attack profiles in flapping foil propulsion［J］.Journal of Fluids and Structures，2004，19（1）：37-47.

Numerical study on the influence of different flow velocity on crucian propulsion efficiency

GONG Wanyang1，ZHUGE Yisi2，LIU Defu1
（1.College Hydraulic&Environmental Engineering，China Three Gorges University，Yichang 443002，China 2.China Institute of Water Resources and Hydropower Research，Beijing 100038，China）

The experiment of fish’s trend and numerical simulation of fish swimming are two hot spots in the current research.Most fish not only have the trend of the flow characteristics，but also can effectively promote energy efficiency，Carrying out fish rheotaxis and promoting efficiency of study can not only improve the fish propulsion mechanism theory，but also improve the efficiency of fish in the fishway design. Based on the measured data of crucian swimming at different constant velocity，using CFD software flow-3d to simulate the fish undulating，a numerical model of crucian swimming is established to study the efficiency of the crucian at different velocity.The results show that with the increase of the flow rate，the propulsion efficiency of fish increases firstly and then decreases；when the flow velocity is 0.5m/s，the propulsion efficiency of the fish is the maximum，and it is also the turning point of the change of the efficiency with the velocity of the flow.In this study，the relationship between the propulsion efficiency and the flow velocity of the crucian in the flow movement state was studied.

velocity；numerical simulation；propulsion efficiency

X174

A

10.13244/j.cnki.jiwhr.2016.01.001

1672-3031（2016）01-0001-06

（责任编辑：韩 昆）

2015-09-30

国家自然科学青年基金项目（51209229）

龚万阳（1990-），男，湖北宜昌人，硕士生，主要从事生态水利研究。E-mail：602915662@qq.com

诸葛亦斯（1981-）男，北京人，博士，高级工程师，主要从事生态水利研究。E-mail：zhugeys@iwhr.com