组合网格法在无压稳定渗流中的应用

张顺福，丁留谦

（1.中国水利水电科学研究院 防汛抗旱减灾研究所，北京 100038；2.水利部防洪抗旱减灾中心，北京 100038）

组合网格法在无压稳定渗流中的应用

张顺福1，2，丁留谦1，2

（1.中国水利水电科学研究院 防汛抗旱减灾研究所，北京 100038；2.水利部防洪抗旱减灾中心，北京 100038）

针对无压稳定渗流分析过程中常遇到的线形结构问题，提出将组合网格法应用于无压稳定渗流计算。采用两套独立的网格，对整体区域采用尺寸较大的粗网格进行模拟，不考虑线形结构的影响，在线形结构附近则采用尺寸比较小的细网格进行模拟，考虑线形结构的影响。计算在粗细两套网格之间迭代调整，直到达到收敛精度。组合网格法大大简化离散工作量，且适应于非规则网格。数值计算结果表明，组合网格法合理可行，计算程序可靠，这为线形结构的无压稳定渗流分析提供了一种思路和方法。

无压稳定渗流；组合网格；线形结构；改进初流量法；有限单元法

1 研究背景

在饱和无压稳定渗流有限元数值模拟中，常常会遇到这样一些结构，它们在某一方向的尺寸与整体计算区域相比非常小，比如岩体中大量存在的断层、蚀变带、软弱夹层等结构面；土石坝中常用的土工膜、防渗面板、防渗心墙、防渗帷幕等局部构造等等（为方便描述，下文中统称这些结构为线形结构或奇异区域）。当这些结构中的水流运动可以忽略不计的时候，可以采用结点双编号［1］或内部隔水边界［2］对这些结构进行处理，否则对这些结构需要进行精细离散，但这些结构在某一方向的尺寸可能达到厘米甚至毫米级别，与整体模拟区域的尺寸相差太远，根据有限元误差理论，为保持计算精度其它区域必然也需要精细的离散，从而导致离散所需结点数目和单元数目将会大大增加，且考虑到结构的空间特性，整体计算区域的离散难度将会大幅度提升，计算所需时间也大大增加，甚至到达一般计算机难以承受的程度。

对于这类局部特性强烈的线形结构，一般是采用非规则网格局部加密的方法对这些结构及其附近区域进行局部的离散加密，但局部加密网格法的要求比较高，不仅要求整个计算区域的网格质量很好，而且还要求网格的尺寸过渡非常光滑，这些条件在二维情况下尚且能够很好的满足，但在三维情况下，对复杂区域的非规则网格划分常常遇到下述问题：直接划分失败，划分成功但单元质量差，或者划分成功但单元尺寸过渡不光滑等。

为避免局部加密所遇到的问题，一种可行的方案是采用非拟一致网格（Non-conform ing Grid）技术，非拟一致网格技术的主要思想是将整体区域分解为相互之间只在区域表面有交集的不重叠小区域，区域采用独立的网格离散，区域之间不需要满足网格协调的要求，区域之间的连续性条件通过多点约束技术（Multiple-Point Constraints）实现，通过运用这种局部区域协调、整体区域非协调的网格离散方式，达到不同的局部区域上采用不同的网格离散或者不同的数值计算方法的目的，也就是说可以在某个区域采用有限元方法进行计算，而在其它区域采用有限体积或者有限差分进行计算［3］。

非拟一致网格技术很好的将局部特性控制在小范围内，使局部区域的特性不至于导致整体计算的急剧增长。但有效的适应局部特性目标往往与计算求解过程相冲突，包括：（1）由于离散尺寸的差异变化而导致方程求解器会降低效率甚至求解失败；（2）由于考虑了非结构网格，数据结构变得繁琐；（3）计算机体系结构可能会不能够高效的处理非规则网格的影响（比如，向量化被抑制）；（4）即使是在离散过程中，这个目标也会带来重重困难，对于有限差分格式而言，很难为非规则网格构造出相应的高精度差分格式；对于有限元计算而言，一组质量好的非结构化网格的自动生成意味着高额的花销［4-6］。

为避免非拟一致网格的困境，Mc Cormick［6］提出了一种有叠加的区域分解法——快速自适应组合网格（FAC）方法。FAC方法首先形成一套对应于整体区域的规则粗网格，然后对规则粗网格上相应于关注的局部区域形成一套或者多套与整体粗网格嵌套的细网格，计算的时候先对粗网格求解，然后将粗网格的计算结果通过延拓算子延伸到细网格上，进而获得细网格上的误差，将这些误差再通过限定算子返回粗网格上，粗细网格之间循环迭代，反复对误差进行校正直至收敛［7-8］。

由于规则网的处理（离散与求解）相对不规则网而言要容易得多，从而使得快速自适应组合网格（FAC）方法成为非常有效的方法，但是快速自适应组合网格（FAC）方法高效性有2个基本要求：（1）“嵌套”和“结构化或规则的网格”又往往成为其应用的限制条件，由于工程实际问题中区域的复杂性使得规则网格和“嵌套”的规则网格往往很难甚至无法得到；（2）FAC方法相关的数值计算格式以“嵌套”为基础，如果不满足“嵌套”条件，那么几乎所有相关的计算都无从下手。这些均使得FAC的应用收到了限制。

为此，本文引入一种改进的快速自适应组合网格法——组合网格法（Composite Grid Method，CGM）。CGM继承了FAC反复在粗细两套网格进行误差校正的思想，并且可以使用非规则网格，细网格和粗网格相互独立，不要求网格嵌套组合网络法，该方法已广泛应用于水工结构［9］、油田开采数值模拟［10-11］、电磁场［12］、电磁-机械耦合［13］、焊接数值模拟［14-16］等领域。

2 无压稳定渗流基本理论

根据微分体质量守恒定律，在渗流区域D，三维地下水稳定渗流微分方程为［17］：

式中：xi为笛卡尔直角坐标系的坐标轴；vi为沿坐标轴xi方向的渗流速度，m/s；W为源或汇项，1/s，以获得水流为正。

同时满足Darcy定律：

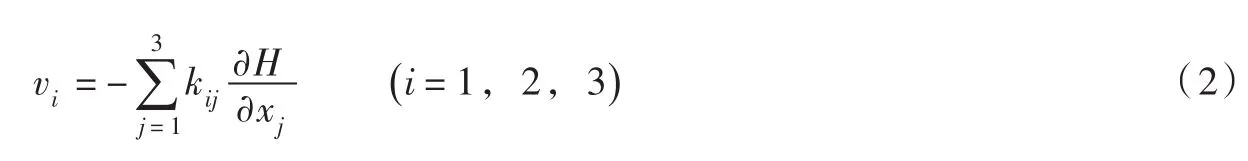
式中：kij为渗透系数；H为总水头，m，；p为孔隙水压强，Pa；γ为水的容重，N/m3。定解条件如下（如图1所示）。

（1）定水头边界Γ1：

（2）流量边界Γ2（以流入为正）：

（3）自由面边界Γ3：

图1 渗流计算边界条件

（4）渗流逸出边界Γ4：

式中：H0为已知水头函数，m；q为已知流量，m3/s；ni为边界外法线方向余弦。

无压稳定渗流控制方程属于椭圆型偏微分方程，本文采用基于子域积分改进的初流量法［18］进行求解。

3 组合网格法原理

3.1 组合网格法基本思想 组合网格法是一种有叠加的区域分解算法，其基本思想是：采用粗网格和细网格两套网格进行分析计算，粗网格对应整个区域，不考虑线形结构的影响，细网格则为包含线形结构在内的局部区域。两套网格之间反复迭代直至收敛，网格之间的信息交互通过网格空间位置插值实现，网格之间无需嵌套，因此适应性强，规则网格和非规则网格均可使用［19］。组合网格法是文献［20-21］所提出的方法的改进从数学上证明了用两套网格所求得的数值解可以在粗网格区域达到粗网格的精度，在细网格区域达到细网格的精度，从理论上证明了组合网格法的有效性。

图2 计算区域

式中：u、v分别为细网格区域未知量及细网格以外区域的水头值；为相应区域的偏微分算子；为初始流速［22］，Wp为相应区域的源或汇项；Γ=Ωc⋂Ωf为两个区域的交界的边界。

采用尺寸比较大的粗网格TH对整体区域Ω进行网格剖分，得到有限元离散空间SH；采用尺寸比较小的细网格Th对区域Ωf也进行网格剖分，得到有限元离散空间Sh。

根据虚位移原理，式（7）对应的虚功方程为：

推导得到边界Γ上满足［19］:

3.3 程序编制 组合网格算法在三维稳定无压渗流计算中实现的具体流程如图3［25］所示，其中a场代表粗网格区域，b场代表采用细网格控制参数的细网格区域，c场代表采用粗网格控制参数的细网格区域，Uf、Uc分别为b场和c场的水头值。据此编制了相应的三维有限元程序IIFM3DS-CGM［25］。

某无限长土坝宽100.5m、高30.0m，中部有0.5 m的垂直心墙，心墙距离上游50.0 m，如图4所示。心墙和坝壳均为各向同性材料，上游水位为30.0m，下游水位为6.0m。坝长方向取单位长度，采用组合网格法，用细网格模拟心墙及其上、下游17.0 m区域范围，整体区域则用粗网格进行离散，其中细网格心墙处的六面体单元尺寸为0.125m×1m×0.25m，心墙上、下游2m范围内单元尺寸为0.25m×1m×0.25m，其它区域单元尺寸为1m×1m×0.25m，如图5。粗网格不考虑心墙的影响，单元尺寸大小0.995m×1m×1m，如图6。为验证组合网格法的精度，文中同时采用较细的网格对整体区域进行离散，整体细网格在心墙及其上、下游17 m的范围内采用与图6一样的网格剖分，其它区域用尺寸为1m×1m×0.25m的单元进行离散。

表1给出了坝壳渗透系数k1与心墙渗透系数k2不同比值下，组合网格法计算得到的心墙下游出水

图3 计算流程

4 算例

图4 计算模型

图5 不考虑心墙的整体区域及相应粗网格剖分（组合网格法）

图6 考虑心墙的局部区域及相应细网格剖分（组合网格法）

表1 心墙下游出水点高程比较

点高程与整体区域细网格的计算结果比较，从表1可以看到，组合网格法计算的结果与整体区域细网格的计算结果基本一致，最大误差为2.3%。图7给出了不同渗透系数比值条件下，组合网格法计算得到的心墙附近自由面与整体区域细网格计算结果的比较。从图7可以看到，组合网格法的计算结果与整体区域细网格的结果非常接近。

5 结语

无压稳定渗流有限元分析中，线形结构增加了计算区域的离散难度。本文介绍了组合网格法的基本原理，并将其引入到稳定无压渗流有限元分析中，为线形结构的模拟提供了一种新思路。

图7 组合网格与整体细网格的自由面比较

由于组合网格的粗、细网格可以独立生成，因此组合网格法对线形结构的网格剖分具有较强的适应性，能极大的简化无压渗流计算的网格剖分工作。组合网格法在粗网格区域达到粗网格的精度，在细网格区域达到细网格的精度。

结合改进的初流量法给出了稳定无压渗流组合网格算法格式和计算流程，并编制了相应的三维有限元程序IIFM3DS-CGM。采用垂直心墙算例对算法和程序进行了验证，结果证明算法是合理的，程序是有效的、可信的。

本文的研究成果还需结合实际工程进行更深入的研究。

［1］ 王浩然，朱国荣 .淄博市孝妇河源区地下水资源的开发利用研究［J］.高校地质学报，2000，4（2）：198-204.

［2］ 薛禹群，谢春红.水文地质学的数值法［M］.北京：煤炭工业出版社，1980.

［3］ Bernardi C，Maday Y，Patera A.Domain decomposition by the mortar finite element method［J］.Asymptotic and Numerical Methods for PDEs with Critical Parameters，1993，384：269-286.

［4］ Mc Cormick S，Thomas J.The fast adaptive composite grid（FAC）method for elliptic equations［J］.Mathematics of Computation，1986，46：439-456.

［5］ 吕涛，石济民，林振宝.区域分解算法［M］.北京：科学出版社，1992.

［6］ Mc Cormick S.Fast adaptive composite grid（FAC）methods：theory for the variational case［J］.Defect Correction Methods Computing Supplementum，1984，5：115-121.

［7］ 江思珉，朱国荣，王浩然，等 .FAC方法在地下水数值模拟中的应用［J］.水利学报，2006，37（11）：1389-1392.

［8］ 陶文铨.数值传热学［M］.第2版.西安：西安交通大学出版社，2001.

［9］ 郭胜山，李德玉，唐菊珍.水工结构动接触问题的组合网格算法［J］.水力发电，2009（5）：24-26.

［10］ 韩修廷，梁国平，吴恩成，等.油田套管损坏数值模拟专用软件开发及应用［J］.数字石油和化工，2006（4）：33-36.

［11］ 王伯军，张士诚，张劲，等.考虑注采关系的三维地应力场数值模拟研究［J］.西南石油大学学报：自然科学版，2006（6）：33-35.

［12］ 甘艳，阮江军，张宇，等.组合网格法及其在电磁问题中的应用［J］.电工技术学报，2008，23（8）：8-14.

［13］ 张宇，阮江军，刘兵，等.组合网格法在电磁-机械耦合问题中的应用［J］.中国电机工程学报，2007，27（37）：42-47.

［14］ 陈文平.组合网格法及其在焊接数值模拟中的应用［D］.福州：福建师范大学，2009.

［15］ 陈文平，马昌凤，蒋利华.组合网格法在搅拌摩擦焊接数值模拟中的应用［J］.安徽理工大学学报：自然科学版，2009（2）：57-61.

［16］ 陈文平，马昌凤，蒋利华.激光焊接问题的组合网格法［J］.福建师范大学学报：自然科学版，2009（3）：29-32

［17］ 王洪涛.多孔介质污染物迁移动力学［M］.北京：高等教育出版社，2008.

［18］ 张顺福，丁留谦，刘昌军，等.基于子域积分的初流量法改进［J］.水电能源科学，2013，31（3）：15-18.

［19］ 王德生.组合网格法和非结构化网格自动生成［D］.北京：中国科学院数学研究所，2001.

［20］ Xu J.Iterative Methods by Space Decomposition and Subspace Correction［J］.SIAM Review，1992，34（4）：581-613

［21］ Xu J.The auxiliary space method and optimal multigrid preconditioning techniques for unstructured grids［J］. Computing，1996，56（3）：215-236.

［22］ 张有天，陈平，王镭.有自由面渗流分析的初流量法［J］.水利学报，1988（8）：18-26.

［23］ 李新强.无压渗流有限元分析的改进初流量法［J］.水利学报，2007，38（8）：961-965.

［24］ 王媛.求解有自由面渗流问题的初流量法的改进［J］.水利学报，1998（3）：68-74.

［25］ 张顺福.子域积分法及组合网格法在无压渗流中的应用［D］.北京：中国水利水电科学研究院，2013.

Application of composite grid method in unconfined seepage analysis

ZHANG Shunfu1，2，DING Liuqian1，2

（1.China Institute of Water Resources and Hydro Power Research，Beijing 100038，China；2.Research Center on Flood&Drought Disaster Reduction of the Ministry of Water Resources，Beijing 100038，China）

To solve the“line-style structure”problem often encountered in unconfined steady seepage analysis，Composite Grid Method is adopted.Two sets of independent grids are used in numerical simulation. One is the coarse grid of larger size simulating the entire region without consideration of“line-style structure”and the other is the fine grid of relatively small size simulating the domain including the“line-style structure”.Adjustments are carried out iteratively between the coarse grid and fine grid until desired convergence precision is achieved.With Composite Grid Method，the amount of discretization is greatly reduced. The Composite Grid Method can be adapted to non-regular grid.Numerical simulation result shows that the theory is reasonable and the program is reliable.Composite Grid Method provides an approach to solving the“line-style structure”problem in unconfined steady seepage analysis.

unconfined steady seepage；Composite Grid Method；line-style structure；improved Initial Flow method；Finite element method

TV139.14

A

10.13244/j.cnki.jiwhr.2016.01.003

1672-3031（2016）01-0016-07

（责任编辑：李 琳）

2015-08-04

中国科技部国际合作项目（2010DFA74520）

张顺福（1982-），男，广西人，博士，工程师，主要从事渗流与控制研究。E-mail：zhangshunfu@live.cn