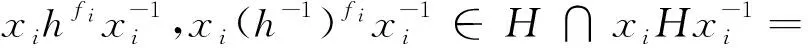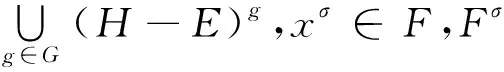广义转移的应用(Ⅱ)*
刘 秀,韦华全,韩 艳
(1.昭通学院 数学与统计学院,云南 昭通 657000;2.广西大学 数学与信息科学学院,广西 南宁 530004)
广义转移的应用(Ⅱ)*
刘 秀1,韦华全2,韩 艳1
(1.昭通学院 数学与统计学院,云南 昭通 657000;2.广西大学 数学与信息科学学院,广西 南宁 530004)
利用已有的广义转移映射的概念和性质研究其对有限群结构的影响.首先考察G到Z(G)内的广义转移VG→Z(G),证明了G′的阶有限;然后考察G到可解子群H内的广义转移VG→H,证明了F为G的正规子群且G=FH及F∩H=E,即G为群F被群H的扩张;最后设G是p-正规的,考察G到其Sylow p-子群P内的广义转移VG→P,利用已推广的Grün第一定理,推广了Grün第二定理.这些结果的获得使有限群的自同构群研究方法、子群嵌入研究方法得到新的发展,局部分析方法也得到新的应用.
有限群;广义转移;Grün第二定理
有限群的研究大致可以分为有限群的构造和有限群表示.研究有限群的构造,有以下几个最重要的研究方向:有限单群的同构分类,有限群的自同构群,有限群的扩张问题,有限可解群理论,子群特性对有限群结构的影响等.这些课题一直是有限群研究的活跃课题.有限单群的同构分类已于20世纪80年代得到解决,而其余的研究方向就自然成为人们研究的主要课题.
确定一个已知群的非单性或可解性,是群论中最重要的课题之一,其中转移方法是行之有效的研究方法.转移方法考察群G到它的一个子群H的可换商群H/H′的同态,其作用是确定G的可换(或稍加推广为可解)商群的存在性.迄今为止,人们对于H为G的p-西洛子群的情况作了较深入的研究.在p-西洛子群内的转移给出G的极大可换p-商群.我们还知道,只要对G的p-西洛子群P的结构给予一定限制,那么G的极大可换p-商群便同构于NG(P)的极大可换p-商群.例如,若P是交换的,则上述结论成立(见Burnside定理[1]).若考虑P在G中的嵌入,例如,P与其在G中的共轭的交的情况便得到Grün定理[2].
在群的映射中,反同态映射是与同态映射相对应的,它们是互为对称的映射.在现实世界中,对称的事物也比比皆是,而对称的美正是正反双方的统一,因此,我们希望能用统一的思想处理群的同态映射和反同态映射.为此,我们引入了广义同态映射的概念,并利用这一概念,研究了有限群的广义自同构群、群在群上、群在集合的广义作用、有限群的广义特征子群、有限群的广义扩张、算子群等,能以统一的观点处理若干相关的结果[3-13].
基于同样的统一的思想方法,我们引入广义转移映射的概念,得到了广义的初步性质,并应用它推广了p-幂零群的一个充分条件——Burnside定理[14].我们还研究了广义转移的应用,推广了Grün第一定理[15].笔者进一步研究广义转移的应用,证明了几个较为深刻的结果,推广了Grün第二定理.
1 预备知识
定义1[4,16]设G1,G2是群,映射f:G1→G2叫做G1到G2的广义同态映射,如果∀a,b∈G1,等式(ab)f=afbf和(ab)f=bfaf至少有一个成立.
定义2[14]所谓G到H内的广义转移指的是G到H/H′内的映射VG→H,满足
定义3[17]设G是有限群,P是G的Sylow p-子群,如果对任意的g∈G,若
Z(P)g≤P,则Z(P)g=Z(P),我们称G是p-正规的.
引理1[18]设G=
引理2[14]VG→H是G到H/H′内的广义同态.
引理3[4]设f是群G1到群G2的反同态满射,H◁G1且H⊆Ker f,则存在唯一的G1/H到G2的反同态满射f*,使得f=φf*,这里φ是G1到G1/H的自然同态满射.当且仅当Ker f=H时,f*是G1/H到G2的反同构映射.
引理4[1]G′是G的全不变子群,并且若N◁G,则G/N是交换群⟺N≥G′.
引理5[15]设H 引理6[14]若|G:H|有限,g∈G. 引理7[15]设G是有限群,P是G的Sylow p-子群,则有 引理8[15]设G是有限群,P是G的Sylow p-子群,则 P∩G′= 定理1 设G为一群,未必是有限的,但 |G/Z(G)|<∞,则|G′|<∞. 证明:由于G′/(G′∩Z(G))≅G′Z(G)/Z(G)≤G/Z(G),故 |G′/(G′∩Z(G))|<∞. G′=<[ri,rj]|i,j=1,…,n>, 定理2 设H为G的可解子群能使H∩Ht=E,对一切t∈G-H.则集合 为G的正规子群且成立G=FH及F∩H=E. 证明:若H=E,则有F=G,结论显然成立.故以下假定H≠E. 1)先证明F为G的子群. 考虑G到H内的广义转移VG→H并证明: a)对∀h∈H均成立V(h)=hH′;特别地对于K=KerV成立H∩K=H′: 由引理6得 因为i=1时的轮换为(Hx1,Hx1h,…,Hx1hfi),由h∈H便有Hx1h=Hh=H,故f1=1.若i>1,则由假定 从而V(h)=hH′或V(h)=h-1H′. 对∀h′∈H′,则h′∈H,且V(h′)=h′H′=H′或V(h′)=(h′)-1H′=H′, 所以h′∈K,得h′∈H∩K.对∀h∈H∩K,则h∈H,K,于是V(h)=hH′=H′或V(h)=h-1H′=H′,所以h∈H′.所以得到H∩K=H′. b)成立G=KH: 设g∈G,则有h∈H能使V(g)=hH′.由a),V(h)=hH′或V(h)=h-1H′. 故V(gh-1)=H′或V(gh)=H′,从而gh-1∈Ker V=K或gh∈Ker V=K,于是g∈Kh≤KH或g∈Kh-1≤KH,由此得G≤KH.所以G=KH. c)由K∩H=H′及H≠E的可解性可知K H′∩H′k≤H∩Hk=E. 由归纳假定,可假设对于K定理已得证.即 为K的正规子群并能使K=NH′,N∩H′=E且 |N|=|K∶H′|.对于g=hk∈HK=G成立 N∩Hg=N∩Hk=N∩(K∩Hk)=N∩H′k=E. 但又有 |N|=|K∶H′|=|K∶K∩H|= |KH∶H|=|G∶H|=|F| 故N=F.即F为G的子群. 2)证明F◁G. 3)证明G=FH及F∩H=E. 由F的定义可得F∩H=E. 若t′t-1∈G-H,则H∩Ht′t-1=E,于是有 Ht∩Ht′=E.从而 |F|=|G|-|G∶H|(|H|-1)=|G∶H|.由于F∩H=E及F≤G,即得|FH|=|F||H| =|G|,故得G=FH. 定理3 设G是p-正规的有限群,P是G的Sylow p-子群,则 G/G′(p)≅NG(Z(P))/NG(Z(P))′(p). 证明:由于Z(P)char P,故P≤NG(Z(P)),于是P是NG(Z(P))的Sylow p-子群.由引理7有 G/G′(p)≅P/(P∩G′). 将引理7用于NG(Z(P))得出 NG(Z(P))/NG(Z(P))′(p)≅P/(P∩ NG(Z(P))′) 显然只需证明P∩G′=P∩NG(Z(P))′. 显然有P∩NG(Z(P))′≤P∩G′. 故仅需证明 P∩G′≤P∩NG(Z(P))′. 由引理8,有P∩G′= 由于NG(P)≤NG(Z(P)),显然有 P∩NG(P)′≤P∩NG(Z(P))′. 现在证明 P∩P′g≤P∩NG(Z(P))′. 设T=P∩P′g.显然有Z(P)≤NG(T).又因Z(P)g是Pg的中心,故Z(P)g≤NG(T),从而存在NG(T)的Sylow p-子群P1,P2能使Z(P)≤P1,Z(P)g≤P2. 由G的p-正规性即得Z(P)=Z(P*)=Z(P)gs,故gs∈NG(Z(P)). 由s∈NG(T)得 T=Ts=Ps∩P′gs. 由于P≤NG(Z(P)),又得 P′gs≤NG(Z(P))′gs≤NG(Z(P))′ 故 T=P∩P′g=Ps∩P′gs≤P∩NG(Z(P))′. [1]徐明曜.有限群导引(上册)[M].北京:科学出版社,1999. [2] B.胡佩特.有限群论(第一卷第二分册)[M].福建:福建人民出版社,1992. [3]刘秀,韦华全,黄杰山.有关广义自同构群的一些结论[J].广西师范学院学报:自然科学版,2007,24(3):1-4. [4]韦华全,刘秀,杨丽英.广义自同构与有限群结构[J].四川师范大学学报:自然科学版,2008,31(5):522-525. [5]刘秀,韦华全,谷伟平,等.广义作用与有限群结构[J].广西师范学院学报:自然科学版,2009,26(2):1-4. [6]韦华全,刘秀,黄杰山.广义同态与算子群[J].大学数学,2010,26(4):85-89. [7]刘秀,郭龙先,韦华全.算子群与直积分解[J].广西科学,2011,18(1):1-4. [8]刘秀,张建元,韦华全.有限群的广义特征子群[J].广西师范学院学报:自然科学版,2011,28(1):4-6. [9]刘秀,韦华全,杨惠娟.广义特征子群的某些判定与广义作用[J].内蒙古师范大学学报:自然科学版,2013,42(5):515-517. [10]刘秀,韦华全,董延寿.群的广义全不变子群的某些判定[J].太原师范学院学报:自然科学版,2013,12(2):13-15. [11]刘秀,韦华全.有限群的广义扩张[J].广西师范学院学报:自然科学版,2013,30(2):12-15. [12]刘秀,韦华全.有限群的广义扩张Ⅱ[J].广西民族大学学报:自然科学版,2013,19(2):37-39. [13]刘秀,韦华全.群在集合上的广义作用与有限群结构[J].佳木斯大学学报:自然科学版,2013,31(6):621-623. [14]刘秀,韦华全,马儇龙.有限群的广义转移[J].云南民族大学学报:自然科学版,2014,23(1):48-51. [15]刘秀,马儇龙,韦华全.广义转移的应用[J].宁夏师范学院学报:自然科学版,2013,34(6):47-50. [16]班桂宁.关于群的弱同态[J].江西师范大学学报:自然科学版,1998,22 (3):201-204. [17]徐明曜.有限群导引(下册)[M].北京:科学出版社,1999. [18] B.胡佩特.有限群论(第一卷第一分册)[M].福建:福建人民出版社,1992. [责任编辑 苏 琴] [责任校对 黄招扬] The Further Application of the Generalized Transfer LIU Xiu1,WEI Hua-quan2,HAN Yan1 (1.SchoolofMathematicsandStatistics,ZhaotongUniversity,Zhaotong657000,China; 2.CollegeofMathematicsandInformationScience,GuangxiUniversity,Nanning530004,China) By using the concept and property of generalized transfer we have to study its effect on the structure of finite groups.Firstly,the result thatis a finite group is proved when we made the generalized transfer mapping from to.Then,the conclusion ofis a normal subgroup of and,,which also said thatis an extension of by is obtained when we used the generalized transfer mappingfromto solvable group.Finally ,letis anormal group ,the second theory of Grün has been generalized when we studied the generalized transfer mappingfromto Sylowsubgroupand used the the first theory of Grün which had been generalized.These results attained will make the research methods of automorphism group and subgroup embedding to get new development,meanwhile local analysis method can also obtain new application. finite group;generalized transfer;the second theory of Grün 2016-03-20. 国家自然科学基金(11361006);云南省教育厅科学研究基金(2014Y500);云南省应用基础研究计划项目(2016FD082). 刘秀(1980-),女,广西玉林人,硕士,昭通学院数学与统计学院讲师,研究方向:有限群论. O152.1 A 1673-8462(2016)03-0055-04
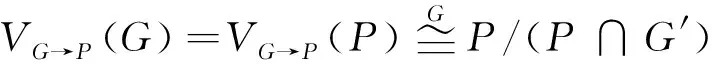
2 主要结果